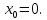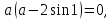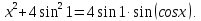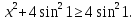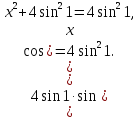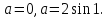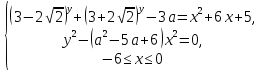Симметрия в задачах с параметром
Существует множество задач с параметром, в которых задание ставится следующим образом: «Найдите все значения параметра, при которых уравнение имеет единственное решение». Главным словом здесь будет «единственное». Стоит обратить внимание, что в таких задачах очень часто уравнение не меняется при замене знака одной или нескольких переменных, или при перестановке переменных местами. Этим необходимо пользоваться. Разберем на примерах:
Найдите все значения параметра \(b\), при которых уравнение \(-4x^2+b*cos(sinx )-2b^2\)=0 имеет единственное решение.
Пусть \(
Итак, при \(x=0\) наше уравнение принимает вид \(b-2b^2=0\) ⇔ \(b=0;\) \(b=2;\) Мы нашли значения параметра, при которых у нас возможно единственное решение. Но еще нужно проверить, а будет ли при этих значениях параметра решение единственным. Просто подставим в исходное уравнение.
При \(b=0\) получаем: \(-4x^2=0\) ⇔ \(x=0\) – решение единственное.
$$ -4x^2+2 cos(sinx )-8= 0,$$ $$ 4x^2+8=2cos(sin(x)).$$
Левая часть данного уравнения больше 8, а так как область значения \(cos(x ∈[-1;1])\), то максимальное значение правой части равно 2. Получившееся уравнение не будет иметь корней. При \(b=2\) корней нет.
Найдите все значения параметра \(a\), при которых система
имеет единственное решение.
Заметим интересную особенность:
Наша система симметрична относительно переменной \(y\). А значит, если \((
Решив систему, найдем значения параметра \(a\):
Проверим каждое значение параметра, подставив в условие задачи.
При \(a=-1\) наша исходная система имеет вид:
Попробуем оценить первое уравнение. Напомним, что сумма двух взаимно обратных величин всегда больше равна 2: \((3-2\sqrt<2>)^y+(3+2\sqrt<2>)^y≥2. \)
\(x^2+6x+2≤2\), при \(-6≤x≤0\). (см. рис. 20)
Задача 18: метод симметричных корней
Очень часто в задаче C5 требуется найти такие значения параметра a , при которых уравнение или неравенство имеет строго один корень. И если вам попалась такая задача, но вы смотрите на уравнение и не понимаете, как к нему подступиться, то вполне возможно, что вам поможет метод, изложенный в этом видеоуроке.
В двух словах: уравнение может быть специально составлено таким образом, чтобы корни были симметричными. Например, если x 1 = 5 является корнем, то и противоположное ему значение x 2 — тоже корень. Таким образом, корни всегда идут парами, как бы симметрично относительно нуля. И лишь в одном случае у корня не будет пары: когда x 1 = 0.
Таким образом, если вам удастся доказать, что единственный допустимый корень — это ноль (ну, или любое другое число — зависит от задачи), то исходная формула упрощается на порядок, и вам остается решить обычное уравнение относительно параметра. Взгляните на видео:
А теперь попробуйте решить аналогичные задачи самостоятельно. Будьте осторожны: это настоящие C5 из ЕГЭ по математике! Впрочем, теперь, когда вы все знаете, эти задачи не представляют для вас сложности.:)
Симметрия в задачах с параметром
Рассмотрены задачи с параметром, имеющие «симметрию» относительно знака или «симметрию» относительно перестановки переменных. Материал полезен при подготовке к ЕГЭ по математике.
Просмотр содержимого документа
«Симметрия в задачах с параметром»
«Симметрия» в задачах с параметром
Определенную группу задач с параметром составляют задачи, в формулировке которых ключевым является слово «единственное». В этих задачах требуется найти все значения параметра, при которых уравнение (неравенство, система) имеет единственное решение. Эти задачи имеют особенность: их условия не изменяются при замене знака одной или нескольких переменных («симметрия» относительно знака) или при перестановке нескольких переменных («симметрия» относительно перестановки переменных). Эта особенность – ключ к решению задачи.
Найти все значения параметра a, при которых уравнение
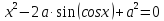
Если число x0 является решением данного уравнения, то и число 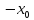
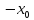
При 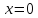
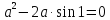
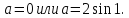
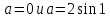
Пусть 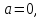
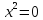
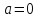
Пусть 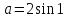
Оценим обе части полученного уравнения. Так как 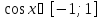
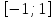
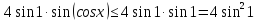
Левая часть
Поэтому уравнение 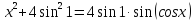
Единственным решением этой системы является х = 0. Значит, 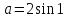
Ответ:
Найти все значения параметра 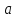
имеет единственное решение.
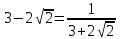
Поэтому, если пара является решением исходной системы, то и пара также является ее решением. Значит, для того чтобы решение было единственным, необходимо равенство , то есть При y = 0 исходная система примет вид:
Решая второе уравнение системы, имеем:
или 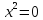
Подставим х = 0 в первое уравнение:
Итак, допустимые значения параметра:
Проверим, какие из этих допустимых значений удовлетворяют условию задачи.
При исходная система примет вид:
Оценим обе части первого уравнения системы. как сумма взаимно обратных положительных величин.
Поэтому последняя система равносильна следующей:
Значит, при исходная система имеет единственное решение (0; 0).
Пусть . Тогда исходная система примет вид:
Следовательно, при система имеет единственное решение (-3; 0).
При исходная система примет вид:
Система не имеет решения.
Найти значения параметра t, при которых система имеет два решения.
Если – решение системы, то , также будут решениями системы. Два решения будут в случае или .
При x = y исходная система примет вид: Из уравнения найдем допустимые значения параметра t: t = 1; t = 3.
При исходная система примет вид: Из уравнения
найдем допустимые значения параметра t: t = 1; t = 3.
При t = 1 исходная система примет вид: Система не имеет решения при t = 1. Значение t = 1 не удовлетворяет условию задачи.
При t = 3 исходная система примет вид: Прибавим к первому уравнению системы второе уравнение, умноженное на 2. Затем вычтем из первого уравнения второе уравнение, умноженное на 2.
Система примет вид: или
При t = 3 исходная система имеет два решения:
При t = 3 исходная система примет вид: Система не имеет решений при t = 3. Значит, t = 3 не удовлетворяет условию задачи.
При t = 1 исходная система примет вид:
При t = 1 система (исходная) имеет два решения:
Найти значения параметра 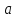
Пусть решение системы, тогда также решение системы.
Система будет иметь единственное решение при , то есть
При 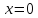
При 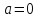
или или три решения.
Значит, 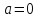
При исходная система примет вид: Из первого уравнения системы , из второго уравнения Следовательно, , тогда Система имеет единственное решение (0; 1).
При каких значениях параметра 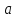
Если решение данного уравнения, то и также является его решением в силу четности функции в левой части уравнения. Следовательно,
При 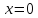
Проверка. При 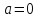
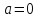
При исходное уравнение примет вид: Левая часть уравнения правая Следовательно, решением уравнения является решение системы: х=0 – единственное решение.
Найти значения параметра при которых система имеет два решения.
Если – решение данной системы, то , также являются решениями этой системы. Два решения будут, если или .
При x = y система примет вид:
Допустимое значение параметра 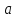
При система примет вид: и не имеет решения.
Проверка: при 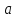
Ответ: 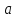
Найти все значения параметра при каждом из которых уравнение имеет единственный корень.
Уравнение не изменится, если заменить числом . Следовательно, уравнение имеет четное число ненулевых решений, а нечетное число решений будет только тогда, когда одно из них 0.
Подставим 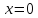
Если , то исходное уравнение примет вид:
Значит, исходное уравнение имеет три решения: -2; 0; 2.
http://www.berdov.com/ege/parametr/metod-simmetrichnih-kornei/
http://multiurok.ru/index.php/files/simmetriia-v-zadachakh-s-parametrom.html