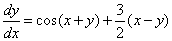Simulink решение системы линейных уравнений

Решение СЛАУ и матрицы в Matlab

Доброго времени суток, читатели! Сегодня мы поговорим о матрицах в Matlab, об их применении в решении систем линейных алгебраических уравнений. Подробно разберем методы решения, и для этого необходимо знание нескольких базовых алгоритмов.

Также стоит отметить, что у каждого алгоритма, которым мы будем искать решение СЛАУ в Matlab, своя скорость нахождения этого решения, наличие или отсутствие условия выполнения алгоритма и т.д.

В традициях нашего сайта разберём на примере:

Решить систему линейных уравнений:

4*a + b — c = 6
a — b + c = 4
2*a — 3*b — 3*c = 4

Метод обратной матрицы в Matlab

Начнем с достаточно распространенного метода. Его суть состоит в том, что сначала необходимо выписать коэффициенты при a, b и c (то есть те коэффициенты, которые находятся слева) в одну матрицу, а свободный член (то есть то, что справа) в другую.

В итоге у нас получится 2 матрицы:

Для реализации этого метода (и следующих методов тоже) требуется одно условие: чтобы определитель матрицы, составленной из коэффициентов левой части не был равен нулю. Проверка на определитель:

После проверки условия можем перейти к следующему шагу: нахождение обратной матрицы. В Matlab для этого используется оператор inv .
А само решение СЛАУ в Matlab находится как перемножение найденной обратной матрицы на матрицу свободных членов:

Мы получили 3 значения, которые и соответствуют нашим коэффициентам: то есть a = 2, b = -1, c = 1 . Можете проверить, подставив полученные ответы в исходную систему, и убедиться, что мы решили СЛАУ правильно.

Также следует отметить, что матрицы нужно перемножать именно, как сделали мы, то есть слева обратная матрица, справа матрица свободных членов.

Если вы не все поняли, то советую вам почитать нашу статью по основам Matlab.

Метод Гаусса

Метод Гаусса в Matlab реализуется достаточно просто: для этого нам нужно всего лишь изучить один новый оператор.
(\) — левое деление.
При следующей записи:

Мы получим ответы на нашу исходную систему. Только заметьте, мы решили СЛАУ стандартным набором функций в Matlab, и желательно этот оператор использовать когда матрица коэффициентов квадратная, так как оператор приводит эту матрицу к треугольному виду. В других случаях могут возникнуть ошибки.

Метод разложения матрицы

Теперь поговорим о разложении матрицы. Нахождение решения через разложение матрицы очень эффективно. Эффективность обусловлена скоростью нахождения решения для данного вида систем и точностью полученных результатов.

Возможны следующие разложения:

• разложение Холецкого
• LU разложение
• QR разложение

Разберём решение через LU и QR разложение, так как в задачах чаще всего встречается задание на решение именно через такие разложения.

Основное отличие этих двух разложений: LU разложение применимо только для квадратных матриц, QR — возможно и для прямоугольных.

LU разложение

Решим выше предложенную задачу через LU разложение:

QR разложение

И через QR разложение соответственно:

Отметим, что апостроф ( ‘ ) после Q означает транспонирование.

Стандартные функции Matlab

Так же Matlab предлагает функцию linsolve , с помощью которой возможно решить систему линейных алгебраических уравнений. Выглядит это так:

Как видите, ничего сложного тут нет, на то они и стандартные функции Matlab.

Повторение

Итак, сегодня мы с вами изучили несколько методов для решения СЛАУ в Matlab, как с помощью матриц, так и с помощью стандартных функций. Давайте их повторим на другом примере:

Решить систему линейных уравнений:
6*a — b — c = 0
a — 2*b + 3*d = 0
3*a — 4*b — 4*c = -1

• Методом обратной матрицы:
• Методом Гаусса:
• LU разложение:
• QR разложение:

На этом я с вами попрощаюсь, надеюсь, вы научились применять матрицы в Matlab для решения СЛАУ.

Решение и моделирование линейного алгебраическое система уравнение в Matlab

РЕШЕНИЕ И МОДЕЛИРОВАНИЕ ЛИНЕЙНОГО АЛГЕБРАИЧЕСКОЕ СИСТЕМА УРАВНЕНИЕ В MATLAB

Ш. М. Туймуродов (преподаватель, Каршинский филиал ТУИТ)

(магистрантка, Каршинский филиал ТУИТ)

В моделировании разновидные объекты и процессы повстречаются в алгебраической, трансцендентной, линейной и других систем уравнений. Оценить правильность уравнений и решить их в моделировании играет большую роль. Построение уравнений определяются из их особенностей. У всех из таких способов есть свои особенности, чтобы решить их понадобится специальные знания. Увеличение неизвестных построенных моделей и с увеличением виды факторы усложняются их решение. По этому, в решении трудностей использование информационно-коммуникационных технологий облегчает работу и играет нужную роль в получении точного ответа.

Для решении разнотипных математических задач, создана система Matlab, при ней существуют его специальные функции. С помощью этих функций решаются задачи в частном виде.

Мы покажем решение системы линейно-алгебраических уравнений с помощью функций программы Matlab и моделировании в среде Simulink.

Дана система линейно-алгебраического уравнения:

Здесь а11, а22,…….,аnn – неизменяемые коэффициенты, х1, х2,……. хn — неизвестные, b1, b2,……. bn – свободные члены.

Нам требуется решить следующую систему линейно-алгебраического уравнения:

Через окно Command Window системы Matlab, вводим следующие коды, при этом найдется решение системы уравнения.

Для решения системы линейно-алгебраических уравнений (1) из система уравнений определяем следующие матрицы:

A*B=C, отсюда вычисляем неизвестные матрицы B, оно будет выглядеть следующим образом:

,

Здесь A-1 обратная матрица для матрицы A

Чтобы решить систему линейно-алгебраических уравнений в среде матриц, определяем элементы матрицы из системы уравнений и вводим их в окно команд программы Matlab:

>> C=[14;3] % матрица состоит из свободных членов

>> A1=inv(A) %A1 обратная матрица для матрицы

>> B=A1*C % B означает корень уравнения матрицы x1 и x2

Способ моделирования Matlab/Simulink

1-способ: При решении системы уравнений состоящие из неизменяемых чисел вводим каждый эквивалент дифференциальной величины . В среде Matlab/Simulink для произведения модели пишется следующий вид системы уравнений:

Загрузив программную систему Matlab и библиотечную панель Simulink Library Browser, выбераем пользовательский блок: Gain (умножение неизменяемого коэффициента в сигнал ), Constant (источник неизменяемого сигнала ), Integrator (интегральный сигнал), Display (произведение цифрового сигнала в виде числа) Scope (виртуальный оцилограф). В виртуальным осцилографе видно то, что графическая функция означает, что с истечением времени, продолжается часть неизменяемой системы уравнения. А в дисплеи системы уравнение цифрового решения отображается на экране в виде числа. Блок Simulink в составе Matlab для математических задач основан на разработке проектирования, сбора сложных устройств электроники и разработки их математических моделей.

Пользовательские блоки: Display, Constant, Gain, Sum, Integrator, Mux.

Рис 1. Построение моделей системы линейно-алгебраических уравнений и изображения графика в оциллографе

2-способ: Из панели библиотеки отделения Ports&Subsystems выбирается команда Subsystem и настраивается его составная структура, в зависимости от числа неизвестных чисел блоков Gain и увеличивается число блоков multiplexor в зависимости от числа уравнений. Входящие сигналы Multipleksora In1,In2,In3 в выходящие Out1 с раздела Math operations, вращающие на значения ноль вводится Algebraic Constraint. Вводим соответствующие коэффиценты в состав параметров в каждый блок Gain. После процесса моделирования нажимаем кнопку Run и в результате на экране можно увидеть ответ системы уравнений.

Рис 2. Настройка составного строения Мултиплексора

Пользовательские блоки: Subsystem, Display, Constant, Gain, Algebraic Constraint, Sum, Mux.

Рис 3. Схематический состав решения системы линейно — алгебраического уравнения с помощью модели мултиплексора

Таким образом, мы познакомились с системой Matlab и решения систем линейно-алгебраических уравнений помощью стандартных функций матрицы и способами моделирование Simulink. С помощью этих способов создаётся оптимизирование системы произведения, моделирование объектов и процесс оценивания правильности построения моделей и способы их решения. Нужно отметить, что курс «Высшая математика» из точных наук работает с матрицами, выполняет разные операции над ними и разрабатывает разные способы решения линейных уравнений. Особенно с помощью способа Matlab/Simulink моделирование линейных уравнений занимает важное место современной цифровой технике, в изучение телекоммуникационных технологий.

, , . Математическое и компьютерное моделирование процессов и систем в среде MATLAB/SIMULINK. Киев-2008, ст-18-22. Hally More. MATLAB for engineers. Prentice Hall 2012 y. Page.441 MATLAB. Учебное пособие. ГУИА. 2005. – 143 с. , . Методы решения математических задач в Maple. Белгород 2001 г. Ст-22. . Simulink 5/6/7. Самоучитель. ДМК издательство. Москва-2008 г.

Simulink решение системы линейных уравнений

Дифференциальные уравнения и системы уравнений

Необходимо решить уравнение:

Попробуем решить его с помощью программы Simulink пакета MATLAB.

Метод решения дифференциальных уравнений отличается от традиционного. Нам необходимо создать схему уравнения. Необходимо будет создать обратную связь между выходными значениями интегратора и новым значением переменной. У нашего уравнения линейно изменяется x от 0 до 20. Поэтому для решения уравнения необходимо использовать блок Ramp . В конце обязательно должен быть интегрирующий блок, а из него результат выходит на осциллограф.

Решение уравнения выглядит так:

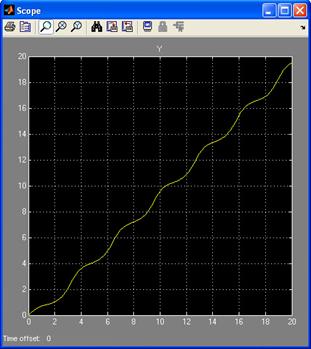
Результатом будет график x от y :

Рассмотрим из каких библиотек взяты использованные блоки.

Ramp – из Sources. Формирует линейный сигнал . В параметрах необходимо задать 1.

Add – Math Operations. В параметрах выбираем необходимые нам операции.

Gain – Math Operations . Коэффициент усиления сигнала. В параметрах ставим значение 3/2.

Sine Wave Function – Sources. Т.к. нам необходим косинус, то в параметрах Phase ставим pi/2.

Integrator – Continuous . Выполняет интегрирование входного сигнала.

Scope – Sinks . Выводим результат – график сигнала в функции времени.

Дифференциальные уравнения 2-го порядка.

Дана система уравнений:

Решим ее с помощью программы Simulink пакета MATLAB.

Решаем аналогично предыдущему случаю.

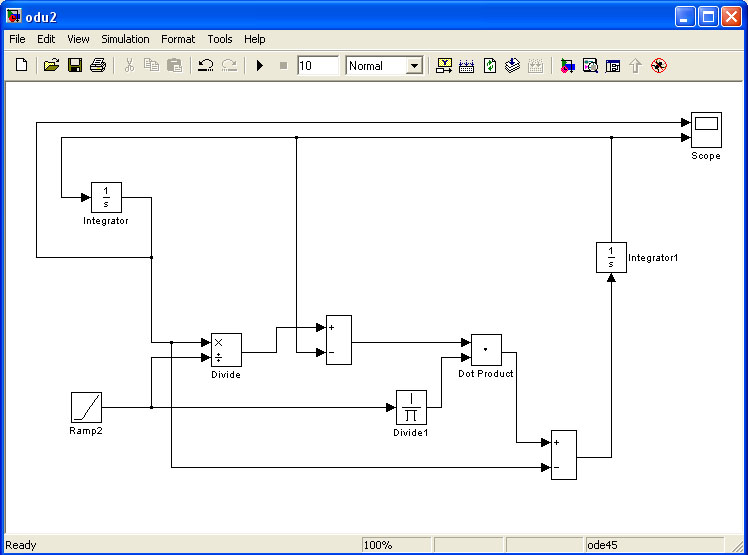
В данной системе уравнений линейно изменяется x от 1 до 10. Также необходимо сделать обратную связь между выходными значениями интеграторов и новым значение переменной x . Обязательно надо в интеграторах задать начальные значения y₁(0) = 0.1; y₂(0) = 0.5.

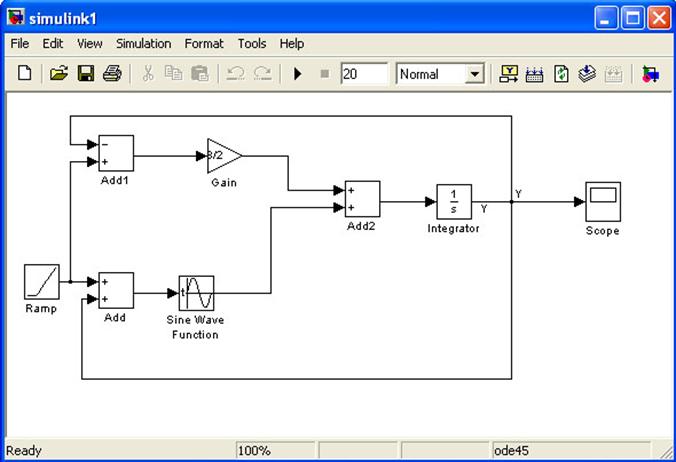
Результатом будут два графика:

Рассмотрим из каких библиотек взяты использованные блоки.

Ramp – из Sources . Формирует линейный сигнал. В параметрах необходимо задать все значения 1.

Integrator – Continuous . Выполняет интегрирование входного сигнала. Необходимо задать начальные значения Initial condition для y ₁ 0.1, для y ₂ 0.5.

Add – Math Operations . В параметрах выбираем необходимые нам операции.

Divide — Math Operations . Деление первой входной величины на вторую.

Dot Product — Math Operations. Перемножение .

Scope – Sinks. Выводим результат – график сигнала в функции времени.