Синус плюс косинус равно 1 решить уравнение

Решение уравнения sin x — cos x = 1. Урок-семинар

Разделы: Математика

Цели урока:

Главная дидактическая цель: рассмотреть все возможные способы решения данного уравнения.

Обучающие: изучение новых приемов решения тригонометрических уравнений на примере данного в творческой ситуации урока-семинара.

Развивающие: формирование общих приемов решения тригонометрических уравнений; совершенствование мыслительных операций учащихся; развитие умений и навыков устной монологической математической речи при изложении решения тригонометрического уравнения.

Воспитывающие: развивать самостоятельность и творчество; способствовать выработке у школьников желания и потребности обобщения изучаемых фактов.

Вопросы для подготовки и дальнейшего обсуждения на семинаре.

Приведение уравнения к однородному относительно синуса и косинуса.
Разложение левой части уравнения на множители.
Введение вспомогательного угла.
Преобразование разности (или суммы) тригонометрических функций в произведение.
Приведение к квадратному уравнению относительно одной из функций.
Возведение обеих частей уравнения в квадрат.
Выражение всех функций через tg x (универсальная подстановка).
Графическое решения уравнения.

Все учащиеся разбиваются на группы (по 2-4 человека) в зависимости от общего количества учащихся и их индивидуальных способностей и желания. Самостоятельно определяют для себя тему для подготовки и выступления на уроке-семинаре. Выступает один человек от группы, а остальные учащиеся принимают участие в дополнениях и исправлениях ошибок, если в этом возникнет необходимость.

Организационный момент.

Тема урока:

“Различные способы решения тригонометрического уравнения sin x — cos x = 1

Форма проведения: урок – семинар.

Эпиграф к уроку:

“Крупное научное открытие дает решение крупной проблемы, но и в решении любой задачи присутствует крупица открытия. Задача, которую вы решаете, может быть скромной, но если она бросает вызов вашей любознательности и заставляет вас быть изобретательными и если вы решаете ее собственными силами, то вы сможете испытать ведущее к открытию напряжение ума и насладиться радостью победы”

Задачи урока:

а) рассмотреть возможность решения одного и того же уравнения различными способами;
б) познакомиться с различными общими приемами решения тригонометрических уравнений;
в) изучение нового материала (введение вспомогательного угла, универсальная подстановка).

План семинара

Приведение уравнения к однородному относительно синуса и косинуса.
Разложение левой части уравнения на множители.
Введение вспомогательного угла.
Преобразование разности (или суммы) тригонометрических функций в произведение.
Приведение к квадратному уравнению относительно одной из функций.
Возведение обеих частей уравнения в квадрат.
Выражение всех функций через tg x (универсальная подстановка).
Графическое решения уравнения.

Содержание.

1. Слово предоставляется первому участнику.

Приведение уравнения sin x — cos x = 1 к однородному относительно синуса и косинуса.
Разложим левую часть по формулам двойного аргумента, а правую часть заменим тригонометрической единицей, используя основное тригонометрическое тождество:

2 sin cos — cos + sin = sin + cos ;

2 sin cos — cos =0 ;
cos = 0;
Произведение равно нулю, если хотя бы один из множителей равен нулю, а другие при этом не теряют смысла, поэтому следует

cos =0 ; =

= 0 — однородное уравнение первой степени. Делим обе части уравнения на cos . (cos 0, так как если cos = 0 , то sin — 0 = 0 sin = 0, а это противоречит тригонометрическому тождеству sin + cos = 1).

Получим tg -1 = 0 ; tg = 1 ; =
Ответ:
2. Слово предоставляется второму участнику.

Разложение левой части уравнения sin x — cos x = 1 на множители.

sin x – (1+ cos x ) = 1; используем формулы 1+ cos x = 2 , получим ;
далее аналогично:

произведение равно нулю, если хотя бы один из множителей равен нулю, а другие при этом не теряют смысла, поэтому следует

cos =0 ; =
= 0 — однородное уравнение первой степени. Делим обе части уравнения на cos . (cos 0, так как если cos = 0 , то sin — 0 = 0 sin = 0, а это противоречит тригонометрическому тождеству sin + cos = 1)

Получим tg -1 = 0 ; tg = 1 ; =
Ответ:

3. Слово предоставляется третьему участнику.

Решение уравнения sin x — cos x = 1 введением вспомогательного угла.

Рассмотрим уравнение sin x — cos x = 1. Умножим и разделим каждое слагаемое левой части
уравнения на . Получим и вынесем в левой части уравнения за скобку. Получим ; Разделим обе части уравнения на и используем табличные значения тригонометрических функций. Получим ; Применим формулу синус разности.
;

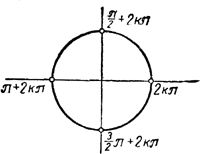
Легко установить(с помощью тригонометрического круга), что полученное решение распадается на два случая:

;

Ответ:

4. Слово предоставляется четвертому участнику.

Решение уравнения sin x — cos x = 1 способом преобразования разности (или суммы) тригонометрических функций в произведение.

Запишем уравнение в виде , используя формулу приведения . Применяя формулу разности двух синусов, получим

;

и так далее, аналогично предыдущему способу.

Ответ:

5. Слово предоставляется пятому участнику.

Решение уравнения sin x — cos x = 1 способом приведения к квадратному уравнению относительно одной из функций.

Рассмотрим основное тригонометрическое тождество , откуда следует
подставим полученное выражение в данное уравнение.
sin x — cos x = 1 ,

Возведем обе части полученного уравнения в квадрат:

В процессе решения обе части уравнения возводились в квадрат, что могло привести к появлению посторонних решений, поэтому необходима проверка. Выполним ее.

Полученные решения эквивалентны объединению трех решений:

Первое и второе решения совпадают с ранее полученными, поэтому не являются посторонними. Остается проверить третье решение Подставим.
Левая часть:

Получили: , следовательно, – постороннее решение.

Ответ:

6. Слово предоставляется шестому участнику.

Возведение обеих частей уравнения sin x — cos x = 1 в квадрат.

Рассмотрим уравнение sin x — cos x = 1. Возведем обе части данного уравнения в квадрат.

;

Используя основное тригонометрическое тождество и формулу синуса двойного угла, получим ; sin 2x = 0 ; .

Полученное решение эквивалентно объединению четырех решений:

(эти решения можно нанести на единичную окружность). Проверка показывает, что первое и четвертое решения — посторонние.

Ответ:

7. Слово предоставляется седьмому участнику.

Использование универсальной подстановки в решении уравнения sin x — cos x = 1. Выражение всех функций через tg x по формулам:

Запишем данное уравнение с учетом приведенных формул в виде .
,

получим

ОДЗ данного уравнения – все множество R. При переходе к из рассмотрения выпали значения, при которых не имеет смысла, т. е. или .

Следует проверить, не являются ли решениями данного уравнения. Подставим в левую и правую часть уравнения эти решения.

Левая часть: .

Получили 1=1. Значит, — решение данного уравнения.

Ответ:

8. Слово предоставляется восьмому участнику.

Рассмотрим графическое решение уравнения sin x — cos x = 1.

Запишем рассматриваемое уравнение в виде sin x = 1 + cos x.

Построим в системе координат Оxy графики функций, соответствующих левой и правой частям уравнения. Абсциссы точек пересечения графиков являются решениями данного уравнения.

y = sin x – график: синусоида.
y = cos x +1 – график: косинусоида y = cos x, смещенная на 1 вверх по оси Oy. Абсциссы точек пересечения являются решениями данного уравнения.

Ответ:

Итог урока.

Учащиеся научились решать тригонометрические уравнения вида , освоили новый материал.
На примере одного уравнения рассмотрели несколько способов решения.
Учащиеся были непосредственными участниками урока, была задействована обратная связь в системе ученик-учитель.
Учащиеся получили навыки самостоятельной работы с дополнительной литратурой.

Список использованной литературы:

Татарченкова С.С. Урок как педагогический феномен – Санкт-Петербург: Каро, 2005
Выгодский Н.В. Справочник по элементарной математике.-М.: Наука, 1975.
Виленкин Н.Я. и др. За страницами учебника математики: Арифметика. Алгебра. Геометрия: Книга для учащихся 10-11 класса – М.: Просвещение, 1996.
Гнеденко Б.В. Очерки по истории математики в России – М.: ОГИЗ, 1946.
Депман И.Я. и др. За страницами учебника математики – М.: Просвещение, 1999.
Дорофеев Г.В. и др. Математика: для поступающих в вузы – М.: Дрофа, 2000.
Математика: Большой энциклопедический словарь. – М.: БСЭ, 1998.
Мордкович А.Г. и др. Справочник школьника по математике. 10-11кл. Алгебра и начала анализа. – М.: Аквариум, 1997.
300 конкурсных задач по математике. – М.: Рольф, 2000.
3600 задач по алгебре и началам анализа. – М.: Дрофа, 1999.
Школьная программа в таблицах и формулах. Большой универсальный справочник. – М.: Дрофа, 1999.
Торосян В.Г. История образования и педагогической мысли: учеб. для студентов вузов. — М.: Изд-во ВЛАДОС-ПРЕСС, 2006.- 351 с.
Крылова Н.Б. Педагогическая, психологическая и нравственная поддержка как пространство личностных изменений ребёнка и взрослого.// Классный руководитель.- 2000.- №3. –С.92-103.

Синус плюс косинус равно 1 решить уравнение

Возведя обе части данного уравнения в квадрат, мы получим:

sin 2 х + 2 sin x cos x + cos 2 x = 1,

Поскольку обе части данного уравнения мы возводили в квадрат,то не исключена возможность, что среди полученных нами корней имеются посторонние. Вот почему в этом примере, в отличие от всех предыдущих, необходимо сделать проверку. Все значения х = π /₂ n можно разбить на 4 группы

При х = 2kπ sin x + cos x = 0 + 1 = 1. Следовательно, х = 2kπ — корни данного уравнения.

При х = π + 2kπ sin x + cos x = 0 — 1 = — 1. Поэтому значения х = π + 2kπ не являются корнями данного уравнения. Аналогично показывается, что х = 3π /₂ + 2kπ. не являются корнями.

Таким образом, данное уравнение имеет следующие корни: х = 2kπ и х = π /₂ + 2mπ., где k и m — любые целые числа.

Урок — семинар на тему «Решение уравнения sin x + cos x = 1»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Муниципальное бюджетное образовательное учреждение

средняя образовательная школа №1

имени генерал – лейтенанта Б.П. Юркова

г.Зверева Ростовской области.

Урок — семинар на тему

учитель математики МБОУ СОШ №1

Куц Фёдор Иванович

Перед человеком к разуму три пути: путь размышления — это самый благородный; путь подражания — это самый легкий; путь личного опыта — самый тяжелый путь.

Главная дидактическая цель: рассмотреть все возможные способы решения данного уравнения.

Вопросы для подготовки и дальнейшего обсуждения на семинаре.

1) Введение вспомогательного угла.

2) Использование универсальной тригонометрической подстановки:

3) Сведение к однородному уравнению.

4) Применением формул сложения тригонометрических функций

5) Возведение обеих частей уравнения в квадрат.

6) Применение формул двойного и половинного аргумента.

7) Применение основного тригонометрического тождества.

8) Приведение к квадратному уравнению относительно одной из функций.

9)Графическое решение уравнения.

Все учащиеся разбиваются на группы (по 2-3 человека) в зависимости их индивидуальных способностей и желания. Каждой группе определяется задание для подготовки и выступления на уроке-семинаре. Выступает один человек от группы, а остальные учащиеся принимают участие в дополнениях и исправлениях ошибок, если в этом возникнет необходимость.

Тема урока: «Различные способы решения тригонометрического уравнения sin x + cos x = 1».

Форма проведения: урок – семинар.

а) рассмотреть возможность решения одного и того же уравнения различными способами;

б) познакомиться с различными общими приемами решения тригонометрических уравнений;

в) изучение нового материала (введение вспомогательного угла, универсальная подстановка).

1) Введение вспомогательного угла.

2) Использование универсальной тригонометрической подстановки:

3) Сведение к однородному уравнению.

4) Применением формул сложения тригонометрических функций

5) Возведение обеих частей уравнения в квадрат.

6) Применение формул двойного и половинного аргумента.

7) Применение основного тригонометрического тождества.

8) Приведение к квадратному уравнению относительно одной из функций.

9)Графическое решение уравнения.

Решение первой группы.

Решение уравнения sin x + cos x = 1 методом « Введения вспомогательного угла».

Если дано уравнение a sin x + b cos x = с , то разделив обе части уравнения на выражение

и вводя дополнительный угол , получим уравнение cos sin x + sin cos x = .

Откуда sin ( x + ) = .

( Или sin sin x + cos cos x = . Откуда cos ( x + ) = ).

Для уравнения sin x + cos x = 1 имеем: a = 1, b = 1: = = .

sin x + cos x = ; sin x + cos x = .

cos sinx + sin cosx = , sin(x + ) = ; x + = (- 1) n arcsin + π n, n Z;

x + = (- 1) n + π n, n Z; x = — + (- 1) n + π n, n Z.

Эта серия корней распадается на две серии :

при четном n : n = 2m x = — + + 2 πm = 2π m , m Z ;

при нечетном n : n = 2 k + 1 x = — — + π (2 k + 1) = — + π + 2π k = = + 2π k , k Z .

Ответ. x = 2π n , n Z ; x = + 2π k , k Z .

Или 2) sin sinx + cos cosx = ; cos(x — ) = ; x — = ± arccos + 2π n, n Z;

x — = ± + 2π n, n Z; x = ± + 2π n, n Z.

Эта серия корней распадается на две серии : x = 2π n , n Z ; x = + 2π k , k Z .

Ответ. x = 2π n , n Z ; x = + 2π k , k Z .

Решение второй группы.

Решение уравнения sin x + cos x = 1 с помощью универсальной тригонометрической подстановки: sin x = , cos x = .

Перепишем данное уравнение с учетом приведенных формул:

+ = 1. Умножим обе части уравнения на общий знаменатель ( ≠0).

+ = ; — = 0; ( — 1) = 0.

= 0 или — 1 = 0.

1) = 0, = π n , n Z ; x = 2π n , n Z .

2) = 1, = + π k, k Z; x = + 2 π k, k Z.

Ответ . x = 2 π n, n Z; x = + 2 π k, k Z.

3. Решение третьей группы.

Решение уравнения sin x + cos x = 1 приведением к однородному уравнению относительно синуса и косинуса.

Используя формулы двойного аргумента sin x = 2 sin cos , cosx = cos 2 — sin 2 и записывая

правую часть уравнения в виде 1= cos 2 + sin 2 , получаем:

2sin cos + cos 2 — sin 2 = cos 2 + sin 2 ; 2 sin 2 — 2sin cos = 0.

Вынося 2 sin за скобки, получим равносильное уравнение

2 sin (sin – cos = 0. Произведение равно нулю, если хотя бы один из множителей равен

нулю, другие при этом имеют смысл. Следовательно, 2 sin = 0 или sin – cos

1) sin = 0. = n, n Z; x = 2 π n, n Z.

2) sin — cos = 0 – однородное уравнение первой степени. Делим обе части уравнения на cos

( cos ≠ 0, в противном случае, если cos = 0, то и sin = 0, что противоречит основному

тригонометрическому тождеству cos 2 + sin 2 = 1).

tg — 1= 0; tg = 1.

= + х = + 2 π k , k Z .

Ответ. x = 2π n , n Z ; x = + 2π k , k Z .

4. Решение четвертой группы.

Решение уравнения sin x + cos x = 1 с применением формул сложения тригонометрических

функций sin + sin = 2 sin cos .

Выразим cos x через sin x , используя формулы приведения: cos x = sin ( — x ).

sin x + sin ( — x) = 1; 2 sin cos = 1; 2 sin cos (x — ) = 1;

2∙ ∙ cos (x — ) = 1; cos (x — ) = .

x — = ± arccos + 2 n, n Z; x = ± + 2 n, n Z.

x = 2 n, n Z; х = + 2 k, k Z .

Ответ . x = 2 π n, n Z; x = + 2 π k, k Z.

5. Решение пятой группы.

Решение уравнения sin x + cos x = 1 способом возведения обеих частей уравнения в квадрат.

(sin x + cos x ) 2 = 1; sin 2 x + 2sin x cos x + cos x 2 = 1.

Используя формулу синуса двойного аргумента sin 2 x = 2 sin x cos x и основное

тригонометрическое тождество cos 2 х + sin 2 х = 1, имеем:

sin 2x + 1 = 1; sin 2x = 0; 2x = π n, n Z; x = , n Z.

При возведении уравнения в квадрат получаем уравнение – следствие, поэтому проведем

1) При х = 2π n , n Z , 0 + 1 = 1 верно, х = 2π n , n Z – корни уравнения.

2) При х = + 2π n , n Z ; 1+ 0 = 1 верно, х = + 2π n , n Z – корни уравнения.

3) При х = π + 2π n , n Z , 0 — 1 = 1 неверно, х = π + 2π n , n Z – не являются корнями

4) При х = + 2π n , n Z , -1+ 0 = 1 неверно, х = + 2π n , n Z – не являются корнями

Ответ. x = 2π n , x = + 2π n , n Z .

6. Решение шестой группы.

Решение уравнения sin x + cos x = 1 с применение формул двойного и половинного

Запишем уравнение в виде: sin x = 1 — cos x .

Сделаем замену : sin x = 2sin cos , 1 — cos x = 2 sin 2 .

2sin cos = 2sin 2 ; 2sin cos — 2sin 2 = 0. Вынося 2 sin за скобки, получим равносильное

уравнение 2 sin ( sin – cos = 0. Произведение равно нулю, если хотя бы один из множителей

равен нулю, а другие при этом не теряют смысла.

2sin = 0 или cos — sin = 0.

1) 2sin = 0; = π n, n Z; x = 2 π n, n Z.

2) cos = sin ; = 1; = + π k; x = + 2 π k, k Z.

Ответ . x = 2 π n, n Z; x = + 2 π k, k Z.

7. Решение седьмой группы.

Решение уравнения sin x + cos x = 1 с применение основного тригонометрического

Из тождества sin 2 x + cos 2 x = 1 имеем cos 2 x = 1 — sin 2 x , откуда cos x = ± .

sin x ± = 1; ± = 1 – sin x; 1 — sin 2 x = (1 – sin x) 2 ;

(1- sin x) (1 + sin x) — (1 – sin x) 2 = 0; (1- sin x) (1 + sin x – 1 + sin x) = 0; (1 — sin x) ∙ 2sin x = 0.

1 – sin x = 0 или 2 sin x = 0.

1) sin x = 1; x = + 2 π k, k Z.

2) sin x = 0; x = π n , n Z .

В процессе решения обе части уравнения возводились в квадрат, что могло

привести к появлению посторонних решений, поэтому необходима проверка.

При х = + 2π k , k Z , 1+ 0 = 1 верно, х = + 2π k , k Z .– корни уравнения.

При х = 2π n , n Z , 0 + 1 = 1 верно, х = 2π n , n Z – корни уравнения.

При х = π + 2π n , n Z , 0 — 1 = 1 неверно, х = π + 2π n , n Z – не являются корнями уравнения.

Ответ. x = 2π n , n Z ; x = + 2π k , k Z .

8. Решение восьмой группы.

Решение уравнения sin x + cos x = 1 способом приведения к квадратному уравнению

относительно одной из функций.

Рассмотрим основное тригонометрическое тождество sin 2 x + cos 2 x = 1 , откуда следует sin x =

± , подставим полученное выражение в данное уравнение.

± + cos x = 1; ± = 1 — cos x .

Возведем обе части полученного уравнения в квадрат: 1 – cos 2 x = 1 – 2 cos x + cos 2 x ;

2cos 2 x — 2cos x = 0; cos x (cos x – 1) = 0.

cos x = 0 или cos x – 1 = 0.

1) cos x = 0. x = + π k, k Z.

2) cos x – 1 = 0; cos x =1. х = 2 π n, n Z.

Корни необходимо проверить.

При х = + 2π k , k Z , 1+ 0 = 1 верно, х = + 2π k , k Z – корни уравнения.

При х = — + 2π k , k Z , — 1 + 0 = 1 неверно, х = — + 2π k , k Z – не являются корнями

При х = 2π n , n Z , 0 + 1 = 1 верно, х = 2π n , n Z – корни уравнения.

Ответ. x = 2π n , n Z ; x = + 2π k , k Z .

9. Решение девятой группы.

Решение уравнения sin x + cos x = 1 графическим способом

Перепишем уравнение в виде: sin x = 1 — cos x.

Построим в одной системе координат графики функций : у = sin x , y =1 — cos x.

Абсциссы точек пересечения являются решениями данного уравнения.

Из графика видно, что уравнение имеет 2 решения: x = 2π n , n Z ; x = + 2π k , k Z . (Необходимо обязательно проверять это вычислениями).

Ответ. x = 2π n , n Z ; x = + 2π k , k Z .

Учащиеся научились решать тригонометрические уравнения вида a sin x + b cos x = c , освоили новый материал.

На примере одного уравнения рассмотрели несколько способов решения.

Учащиеся были непосредственными участниками урока, была задействована обратная связь в системе ученик-учитель.

Учащиеся получили навыки самостоятельной работы с дополнительной литературой.

1. Материалы курса «Тригонометрия в школе». /Н.Н. Решетников, М. Педагогический университет «Первое сентября», 2010 г.

2. Математика. Большой справочник школьников и поступающих в вузы. М.»дрофа»,1999 г.

3. Математика. Учебное пособие для слушателей подготовительных курсов. Новочеркасск, НГМА,2003 г.

4.Алгебра и начала анализа. 10 -11 классы: учебник для общеобразовательных учреждений: базовый уровень/ Ш.А. Алимов и др./ — М, Просвещение, 2010 г.

источники:

http://razdupli.ru/primer-602

http://infourok.ru/urok-seminar-na-temu-reshenie-uravneniya-sin-cos-286873.html