Система дифференциальных уравнений частных производных matlab

Применение MATLAB для решения уравнений в частных производных

Для своего варианта функционала выведите дифференциальное уравнение Эйлера-Остроградского и решите его c помощью PDE Toolbox MATLAB.

Примечание: Если на рисунке указано “r = ” – то это часть окружности, если символа “r ” нет – то часть эллипса.

Начало координат − в левом нижнем углу. Граничные условия: на верхней дуге u = 10−3(y−0.15), на остальных сторонах u = 0.

Приложить файл для программы PDE Toolbox MATLAB.
Ниже указан пример готового решения задачи

Применение MATLAB для решения уравнений в частных производных

Рассмотрим графические возможности МАТЛАБ на примере вывода решения дифференциального уравнения в частных производных Эйлера-Остроградского.

Пример 1. Найти экстремаль функционала:

в прямоугольной области xÎ[0,a]; yÎ [0,b], показанной на рис.3.

Рис.3. Область решения примера 1

Граничные условия: на правой стороне x = a:

на остальных сторонах z = 0.

Выведем вначале уравнение Эйлера-Остроградского вида:

,

или, после сокращения на 2:

. (8)

Граничные условия по переменной y однородные, поэтому будем искать решение в виде ряда Фурье по собственным функциям Yn(y), которые равны:

.

Ищем решение в виде ряда:

. (9)

Это решение удовлетворяет граничным условиям на нижней и верхней сторонах: при y=0 и y=b.

Для нахождения функций Xn(x) подставим решение (9) в уравнение (8):

.

Левая часть данного уравнения является разложением в ряд Фурье по Yn(y). Разложим в такой же ряд правую часть этого уравнения. Собственно, она уже разложена: в этом ряду присутствует только первый член (n=1), а коэффициенты при остальных гармониках равны нулю. Известно, что два ряда Фурье тождественны друг другу тогда и только тогда, когда равны все их коэффициенты. Поэтому из полученного уравнения можно получить бесконечную систему дифференциальных уравнений для функций Xn(x):

(10)

Граничные условия для данного уравнения можно получить, раскладывая граничные условия на левой и правой сторонах в ряд Фурье по Yn(y). На левой стороне x=0 имеем z=0, и, следовательно, коэффициенты разложения данной функции нулевые:

. (11)

На правой стороне x=a имеем граничное условие:

Подставим в него решение (9):

Это возможно тогда и только тогда, когда:

(12)

Решаем систему дифференциальных уравнений (10) при граничных условиях (11) и (12). При n>1 имеем:

;

. (13)

Подставляем граничные условия:

Во втором уравнении второй множитель (гиперболический синус) не равен нулю, поэтому C2=0. Следовательно, .

Далее найдем X1(x). Дифференциальное уравнение для него – это 1-е уравнение системы (10). Для решения такого уравнения следует взять сумму общего решения соответствующего однородного уравнения вида (13) и частного решения неоднородного уравнения. В результате получим:

Значения произвольных постоянных С1 и С2 найдем из граничных условий (11) и (12):

.

Решением рассматриваемой задачи является первая гармоника ряда:

График (рис.4) этой функции при a = 1 и b = 2 выглядит следующим образом:

clear all % очистили память

a=1; % задали размеры

[X, Y]=meshgrid(x, y); % сетка

b^2*X/pi^2).*sin(pi*Y/b); % вычисляем функцию

surf(X, Y,U) % рисуем поверхность

‘FontName’,’Times New Roman Cyr’,’FontSize’,12)

da=daspect; % текущие масштабы осей

da(1:2)=min(da(1:2)); % одинаковые масштабы

daspect(da); % установили одинаковые масштабы

title(‘\bf Пример 1’)

xlabel(‘\itx’) % ось OX

ylabel(‘\ity’) % ось OY

zlabel(‘\itu\rm(\itx\rm,\ity\rm)’) % ось OZ

MATLAB — Дифференциал

MATLAB предоставляет команду diff для вычисления символьных производных. В простейшей форме вы передаете функцию, которую вы хотите дифференцировать, команде diff в качестве аргумента.

Например, давайте вычислим производную функции f (t) = 3t 2 + 2t -2

пример

Создайте файл сценария и введите в него следующий код —

Когда приведенный выше код компилируется и выполняется, он дает следующий результат —

Ниже приведен октавный эквивалент приведенного выше расчета —

Octave выполняет код и возвращает следующий результат —

Проверка элементарных правил дифференциации

Кратко сформулируем различные уравнения или правила дифференцирования функций и проверим эти правила. Для этого мы напишем f ‘(x) для производной первого порядка и f «(x) для производной второго порядка.

Ниже приведены правила для дифференциации —

Правило 1

Для любых функций f и g и любых действительных чисел a и b являются производными функции —

h (x) = af (x) + bg (x) относительно x определяется как —

Правило 2

Правила сумм и вычитаний гласят, что если f и g две функции, то f ‘и g’ являются их производными соответственно, тогда

Правило 3

Правило произведения гласит, что если f и g две функции, f ‘и g’ являются их производными соответственно, то

Правило 4

Правило отношения гласит, что если f и g две функции, f ‘и g’ являются их производными соответственно, то

Правило 5

Полиномиальное или элементарное степенное правило гласит, что если y = f (x) = x n , то f ‘= n. х (н-1)

Прямым результатом этого правила является то, что производная любой константы равна нулю, т. Е. Если y = k , любая константа, то

Правило 6

Правило цепочки гласит, что производная функции функции h (x) = f (g (x)) по x равна

пример

Создайте файл сценария и введите в него следующий код —

Когда вы запускаете файл, MATLAB отображает следующий результат —

Ниже приведен октавный эквивалент приведенного выше расчета —

Octave выполняет код и возвращает следующий результат —

Производные экспоненциальных, логарифмических и тригонометрических функций

В следующей таблице приведены производные от часто используемых экспоненциальных, логарифмических и тригонометрических функций.

пример

Создайте файл сценария и введите в него следующий код —

Когда вы запускаете файл, MATLAB отображает следующий результат —

Ниже приведен октавный эквивалент приведенного выше расчета —

Octave выполняет код и возвращает следующий результат —

Вычисление производных высшего порядка

Для вычисления старших производных функции f мы используем синтаксис diff (f, n) .

Вычислим вторую производную функции y = f (x) = x .e -3x

MATLAB выполняет код и возвращает следующий результат —

Ниже приведен октавный эквивалент приведенного выше расчета —

Octave выполняет код и возвращает следующий результат —

пример

В этом примере давайте решим проблему. Учитывая, что функция y = f (x) = 3 sin (x) + 7 cos (5x) . Нам нужно выяснить, выполняется ли уравнение f «+ f = -5cos (2x) .

Создайте файл сценария и введите в него следующий код —

Когда вы запускаете файл, он показывает следующий результат —

Ниже приведен октавный эквивалент приведенного выше расчета —

Octave выполняет код и возвращает следующий результат —

Нахождение максимумов и минимумов кривой

Если мы ищем локальные максимумы и минимумы для графика, мы в основном ищем самые высокие или самые низкие точки на графике функции в определенной местности или для определенного диапазона значений символической переменной.

Для функции y = f (x) точки на графе, где граф имеет нулевой наклон, называются стационарными точками . Другими словами, стационарные точки — это где f ‘(x) = 0.

Чтобы найти стационарные точки функции, которую мы дифференцируем, нам нужно установить производную равной нулю и решить уравнение.

пример

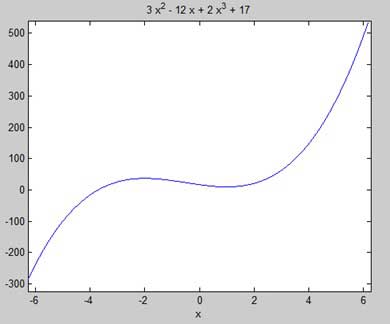
Найдем стационарные точки функции f (x) = 2x 3 + 3x 2 — 12x + 17

Сделайте следующие шаги —

Сначала давайте введем функцию и построим ее график.

MATLAB выполняет код и возвращает следующий график —

Вот октавный эквивалентный код для приведенного выше примера —

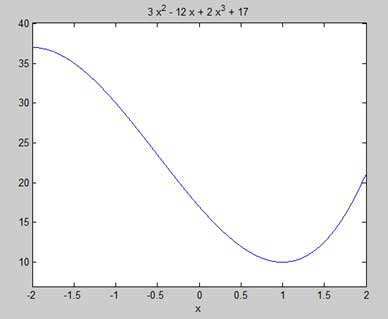
Наша цель — найти некоторые локальные максимумы и минимумы на графике, поэтому давайте найдем локальные максимумы и минимумы для интервала [-2, 2] на графике.

MATLAB выполняет код и возвращает следующий график —

Вот октавный эквивалентный код для приведенного выше примера —

Далее, давайте вычислим производную.

MATLAB выполняет код и возвращает следующий результат —

Вот октавный эквивалент приведенного выше расчета —

Octave выполняет код и возвращает следующий результат —

Давайте решим производную функцию g, чтобы получить значения, где она становится равной нулю.

MATLAB выполняет код и возвращает следующий результат —

Ниже приведен октавный эквивалент приведенного выше расчета —

Octave выполняет код и возвращает следующий результат —

Это согласуется с нашим сюжетом. Итак, давайте оценим функцию f в критических точках x = 1, -2. Мы можем подставить значение в символическую функцию с помощью команды subs .

MATLAB выполняет код и возвращает следующий результат —

Ниже приведен октавный эквивалент приведенного выше расчета —

Следовательно, минимальное и максимальное значения для функции f (x) = 2x 3 + 3x 2 — 12x + 17 в интервале [-2,2] составляют 10 и 37.

Решение дифференциальных уравнений

MATLAB предоставляет команду dsolve для символического решения дифференциальных уравнений.

Наиболее простой формой команды dsolve для поиска решения одного уравнения является

где eqn — текстовая строка, используемая для ввода уравнения.

Он возвращает символическое решение с набором произвольных констант, которые MATLAB помечает C1, C2 и так далее.

Вы также можете указать начальные и граничные условия для задачи в виде списка с разделителями-запятыми после уравнения в виде —

В целях использования команды dsolve производные обозначены знаком D. Например, уравнение типа f ‘(t) = -2 * f + стоимость (t) вводится как —

‘Df = -2 * f + cos (t)’

Высшие производные обозначены следующим за D порядком производной.

Например, уравнение f «(x) + 2f ‘(x) = 5sin3x должно быть введено как —

‘D2y + 2Dy = 5 * sin (3 * x)’

Давайте рассмотрим простой пример дифференциального уравнения первого порядка: y ‘= 5y.

MATLAB выполняет код и возвращает следующий результат —

Давайте рассмотрим другой пример дифференциального уравнения второго порядка: y «- y = 0, y (0) = -1, y ‘(0) = 2.

MATLAB выполняет код и возвращает следующий результат —

Решение систем дифференциальных уравнений в MATLAB

Решение систем дифференциальных уравнений.

Для решения систем дифференциальных уравнений существует несколько встроенных процедур. Рассмотрим применение процедуры ode45. Как один из возможных форматов вызова, можно предложить такой: [t,r]=ode45(@DiffEquationFunction,[Tstart,Tfinish], StartVector). Отметим, что процедура ode45 может решить систему уравнений следующего вида: , где — есть векторная функция .

Рассмотрим пример, иллюстрирующий создание исходной функции DiffEquationFunction для вызова ее процедурой ode45. Пусть некоторая точка массы движется в гравитационном поле неподвижных точек с массами и (см. рис.). Уравнение сил в гравитационном поле точек и будет следующим: . Как видим, данное дифференциальное уравнение имеет второй порядок. Но его можно свести к системе дифференциальных уравнений первого порядка: .

Будем считать, что данная задача является «плоской» и введем следующие обозначения: , , и . Исходя из таких обозначений, систему дифференциальных уравнений движения точки в гравитационном поле можно представить следующим образом: .

Без ущерба для сути решения, значение гравитационной постоянной примем равной 1, , , , .

В таком виде систему уравнений можно уже записать как файл-функцию, что мы и сделали, назвав ее threepoint(t,x).

M1=50; M2=0; C1x=5; C1y=0; C2x=0; C2y=10;

Решим систему дифференциальных уравнений, вызвав процедуру ode45 из файла-функции dynpoint.m.

x1=5; y1=0; x2=0; y2=10;

При таких начальных параметрах ( ) наша точка движется в поле одного объекта.

То, что мы получили вполне можно назвать приемлемым результатом. Нашей целью являлась корректная подготовка системы дифференциальных уравнений для ее решения процедурой ode45. С другой стороны, применяя иные встроенные процедуры можно получить отличающиеся в корне результаты.

Попробуем немного поэкспериментировать и введем значение . Это должно внести возмущения в орбиту движущейся точки.

Крестиком и звездочкой на графике отмечены соответственно и . Помимо процедуры ode45 существует еще ряд встроенных процедур решения систем дифференциальных уравнений. Их описание можно найти в книгах, указанных в списке литературы. Поскольку, решение систем дифференциальных уравнений является очень важным моментом, то мы не ограничимся одним примером.

Рассмотрим следующую задачу, опять же из физики. Рассмотрим траекторию движения пули под действием силы тяжести. При отсутствии сопротивления воздуха, как известно из курса средней школы, это будет парабола. Мы же рассмотрим случай, когда сила сопротивления воздуха пропорциональна квадрату скорости и противоположна направлению движения. Как говорит школьный курс физики, уравнение баланса сил будет следующим: . Учитывая то, что ускорение – производная скорости по времени, распишем это уравнение в векторном виде: . Где — плотность воздуха, — масса пули, — площадь поперечного сечения. Распишем это уравнение покоординатно: . В таком виде система дифференциальных уравнений готова для того, чтобы попытаться решить ее при помощи процедуры ode45. Пусть масса пули – 10 грамм, поперечник – 1 см 2 , плотность воздуха – 1 кг/м 3 . С такими данными мы составим файл-функцию airpoint.m.

g=10; ro=1; s=0.0001; m=0.01; k=ro*s/(2*m);

В такой системе уравнений аргументом являются скорость и время. Если мы хотим найти траекторию движения, то мы должны принять во внимание: . Полученные массивы точек , , можно в дальнейшем обработать. Произвести интерполяцию, аппроксимацию и т.д. Но мы интегрирование заменим суммированием: . В этом случае начальный момент времени равен 0, пуля находится в начале координат. Создадим файл-функцию dynairpoint, в которой вызовем процедуру ode45. В начальный момент времени скорость пули по горизонтали 800, по вертикали – 100.