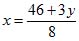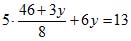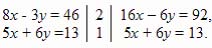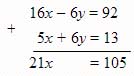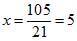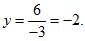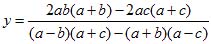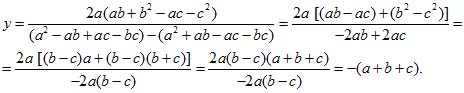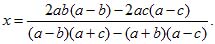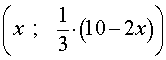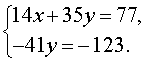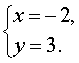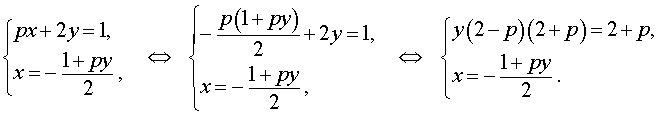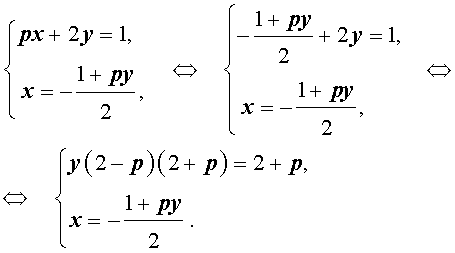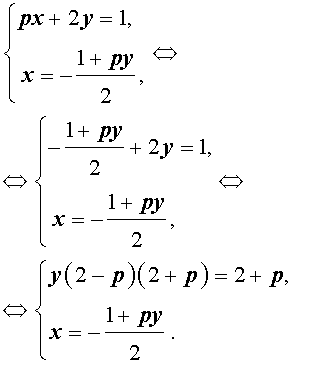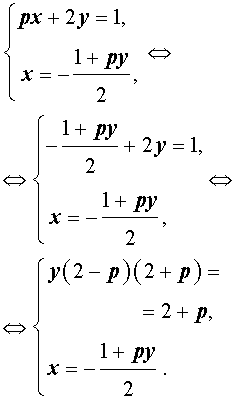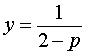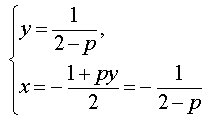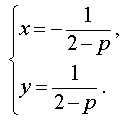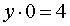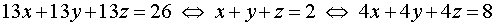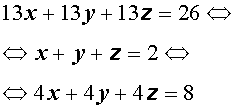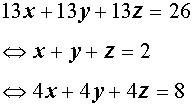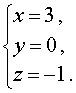Система из двух уравнений первой степени
а) Способ подстановки состоит в том, что:
1) из одного уравнения мы находим выражение одного из неизвестных, например x, через известные величины и другое неизвестное у,
2) найденное выражение подставляем во второе уравнение, в котором после этой подстановки будет содержаться только одно неизвестное у;
3) решаем полученное уравнение и находим значение у; 4) подставляя найденное значение у в выражение неизвестного x, найденное в начале решения, получаем значение х.
Пример. Решить систему уравнений:
8x – 3y = 46, 5x + 6y = 13.
1) Из первого уравнения находим выражение х через данные числа и неизвестное у:
2) Подставляем это выражение во второе уравнение:
3) Решаем полученное уравнение:
5(46+3y)/8 + 48y/8 = 13, 5(46+3y) + 48y = 104, 230 + 15y + 48y = 104, 15y+48y = 104 – 230, 63y = — 126, y = — 2.
4) Найденное значение y = — 2 подставляем в выражение 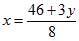
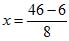
Способ сложения или вычитания
1) обе части одного уравнения умножаются на некоторый множитель; обе части второго уравнения умножаются на другой множитель. Эти множители подбираются так, чтобы коэффициенты при одном из неизвестных в обоих уравнениях после их умножения на эти множители имели одну, и ту же абсолютную величину.
2) Складываем два уравнения или вычитаем их друг из друга, смотря по тому, имеют ли уравненные коэффициенты различные или одинаковые знаки; этим одно из неизвестных исключается.
3) Решаем полученное уравнение с одним неизвестным.
4) Другое неизвестное можно найти тем же приемом, но обычно, проще всего подставить найденное значение первого неизвестного в любое из данных уравнений и решить получившееся уравнение с одним неизвестным.
Пример. Решить систему уравнений:
8x – 3y = 46, 5x + 6y = 13.
1) Проще всего уравнять абсолютные величины коэффициентов при у; обе части первого уравнения умножим на 2; обе части второго — на 1, т. е. оставляем второе уравнение неизменным:
2) Складываем два уравнения:
3) Решаем полученное уравнение:
4) Подставляем значение x = 5 в первое уравнение; имеем: 40 — 3y = 46; — 3y = 46 – 40; — 3y = 6. Отсюда
Способ сложения и вычитания следует предпочесть другим способам:
1) когда в данных уравнениях абсолютные величины коэффициентов при одном из неизвестных равны (тогда первый из этапов решения становится ненужным);
2) когда сразу видно, что числовые коэффициенты при одном из неизвестных уравниваются с помощью небольших целочисленных множителей;
3) когда коэффициенты уравнений содержат буквенные выражения.
Пример. Решить систему:
(a + c)x – (a – с)y = 2ab, (a + b)x – (a — b)y = 2ac.
1) Уравниваем коэффициенты при х, помножая обе части первого уравнения на (a + b), а второго на (а + с), получаем:
(a + c)(a +b)x – (a + b)(a — c)y = 2ab(a + b), (a +c)(a +b)x – (a-b)(a + c)y = 2ac(a +c).
2) Вычитаем из первого уравнения второе; получаем:
[(a — b)(a + c) – (a + b)(a — c)]y = 2ab(a + b) – 2ac(a + c).
3) Решаем полученное уравнение:
Это выражение можно значительно упростить, для чего однако, потребуются довольно долгие преобразования. В числителе и знаменателе раскроем скобки,
4) Чтобы найти x, уравняем коэффициенты при y в исходных уравнениях, помножив первое на (a — b), второе на (a — с). Вычтя одно полученное уравнение из другого, решим уравнение с одним неизвестным; найдем:
Выполняя такие же преобразования, как в предыдущем пункте, получим х = b + c — a. Подстановка значения y d одно из исходных уравнений потребовала бы более утомительных вычислений; при решении буквенных уравнений так бывает очень часто.
Системы линейных уравнений
 Линейные уравнения (уравнения первой степени) с двумя неизвестными Линейные уравнения (уравнения первой степени) с двумя неизвестными |
 Системы из двух линейных уравнений с двумя неизвестными Системы из двух линейных уравнений с двумя неизвестными |
 Системы из трех линейных уравнений с тремя неизвестными Системы из трех линейных уравнений с тремя неизвестными |
Линейные уравнения (уравнения первой степени) с двумя неизвестными
Определение 1 . Линейным уравнением (уравнением первой степени) с двумя неизвестными x и y называют уравнение, имеющее вид
| ax +by = c , | (1) |
где a , b , c – заданные числа.
Определение 2 . Решением уравнения (1) называют пару чисел (x ; y) , для которых формула (1) является верным равенством.
Пример 1 . Найти решение уравнения
| 2x +3y = 10 | (2) |
Решение . Выразим из равенства (2) переменную y через переменную x :
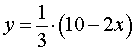 | (3) |
Из формулы (3) следует, что решениями уравнения (2) служат все пары чисел вида
где x – любое число.
Замечание . Как видно из решения примера 1, уравнение (2) имеет бесконечно много решений. Однако важно отметить, что не любая пара чисел (x ; y) является решением этого уравнения. Для того, чтобы получить какое-нибудь решение уравнения (2), число x можно взять любым, а число y после этого вычислить по формуле (3).
Системы из двух линейных уравнений с двумя неизвестными
Определение 3 . Системой из двух линейных уравнений с двумя неизвестными x и y называют систему уравнений, имеющую вид
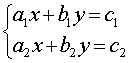 | (4) |
Определение 4 . В системе уравнений (4) числа a1 , b1 , a2 , b2 называют коэффициентами при неизвестных , а числа c1 , c2 – свободными членами .
Определение 5 . Решением системы уравнений (4) называют пару чисел (x ; y) , являющуюся решением как одного, так и другого уравнения системы (4).
Определение 6 . Две системы уравнений называют равносильными (эквивалентными) , если все решения первой системы уравнений являются решениями второй системы, и все решения второй системы являются решениями первой системы.
Равносильность систем уравнений обозначают, используя символ «
Системы линейных уравнений решают с помощью метода последовательного исключения неизвестных , который мы проиллюстрируем на примерах.
Пример 2 . Решить систему уравнений
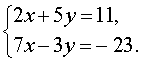 | (5) |
Решение . Для того, чтобы решить систему (5) исключим из второго уравнения системы неизвестное х .
С этой целью сначала преобразуем систему (5) к виду, в котором коэффициенты при неизвестном x в первом и втором уравнениях системы станут одинаковыми.
Если первое уравнение системы (5) умножить на коэффициент, стоящий при x во втором уравнении (число 7 ), а второе уравнение умножить на коэффициент, стоящий при x в первом уравнении (число 2 ), то система (5) примет вид
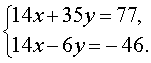 | (6) |
Теперь совершим над системой (6) следующие преобразования:
- первое уравнение системы оставим без изменений;
- из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.
В результате система (6) преобразуется в равносильную ей систему
Из второго уравнения находим y = 3 , и, подставив это значение в первое уравнение, получаем
Пример 3 . Найти все значения параметра p , при которых система уравнений
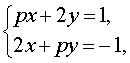 | (7) |
а) имеет единственное решение;
б) имеет бесконечно много решений;
в) не имеет решений.
Решение . Выражая x через y из второго уравнения системы (7) и подставляя полученное выражение вместо x в первое уравнение системы (7), получим
Следовательно, система (7) равносильна системе
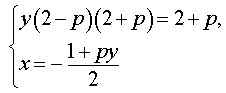 | (8) |
Исследуем решения системы (8) в зависимости от значений параметра p . Для этого сначала рассмотрим первое уравнение системы (8):
| y (2 – p) (2 + p) = 2 + p | (9) |
Если 
Следовательно, система (8) равносильна системе
Таким образом, в случае, когда 
Если p = – 2 , то уравнение (9) принимает вид
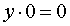
и его решением является любое число 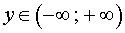
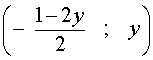
где y – любое число.
Если p = 2 , то уравнение (9) принимает вид
и решений не имеет, откуда вытекает, что и система (7) решений не имеет.
Системы из трех линейных уравнений с тремя неизвестными
Определение 7 . Системой из трех линейных уравнений с тремя неизвестными x , y и z называют систему уравнений, имеющую вид
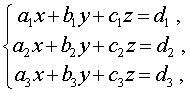 | (10) |
Определение 9 . Решением системы уравнений (10) называют тройку чисел (x ; y ; z) , при подстановке которых в каждое из трех уравнений системы (10) получается верное равенство.
Пример 4 . Решить систему уравнений
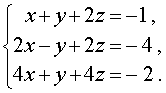 | (11) |
Решение . Будем решать систему (11) при помощи метода последовательного исключения неизвестных .
Для этого сначала исключим из второго и третьего уравнений системы неизвестное y , совершив над системой (11) следующие преобразования:
- первое уравнение системы оставим без изменений;
- ко второму уравнению прибавим первое уравнение и заменим второе уравнение системы на полученную сумму;
- из третьего уравнения вычтем первое уравнение и заменим третье уравнение системы на полученную разность.
В результате система (11) преобразуется в равносильную ей систему
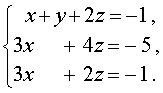 | (12) |
Теперь исключим из третьего уравнения системы неизвестное x , совершив над системой (12) следующие преобразования:
- первое и второе уравнения системы оставим без изменений;
- из третьего уравнения вычтем второе уравнение и заменим третье уравнение системы на полученную разность.
В результате система (12) преобразуется в равносильную ей систему
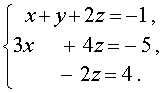 | (13) |
Из системы (13) последовательно находим
Пример 5 . Решить систему уравнений
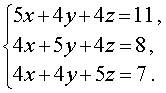 | (14) |
Решение . Заметим, что из данной системы можно получить удобное следствие, сложив все три уравнения системы:
Если числа (x ; y ; z) являются решением системы (14), то они должны удовлетворять и уравнению (15). Однако в таком случае числа (x ; y ; z) должны также быть решением системы, которая получается, если из каждого уравнения системы (14) вычесть уравнение (15):
Поскольку мы использовали следствие из системы (14), не задумываясь о том, являются ли сделанные преобразования системы (14) равносильными, то полученный результат нужно проверить. Подставив тройку чисел (3 ; 0 ; –1) в исходную систему (14), убеждаемся, что числа (3 ; 0 ; –1) действительно являются ее решением.
Замечание . Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы с нелинейными уравнениями» и нашим учебным пособием «Системы уравнений».
Система из двух уравнений первой степени
Система уравнений с двумя переменными. Уравнения первой степени. Способы решения
Уравнение может содержать не одну, а две переменных. Понятно, что такие уравнения называются уравнениями с двумя переменными.
Система уравнений – это два и более уравнений, которыми можно манипулировать для нахождения общих решений. Система из двух уравнений вкючает в себя две переменных, значения которых являются общими для обоих уравнений. С помощью одного уравнения системы решается другое, а в итоге решаются оба уравнения системы.
Способы решения системы уравнений первой степени.
1. Решение методом подстановки.
Суть в том, что в системе уравнений выбираете наиболее простое, в котором одну переменную выражаете через другую. Результат подставляете во второе уравнение, благодаря чему преобразуете его в более простое уравнение с одной переменной. Вычисляете это уравнение и получаете значение одной из переменных. Подставляется его в первое уравнение и получаете значение второй переменной. Так вы решаете всю систему уравнений.
Пример : Решим систему уравнений
│x + y = 1
│2x – y = 2
Первое уравнение системы проще второго – его и используем.
Выразим в нем x через у:
Подставляем это значение x в наше второе уравнение и находим значение y:
Мы получили значение y. Подставляем его в наше первое уравнение и находим теперь уже значение x:
Мы нашли значения обеих переменных.
2. Решение методом сложения.
Этот метод целесообразно применять, если при сложении одно из неизвестных пропадает.
Пример 1 : Решим систему уравнений
Сложим (вычтем) почленно оба уравнения системы:
│(x + y) + (x – y) = 5 + 1
│(x + y) – (x – y) = 5 – 1
Раскрываем скобки в обоих уравнениях и сводим подобные члены. В результате в первом уравнении пропадает у, во втором х. Мы получаем уравнения с одной переменной, которые проще решать:
│ x + y + x – y = 6
│ x + y – x + y = 4
Необязательно производить взаимное сложение и вычитание двух уравнений системы. Часто достаточно бывает произвести одно из двух действий, чтобы вычислить значение одной из двух переменных. А зная одну переменную, мы уже легко сможем найти и вторую.
Пример 2 . Решить систему уравнений
│2х + 4у = 26
│8х + 4у = 44
В обоих уравнениях есть число 4у. Значит, можем применить метод сложения. При этом произвести не взаимное сложение, а совершить лишь одно действие: вычесть из первого уравнения второе, чтобы 4у исчезло и чтобы в результате мы получили уравнение с одной переменной:
2х + 4у – 8х – 4у = 26 – 44.
Теперь можем найти и значение у, подставив значение х в любое из двух уравнений системы:
Ответ : х = 3, у = 5.
Однако рассмотрим еще один пример.
Пример 3 : Решим систему уравнений
│3х + 5у = 21
│8х – 3у = 7
Здесь нет переменных с одинаковыми коэффициентами, чтобы при вычитании они исчезли. Что делать в этом случае? Для таких случаев придумано оригинальное решение: умножим почленно первое уравнение на 3, а второе на 5. От этого истина не пострадает, потому что мы просто получим равносильные уравнения. Зато благодаря этому приему у нас появятся одинаковые переменные 15у:
│(3х + 5у = 21) · 3
│(8х – 3у = 7) · 5
│3 · 3х + 3 · 5у = 3 · 21
│5 · 8х – 5 · 3у = 5 · 7
│9х + 15у = 63
│40х – 15у = 35
Итак, у нас появились одинаковые переменные и мы можем сложить два уравнения, чтобы прийти к уравнению с одной переменной:
9х + 15у + 40х – 15у = 63 + 35
Осталось найти значение второй переменной, подставив значение х, например, в первое уравнение системы:
Ответ : х = 2; у = 3.
Опять же не всегда нужно преобразовывать оба уравнения системы так, как было в предыдущем примере. Бывает и так, что достаточно изменить лишь одно из уравнений.
Пример 4 . Решим систему уравнений:
│3х – 4у = 7
│х + 3у = 11
Здесь достаточно второе уравнение умножить на –3. Тогда мы получим число –3х, а при сложении двух уравнений придем к уравнению с одной переменной.
Итак, умножаем второе уравнение на –3:
Теперь складываем два уравнения, приходим к уравнению с одной переменной у и решаем его:
3х – 4у –3х – 9у = 7 – 33
И находим значение х. Это проще сделать во втором уравнении:
Ответ : х = 5; у = 2.
3. Решение методом введения новой переменной.
Пример . Решить систему уравнений
│ 2 3
│———— + ———— = 2
│ х – 3у 2х + у
│
│ 8 9
│———— – ———— = 1
│ х – 3у 2х + у
Перед нами система сложных уравнений, осложненных дробными числами. Наша задача – упростить их, чтобы потом решить. Если применить какой-нибудь из первых двух методов, получатся еще более сложные уравнения. Зато хорошо подходит метод введения новой переменной, благодаря которому мы целую дробь можем заменить одной переменной. Как это сделать?
Обратите внимание: у первых чисел обоих уравнений одинаковые знаменатели х – 3у, при этом их числители делятся на 2. У вторых чисел тоже одинаковые знаменатели 2х + у, а их числители делятся на 3. Этим и воспользуемся.
1) Выпишем снова нашу систему уравнений, разложив на множители числители второго уравнения и вынеся их за дробь:
│ 2 3
│———— + ———— = 2
│ х – 3у 2х + у
│
│ 2 3
│4 · ———— – 3 · ———— = 1
│ х – 3у 2х + у
Теперь в обоих уравнениях у нас абсолютно одинаковые первые дроби и абсолютно одинаковые вторые дроби.
2) Заменим эти дроби новыми переменными a и b следующим образом:
Так мы существенно упрощаем уравнения, которые обретают совсем иной вид:
3) Применяем уже известный нам метод подстановки.
Первое уравнение проще, поэтому сначала выражаем в нем а через b:
Подставляем полученное значение а во второе уравнение, раскрываем скобки, приводим подобные члены и вычисляем численное значение b:
Раз нам известно численное значение b, то мы легко можем найти и численное значение а. Это проще сделать с помощью первого уравнения:
Вписываем в дроби эти значения а и b:
4) Преобразуем эти уравнения по известному вам правилу: неизвестные влево, известные вправо:
│ х – 3у = 2 : 1
│2х + у = 3 : 1
│ х – 3у = 2
│2х + у = 3
5) Решаем эту систему уравнений снова с помощью метода подстановки. Для этого в первом уравнении х выражаем через у:
Подставляем во второе уравнение и находим у:
И с помощью первого уравнения находим х:
Мы нашли значения х и у в нашей исходной системе уравнений – а значит, решили ее.
Ответ : х = 11/7, у = –1/7
Как видно из этого примера, нередки случаи, когда при решении системы уравнений надо последовательно применить сразу несколько методов.
http://www.resolventa.ru/spr/algebra/system.htm
http://raal100.narod.ru/index/0-250