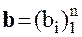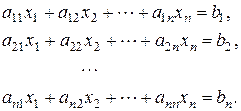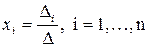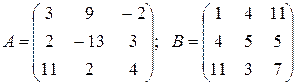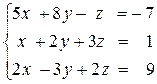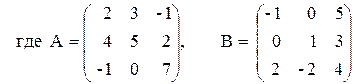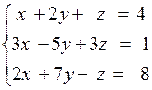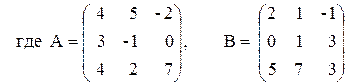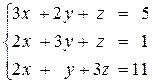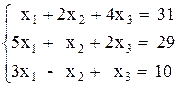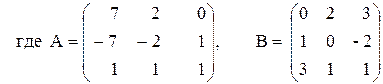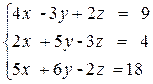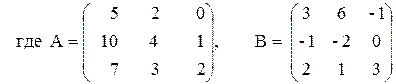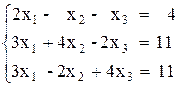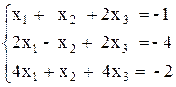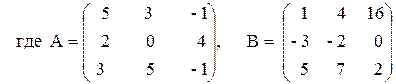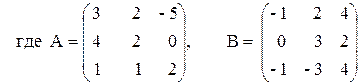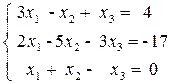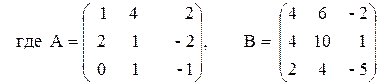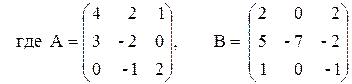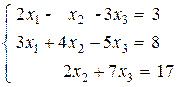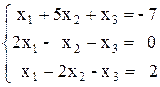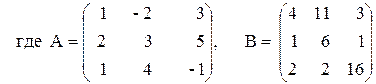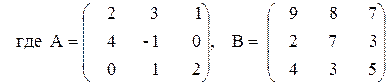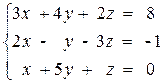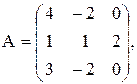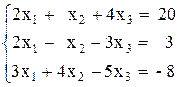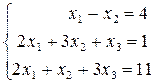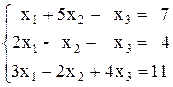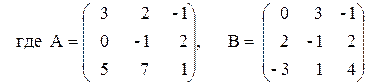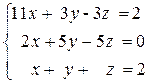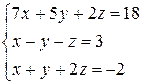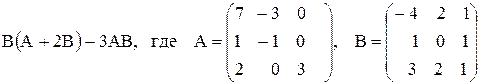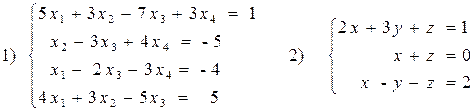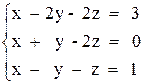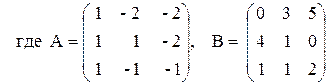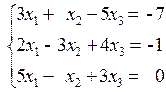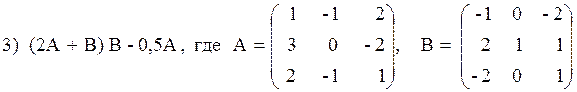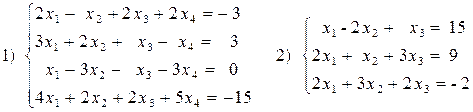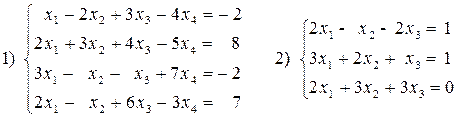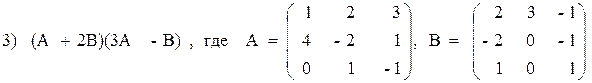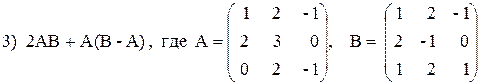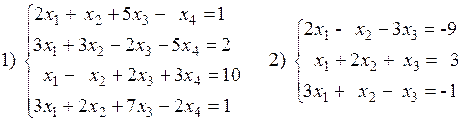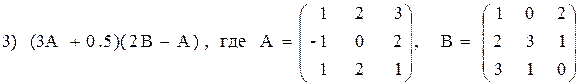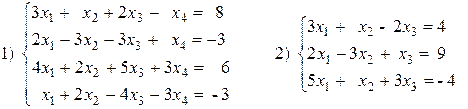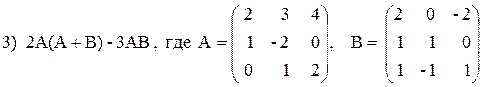Решение систем линейных алгебраических уравнений
Страницы работы
Содержание работы
Лабораторная работа №3
Решение систем линейных алгебраических уравнений
Практика использования итерационных методов решения системы линейных алгебраических уравнений. Сравнительный анализ методов.
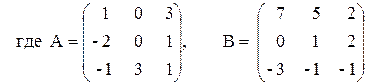
Решить систему линейных алгебраических уравнений (САУ)
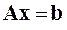
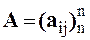
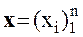
итерационными методами Зейделя и наискорейшего спуска с точностью до e = 0,001. Для сравнения с истинными значениями корней выполнить решение указанной САУ методом Гаусса.
Общий вид алгоритма Зейделя и наискорейшего спуска
Метод Зейделя заключается в том, что найденное на 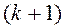
Расчетные соотношения метода Зейделя для подготовленной системы уравнений (4.13) имеют вид
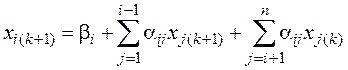
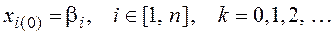
При составлении программы для вычислений на ЭВМ вместо соотношения (4.18) удобнее использовать выражение, в котором фигурируют элементы исходной системы уравнений
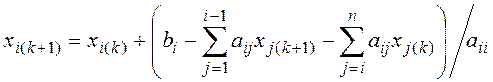
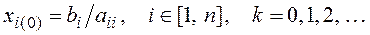
Если матрица 
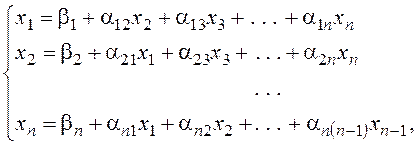
где 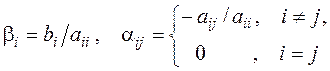


Из неособенной матрицы 

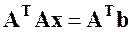
Метод наискорейшего спуска. Данный метод относится к группе нелинейных градиентных алгоритмов. Градиентные алгоритмы, уточнение решения в которых осуществлялось по отдельным координатам, предполагают траекторию движения к истинному решению сразу по всем координатам по линии наискорейшего спуска в направлении, противоположном вектору градиента функционала, связанного с ошибкой между истинным решением и решением на 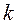
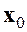
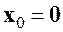
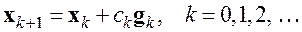
где 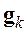
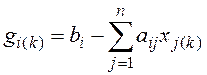
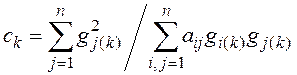
Чтобы упростить процедуру определения вектора невязки, особенно при больших порядках 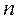
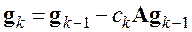
Однако из-за наличия вычислительных погрешностей векторы 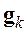
Если матрица 
SUBROUTINE N1YMGS (A,B,N,G,X),
SUBROUTINE N1YMNS (A,B,N,G,X)
реализуют алгоритмы решения САУ методами Зейделя и наискорейшего спуска (одна итерация) соответственно.
Входные параметры подпрограмм:
А(N,N) — (N ´ N)-мерная матрица САУ;
B(N) — N-мерный вектор правой части САУ;
N — мерность САУ;
G(N) — N-мерный вектор невязки (g = b — Ax);
X(N) — N-мерный вектор начальных условий решения САУ.
Выходные параметры подпрограммы:
X(N) — N-мерный вектор уточненных значений решения САУ.
Окончание итерационной процедуры производиться при выполнении условия 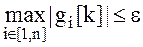
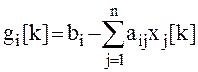
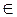
SUBROUTINE N1YGAU (A,B,X,N)
реализует алгоритм метода Гаусса с выбором главного элемента.
Входные A, B, N и выходной X параметры подпрограммы N1YGAU совпадают по описанию с аналогичными параметрами в подпрограммах N1YMGS, N1YMNS.
В подпрограмме N1YGAU матрица A приводится к треугольной.
Решение систем линейных алгебраических уравнений (СЛАУ)
ЛАБОРАТОРНАЯ РАБОТА № 3
Тема: Решение систем линейных уравнений, работа с матрицами
Цель работы: Изучение возможностей пакета Ms Excel при решении задач линейной алгебры. Приобретение навыков решения систем линейных алгебраических уравнений и выполнение действий над матрицами средствами пакета.
Предварительно вспомним некоторые сведения из курса высшей математики, необходимые для выполнения данной лабораторной работы.
Решение систем линейных алгебраических уравнений (СЛАУ).
Пусть задана СЛАУ следующего вида:
Эту систему можно представить в матричном виде: AX=b, где

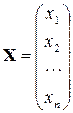
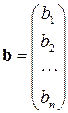
При выполнении лабораторной работы систему линейных алгебраических уравнений необходимо будет решать методом обратной матрицы и методом Крамера. Вспомним основные формулы, используемые в этих методах.
Метод обратной матрицы.
Систему линейных алгебраических уравнений Ax=b умножим слева на матрицу, обратную к А. Система уравнений примет вид:
A -1. A . x=A -1. b, E . x=A -1. b,(E – единичная матрица)
Таким образом, вектор неизвестных вычисляется по формуле x=A -1. b.
В этом случае неизвестные x1,x2,…, xn вычисляются по формуле:
где D – определитель матрицы A, Di – определитель матрицы, получаемой из матрицы А путем замены i-го столбца вектором b.
Обратите внимание на особенность работы с матричными формулами: необходимо предварительно выделять область, в которой будет храниться результат, а после получения результата преобразовывать его к матричному виду, нажав клавиши F2 и Ctrl+Shift+Enter.
Теперь рассмотрим решение системы линейных уравнений методом обратной матрицы и методом Крамера на следующих примерах.
ПРИМЕР 3.1. Решить систему методом обратной матрицы:
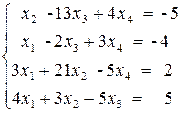
В этом случае матрица коэффициентов А и вектор свободных коэффициентов b имеют вид:
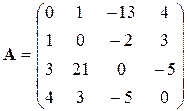
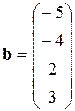
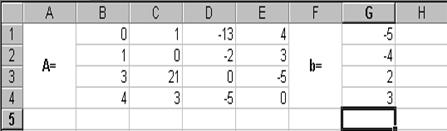
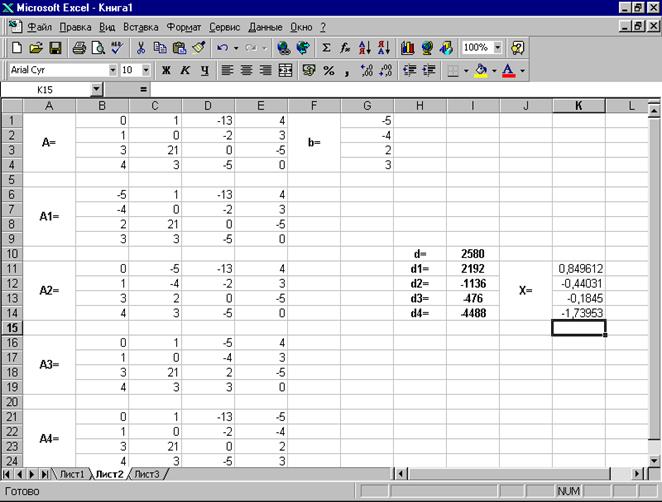
Введём матрицу A и вектор b в рабочий лист MS Excel (рис. 3.1).
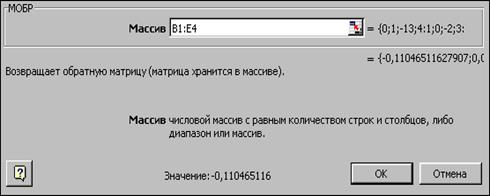
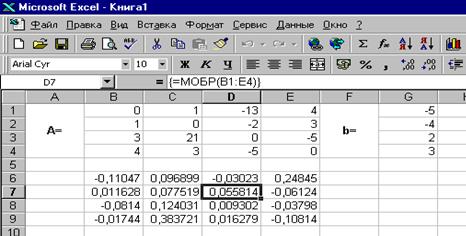
В нашем случае матрица А находится в ячейках B1:Е4, а вектор b в диапазоне G1:G4. Для решения системы методом обратной матрицы необходимо вычислить матрицу, обратную к A. Для этого выделим ячейки для хранения обратной матрицы (это нужно сделать обязательно. ); пусть в нашем случае это будут ячейки B6:E9. Теперь обратимся к мастеру функций, и в категории Математические выберем функцию МОБР,предназначенную для вычисления обратной матрицы (рис. 3.2), щелкнув по кнопке OK, перейдём ко второму шагу мастера функций. В диалоговом окне, появляющемся на втором шаге мастера функций, необходимо заполнить поле ввода Массив(рис. 3.3). Это поле должно содержать диапазон ячеек, в котором хранится исходная матрица — в нашем случае B1:E4. Данные в поле ввода Массив можно ввести, используя клавиатуру или выделив их на рабочем листе, удерживая левую кнопку мыши.
Если поле Массив заполнено, можно нажать кнопку OK. В первой ячейке, выделенного под обратную матрицу диапазона, появится некое число. Для того чтобы получить всю обратную матрицу, необходимо нажать клавишу F2 для перехода в режим редактирования, а затем одновременно клавиши Ctrl+Shift+Enter. В нашем случае рабочая книга MS Excel примет вид изображенный на рис. 3.4.
Теперь необходимо умножить полученную обратную матрицу на вектор b. Выделим ячейки для хранения результирующего вектора, например H6:H9. Обратимся к мастеру функций, и в категории Математические выберем функцию МУМНОЖ,которая предназначена для умножения матриц. Напомним, что умножение матриц происходит по правилу строка на столбец и матрицу А можно умножить на матрицу В только в том случае, если количество столбцов матрицы А равно количеству строк матрицы В. Кроме того, при умножении матриц важен порядок сомножителей, т.е. АВ≠ВА
Перейдём ко второму шагу мастера функций. Появившееся диалоговое окно (рис. 3.5) содержит два поля ввода Массив1 и Массив2. В поле Массив1 необходимо ввести диапазон ячеек, в котором содержится первая из перемножаемых матриц, в нашем случае B6:E9 (обратная матрица), а в поле Массив2 ячейки, содержащие вторую матрицу, в нашем случае G1:G4 (вектор b).
Если поля ввода заполнены, можно нажать кнопку OK. В первой ячейке выделенного диапазона появится соответствующее число результирующего вектора. Для того чтобы получить весь вектор, необходимо нажать клавишу F2, а затем одновременно клавиши Ctrl+Shift+Enter. В нашем случае результаты вычислений (вектор х), находится в ячейках H6:H9.
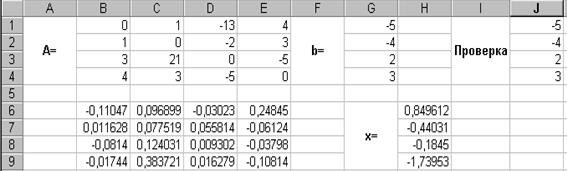
Для того чтобы проверить, правильно ли решена система уравнений, необходимо умножить матрицу A на вектор xиполучить в результате вектор b. Умножение матрицы A на вектор x осуществляется при помощи функции МУМНОЖ(В1:Е4;Н6:Н9), так как было описанной выше.
В результате проведенных вычислений рабочий лист примет вид изображенный на рис. 3.6.
ПРИМЕР 3.2. Решить систему из ПРИМЕРА 3.1 методом Крамера.
Введём матрицу А и вектор b на рабочий лист. Кроме того, сформируем четыре вспомогательные матрицы, заменяя последовательно столбцы матрицы A на столбец вектора b (рис. 3.7).
Для дальнейшего решения необходимо вычислить определитель матрицы A. Установим курсор в ячейку I10 и обратимся к мастеру функций. В категории Математические выберем функцию МОПРЕД,предназначенную длявычисления определителя матрицы, и перейдём ко второму шагу мастера функций. Диалоговое окно, появляющееся на втором шаге содержит поле ввода Массив.В этом поле указывают диапазон матрицы, определитель которой вычисляют. В нашем случаеэтоячейки B1:E4.
Для вычисления вспомогательных определителей введем формулы:
В результате в ячейке I10 хранится главный определитель, а в ячейках I11:I14 – вспомогательные.
Воспользуемся формулами Крамера и разделим последовательно вспомогательные определители на главный. В ячейку K11 введём формулу =I11/$I$10. Затем скопируем её содержимое в ячейки K12, K13 и K14. Система решена.
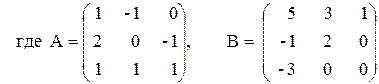
ПРИМЕР 3.3. Вычислить матрицу С по формуле: C=A 2 +2AB, где
Введем исходные данные на рабочий лист (рис. 3.8).
Для умножения матрицы А на матрицу В, выделим диапазон B5:D7ивоспользуемся функцией МУМНОЖ(B1:D3;G1:I3).
Результат вычисления A 2 =A*Aпоместим в ячейкиG5:I7,воспользовавшисьформулой МУМНОЖ(B1:D3;B1:D3).
Умножение (деление) матрицы на число можно выполнить при помощи элементарных операций. В нашем случае необходимо умножить матрицу из диапазона B5:D7начисло 2. Выделим ячейки B9:D11 и введем формулу =2*B5:D7.
Сложение (вычитание) матриц выполняется аналогично. Например, выделим диапазон G9:I11 и введем формул =B9:D11+ G5:I7.
Для получения результата в обоих случаях необходимо нажать комбинацию клавиш Ctrl+Shift+Enter.
Кроме того, в строке формул рабочего листа, изображенного на рис. 3.8, показано как можно вычислить матрицу Содним выражением.
ВАРИАНТЫ З А Д А Н И Й
1. Решить систему уравнений методом Крамера.
2. Решить систему уравнений с помощью обратной матрицы.
3. Выполнить действия над матрицами.
При решении систем обязательно выполнить проверку.
Вариант №1 1) 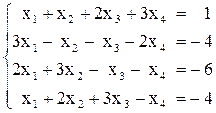
3) 2 (A + B) (2B – A),
Вариант №2 1) 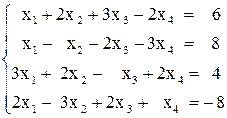
3) 3 A — (A + 2B) B,
Вариант № 3 1) 
3) 2(A–B)(A 2 + B),
Вариант №4 1) 
3) (A 2 – B 2 )(A + B),
Вариант №5 1) 
3) (A–B 2 )(2A+B),
Вариант №6 1) 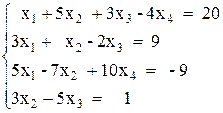
3) (A – B) A + 2B,
Вариант №7 1) 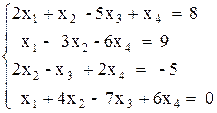
3) 2(A–0,5B)+AB,
Вариант №8 1) 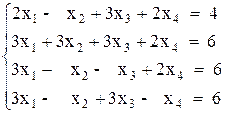
3) (A – B)A + 3B,
Вариант №9 1) 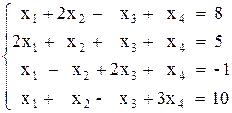
3) 2A – (A 2 + B) B,
Вариант №10 1) 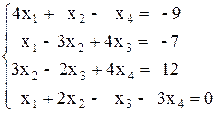
3) 3 (A 2 – B 2 ) –2АB,
Вариант №11 1) 
3) (2A–B)(3А+B)–2АВ,
Вариант №12 1) 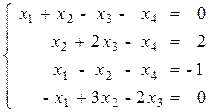
3) А(A 2 –B)-2(B+А)В,
Вариант №13 1) 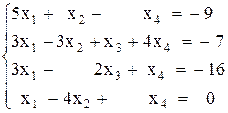
3) (A+B)A–B(2А+3В),
Вариант №14 1) 
3) A(2A+B)–B(А–В),
Вариант №15 1) 
3) 3(A+B)(AВ–2А),
Вариант №16 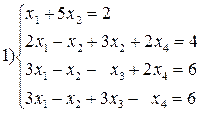
3) 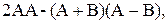
Вариант №17 1) 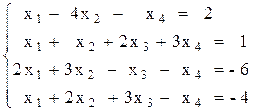
3) 2А + 3B(АB-2А),
Вариант №18 1) 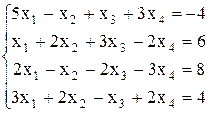
3)
Вариант №191) 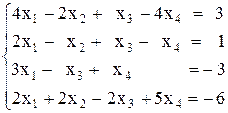
3) 2A — АB(В — А) + В,
Вариант №20 1) 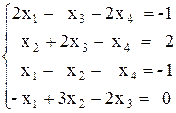
3) A 2 — (A + B)–(А – 3В),
Вариант №21 1) 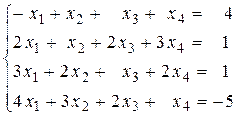
3)
Вариант№22

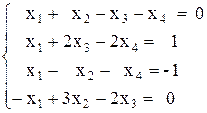
3) А(A — B) + 2В(A + В),
Вариант№24 1) 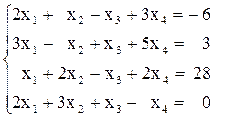
Вариант№25
Вариант №26
Вариант №27
Вариант №28
Вариант№29
Вариант №30
Решение системы линейных алгебраических уравнений
Главная > Решение
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
Лабораторная работа 3. Решение системы линейных алгебраических уравнений
Цель: Освоить технологию решения систем линейных алгебраических уравнений в интегрированной среде MathCad.
Задание: Решить систему линейных алгебраических уравнений
используя функцию lsolve;
методом простой итерации;
Методика выполнения задания:
Чтобы решить систему линейных алгебраических уравнений можно использовать несколько способов, причем технология нахождения параметров заданной системы линейных алгебраических уравнений на первых этапах аналогична, а именно, пусть задана система трех линейных алгебраических уравнений с тремя неизвестными, найдем ее решение. Для этого присвоим некоторой переменной М матрицу значений коэффициентов при неизвестных, воспользуемся динамической кнопкой 
Определение решения системы матричным методом .
Используем представление системы линейных алгебраических уравнений в векторной форме, то есть A*X=B, где A – матрица значений при неизвестных, B – вектор свободных членов, а Х – вектор неизвестных, тогда исходя из этого уравнения Х=A -1 *B, задав последнюю формулу получим решение системы линейных алгебраических уравнений.
Определение решения методом Гаусса.
Сформируем расширенную матрицу системы Mr добавлением к матрице М справа матрицу V, используя встроенную функцию augment . Приведем расширенную матрицу к ступенчатому виду Mg, с помощью функции rref и выделим из нее блок матрицы – ее последний столбец, содержащий решение системы, с помощью функции submatrix .
Определение решения системы с помощью встроенной функции lsolve .
Активизируем кнопку Мастер функций на панели инструментов Стандартная и в категории Solving выберем встроенную функцию lsolve (M, V);
Результаты решения заданной системы линейных алгебраических уравнений отображены на рис. ().
l
Рис. Пример решения системы линейных уравнений
4. Решение системы линейных алгебраических уравнений методом простой итераций .
Введем переменную ORIGIN = 1 для нумерации столбцов и строк матрицы с 1 (по умолчанию ORIGIN=0). Сформируем матрицы α и β эквивалентной системы х= β + αх.
Для описания i и j воспользуемся кнопкой 

Определим нормы матрицы α с помощью встроенных функций, используя кнопку 
Зададим начальное приближение, используя кнопку 
Вычислим 10 последовательных приближений и погрешности каждого из них.
Фрагмент рабочего документа MathCAD с соответствующими вычислениями приведен ниже на рис ().
Рис. Пример решения системы линейных уравнений методом простой итерации
5. Решение системы линейных уравнений методом Зейделя .
Сформируем матрицы α и β преобразованной системы х= β + α1х+ α2х и матрицу α= α1+ α2.
Фрагмент рабочего документа MathCAD с соответствующими вычислениями по методу Зейделя приведен ниже на рис ().
Рис. Пример решения системы линейных уравнений методом Зейделя
http://lektsii.org/6-107067.html
http://gigabaza.ru/doc/113527.html