Система линейных уравнений над полем вычетов

Вычисления в полях вычетов

Рассмотрим некоторые особенности вычислений в полях вычетов. Найдем, например, определитель 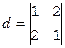, элементы которого суть вычеты из поля
(Z₃, +₃, ×₃). Если действовать «по науке», надо писать

Можно, однако, поступить проще. Будем считать элементы определителя обычными целыми числами из кольца Z, тогда d=1×1–2×2= –3.

Как найти для целого числа из Z соответствующий вычет из Z_n? Для этого надо к числу прибавить (или отнять от него) величину, кратную n, чтобы результат принадлежал множеству вычетов Z_n=<0,1,¼,n–1>. В данном случае прибавим 3 и получим –3+3=0 – тот же результат.

В дальнейшем станем действовать аналогично, к тому же не будем педантично ставить индекс +_n, ×_n около символов операций, обозначая их просто + и
× , если значение индекса n ясно из контекста.

Рассмотрим решение системы линейных уравнений над полем вычетов.

Пример. Решим над тремя полями: Q, Z₃, Z₅ систему уравнений A×X=B, где . т.е.

Заметим, что коэффициенты системы (0, 1 и 2), включая свободные члены, можно рассматривать не только как числа (т.е. элементы поля Q), но и как элементы интересующих нас конечных полей Z₃ и Z₅. В противном случае постановку задачи пришлось бы как-то изменять.

Решать систему будем по правилу Крамера. Вычислим над полем Q четыре опре­делителя:

.

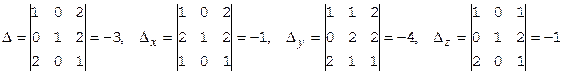
Значения неизвестных найдем по формулам Крамера: .

Приведем значения определителей в поле вычетов Z₃=<0,1,2>, получим: D=0, D_x=2, D_y=2, D_z=2. Видим, что над этим полем система несовместна.

Приведем значения определителей в поле вычетов Z₅=<0,1,2,3,4>: D=2, D_x=4, D_y=1, D_z=4. Значения неизвестных снова найдем по формулам Крамера: . Как понимать найденное значение неизвестной ? Дробь не является элементом поля Z₅, поэтому ее надо рассматривать как выражение, которое необходимо вычислить согласно правилам действий в этом поле: (поскольку произведение 2×3=6, а 6 в поле Z₅ переходит в 1). Итак, решение системы уравнений над полем Z₅ таково: x=2, y=3, z=2.

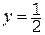
Сделаем проверку (символом Þ обозна­чен переход от целых чисел к вычетам по модулю 5). Первое уравнение: 1×2+2×2=6 Þ 1, второе уравнение: 1×3+2×2=7 Þ 2, третье уравнение: 2×2+1×2=6 Þ 1. Видим, что найден­ные значения вычетов удовлетворяют сис­теме уравнений над полем Z₅.

Решим ту же систему над полем Z₃ методом Гаусса. Составим расширенную матрицу: . Если бы мы решали систему над полем рациональных чисел Q, то первым шагом выполнили бы операцию (3)–2×(1). В поле Z₃ коэффициенту –2 соответствует вычет 1, поэтому выполним операцию (3)+1×(1). В 1-ом столбце имеем 2+1×1=3Þ0, во 2-ом столбце сохранится 0, в третьем столбце 1+1×2=3Þ0, в столбце свободных членов 1+1×1=2, так что . В алгебраической форме 3-е уравнение этой системы имеет вид 0×x+0×y+0×z=2. Очевидно, что оно не имеет решения, поэтому система над полем Z₃ несовместна.

Найдем решение той же системы над полем Z₅ методом Гаусса. Вместо операции (3)–2×(1), с которой начинается решение этой системы над полем рациональных чисел Q, выполним операцию (3)+3×(1), поскольку в поле Z₅ коэффициенту –2 соответствует вычет 3. В 1-ом столбце получим 2+3×1=5Þ0, во 2-ом столбце сохранится 0, в третьем, в 3-ем столбце имеем 1+3×2=7Þ2, в столбце свободных членов 1+3×1=4. Таким образом, получим . 3-ю строку этой матрицы можно сократить (разделить) на 2: .

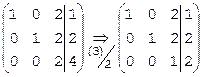
Теперь выполним операции (1)+3×(3) и (2)+3×(3) – в 1-й и во 2-й строках 3-го столбца получится 2+3×1=5Þ0, остальные элементы этих строк сохраняться: .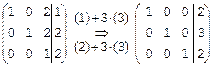

Видим, что получилось решение, ранее найденное по правилу Крамера: x=2, y=3, z=2.

Системы линейных уравнений над полем.

Рассмотрим один из наиболее распространенных на практике методов решения систем линейных уравнений над полем_; называемый методом Гаусса.

Пусть дана система уравнений над произвольным полем. Если А = Оmхn, то система совместна только при β ↓ = 0 ↓ . При выполнении этого условия любой вектор из Р ( n ) является ее решением. Далее считаем, что А — ненулевая матрица. Приведем расширенную матрицу В = (А,β ↓ ) к специальному ступенчатому виду с помощью элементарных преобразований строк. Пусть при этом получилась матрица С = (с_ij)_mx(n+1)типа S(i₁. i_r). Тогда система равносильна системе уравнений

где С’ = (с_ij)_mхn,a γ ↓ —последний столбец матрицы С. В зависимости от значений параметров r,i₁. i_r возможны следующие три принци­пиально различных случая.

1) i_r = п + 1. В этом случае столбец β ↓ матрицы В не выражается линейно через столбцы матрицы А, и система уравнений несовместна.

2) i_r ≤ n,r= п.В этом случае матрица С имеет тип S(1,2. n), а тогда имеем:β ↓ = A₁ ↓ c_{1 n+1} + . + A_n ↓ c_nn+1 и система столбцов A₁ ↓ , . , A_n ↓ линейно независима. Отсюда и следует, что столбецγ ↓ является единственным решением системы уравнений . Следовательно, в рассматриваемом случае система совместна и определенна.

которая, очевидно, равносильна системе (1), Подставляя в (3) вместо х_ir+1. x_iппроизвольные элементы air+l , . , a_inполя P, мы однозначно определим значения а_i1. а_ir остальных неизвестных x_i1. x_ir так, что набор (a₁. ,a_n) будет решением системы (3). Нетрудно заметить, что каждое решение системы (3) можно получить указанным способом. Так как r ↓ ), можно сделать следующий вывод. При решении системы уравнений методом Гаусса логически возможны следующие взаимно исключающие случаи:

1) rangA ≠rangВ, система несовместна;

2) rangА = rangВ= п, система совместна и определенна;

Эту теорему называют теоремой Кронекера-Капеллив честь немецкого математика Л. Кронекера (1823—1891) и итальянского математика А. Капелли (1855-1910).

Пояснение. Система уравнений Ax=b разрешима тогда и только тогда, когда \operatorname A = \operatorname(A, b), где (A, b) — расширенная матрица, полученная из матрицы A приписыванием столбца b.

ДОК-ВО

Пусть система совместна. Тогда существуют числа x_1,\dots,x_n\in\mathbb R такие, что b=x_1 a_1+\dots+x_n a_n. Следовательно, столбец b является линейной комбинацией столбцов a_1,\dots,a_n матрицы A. Из того что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что \operatorname A = \operatorname B.

Пусть \operatorname A = \operatorname B = r. Возьмём в матрице A какой-нибудь базисный минор. Так как \operatorname B = r, то он же будет базисным минором и матрицы B. Тогда, согласно теореме о базисном миноре, последний столбец матрицы B будет линейной комбинацией базисных столбцов, то есть столбцов матрицы A. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы A.

Следствия

· Количество главных переменных системы равно рангу системы.

· Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.

Теорема (критерий определенности).Система линейных уравнении над полем имеет единственное решение тогда и только тогда,когда ранги основной и расширенной матриц системы равны числу её неизвестных.

Теорема.Совместная и неопределенная система линейных уравнений над полем Р имеет бесконечно много решений при бесконечном поле Р и q n — r решений при |Р| = q, где п — число неизвестных, аr — ранг основной (и расширенной) матрицы системы.

Рассмотрим еще метод решения систем линейных уравнений над полем, основанный на использовании ранговых подматриц матриц этих систем.

Пусть дана система с основной матрицей А и расширенной матрицей В = (A, β ↓ )и известно, что rangA = rangВ = r. Выберем в матрице А произвольную ранговую подматрицу

Так как rangB = r и А есть подматрица матрицы В, то А’ является ранговой подматрицей и для матрицы В, Отсюда и легко получить, что система строк является базисом системы всех строк матрицы В. Поэтому матрицу В элементарными преобразованиями строк можно привести к матрице вида:

Также равносильна системе уравнений

где β‘ ↓ — последний столбец матрицы B’, а А’ получена из В’ удалением столбца β‘ ↓ . Удалив из системы (4) последние m-r уравнений и перенеся в оставшихся уравнениях в правые части все слагаемые, не содержащие неизвестных x_j1, . , x_jrполучим систему из r уравнений, равносильную системе:

(5)

Подставив в (5) вместо x_jr+1, . , x_jnпроизвольные элементы из Р, мы получим систему rуравнений с r неизвестными x_j1, . x_jr, которая по теореме Крамера имеет единственное решение x_j1= a_j1, . x_jr= а_jr. В итоге мы найдем решение (a₁, . a_n) системы (5) . Легко видеть, что таким образом можно получить все решения системы (5). Действительно, если γ = (с₁, . ,c_n) — любое решение системы (5), то, заменив в (5) х_i на с_i при всех i Є 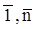,получим систему верных равенств, которая свидетельствует о том, что c_j1. c_jrесть решение системы, полученной из (5) заменой x_jr+1, . x_jnсоответственно элементами c_jr+1. c_jn.

Замечание 1. Вместо того чтобы решать методом Крамера все системы уравнений, получаемые из (5) заменой xjr+1, . , xjn всевозможными элементами поля Р, можно решить методом Крамера саму систему (5), считаяx_jr+1. x_jn параметрами со значениями из поля Р. В итоге неизвестные x_j1, . , x_jrбудут представлены в виде аффинных функций от переменных x_jr+1, . , x_jn. Придавая последним произвольные значения из Р и вычисляя соответствующие значения неизвестных x_j1. x_jrполучим все решения системы (5).

Замечание 2. Набор неизвестных x_jr+1, . x_jnиз правых частей уравнений системы (5) называют системой свободных неизвестных системы уравнений В общем случае система свободных неизвестных для системы находится неоднозначно, а определяется выбором ранговой подматрицы в матрице A.

3. Поле частных коммутативного кольца без делителей нуля. Простые поля. Расширения полей. Поле разложения многочлена. Конечные поля и их свойства

По́ле в общей алгебре — алгебра, для элементов которой определены операции сложения, вычитания, умножения и деления (кроме деления на нуль), причём свойства этих операций близки к свойствам обычных числовых операций. Простейшим полем является поле рациональных чисел (дробей). Хотя названия операций поля взяты из арифметики, следует иметь в виду, что элементы поля не обязательно являются числами, и определения операций могут быть далеки от арифметических.

По́лем называется множество F с двумя бинарными операциями + (аддитивная операция или сложение) и \cdot (мультипликативная операция или умножение), если оно (вместе с этими операциями) образует коммутативное ассоциативное кольцо c единицей, все ненулевые элементы которого обратимы.

Иными словами, множество F с двумя бинарными операциями + (сложение) и \cdot (умножение) называется полем, если оно образует коммутативную группу по сложению, все его ненулевые элементы образуют коммутативную группу по умножению, и выполняется свойство дистрибутивности.

Примеры полей

Числа вида a + b\sqrt<2>, a,b\in\ , относительно обычных операций сложения и умножения. Это один из примеров квадратичного поля, которое образует подполе в .

_p — поле вычетов по модулю p, где p — простое число.

_q — конечное поле из q=p^k элементов, где p — простое число, k — натуральное. Все конечные поля имеют такой вид.

(x) — поле рациональных функций вида f(x)/g(x), где f и g — многочлены над некоторым полем (при этом g \ne 0, а f и g не имеют общих делителей, кроме констант).

Определение. Элементы a и b кольца, для которых 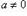, , но ab = 0, называются делителями нуля. Кольцо без делителей нуля называется также областью целостности.

Теорема 1. Из ab = ac следует b = c, если только и не является делителем нуля.

Доказательство. Из ab = ac следует ab — ac = 0 или a(b — c) = 0. Но так как 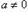и не делитель нуля, то b — c = 0, b = c.

В дальнейшем нам придется иметь дело исключительно с кольцами без делителей нуля. Для них из ab = ac и следует b = c.

При умножении справедливы обычные правила знаков, а именно:

Теорема 2. Поле не имеет делителя нуля, т. е. если ab = 0, то либо a = 0, либо b = 0.

Доказательство. Если ab = 0 и a ≠ 0, то, умножая обе части равенства на a -1 , найдем 1 · b = a -1 · 0, т. е. b = 0.

Итак, поле является кольцом без делителей нуля. Утверждение, обратное этому, вообще неверно: существуют кольца без делителей нуля (например, кольцо целых чисел), не являющиеся полями. Однако для конечных колец обратная теорема также верна. А именно:

Теорема 3. Всякое конечное кольцо без делителей нуля, содержащее более одного элемента, является полем.

Доказательство. Достаточно проверить свойство VII. Пусть a ≠ 0. Каждому элементу x кольца поставим в соответствие элемент y =ax. Если x₁ ≠ x₂, то также y₁ ≠ x_y, т. к. иначе ax₁ = ax₂ и x₁ = x₂(Теорема1).Значит, x → y есть взаимно однозначное отображение всего кольца R на некоторое его подмножество M, т. е. R

M. Но по основнай теореме о конечных множествах (Конечное множество не равномощно никакому его собственному подмножеству и собственному надмножеству) конечное множество R не равномощно своему собственному подмножеству. Поэтому R = M, т. е. для любого элемента 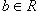существует в R элемент q такой, что q → b, т. е. aq = b, что и доказывает VII.

Так как все элементы поля, отличные от нуля, образуют по умножению коммутативную группу, то для любого элемента a ≠ 0 степень a n определена при любом целом показателе n.

Для частного элементов любого поля верны те же правила оперирования, что и для обыкновенных дробей.

Простые поля

Подполе. Простое поле. Множество M поля P называется подполем P, если оно само является полем при тех же операциях сложения и умножения, которые заданы в поле P. Тогда P называется надполем или расширением поля M.

Так, поле рациональных чисел является подполем поля действительных чисел, а последнее — подполем поля комплексных чисел.

Теорема 1. Для того чтобы множество M поля P, содержащее не менее двух элементов, было подполем, необходимо и достаточно, чтобы сумма, разность, произведение и частное (если только оно существует в P) любых элементов из M снова принадлежали к M.

Доказательство вполне аналогично проведенному для соответствующей теоремы о кольцах (теорема о кольцах: Для того чтобы непустое подмножество M кольца R было его подкольцом, необходимо и достаточно, чтобы сумма, разность и произведение любых двух элементов из M снова принадлежали M.).

Всякое подполе M поля P содержит 0 как разность a — a, где , и единицу как частное , где , a ≠ 0.

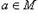
Теорема 2. Пересечение (в смысле пересечения множеств) любого множества надполей поля P опять является подполем поля P.

Соответствующая теорема верна и для колец, т. е. пересечение любого множества подколец кольца R есть подкольцо кольца R. Доказательство ее вполне аналогично данному здесь для полей.

Доказательство. Пусть <M_s> есть некоторое множество подполей, где индексы s образуют множество S и — пересечение всех подполей M_s данного множества; 0 и 1 входят в каждое подполе M_s и, значит, в D. Итак, D содержит не менее двух элементов. Если aиb — элементы D, то они входят в каждое M_s и по теореме 5 a + b, a — b, ab, а при b ≠ 0 и также входят в M_s, а значит, и в D. В силу теоремы 5 D — подполе поля P.

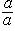
Поле, не имеющее подполей, отличных от него самого, называется простым.

Примерами простых полей могут служить поле рациональных чисел и поля вычетов по простому модулю p.

Любое подполе M поля P рациональных чисел содержит число 1, а значит, и все его кратные n · 1 = n, т. е. все целые числа, а значит, и все их частные, т. е. все рациональные числа. Итак, M = P, т. е. P — простое поле. Точно так же любое подполе M поля C_pвычетов по простому модулю p содержит класс (1), служащий единицей C_p, а значит, любой класс (r) как r-кратное класса (1). Итак, M= C_p, т. е. C_p — простое поле.

Можно доказать, что этими полями в некотором смысле исчерпываются все простые поля.

Теорема 3. Любое поле содержит простое подполе и притом только одно.

Доказательство. Поле P вообще содержит подполя (например, само P). Пусть D есть пересечение всех подполей поля P. По теореме 6 D является подполем P и по самому определению входит в любое подполе. Пусть M — подполе D, отличное от D.

Из определения подполя следует, очевидно, что M будет подполем и для P, и D не входит в M, что невозможно. Итак, D — простое подполе P. Если D’ — также простое подполе поля P, то пересечение будет опять подполем поля P, причем и . Но из определения подполя следует, что в таком случае D» будет подполем как для D, так и для D’, а так как D и D’ — простые подполя, то D = D» = D’, чем доказана единственность простого подполя.

Расширения полей

Расшире́ние по́ля K — поле E, содержащее данное поле K в качестве подполя. Исследование расширений является важной задачей теории полей, так как любой гомоморфизм полей является расширением.

Базовые определения

Если E — поле, его подполе — это его подмножество K, замкнутое относительно сложения и умножения, взятия обратного и противоположного элементов и содержащее единицу, на котором введены те же операции, что и в поле E. В этом случае E называется расширением поля K, заданное расширение обычно обозначают E\supset K (также используются обозначения E/K и K\subset E). Любой гомоморфизм полей инъективен, то есть является вложением. Из этого следует, что задание конкретного расширения E\supset K эквивалентно заданию гомоморфизма f:K\to E.

Если задано расширение E\supset K и подмножество S поля E, то наименьшее подполе E, содержащее K и S, обозначается K(S) и называется полем, порождённым множеством S над полем K. Расширения, порождённые одним элементом, называются простыми расширениями, а расширения, порождённые конечным множеством — конечно порождёнными расширениями.

Для любого расширения E\supset K E является векторным пространством над полем K. В этой ситуации элементы E можно понимать как «векторы», а элементы K — как «скаляры», умножение вектора на скаляр задаётся операцией умножения в поле E. Размерность этого векторного пространства называется степенью расширения и обозначается [E:K]. Расширение степени 1 называется тривиальным, расширения степени 2 и 3 — квадратичными и кубическими соответственно. Расширение конечной степени называют конечным, в противном случае — бесконечным.

Алгоритм решения систем линейных уравнений в кольцах вычетов

Алевтина Шахова 6 лет назад Просмотров:

1 Авдошин С.М., Савельева А.А. Алгоритм решения систем линейных уравнений в кольцах вычетов Разработан эффективный алгоритм решения систем линейных уравнений в кольцах вычетов [], эквивалентный по сложности известному алгоритму решения систем в полях Галуа ([2], [4]). Приведены результаты сравнительного анализа предложенного алгоритма и существующих аналогов ([3], [0], [8]) на основе асимптотической оценки их временной сложности. Показано, что разработанный метод является корректным и существенно снижает трудоемкость алгоритмов дискретного логарифмирования. Введение Объектом исследования данной работы являются методы решения систем линейных уравнений в кольцах вычетов. Такие системы возникают в алгоритмах факторизации и дискретного логарифмирования (см., например, метод Диксона, алгоритм Копперсмита-Одлыжко-Шреппеля «COS» и алгоритм решета числового поля в [3]). Частным случаем колец вычетов являются поля Галуа, т.е. кольца вычетов по модулю простых чисел. Методы решения систем в таких полях известны (см., например, метод Гаусса (последовательного исключения) в [2, с.89], [4, с.42]). Модификацией метода Гаусса является метод Жордана. Однако для решения систем линейных уравнений в кольцах вычетов эти методы, вообще говоря, неприменимы. Проиллюстрируем сказанное. Рассмотрим систему линейных уравнений: 26x+ 3y = 4 () 9x+ 34y = в поле Галуа Z 37 и в кольце вычетов Z 36. В соответствии с методом Жордана требуется с помощью элементарных преобразований над строками привести матрицу к единичной. Для получения единичного элемента на диагонали в поле действительных чисел используется деление на число a, равное ведущему элементу; аналогом этой операции в кольце вычетов является умножение на элемент, обратный к a. Обратный элемент по модулю можно найти как решение уравнения: ax (mod ) (2) Для его вычисления используется расширенный алгоритм Евклида (см. [7, с. 744], [0, с.227]). На рис. приведено описание этого алгоритма. Если a и — взаимно простые числа, т.е. НОД( a, ) = = ax + y, то 2 ; в противном случае коэффициент Безу x является решением уравнения ( ) уравнение ( ) 2 не имеет решения и элемент a необратим в кольце Z. Как показано в [7, с.743], время работы алгоритма Евклида при вычислении НОД ( ab, ), где a > b 0, составляет O(log b ). Тогда

2 сложность операции вычисления обратного элемента в кольце Z можно оценить как O(log ). Метод Жордана с учетом алгоритма Евклида имеет временную сложность O( n ( n m+ log ) ) для системы n уравнений с m неизвестными в Z. Евклид( ab, ). d x y a 0 n r s b 0 2. c d / n 3. d x y 0 d x y n r s c n r s 4. ЕСЛИ n > 0 5. ТО перейти к шагу 2; 6. ИНАЧЕ вернуть( d, x, y, r, s ) Рис. В результате вычислений, приведенных ниже, получаем решение системы в поле Галуа Z 37 : x = 6, y = 23. [] [] ( 26 = 0 ) 30 3 [2] [] [2] [] 30 3 [2] ( 23 = 29 ) 30 3 [] [2] [2] Однако в кольце вычетов по модулю = 36 система () не может быть решена ни с помощью метода Жордана, ни с помощью метода Гаусса, поскольку все коэффициенты при неизвестных являются делителями нуля ([9, с.75]) и, следовательно, не является обратимыми. Таким образом, получить единичный элемент на диагонали умножением на какой-либо элемент кольца невозможно. Тем не менее, конечность области определения позволяет убедиться в том, что решение данной системы в Z 36 существует ( x = 7, y = 22), и притом единственно. Для решения систем линейных уравнений в кольцах вычетов необходимы специальные методы. Обзор существующих методов Анализ методов решения систем линейных уравнений в кольцах вычетов, описанных в современной литературе, выявил ряд недостатков, которые затрудняют использование этих алгоритмов на практике. В монографии [3] задача сводится к решению систем линейных уравнений над полями Галуа. Пусть

3 где систем t q α = m = ( ) ax b(mod ), i=, n 3 i i =, тогда решение системы ( ) m = 3 сводится к решению семейства ( ) ax b(mod q α ), i=, n, =, t 4 i i где неизвестные значения x (mod q α ) для фиксированного представляются в виде α α x x + x q x q (mod q ), 5 0, α Здесь 0 xl q, l = 0, α. Редуцируя систему ( 4 ) к модулю q, получаем систему уравнений: над полем Галуа виде ( ) q m = 5 с известными i0 поделив на i 0 ax b(mod q), i=, n ( ) Z. Если мы найдем все x,, 0 = m, то, подставляя x в x в систему ( ) 4, редуцируя ее к модулю q, мы получим систему линейных уравнений над полем 2 q и затем относительно неизвестных x,, = m, и т.д. В конечном счете, найдя значение x (mod q α ) для всех, мы восстановим x (mod ) по китайской теореме об остатках (см. [0, с.420]). 2 2 В нашем примере = 36 = 2 3, т.е. для решения одной системы в кольце вычетов придется решить 4 системы над полями Галуа. Но основным недостатком метода является необходимость разложения на множители числа : вопрос о существовании алгоритма факторизации с полиномиальной сложностью является одной из открытых проблем современной теории чисел. Другой метод предполагает сведение системы линейных уравнений в кольце вычетов к системе линейных диофантовых уравнений. При помощи одного из известных алгоритмов (см. [3] или [0]) расширенная матрица системы ( A b ) приводится к ступенчатому виду ( A b ) и вычисляется правая матрица перехода R размером ( m+ ) ( m+ ), такая, что: ( A b) R = ( A b ). На основании матрицы R можно получить общее решение системы. Проиллюстрируем применение данного способа на примере. Система линейных диофантовых уравнений, соответствующая системе ( ) в Z 36, имеет вид: 26x+ 3y+ 36v = 4. 9x+ 34y + 36v2 = Ее общее решение в кольце целых чисел: Z q

4 x = t t (-2492) y = t0 (-324) + t 5688, t0, t Z v = t0 (-857) + t 5048 v2 = 0 + t0 0 + t Редуцируя результат к модулю 36, получаем: x = 7, y = 22. Однако при решении систем линейных уравнений в кольцах вычетов наблюдается экспоненциальный рост длины коэффициентов. Так, в нашем примере коэффициенты исходной матрицы ограничены числом 36, тогда как в 6 целых числах мы получили общее решение с коэффициентами

0. Заметим, что этот результат соответствует системе в кольце вычетов, состоящей всего лишь из двух уравнений с двумя неизвестными. Для того, чтобы избежать экспоненциального роста длины коэффициентов, разработаны специальные методы решения систем линейных алгебраических уравнений над кольцом целых чисел, такие как модификация метода Гаусса и построение нормальной диагональной формы Смита (см. [8, с. 8]). Несмотря на то, что эти алгоритмы являются полиномиальными, их сложность существенно превышает сложность алгоритма Гаусса при решении систем в полях Галуа. Так, для системы из n уравнений с n неизвестными, коэффициенты которой по абсолютной величине не превосходят α, временная сложность модифицированного алгоритма Гаусса при использовании самого быстрого алгоритма умножения составляет O( n 4 (log α + log n ) ). Трудоемкость построения нормальной диагональной формы Смита матрицы 2 O n m 2 logα. A, где a α, i, n,, m n m i = =, ограничена величиной ( ) Метод решения систем линейных уравнений в кольцах вычетов, предлагаемый в данной работе, лишен недостатков вышеописанных алгоритмов и показал свою эффективность при программной реализации. Описание метода В основе разработанного метода лежит преобразование строк матрицы с использованием коэффициентов Безу, которые позволяет вычислить расширенный алгоритм Евклида (см. рис.). В результате работы алгоритма получаем: НОД ( ab, ) = d= a x+ b y, 0 = n = a r+ b s. a = 26 = a, b= 9 = a : НОД (26, 9) = = 26 ( ) + 9 (3), 0= 26 (9) + 9 ( 26). При 2 Применяя к -й и 2-й строке расширенной матрицы системы () преобразования, соответствующие преобразованиям алгоритма Евклида над поступающими на его вход коэффициентами a = 26 и a 2 = 9, в результате мы получаем матрицу, строчно эквивалентную исходной (см. [5, с.27]):

5 [] [] [2] [] [2] 9 34 [2] [] 9 34 [] [2] [] [2] [2] [] [] [2] [] [2] [2] В полученной матрице: A(, ) x y A(, ) = A(2, ) r s A(2, ), где x, y, r, s удовлетворяют условию: НОД ( a, a2) = a x + a2 y, 0 = a r + a2 s (запись A(, ) используется для обозначения -й строки расширенной матрицы A). Коэффициенты Безу x =, y = 3, r = 9, s = 26 можно получить, оперируя лишь коэффициентами a и a 2. Тогда цепь преобразований ( 6 ) сводится к одному преобразованию следующего вида: [] [] =[] 35 + [2] [2] =[] 9 + [2] 0 [2] С учетом того, что коэффициент a 22 = 7 обратим в Z 36 : 7 3(mod36), преобразуем матрицу к единичной и получаем решение: [] [] =[] + [2] [2] =[2] 3 [2] В общем виде алгоритм решения систем линейных уравнений в кольцах вычетов, представляющий собой модификацию метода Жордана, описан на рис.2. Доказательство корректности Предложенный алгоритм является корректным, т.е. полученная в результате преобразований система равносильна исходной (иначе говоря, решения системы не теряются и новые решения не появляются). 3 в матричном виде: Запишем систему уравнений ( ) Ax = b ( 7) Тогда по теореме о равносильности систем линейных уравнений: Если U — обратимая ( n n) коммутативное кольцо с единицей), тогда система уравнений ( ) системе ( UA) x = Ub. (Доказательство см. в [5, с.58]). Следствие из этой теоремы: ( 6) -матрица над R (R — произвольное 7 равносильна Если матрицы ( A, b ) и ( C, δ ) строчно эквивалентны, то система уравнений ( 7 ) равносильна системе Cx = δ.

6 Поскольку преобразования матрицы в описанном модифицированном методе Жордана базируются на элементарных преобразованиях строк (элементарными преобразованиями строк матрицы с элементами из коммутативного кольца с единицей называют (см. [6, с.85]) умножение любой ее строки на обратимый элемент кольца; прибавление к любой ее строке другой строки, умноженной на произвольный элемент кольца; транспозицию строк), то полученная на выходе алгоритма матрица строчно эквивалентна исходной (см. Модиф _ Жордан( A ). n Число _ Строк( A) 2. i 3. ДЛЯ = i+, n ЦИКЛ 4. НОД ( aii, ai ) = aii x + ai y ВЫЧИСЛИТЬ x, y, r, s : 0 = aii r + ai s 5. Ai (, ) x y Ai (, ) A(, ) r s A(, ) 6. ЕСЛИ коэффициент a ii необратим в Z 7. ТО выйти из алгоритма <матрица вырождена>8. ИНАЧЕ <обнуляем все элементы i го столбца выше ведущего>9. A(, i ) A(, i ) a ii 0. A(, ) A(, ) A( i, ) ai, =, i. i i+ 2. ЕСЛИ i n 3. ТО перейти к шагу 2; 4. ИНАЧЕ вернуть( A) [5, с.27]). Тогда приведенному выше следствию соответствующие системы уравнений являются равносильными. Что и требовалось доказать. Оценка сложности Предложенный алгоритм обладает временной сложностью ( ( log )) Рис.2 O n nm+ для системы в кольце вычетов по модулю, в которой n — число уравнений системы, m — число неизвестных. Для получения этой формулы воспользуемся оценкой временной b сложности алгоритма Евклида T( a, b) = O + logϕ НОД ( a, b), где a > b 0, ϕ = ( + 5) 2 (доказательство этой оценки предлагается в [7, с.745], в качестве упражнения). На каждом -м шаге процедура, реализующая алгоритм Евклида, вызывается раз: первым параметром является текущее значение ведущего

7 элемента, в качестве второго на вход последовательно подаются ai ( i = +, n) и. Пусть di — значение ведущего элемента на i -й итерации цикла: d0 = a, d = НОД ( a, a+, ) = НОД ( d0, a+, ). d = НОД ( d, a ). d = НОД ( d, a ). +, n n n, Тогда число операций оценивается неравенством: n < di ai, >min, + log ( n ) + log НОД ( d, a ). i= i i, Помимо этого, на каждом -м шаге над элементами матрицы производится порядка 2( n )( m+ ) 2nm операций. Число шагов алгоритма для системы равно n. Получаем временную сложность алгоритма: n ( ) ( ). Tn (, ) = 2 nm+ ( n ) + log On ( nm+ log ) = Заключение В заключение приведем сравнительный анализ временной сложности предложенного алгоритма и алгоритмов, описанных в современной литературе, для системы n уравнений с m неизвестными в кольце вычетов Z ( t q α = = ). Алгоритм Модифицированный метод Жордана Метод сведения к полям Галуа* Метод сведения к диофантовым уравнениям (с построением матрицы Смита) Временная сложность ( ( + log )) O n nm t O n ( n m α + log ) + ln lnln e = 2 O n m 2 log р ( ) ln ln ln *Оценка временной сложности этого метода дана при условии использования для разложения на множители числа наиболее эффективного на сегодняшний день (см. [7, c.779]) алгоритма «квадратичного решета» () Померанца, имеющего временную сложность L ( ) + o ln ln ln, где L ( ) e =.

8 Список литературы. Авдошин С.М., Савельева А.А. Свидетельство об официальной регистрации программы для ЭВМ : «Программа решения систем линейных уравнений в кольцах вычетов». Зарегистрировано в Реестре программ для ЭВМ Ван дер Варден Б.Л. Алгебра. — М.: Наука, с. 3. Василенко О.Н. Теоретико-числовые алгоритмы в криптографии. М.: МЦНМО, с. 4. Гантмахер Ф.Р. Теория матриц. Гостехиздат, с. 5. Глухов М.М., Елизаров В.П., Нечаев А.А. Алгебра: Учебник. В 2-х т. Т. I — М.: Гелиос АРВ, с. 6. Джекобсон Н. Теория колец (Перевод с английского Н. Я. Виленкина). М.: Государственное издательство иностранной литературы, с. 7. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. М.: МЦНМО, с. 8. Кузнецов М.И., Бурланков Д.Е., Чирков А.Ю., Яковлев В.А. Компьютерная алгебра: Учебник. Нижегородский Государственный Университет им. Н.И. Лобачевского. htt:// с. 9. Курош А.Г. Теория групп (Издание третье, дополненное). М.: «НАУКА», Главная редакция физико-математической литературы, с. 0. Ноден П., Китте К. Алгебраическая алгоритмика. Пер. с франц. — М.: Мир, с.