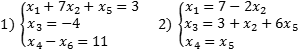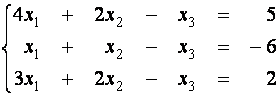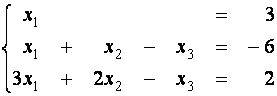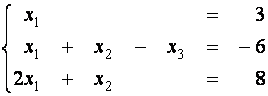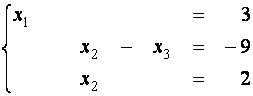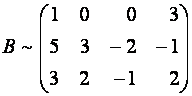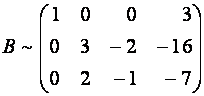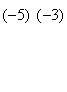Основные понятия системы линейных уравнений
Уравнение называется линейным, если оно содержит переменные (неизвестные) только в первой степени и не содержит произведений.
Линейное уравнение определяется, как уравнение вида:
a1, a2 … an — коэффициенты уравнения
b — свободный член (числа)
Если свободный член b=0, то уравнение называется однородным, а если иначе неоднороным.
Пусть система m линейных уравнений с n неизвестными имеет вид:
A — основная матрица коэффициентов системы;
A* — расширенная матрица;
X — матрица-столбец неизвестных;
B – матрица-столбец свободных членов.
Исходя из этого, систему можно представить в виде матричного уравнения, то есть в матричной форме:
A·X=B
Совместной называют систему линейных уравнений, если она имеет хотя бы одно решение. В ином случае несовместной, если не имеет решений.
Система линейных уравнений называется определенной, если она имеет единственное решение.
Система линейных уравнений называется неопределенной, если она имеет бесконечное множество решений.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.5 / 5. Количество оценок: 2
Системы линейных уравнений: основные понятия
— это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:
Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают, что число уравнений обязательно должно совпадать с числом переменных. В школьной алгебре так обычно и бывает, однако для высшей алгебры это, вообще говоря, неверно.
— это последовательность чисел ( k 1, k 2, . kn ), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x 1, x 2, . xn дает верное числовое равенство.
Соответственно, решить систему уравнений — значит найти множество всех ее решений или доказать, что это множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая:
- Система несовместна, т.е. множество всех решений пусто. Достаточно редкий случай, который легко обнаруживается независимо от того, каким методом решать систему.
- Система совместна и определена, т.е. имеет ровно одно решение. Классический вариант, хорошо известный еще со школьной скамьи.
- Система совместна и не определена, т.е. имеет бесконечно много решений. Это самый жесткий вариант. Недостаточно указать, что «система имеет бесконечное множество решений» — надо описать, как устроено это множество.
Переменная xi называется , если она входит только в одно уравнение системы, причем с коэффициентом 1. Другими словами, в остальных уравнениях коэффициент при переменной xi должен быть равен нулю.
Если в каждом уравнении выбрать по одной разрешенной переменной, получим набор разрешенных переменных для всей системы уравнений. Сама система, записанная в таком виде, тоже будет называться разрешенной. Вообще говоря, одну и ту же исходную систему можно свести к разным разрешенным, однако сейчас нас это не волнует. Вот примеры разрешенных систем:
Обе системы являются разрешенными относительно переменных x 1, x 3 и x 4. Впрочем, с тем же успехом можно утверждать, что вторая система — разрешенная относительно x 1, x 3 и x 5. Достаточно переписать самое последнее уравнение в виде x 5 = x 4.
Теперь рассмотрим более общий случай. Пусть всего у нас k переменных, из которых r являются разрешенными. Тогда возможны два случая:
- Число разрешенных переменных r равно общему числу переменных k : r = k . Получаем систему из k уравнений, в которых r = k разрешенных переменных. Такая система является совместной и определенной, т.к. x 1 = b 1, x 2 = b 2, . xk = bk ;
- Число разрешенных переменных r меньше общего числа переменных k : r k . Остальные ( k − r ) переменных называются свободными — они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.
Так, в приведенных выше системах переменные x 2, x 5, x 6 (для первой системы) и x 2, x 5 (для второй) являются свободными. Случай, когда есть свободные переменные, лучше сформулировать в виде теоремы:
Обратите внимание: это очень важный момент! В зависимости от того, как вы запишете итоговую систему, одна и та же переменная может быть как разрешенной, так и свободной. Большинство репетиторов по высшей математике рекомендуют выписывать переменные в лексикографическом порядке, т.е. по возрастанию индекса. Однако вы совершенно не обязаны следовать этому совету.
Теорема. Если в системе из n уравнений переменные x 1, x 2, . xr — разрешенные, а x r + 1, x r + 2, . x k — свободные, то:
- Если задать значения свободным переменным ( x r + 1 = t r + 1, x r + 2 = t r + 2, . xk = tk ), а затем найти значения x 1, x 2, . xr , получим одно из решений.
- Если в двух решениях значения свободных переменных совпадают, то значения разрешенных переменных тоже совпадают, т.е. решения равны.
В чем смысл этой теоремы? Чтобы получить все решения разрешенной системы уравнений, достаточно выделить свободные переменные. Затем, присваивая свободным переменным разные значения, будем получать готовые решения. Вот и все — таким образом можно получить все решения системы. Других решений не существует.
Вывод: разрешенная система уравнений всегда совместна. Если число уравнений в разрешенной системе равно числу переменных, система будет определенной, если меньше — неопределенной.
И все бы хорошо, но возникает вопрос: как из исходной системы уравнений получить разрешенную? Для этого существует метод Гаусса.
Каждое уравнение системы можно записать в более компактной форме
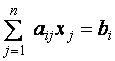
где 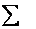
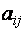
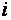
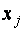
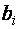
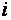
Упорядоченная совокупность 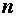
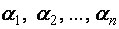
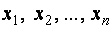
Другими словами: решением системы (1) является некоторый вектор 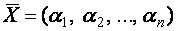
Система линейных уравнений, имеющая хотя бы одно решение, называется совместной, не имеющая ни одного решения, называется несовместной.
Совместная система линейных уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Две системы линейных уравнений с одними и теми же неизвестными называются равносильными, или эквивалентными, если каждое решение одной системы является решением другой системы, и наоборот (или если обе системы несовместны).
Элементарными преобразованиями системы (1) будем называть преобразования вида:
1. Перестановка любых двух уравнений;
2. Умножение какого-либо уравнения на число, отличное от нуля;
3. Прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на одно и то же число, отличное от нуля;
4. Отбрасывание уравнения, все коэффициенты которого и свободный член равны нулю.
Справедливо следующее утверждение.
Ø При элементарных преобразованиях система (1) переходит в равносильную ей систему.
Приведем пример решения системы линейных уравнений с помощью элементарных преобразований.
Пример 1 . Решите с помощью элементарных преобразований следующую систему линейных уравнений
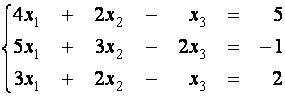
Будем использовать для обозначения эквивалентности систем уравнений знак Û .
(первое уравнение умножим на (-1) и прибавим ко второму)
(третье уравнение умножим на (-1) и прибавим к первому)
(второе уравнение умножим на (-1) и прибавим к третьему)
(первое уравнение умножим на (-1) и прибавим ко второму, а затем умножим его же на (-2) и прибавим к третьему)
(третье уравнение умножим на (-1) и прибавим ко второму)
(второе уравнение умножим на (-1) и после этого переставим с третьим)

Мы привели исходную систему к виду, разрешенному относительно неизвестных, откуда 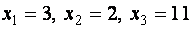
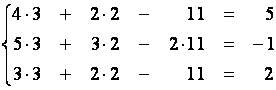

Получили три верные числовые равенства.
Итак, искомое решение 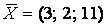
Анализируя процесс решения системы, сделаем несколько наблюдений.
1. В каждом уравнении преобразованной системы содержится ровно одна неизвестная (а остальные исключены), но четкого плана ее получения не видно.
2. Преобразованная система содержит 3 уравнения – столько же, сколько и исходная. Технически это понятно, так как использовались только три первые из элементарных преобразований, а четвертое применять не потребовалось.
3. В процессе преобразований уравнений системы фактически изменялись только ее коэффициенты и свободные члены.
Метод последовательного исключения неизвестных принадлежит великому немецкому математику Карлу Фридриху Гауссу (1777-1855) и, естественно, носит его имя.
Этот метод был усовершенствован известным французским математиком Камилем Мари Эдмоном Жорданом (1838-1922) и в новом виде стал называться методом Жордана-Гаусса .
Мы рассмотрим последовательно оба метода: метод Гаусса и метод Жордана-Гаусса .
В плане использования третьего наблюдения введем понятие матрицы.
Матрицей размера 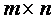
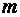
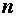
Числа, входящие в матрицу, принято называть ее элементами и обозначать 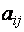
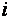
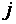
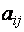
Сама матрица сокращенно обозначается символом 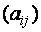
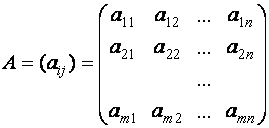
При этом 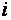
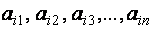
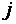
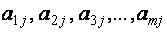
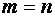
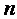
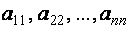
Матрица 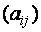
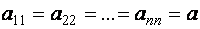
Скалярная матрица при 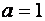
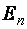
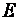
Треугольной будем называть квадратную матрицу, все элементы которой ниже (или выше) главной диагонали равны нулю.
Ступенчатой матрицей назовем матрицу, в которой каждая строка, кроме первой, начинается с нулей, причем их число возрастает с ростом номера строки, но последняя строка содержит по крайней мере один ненулевой элемент.
Примерами ступенчатой матрицы могут служить матрицы

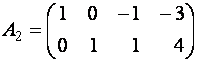
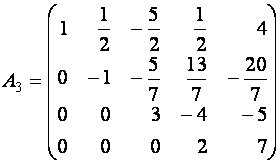

Заметим, что треугольная матрица является частным случаем ступенчатой. Примером треугольной матрицы служит матрица 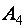
Теперь мы можем установить соответствие между системами линейных уравнений и матрицами.
Для каждой системы (1) 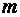
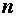
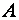
и матрицу 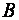
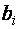
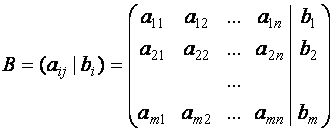
Таким образом, матрица 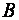
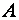
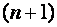
Матрицу 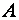
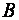
С другой стороны, имея матрицу 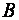
В полной аналогии с элементарными преобразованиями системы линейных уравнений введем элементарные преобразования строк матрицы:
1. Перестановка любых двух строк;
2. Умножение любой строки на число, отличное от нуля;
3. Прибавление к одной строке другой строки, умноженной на число, отличное от нуля;
4. Выбрасывание нулевой строки.
Если матрица 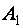
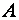
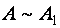
С помощью элементарных преобразований строк любую (ненулевую) матрицу можно привести к ступенчатому (в частности, треугольному) виду.
Покажем это на примере.
Пример 2 . Приведите к ступенчатому виду матрицу
Матрица 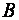
Можно было бы первую строку умножить на 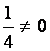
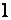
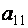
Поступим иначе: умножим третью строку на 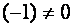
Теперь (для создания нулей в первом столбце) умножим первую строку новой матрицы на 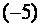
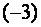
Умножим третью строку полученной матрицы на 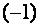
Умножим вторую строку на 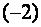
Матрица 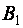
Цепочку преобразований матрицы 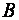
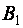



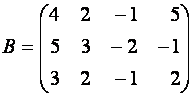

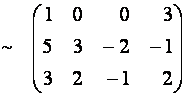


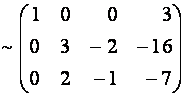



Замечание. Можно ввести понятие элементарных преобразований и для столбцов матрицы.
http://www.berdov.com/works/algebra/system_of_linear_equations/
http://lms2.sseu.ru/courses/eresmat/metod/met5/parmet5_1.htm