Система линейных уравнений плохо обусловлена если

7. Хорошо и плохо обусловленные системы

Существующие системы бывают плохо обусловленными и хорошо обусловленными.

Следует учитывать, как сильно могут повлиять погрешности округления на погрешность результата, какие свойства матрицы определяют ее «чувствительность» к погрешностям округления.

Существуют системы очень чувствительные к изменениям, проведенным в правой части уравнения системы. Рассмотрим два примера

Пример № 4 . Имеем систему

Решением системы является вектор x = (1,1).

Пример № 5. Имеем систему, отличную от системы примера № 4 изменением в правой части пятой значащей цифры:

Решением этой системы является вектор x = (0,2).

Из этих примеров можно сделать вывод, что изменение в правой части пятой значащей цифры повлекло изменение решения.

Заметим, что в обоих примерах определитель матрицы системы мал, и, по-видимому, система почти вырождена.

Таким образом, можно сделать вывод, что если Ах=b − совместная система с detA¹0 и матрица А почти вырождена, то малые изменения элементов системы могут привести к новой системе с det = 0, которая может оказаться несовместной, т. е. не иметь ни одного решения или иметь бесчисленное множество решений. Этот общеизвестный факт и рассмотренные примеры позволяют сделать вывод, что если матрица системы «почти вырождена», то ошибки округления могут привести к неверному результату. В таком случае нужно уметь заранее определить меру «близости» матрицы системы к множеству вырожденных матриц.

Мерой близости матрицы А к вырожденной является величина cond(A) − ­число обусловленности, которое вычисляется по формуле cond(A)=, где − норма матрицы А, а − норма обратной матрицы. (Порядок нахождения нормы матрицы приведен в [6]. Причем, чем больше величина cond(A), тем ближе матрица А к вырожденной.

Системы с большим числом обусловленности называют плохо обусловленными. Не существует численного метода, с помощью которого можно было бы устранить чувствительность плохо обусловленной системы к возмущениям элементов матрицы и правой части. Решение линейных систем с плохо обусловленными матрицами может оказаться некорректной задачей.

Проверить чувствительность решения системы к погрешностям можно и экспериментально. Для этого достаточно решить задачу несколько раз с несколькими близкими к bi правыми частями [3].

О ЧИСЛЕННОМ РЕШЕНИИ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С ПЛОХО ОБУСЛОВЛЕННЫМИ МАТРИЦАМИ

О ЧИСЛЕННОМ РЕШЕНИИ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С ПЛОХО ОБУСЛОВЛЕННЫМИ МАТРИЦАМИ
Научная статья
Рябов В.М. 1 , Бурова И.Г. 2, *, Кальницкая М.А. 3 , Малевич А.В. 4 , Лебедева А.В. 5 , Борзых А.Н. 6

1 ORCID: 0000-0002-1364-5428;
2 ORCID: 0000-0002-8743-1377;
3 ORCID: 0000-0001-5671-5070;
4 ORCID: 0000-0003-0753-4621;
5 ORCID: 0000-0001-9026-0292;
6 ORCID: 0000-0001-5489-911X;
1, 2, 3, 4, 5, 6 Санкт-Петербургский государственный университет, Санкт-Петербург, Россия

* Корреспондирующий автор (i.g.burova[at]spbu.ru)

Аннотация

Представлены результаты численного решения систем линейных алгебраических уравнений (СЛАУ) с симметричными и несимметричными плохо обусловленными матрицами методом регуляризации. Рассматриваются положительно определенные, а также осцилляционные матрицы. В статье показано, что для регуляризации вычислительного процесса по методу Тихонова достаточно заменить матрицу A_n системы матрицей где – единичная матрица, а a – некоторое положительное число (параметр регуляризации), которое стремится к нулю.

Ключевые слова: плохо обусловленные системы линейных алгебраических уравнений, матрицы Гильберта, параметр регуляризации.

ON NUMERICAL SOLUTION OF SYSTEMS OF LINEAR ALGEBRAIC EQUATIONS WITH ILL-CONDITIONED MATRICES
Research article
Ryabov V.M. 1 , Burova I.G. 2, *, Kalnitskaya M.A. 3 , Malevich A.V. 4 , Lebedeva A.V. 5 , Borzykh A.N. 6

1 ORCID: 0000-0002-1364-5428;
2 ORCID: 0000-0002-8743-1377;
3 ORCID: 0000-0001-5671-5070;
4 ORCID: 0000-0003-0753-4621;
5 ORCID: 0000-0001-9026-0292;
6 ORCID: 0000-0001-5489-911X;
1, 2, 3, 4, 5, 6 St. Petersburg State University, St. Petersburg, Russia

* Corresponding author (i.g.burova[at]spbu.ru)

Abstract

The results of the numerical solution of systems of linear algebraic equations (SLAE) with symmetric and asymmetrical ill-conditioned matrices by the regularization method are presented in the paper. Positive-definite and oscillatory matrices are considered. The article shows that in order to regularize the computational process according to the Tikhonov method, it is enough to replace the system matrix A_n with the matrix A_n + αE_n where E_n is the identity matrix, and α is some positive number (regularization parameter) that tends to zero.

Keywords: ill-conditioned systems of linear algebraic equations, Hilbert matrices, regularization parameter.

Введение
При решении различных задач возникает необходимость решать плохо обусловленные СЛАУ с положительно определенными симметричными матрицами. Такие системы линейных алгебраических уравнений возникают, например, когда функцию f (x) аппроксимируют алгебраическими многочленами в метрике пространства : если мы возьмем полином в виде и определим погрешность аппроксимации как то из условия минимизации придем к СЛАУ с матрицей Гильберта. Такие системы линейных алгебраических уравнений также возникают при решении обыкновенных дифференциальных уравнений методом Ритца, что приводит к матрицам Грама. Эти матрицы размерности n являются симметричными и положительно определенными, но при неограниченном увеличении n наименьшее собственное значение может стремиться к нулю, что приводит к неустойчивости решения.
Обычно для получения надежного решения используют методы регуляризации. Общей стратегией является использование стабилизатора Тихонова [1] или его модификаций [2], [3], [4], [5], [6], [7]. В этой статье рассматриваются особенности численного решения СЛАУ с положительно определенной симметричной матрицей с использованием регуляризации. В следующих разделах показано, что для регуляризации вычислительного процесса по методу Тихонова достаточно заменить матрицу системы A_n матрицей , где E_n – единичная матрица, а α – положительное число (параметр регуляризации), стремящееся к нулю. Таким образом, мы уменьшаем число обусловленности системы линейных алгебраических уравнений, что увеличивает устойчивость.
Постановка задачи
Пусть A – невырожденная вещественная квадратная матрица порядка n. В этом случае решение СЛАУ Az = f существует и единственно. Известны различные модификации метода Гаусса для решения СЛАУ, например, метод Гаусса с выбором ведущего элемента (в столбце или в матрице) и другие. Предположим, что число обусловленности матрицы A велико, т.е. матрица системы уравнений плохо обусловлена. Решение плохо обусловленных СЛАУ методом Гаусса не всегда дает удовлетворительное решение. Например, пусть
Число обусловленности матрицы A приближенно равно 10 7 . Решая эту систему методом Гаусса без перестановок (с помощью программы, написанной на C++ с вещественными числами типа double), получим z = (1.0? 1.555556, 0.666667) T , что существенно отличается от точного решения (1.0, 1.0, 1.0) T . Подобные примеры были рассмотрены в [6]. Эти примеры показывают, что в процессе решения необходимо избегать деления на малые по абсолютной величине элементы. Избежать эту ситуацию помогает использование модифицированного метода Гаусса, заключающегося в выборе ведущего элемента, являющегося наибольшим по абсолютному значению элементом в столбце (стратегия Уилкинсона) или по всей матрице (стратегия полного упорядочения Жордана) [2]. Применение метода Гаусса с выбором ведущего элемента по столбцам дает решение z = (1.0, 1.0., 1.0) T . Если система уравнений является плохо обусловленной, например, в случае СЛАУ с матрицей Гильберта порядка n с элементами , то практически невозможно получить приемлемое решение СЛАУ с помощью известных методов (прямыми методами, такими как метод Гаусса, метод квадратного корня, итерационными методами и др.).
В таблице 1 приведены числа обусловленности матриц Гильберта порядков от 3 до 20, полученные с помощью пакета Maple (Digits=50). В таблице 2 представлены решения СЛАУ Az = f c матрицами Гильберта H_n, полученные методом Гаусса (стратегия Уилкинсона). Здесь представлены решения, полученные при решении систем уравнений для n= 10, 12, 14, 20, вычисленные в C++ с числами типа double. Решения, представленные в таблице 2, далеки от истинных решений. В следующих разделах представлен метод регуляризации, с помощью которого получены решения исходной системы Az = f с матрицами Гильберта A = H_n при использовании нормы

Численное решение плохо обусловленной системы уравнений
Различные подходы к решению систем уравнений с плохо обусловленными матрицами известны (см. 2). В данной работе для получения приемлемого решения СЛАУ рассматривается применение модификации метода регуляризации. Известный стандартный метод регуляризации Тихонова позволяет найти нормальное решение системы Az = f. Этот метод основан на поиске элемента, на котором функционал достигает наименьшего значения для фиксированного положительного Для этого необходимо решить уравнение Эйлера – сопряженная матрица. Решение уравнения Эйлера зависит от числа обусловленности матрицы A * A . Это число может быть очень большим. Если матрица A симметрична и положительно определена, мы предлагаем найти нормальное решение другим способом. В данной работе предлагается найти нормальное решение путем решения системы уравнений, для которой число обусловленности значительно меньше.
Пусть матрица СЛАУ

является симметричной и положительно определенной (например, матрица Гильберта). В этом случае существует единственный положительно определенный корень из матрицы , т.е. положительно определенная матрица такая, что . Установим связь между собственными значениями и собственными векторами матриц и : пусть µ и собственное значение и собственный вектор матрицы :

Умножив (2) на B, получаем

Используя (2), перепишем (3) как . Это равенство означает, что собственные векторы матриц A и B одинаковы, а собственные значения матрицы A равны квадратам собственных значений матрицы B. Умножив (1) на , получаем

Запишем для (4) уравнение Эйлера для минимизации сглаживающего функционала : оно имеет вид

В случае симметричной матрицы матрица является самосопряженной, поэтому мы получаем уравнение

Формально в исходной системе осуществляется сдвиг, но фактически это метод регуляризации для уравнения (1).
В памяти компьютера числа обычно хранятся с некоторыми погрешностями. Будем считать, что матрица и вектор даны приближенно, т.е. вместо матрицы A и правой части известны такие, что δ. Говорить о сходимости можно лишь при неограниченном увеличении точности исходной информации, т.е. при δ→0. Однако практически мы не можем неограниченно уменьшать δ, из-за чего результаты могут быть далеки от желаемых решений. Решая задачу (6), получаем приближенное решение системы (1).
Замечание. Методы вычисления квадратного корня матрицы описаны в 9. Если матрица A симметрична, нам не нужно вычислять матрицу B. Применение регуляризации непосредственно к уравнению (1) просто увеличит число обусловленности результирующей системы, что невыгодно. В случае несимметричной положительно определенной матрицы уравнение Эйлера для системы (1) имеет вид (5). Сходимость метода регуляризации изложена в [1]. В отличие от стандартного подхода процедуры регуляризации представление (5) имеет меньшее число обусловленности, что очень важно. Но, в отличие от симметричных матриц, необходимо знать матрицу B в случае несимметричной матрицы. Последнее требование усложняет применение данного метода на практике.
Существуют классы несимметричных матриц, все собственные значения которых положительны. Покажем, как в этом случае можно осуществить процесс регуляризации в форме (5), а не в традиционной форме что, как уже упоминалось выше, существенно уменьшает число обусловленности решаемой системы. Рассматривается класс осцилляционных матриц (см. [12]), все собственные значения которых положительны и попарно различны, а соответствующие собственные векторы обладают особыми свойствами колебаний.
Пусть матрица A_n – осцилляционная, а V есть матрица собственных векторов – диагональная матрица собственных чисел A_n. Тогда Пусть _.Положим Понятно, что Таким образом, процесс регуляризации может быть осуществлен в форме (5). Обобщенная матрица Вандермонда, то есть матрица вида … -1 , 10 -2 ,…, 10 -12 для решения возмущенной СЛАУ где матрица исходной системы есть матрица Гильберта порядка n. Решение возмущенной системы получено методом Гаусса с выбором ведущего элемента по столбцам. Точное решение исходной невозмущенной системы H_nz = f есть n-мерный вектор из единиц: z = (1.0, 1.0, …, 1.0) T . Вычисляя решение возмущенной СЛАУ при различных значениях α, находим значение параметра, при котором погрешность решения имеет минимальное значение. Параметр α, соответствующий решению с наименьшей нормой, назовем оптимальным. Таким образом, для решения системы уравнений (1) необходимо решить несколько систем уравнений для различных α. В таблицах 3, 4 полужирным шрифтом выделено наименьшее значение нормы погрешности для заданного n, соответствующее оптимальному значению параметра возмущения α. В последней строке этих таблиц приведены нормы погрешностей решений, полученных без регуляризации. Погрешность решения вычислялась с помощью евклидовой нормы.

Точность арифметики с плавающей запятой можно охарактеризовать машинным ε, т.е. наименьшим положительным числом с плавающей запятой ε, для которого 1 + ε >1 (см. [6]). Мы можем вычислить машинное ε. Например, в 64-битном С++ переменные типа double дают

Теорема Тихонова утверждает, что теоретически, по мере уменьшения α, регуляризованное решение улучшается, но в практических расчетах для достаточно малых α (в пределах точности машины в C++) погрешности округления и число обусловленности матрицы имеют значительное влияние. Это можно увидеть, изучив результаты, представленные в начале таблиц 3, 4.
Заключение
В данной работе представлены результаты численного решения СЛАУ с положительно определенными симметричными (или несимметричными, но почти симметричными) плохо обусловленными матрицами модифицированным методом регуляризации. Показано, что решение СЛАУ с матрицами Гильберта с использованием метода регуляризации может быть существенно улучшено.

Список литературы / References

Устойчивость решения СЛАУ относительно исходных данных

(или обусловленность задач и вычислений)

Рассмотрим систему линейных алгебраических уравнений

,

Будем считать, что det A ¹ 0, .

Матрица А и вектор правой части во многих случаях задаются приближенно. Они получены либо в процессе эксперимента, либо в процессе каких-то промежуточных расчетов, содержащих соответственно погрешности эксперимента либо погрешности округления.

Естественно встает вопрос, как эти погрешности (возмущения) исходных данных влияют на точность решения. Чтобы на него ответить, надо познакомиться с особой характеристикой матриц, которую называют обусловленностью [3].

Таким образом, обусловленность характеризует устойчивость решения системы относительно исходных данных

Введем еще одно определение: задача решения СЛАУ является корректной, если решение существует, единственно (detA¹0) и непрерывно зависит от исходных данных (матриц А и В), т.е. малым изменениям исходных данных соответствуют малые изменения решения задачи.

Прежде всего, оговорим различие между плохо обусловленной задачей и плохо обусловленными вычислениями.

Если задача плохо обусловлена, то никакие усилия, потраченные на организацию изощренных вычислений, не могут дать правильный ответ, исключая случайность. С плохо обусловленными задачами можно столкнуться при расчетах стержневых систем методами строительной механики, например,

• при расчете рам методом перемещений, если два узла соединены очень жесткой частью конструкции;
• или при расчете конструкции методом сил, если выбрать основную систему так, что перемещение в устраняемой связи, соответствующее приложенной в ней паре нагрузок, равно или меньше перемещений в других устраненных связях от этой же нагрузки.

Все плохо обусловленные вычисления являются результатом применения численно неустойчивых алгоритмов. Например, метод исключения Гаусса без выбора главного элемента может обладать таким недостатком.

У плохо обусловленной матрицы обратная матрица является неустойчивой, т.е. элементы обратной матрицы значительно изменяются при малом изменении элементов исходной матрицы.

n Пример 3.7.Рассмотримплохо обусловленнуюсистему, записанную в матричном виде:

Если изменить правые части на 0,1 и принять их равными

то получим решение .

Если принять величину 1-го коэффициента в 1-ом уравнении равной 4,99 вместо 5, то получим решение .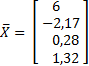

Существенно изменится при этом и обратная матрица.

Следует отметить, что чем больше порядок системы, тем сильнее сказывается влияние небольших возмущений коэффициентов системы на ее решение.

Обусловленность матрицы (системы) является качественной характеристикой, хотя мы будем стараться оценить ее количественно. Существует несколько способов оценки обусловленности.

Например, обусловленность матрицы (системы) можно оценить с помощью величины, называемой мерой обусловленности m(A):

где – норма матрицы А; – норма обратной матрицы.

Число m(A), часто обозначаемое cond A (от английского слова conditioned — «обусловленный»), служит также коэффициентом роста относительных погрешностей при неточном задании элементов матрицы А.

Чем больше m(A) ,тем сильнее сказываются возмущения в исходных данных на решении системы линейных уравнений. Если число m(A) велико, то система считается плохо обусловленной. Говорить о том, «что такое хорошо, а что такое плохо» в отрыве от контекста решаемой задачи почти бессмысленно, так как здесь могут играть роль размерность задачи, точность, с которой должно быть найдено ее решение, точность представления чисел в ЭВМ и т.п. Однако можно дать оценку снизу меры обусловленности. Число обусловленности m(A) не может быть меньше 1. Матрица, а соответственно и система, будет хорошо обусловленной, если m(A) стремится к единице.

n Пример 3.8. Оценим обусловленность матриц А и В:

A =

Решение:

Обратные матрицы равны:

=

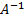
Вычислим меры обусловленности. Для этого найдем нормы матрицы А:

Мера обусловленности m(A) = 12´0,292=4,506 невелика и матрица А хорошо обусловлена.

Нормы матрицы В:

Мера обусловленности m(B) = 21´8421=176841 очень большая и матрица Вплохо обусловлена.

Примеры решения СЛАУ с использованием электронных таблиц MS Excel

Реализация метода Гаусса

Рассмотрим решение системы линейных алгебраических уравнений (пример 3.1) методом Гаусса, используя таблицы Excel.

Последовательность действий

Введем расширенную матрицу системы, как показано на рис.3.3, в ячейки А3:D5.

Рис.3.3. Реализация метода Гаусса в MS Excel

Прямой ход метода Гаусса.

1. Поделим элементы 1-ой строки на а_{11 .}Для этого в ячейку А7 введем формулу

и скопируем ее вправо до конца строки.

2. Умножим элементы 1-ой строки на (–а₂₁ ) и прибавим ко 2-й строке. Для этого введем формулу

и скопируем ее вправо до конца строки.

3. Умножим элементы 1-ой строки на (–а₃₁ ) и прибавим к 3-й строке. Для этого введем формулу

и скопируем ее вправо до конца строки.

Таким образом исключили неизвестное х₁ из 2-го и 3-го уравнений системы (смотри 1-й шаг рис.3.3).

Осталось исключить неизвестное х₂ из 3-го уравнения системы. Для этого реализуем описанный выше алгоритм для 2-й и 3-й строк (смотри 2-й шаг рис.3.3).

На этом прямой ход метода Гаусс закончен, матрица системы приведена к треугольному виду.

Обратный ход метода Гаусса.

Найдем последовательно неизвестные, начиная с последней строки. Для этого в ячейки G12:G14 запишем формулы:

G3=D12-C12*G4 (для вычисления x₂);

G2=D11-C11*G4-B11*G3 (для вычисления x₁).