VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Указатель — Разделы — Обозначения — Автор — О проекте
Вспомогательная страница к разделу ☞ МОДУЛЯРНАЯ АРИФМЕТИКА. Плохо обработанные заметки, и не уверен, что скоро вернусь к ним…
Найти двузначные натуральные числа, удовлетворяющие уравнению $ 17\, x+ 20\, y+45\, z =4111 $.
Решение. Выражаем $ x_<> $: $$ x=241-y-2\,z+\frac<14-3\,y-11\,z> <17>\ . $$ Полагаем $$ 17\, t_1 =14-3\,y-11\,z \quad \iff \quad 17\, t_1 + 3\,y+11\,z=14 \ . $$ Выражаем $ y_<> $: $$ y=4-3\,z-5\,t_1+\frac<2-2\,z-2\,t_1> <3>\ . $$ Полагаем $$ 3\, t_2=2-2\,z-2\,t_1 \quad \iff \quad 3\, t_2+2\,z+2\,t_1=2 \ . $$ Выражаем $ z_<> $: $$ z=1-t_1-t_2-\frac
Пример. Решить систему линейных уравнений в целых числах $$ \left\< \begin
Решение. Из второго уравнения выражаем $ x_ <2>$: $$x_2=-3+2\, x_1=t_1 \quad \Rightarrow \quad x_1=\frac<3+t_1>2=1+\frac
Ответ. $ x_1 = 1+t_2,\ x_2 =-1+2\,t_2,\ x_3=14-3\,t_2,\ x_4=4-t_2 $ при $ t_2 \in \mathbb Z $.
Решим теперь более сложный пример.
Пример. Решить систему линейных уравнений в целых числах $$ \left\< \begin
Решение. Имеем из первого уравнения: $$ x_1=\frac<11-7\,x_2-8\,x_3><5>=2-x_2-x_3+\frac<1-2\,x_2-3\,x_3> <5>\quad \Rightarrow \quad t_1=\frac<1-2\,x_2-3\,x_3> <5>\ . $$ Далее, $$ 2\,x_2+3\,x_3+5\,t_1=1 \quad \Rightarrow \quad x_2=\frac<1-3\,x_3-5\,t_1><2>=-x_3-2\,t_1+ \frac<1-x_3-t_1> <2>\quad \Rightarrow \quad t_2=\frac<1-x_3-t_1> <2>\ . $$ Получаем выражение для $ x_ <3>$: $$ x_3=1-t_1-2\,t_2 \ , $$ подставляем его в выражение для $ x_ <2>$: $$ x_2=-x_3-2\,t_1+t_2=-t_1=3\,t_2-1 \ . $$ Теперь $$ x_1=2-x_2-x_3+t_1=2+3\,t_1-t_2 \ . $$ Все три получившиеся формулы подставляем во второе уравнение системы: $$ 3\,t_1-23\,t_2=-8 \ . $$ Решаем это уравнение в той же технике, получаем: $$t_1=23\,u_2+5,\ t_2=3\, u_2+1 \ . $$ И возвращаемся к выражениям для $ x_1,x_2,x_3 $.
Ответ. $ x_1=16+66\, u_2,\ x_2=-3-14\, u_2,\ x_3=-6-29\, u_2 $ при $ u_2 \in \mathbb Z $.
Если бы мы решали предыдущую систему в рациональных или вещественных числах, то получили бы аналогичный вид решения: $$ x_1=x_<10>+66\, t,\ x_2=x_<20>-14\, t,\ x_3=x_<30>-29\, t \quad npu \quad t \in \mathbb R \ . $$ Можно проверить, что сомножители при $ t_<> $ — это величины миноров системы уравнений, т.е. $$ \left| \begin
Решение системы линейных уравнений в целых числах возможно еще симплекс-методом, но с этим я еще не разбирался. И следующий результат тоже выкладываю в надежде когда-нибудь разобраться…
Теорема [Минковский]. Рассмотрим систему вещественных линейных неравенств относительно неизвестных $ x_<1>,\dots,x_n $ $$ \left\< \begin
Решение систем линейных уравнений
Эта страничка поможет решить Системы Линейных Алгебраических Уравнений (СЛАУ) методом Гаусса, матричным методом или методом Крамера, исследовать их на совместность (теорема Кронекера-Капелли), определить количество решений, найти общее, частное и базисные решения.
Введите коэффициенты при неизвестных в поля. Если Ваше уравнение имеет меньшее количество неизвестных, то оставьте пустыми поля при переменных, не входящих в ваше уравнение. Можно использовать дроби ( 13/31 ).
Метод Гаусса онлайн
Данный онлайн калькулятор находит решение системы линейных уравнений (СЛУ) методом Гаусса. Дается подробное решение. Для вычисления выбирайте количество переменных и количество уравнений. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить.»
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Метод Гаусса
Метод Гаусса − это метод перехода от исходной системы линейных уравнений (при помощи эквивалентных преобразований) к системе, которая решается проще, чем исходная система.
Эквивалентными преобразованиями системы линейных уравнений являются:
- перемена местами двух уравнений в системе,
- умножение какого-либо уравнения в системе на ненулевое действительное число,
- прибавление к одному уравнению другого уравнения, умноженного на произвольное число.
Рассмотрим систему линейных уравнений:
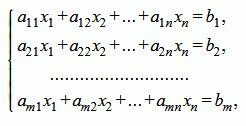 | (1) |
Запишем систему (1) в матричном виде:
| Ax=b | (2) |
  | (3) |
A-называется матрица коэффициентов системы, b − правая часть ограничений, x− вектор переменных, которую нужно найти. Пусть rang(A)=p.
Эквивалентные преобразования не меняют ранг матрицы коэффициентов и ранг расширеннной матрицы системы. Не меняется также множество решений системы при эквивалентных преобразованиях. Суть метода Гаусса заключается в приведении матрцы коэффициентов A к диагональному или ступенчатому.
Построим расшренную матрицу системы:
 | (4) |
Предположим a11≠0. Если это не так, то можно поменять местами эту строку со строкой с ненулевым элементом в столбце 1 (если нет таких строк, то переходим к следующему столбцу). Обнуляем все элементы столбца 1 ниже ведущего элемента a11. Для этого сложим строки 2,3, . m со строкой 1, умноженной на −a21/a11, −a31/a11, . −am1/a11, соответственно. Тогда (4) примет следующий вид:
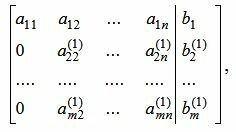 | (5) |
На следующем этапе обнуляем все элементы столбца 2, ниже элемента 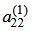
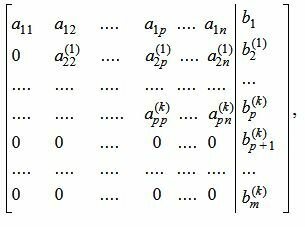 | (6) |
Обратим внимание на последние строки. Если 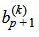

Пусть 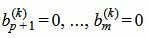
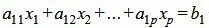 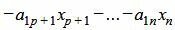 |
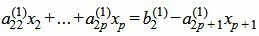  | (7) |
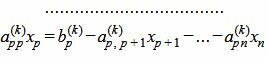 |
Так как rangA=rang(A|b), то множество решений (7) есть (n−p)− многообразие. Следовательно n−p неизвестных 
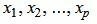
Примеры решения системы линейных уравнений методом Гаусса
Пример 1. Найти общее решение системы линейных уравнений методом Гаусса:
 |
Матричный вид записи: Ax=b, где
 |
Для решения системы, запишем расширенную матрицу:
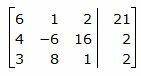 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строки 2,3 со строкой 1, умноженной на -2/3,-1/2 соответственно:
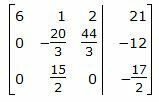 |
Исключим элементы 2-го столбца матрицы ниже элемента a2 2. Для этого сложим строку 3 со строкой 2, умноженной на 9/8:
 |
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
 |
Из вышеизложенной таблицы можно записать:
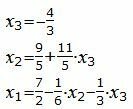 |
Подставив верхние выражения в нижние, получим решение.
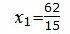 , ,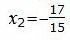 , ,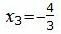 . . |
Пример 2. Найти общее решение системы линейных уравнений методом Гаусса:
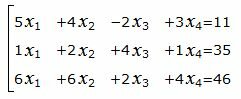 |
Матричный вид записи: Ax=b, где
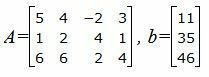 |
Для решения системы, построим расширенную матрицу:
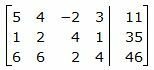 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/5,-6/5 соответственно:
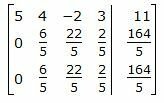 |
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 3 со строкой 2, умноженной на -1:
 |
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
 |
Выразим переменные x1, x2 относительно остальных переменных.
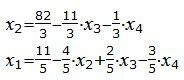 |
где x3, x4− произвольные действительные числа.
Подставив верхние выражения в нижние, получим решение.
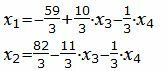 |
где x3, x4− произвольные действительные числа.
Векторный вариант решения:
Запишем вышеизложенное решение, представив свободные переменные в виде тождеств:
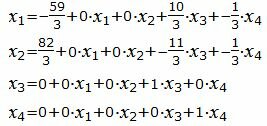 |
Тогда векторное решение можно представить так:
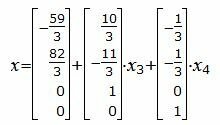 |
где x3, x4− произвольные действительные числа.
http://matrixcalc.org/slu.html
http://matworld.ru/calculator/gauss-method-online.php