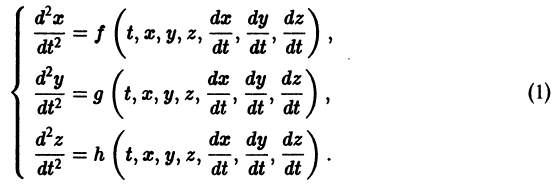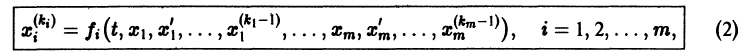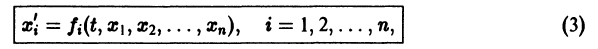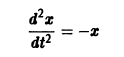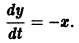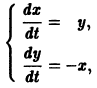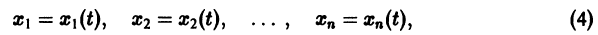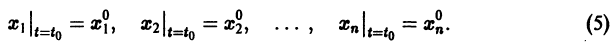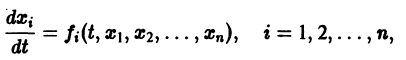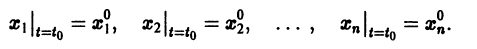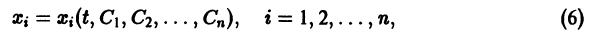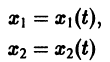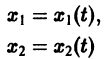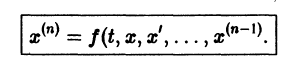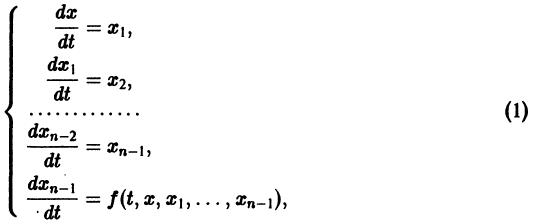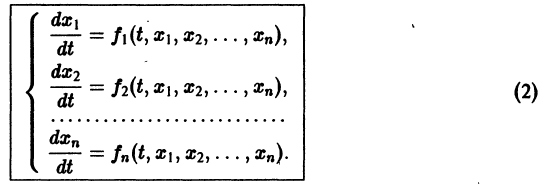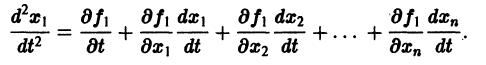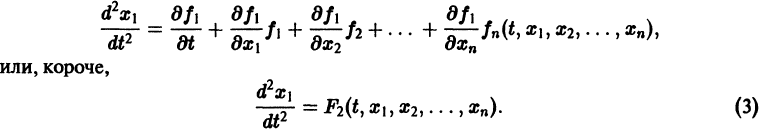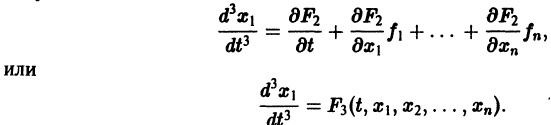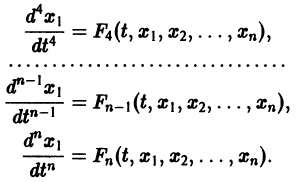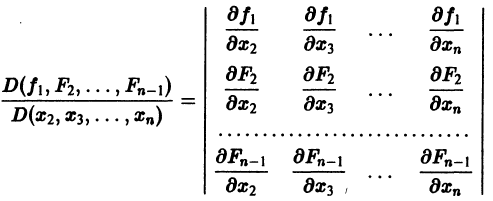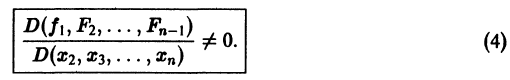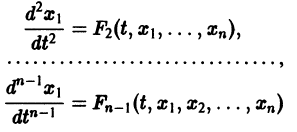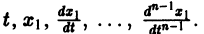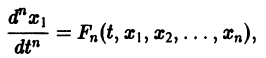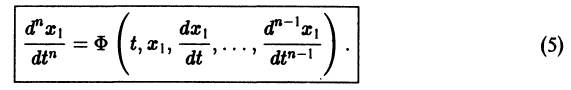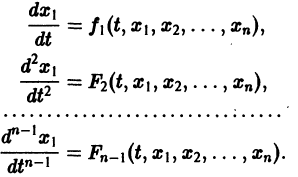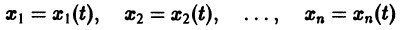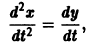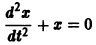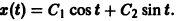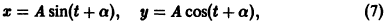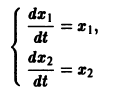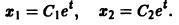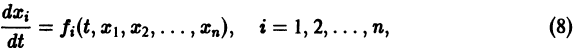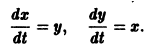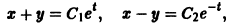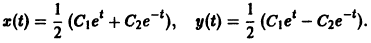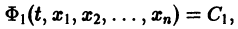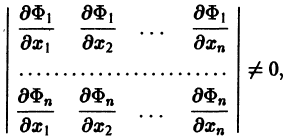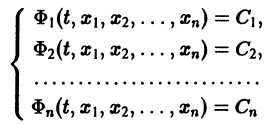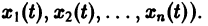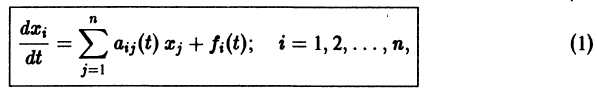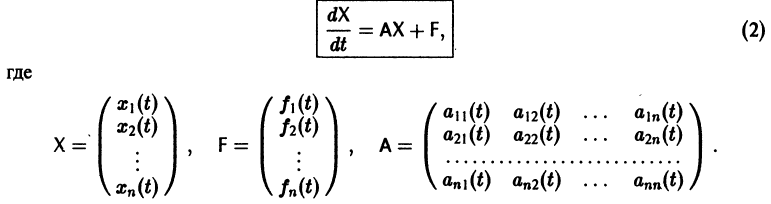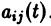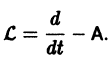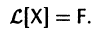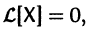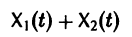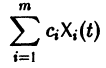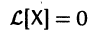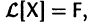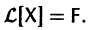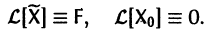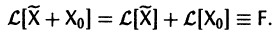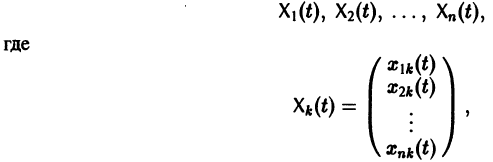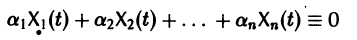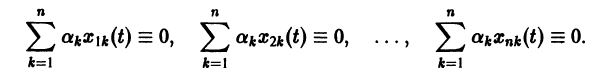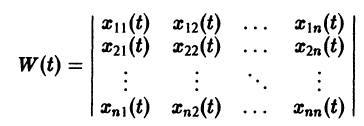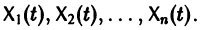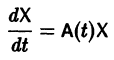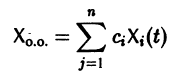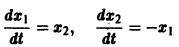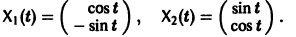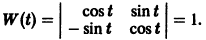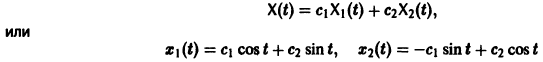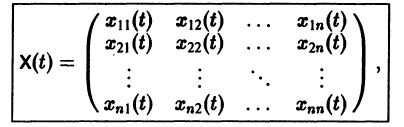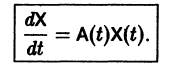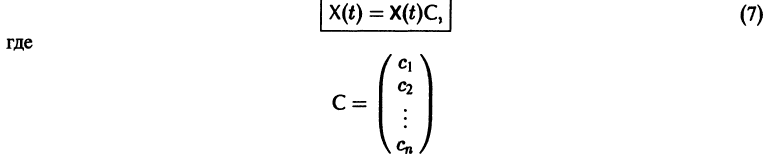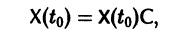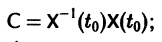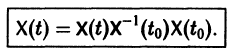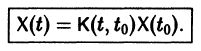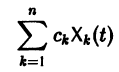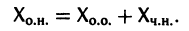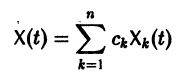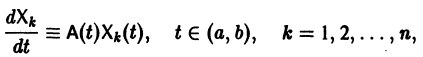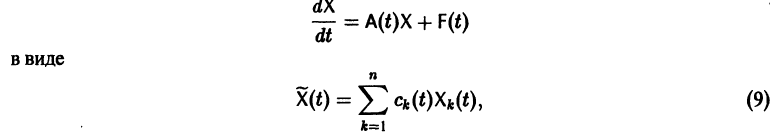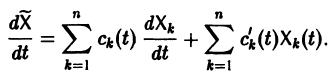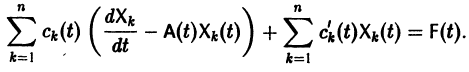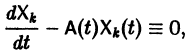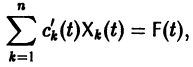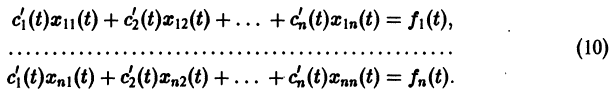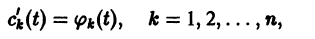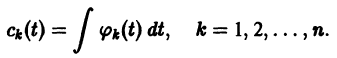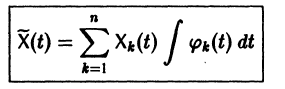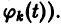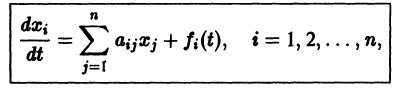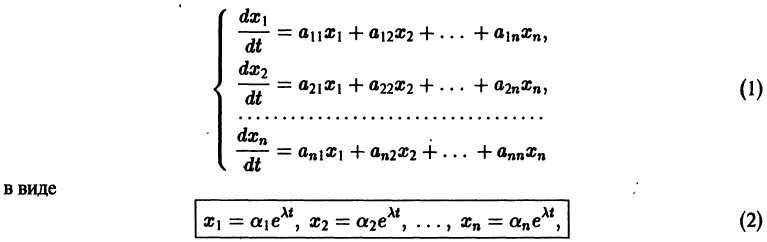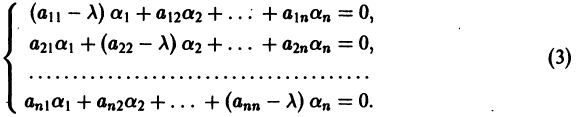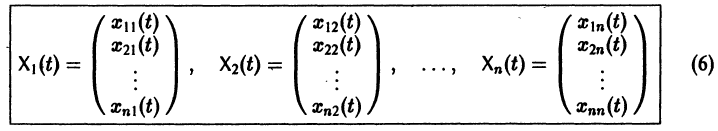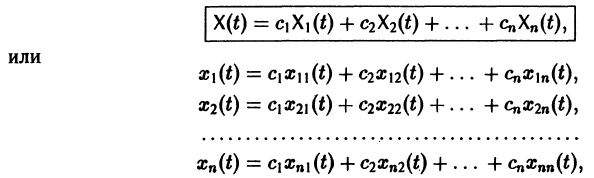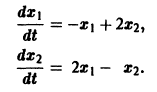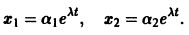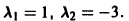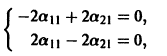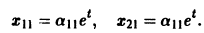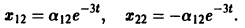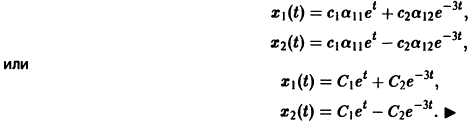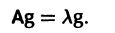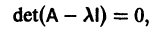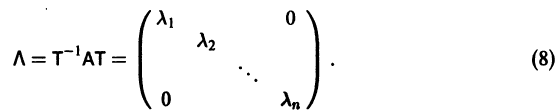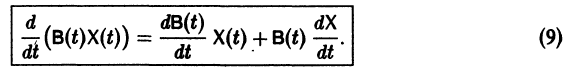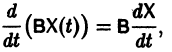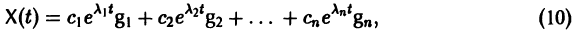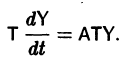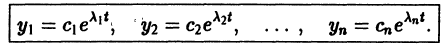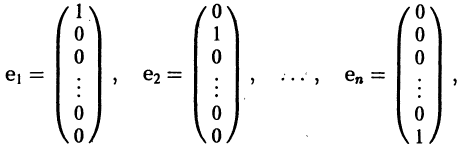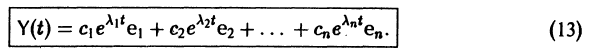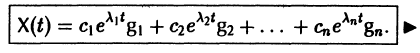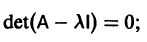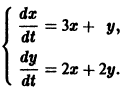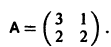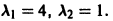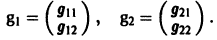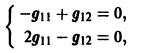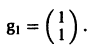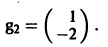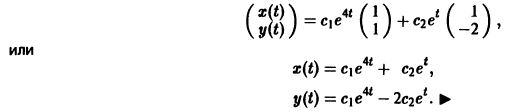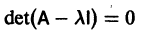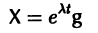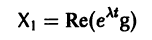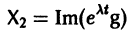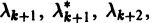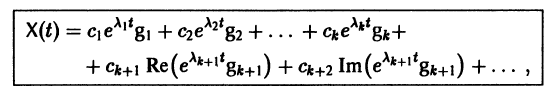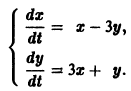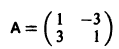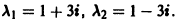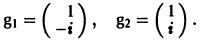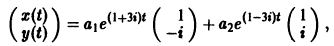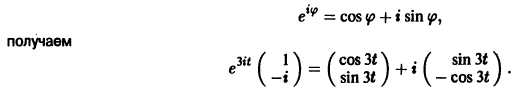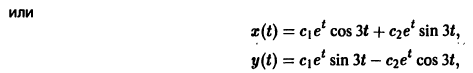Система линейных уравнений с вещественными коэффициентами

Системы дифференциальных уравнений с примерами решения и образцами выполнения

Также как и обыкновенные дифференциальные уравнения, системы дифференциальных уравнений применяются для описания многих процессов реальной действительности. В частности, к ним относятся различного рода физические и химические процессы, процессы нефте- и газодобычи, геологии, экономики и т.д. Действительно, если некоторые физические величины (перемещение тела, пластовое давление жидкости в фиксированной точке с тремя координатами, концентрация веществ, объемы продаж продуктов) оказываются меняющимися со временем под воздействием тех или иных факторов, то, как правило, закон их изменения по времени описывается именно системой дифференциальных уравнений, т.е. системой, связывающей исходные переменные как функции времени и производные этих функций. Независимой переменной в системе дифференциальных уравнений может выступать не только время, но и другие физические величины: координата, цена продукта и т.д.

Решение систем дифференциальных уравнений

К системе дифференциальных уравнений приводит уже простейшая задача динамики точки: даны силы, действующие на материальную точку; найти закон движения, т. е. найти функции 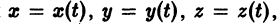выражающие зависимость координат движущейся точки от времени. Система, которая при этом получается, в общем случае имеет вид

Здесь x, у, z — координаты движущейся точки, t — время, f, g, h — известные функции своих аргументов.

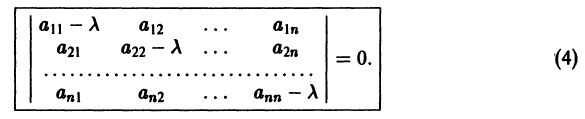
Система вида (1) называется канонической. Обращаясь к общему случаю системы т дифференциальных уравнений с т неизвестными функциями 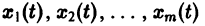аргумента t, назовем канонической систему вида

разрешенную относительно старших производных. Система уравнений первого порядка, разрешенных относительно производных от искомых функций,

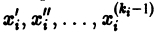
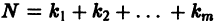
Если в (2) принять за новые вспомогательные функции, то общую каноническую систему (2) можно заменить эквивалентной ей нормальной системой, состоящей из уравнений. Поэтому достаточно рассматривать лишь нормальные системы.

Например, одно уравнение

является мастным случаем канонической системы. Положив 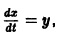в силу исходного уравнения будем иметь

В результате получаем нормальную систему уравнений

эквивалентную исходному уравнению.

Определение:

Решением нормальной системы (3) на интервале (а, Ь) изменения аргумента t называется всякая система n функций

дифференцируемых на интервале а

Теорема:

Существования и единственности решения задачи Коши. Пусть имеем нормальную систему дифференциальных уравнений

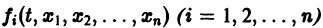
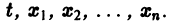
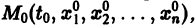
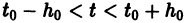
и пусть функции определены в некоторой (n + 1) — мерной области D изменения переменных Если существует окрестность точки в которой функции fi непрерывны по совокупности аргументов и имеют ограниченные частные производные по переменным то найдется интервал изменения t, на котором существует единственное решение нормальной системы (3), удовлетворяющее начальным условиям

Определение:

Система n функций

зависящих от t и n произвольных постоянных называется общим решением нормальной системы (3) в некоторой области существования и единственности решения задачи Коши, если

1) при любых допустимых значениях система функций (6) обращает уравнения (3) в тождества,

2) в области функции (6) решают любую задачу Коши.

Решения, получающиеся из общего при конкретных значениях постоянных называются частными решениями.

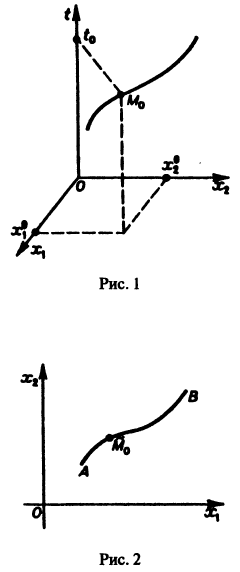
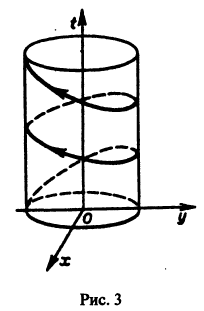
Обратимся для наглядности к нормальной системе двух уравнений,

Будем рассматривать систему значений t, x1, х2 как прямоугольные декартовы координаты точки трехмерного пространства, отнесенного к системе координат 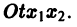Решение

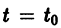
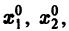
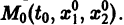
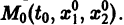
системы (7), принимающее при значения определяет в пространстве некоторую линию, проходящую через точку Эта линия называется интегральной кривой нормальной системы (7). Задача Коши для системы (7) получает следующую геометрическую формулировку: в пространстве переменных t, x1, х2 найти интегральную кривую, проходящую через данную точку (рис. 1). Теорема 1 устанавливает существование и единственность такой кривой.

Нормальной системе (7) и ее решению можно придать еще такое истолкование: будем независимую переменную t рассматривать как параметр, а решение

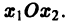
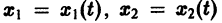
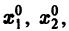
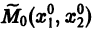
системы — как параметрические уравнения кривой на плоскости Эту плоскость переменных х1х2 называют фазовой плоскостью. В фазовой плоскости решение системы (7), принимающее при t = to начальные значения изображается кривой АВ, проходящей через точку (рис. 2). Эту кривую называют траекторией системы (фазовой траекторией). Траектория системы (7) есть проекция интегральной кривой на фазовую плоскость. По интегральной кривой фазовая траектория определяется однозначно, но не наоборот.

Методы интегрирования систем дифференциальных уравнений

Метод исключения

Один из методов интегрирования — метод исключения. Частным случаем канонической системы является одно уравнение n-го порядка, разрешенное относительно старшей производной

Введя новые функции 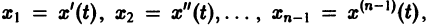заменим это уравнение следующей нормальной системой n уравнений:

т. е. одно уравнение n-го порядка эквивалентно нормальной системе (1)

Можно утверждать и обратное, что, вообще говоря, нормальная система п уравнений первого порядка эквивалентна одному уравнению порядка n. На этом и основан метод исключения для интегрирования систем дифференциальных уравнений.

Делается это так. Пусть имеем нормальную систему

Продифференцируем первое из уравнений (2) по t. Имеем

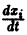
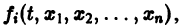
Заменяя в правой части производные их выражениями получим

Уравнение (3) снова дифференцируем по t. Принимая во внимание систему (2), получим

Продолжая этот процесс, найдем

Предположим, что определитель

(якобиан системы функций отличен от нуля при рассматриваемых значениях

Тогда система уравнений, составленная из первого уравнения системы (2) и уравнений

будет разрешима относительно неизвестных При этом выразятся через

Внося найденные выражения в уравнение

получим одно уравнение n-го порядка

Из самого способа его построения следует, что если 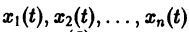есть решения системы (2), то функция х1(t) будет решением уравнения (5).

Обратно, пусть Х1(t) — решение уравнения (5). Дифференцируя это решение по t, вычислим 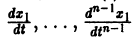и подставим найденные значения как известные функции

от t в систему уравнений

По предположению эту систему можно разрешить относительно т. е найти как функции от t.

Можно показать, что так построенная система функций

составляет решение системы дифференциальных уравнений (2). Пример:

Требуется проинтегрировать систему

Дифференцируя первое уравнение системы, имеем

откуда, используя второе уравнение, получаем

— линейное дифференциальное уравнение второго порядка с постоянными коэффициентами с одной неизвестной функцией. Его общее решение имеет вид

В силу первого уравнения системы находим функцию

Найденные функции x(t), y(t), как легко проверить, при любых значениях С1 и С2 удовлетворяют заданной системе.

Функции x(t), y(t) можно представить в виде

откуда видно, что интегральные кривые системы (6) — винтовые линии с шагом 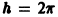и с общей осью х = у = 0, которая также является интегральной кривой (рис. 3).

Исключая в формулах (7) параметр t, получаем уравнение

так что фазовые траектории данной системы суть окружности с центром в начале координат — проекции винтовых линий на плоскость хОу.

При А = 0 фазовая траектория состоит из одной точки х = 0, у = 0, называемой точкой покоя системы.

Замечание:

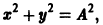
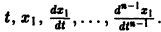
Может оказаться, что функции нельзя выразить через Тогда уравнения n-го порядка, эквивалентного исходной системе, мы не получим. Вот простой пример. Систему уравнений

нельзя заменить эквивалентным уравнением второго порядка относительно х1 или x2. Эта система составлена из пары уравнений 1-го порядка, каждое из которых интегрируется независимо, что дает

Метод интегрируемых комбинаций

Интегрирование нормальных систем дифференциальных уравнений

иногда осуществляется методом интегрируемых комбинаций.

Интегрируемой комбинацией называется дифференциальное уравнение, являющееся следствием уравнений (8), но уже легко интегрирующееся.

Пример:

Складывая почленно данные уравнения, находим одну интегрируемую комбинацию:

Вычитая почленно из первого уравнения системы второе, получаем вторую интегрируемую комбинацию:

Мы нашли два конечных уравнения

из которых легко определяется общее решение системы:

Одна интегрируемая комбинация дает возможность получить одно уравнение

связывающее независимую переменную t и неизвестные функции Такое конечное уравнение называется первым интегралом системы (8). Иначе: первым интегралом системы дифференциальных уравнений (8) называется дифференцируемая функция не равная тождественно постоянной, но сохраняющая постоянное значение на любой интегральной кривой этой системы.

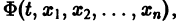
Если найдено п первых интегралов системы (8) и все они независимы, т. е. якобиан системы функций отличен от нуля:

то задача интефирования системы (8) решена (так как из системы

определяются все неизвестные функции

Системы линейных дифференциальных уравнений

Система дифференциальных уравнений называется линейной, если она линейна относительно неизвестных функций и их производных, входящих в уравнение. Система n линейных уравнений первого порядка, записанная в нормальной форме, имеет вид

или, в матричной форме,

Теорема:

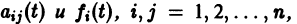
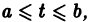
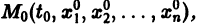
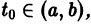
Если все функции непрерывны на отрезке то в достаточно малой окрестности каждой точки где выполнены условия теоремы существования и единственности решения задачи Коши, следовательно, через каждую такую точку проходит единственная интегральная кривая системы (1).

Действительно, в таком случае правые части системы (1) непрерывны по совокупности аргументов t, и их частные производные по ограничены, так как эти производные равны непрерывным на отрезке [а,b] коэффициентам

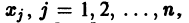
Введем линейный оператор

Тогда система (2) запишется в виде

Если матрица F — нулевая, т. е. 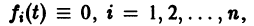на интервале (а,b), то система (2) называется линейной однородной и имеет вид

Приведем некоторые теоремы, устанавливающие свойства решений линейных систем.

Теорема:

Если X(t) является решением линейной однородной системы

то cX(t), где с — произвольная постоянная, является решением той же системы.

Теорема:

двух решений 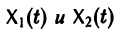однородной линейной системы уравнений является решением той же системы.

Следствие:

с произвольными постоянными коэффициентами сi решений 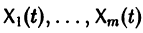линейной однородной системы дифференциальных уравнений

является решением той же системы.

Теорема:

Если 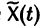есть решение линейной неоднородной системы

a Xo(t) — решение соответствующей однородной системы

будет решением неоднородной системы

Действительно, по условию,

Пользуясь свойством аддитивности оператора 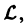получаем

Это означает, что сумма 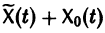есть решение неоднородной системы уравнений

Определение:

называются линейно зависимыми на интервале a

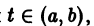
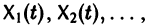
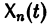
при причем по крайней мере одно из чисел аi, не равно нулю. Если тождество (5) справедливо только при то векторы называются линейно независимыми на (а, b).

Заметим, что одно векторное тождество (5) эквивалентно n тождествам:

называется определителем Вронского системы векторов

Определение:

Пусть имеем линейную однородную систему

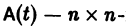
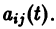
где матрица с элементами Система n решений

линейной однородной системы (6), линейно независимых на интервале а

с непрерывными на отрезке коэффициентами является линейная комбинация п линейно независимых на интервале а

() — произвольные постоянные числа).

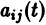
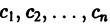
Пример:

имеет, как нетрудно проверить, решения

Эти решения линейно независимы, так как определитель Вронского отличен от нуля:

Общее решение системы имеет вид

(с1, с2 — произвольные постоянные).

Фундаментальная матрица

Квадратная матрица

столбцами которой являются линейно независимые решения 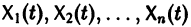системы (6), называется фундаментальной матрицей этой системы. Нетрудно проверить, что фундаментальная матрица удовлетворяет матричному уравнению

Если Х(t) — фундаментальная матрица системы (6), то общее решение системы можно представить в виде

— постоянная матрица-столбец с произвольными элементами. Полагая в (7) t = t0, имеем

Матрица 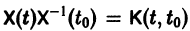называется матрицей Коши. С ее помощью решение системы (6) можно представить так:

Теорема:

О структуре общего решения линейной неоднородной системы дифференциальных уравнений. Общее решение в области 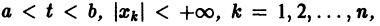линейной неоднородной системы дифференциальных уравнений

с непрерывными на отрезке коэффициентами aij(t) и правыми частями fi(t) равно сумме общего решения

соответствующей однородной системы и какого-нибудь частного решения 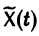неоднородной системы (2):

Метод вариации постоянных

Если известно общее решение линейной однородной системы (6), то частное решение неоднородной системы можно находить методом вариации постоянных (метод Лагранжа).

есть общее решение однородной системы (6), тогда

причем решения Xk(t) линейно независимы.

Будем искать частное решение неоднородной системы

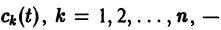
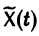
где неизвестные функции от t. Дифференцируя по t, имеем

Подставляя 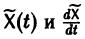в (2), получаем

то для определения 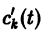получаем систему

или, в развернутом виде,

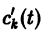
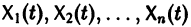
Система (10) есть линейная алгебраическая система относительно определителем которой является определитель Вронского W(t) фундаментальной системы решений . Этот определитель отличен от нуля всюду на интервале a

где 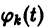— известные непрерывные функции. Интегрируя последние соотношения, находим

Подставляя эти значения 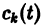в (9), находим частное решение системы (2)

(здесь под символом 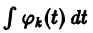понимается одна из первообразных для функции

Системы линейных дифференциальных уравнений с постоянными коэффициентами

Рассмотрим линейную систему дифференциальных уравнений

в которой все коэффициенты 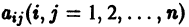— постоянные. Чаще всего такая система интегрируется сведением ее к одному уравнению более высокого порядка, причем это уравнение будет также линейным с постоянными коэффициентами. Другой эффективный метод интегрирования систем с постоянными коэффициентами — метод преобразования Лапласа.

Мы рассмотрим еще метод Эйлера интегрирования линейных однородных систем дифференциальных уравнений с постоянными коэффициентами. Он состоит в следующем.

Метод Эйлера

Будем искать решение системы

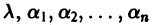
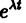
где — постоянные. Подставляя Xk в форме (2) в систему (1), сокращая на и перенося все члены в одну часть равенства, получаем систему

Для того, чтобы эта система (3) линейных однородных алгебраических уравнений с n неизвестными имела нетривиальное решение, необходимо и достаточно, чтобы ее определитель был равен нулю:

Уравнение (4) называется характеристическим. В его левой части стоит многочлен относительно степени n. Из этого уравнения определяются те значения , при которых система (3) имеет нетривиальные решения . Если все корни характеристического уравнения (4) различны, то, подставляя их по очереди в систему (3), находим соответствующие им нетривиальные решения этой системы n, следовательно, находим п решений исходной системы дифференциальных уравнений (1) в виде

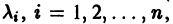
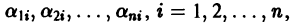
где второй индекс указывает номер решения, а первый — номер неизвестной функции. Построенные таким образом п частных решений линейной однородной системы (1)

образуют, как можно проверить, фундаментальную систему решений этой системы.

Следовательно, общее решение однородной системы дифференциальных уравнений (1) имеет вид

где произвольные постоянные.

Случай, когда характеристическое уравнение имеет кратные корни, мы рассматривать не будем.

Пример:

Ищем решение в виде

имеет корни

Система (3) для определения a1, а2 выглядит так:

Подставляя в (*) 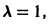получаем

откуда а21 = а11. Следовательно,

Полагая в 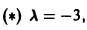находим a22 = — a12, поэтому

Общее решение данной системы:

Матричный метод

Изложим еще матричный метод интегрирования однородной системы (1). Запишем систему (1) в виде

матрица с постоянными действительными элементами

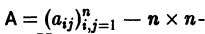
Напомним некоторые понятия из линейной алгебры. Вектор 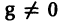называется собственным вектором матрицы А, если

Число называется собственным значением матрицы А, отвечающим собственному вектору g, и является корнем характеристического уравнения

где I — единичная матрица.

Будем предполагать, что все собственные значения матрицы А различны. В этом случае собственные векторы g1, g2, …gn линейно независимы и существует матрица Т, приводящая матрицу А к диагональному виду, т. е. такая, что

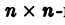
Столбцами матрицы Т являются координаты собственных векторов g1, g2 …, gn матрицы А.

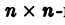
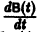
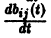
Введем еще следующие понятия. Пусть В(t) — матрица, элементы которой суть функции аргумента t, определенные на множестве . Матрица В(t) называется непрерывной на , если непрерывны на все ее элементы . Матрица В(t) называется дифференцируемой на , если дифференцируемы на все элементы этой матрицы. При этом производной матрицы называется матрица, элементами которой являются производные у соответствующих элементов матрицы В(t).

Пусть B(t) — n х n-матрица,

— вектор-столбец. Учитывая правила алгебры матриц, непосредственной проверкой убеждаемся в справедливости формулы

В частности, если В — постоянная матрица, то

так как 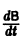есть нуль-матрица.

Теорема:

Если собственные значения матрицы А различны, то общее решение системы (7) имеет вид

где g1, g2,…, gn — собственные векторы-столбцы матрицы А, произвольные постоянные числа.

Введем новый неизвестный вектор-столбец Y(t) по формуле

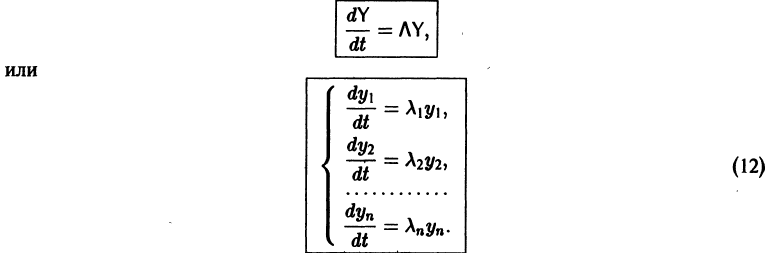
где Т — матрица, приводящая матрицу А к диагональному виду. Подставляя X(t) из (11) в (7), получим систему

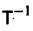
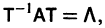
Умножая обе части последнего соотношения слева на и учитывая, что придем к системе

Мы получили систему из n независимых уравнений, которая без труда интегрируется:

Здесь 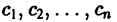— произвольные постоянные числа.

Вводя единичные n-мерные векторы-столбцы

решение Y(t) можно представить в виде

В силу (11) Х(t) = TY(t). Так как столбцы матрицы Т есть собственные векторы матрицы 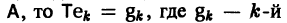собственный вектор матрицы А. Поэтому, подставляя (13) в (11), получим формулу (10):

Таким образом, если матрица А системы дифференциальных уравнений (7) имеет различные собственные значения, для получения общего решения этой системы:

1) находим собственные значения матрицы как корни алгебраического уравнения

2) находим все собственные векторы g1, g2,…, gn;

3) выписываем общее решение системы дифференциальных уравнений (7) по формуле (10).

Пример:

Матрица А системы имеет вид

1) Составляем характеристическое уравнение

Корни характеристического уравнения

2) Находим собственные векторы

Для = 4 получаем систему

откуда g11 = g12, так что

Аналогично для = 1 находим

3) Пользуясь формулой (10), получаем общее решение системы дифференциальных уравнений

Корни характеристического уравнения могут быть действительными и комплексными. Так как по предположению коэффициенты 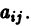системы (7) действительные, то характеристическое уравнение

будет иметь действительные коэффициенты. Поэтому наряду с комплексным корнем оно будет иметь и корень *, комплексно сопряженный с . Нетрудно показать, что если g — собственный вектор, отвечающий собственному значению , то * — тоже собственное значение, которому отвечает собственный вектор g*, комплексно сопряженный с g.

При комплексном решение

системы (7) также будет комплексным. Действительная часть

этого решения являются решениями системы (7). Собственному значению * будет отвечать пара действительных решений X1 и -Х2, т. е. та же пара, что и для собственного значения . Таким образом, паре , * комплексно сопряженных собственных значений отвечает пара действительных решений системы (7) дифференциальных уравнений.

Пусть — действительные собственные значения, — комплексные собственные значения. Тогда всякое действительное решение системы (7) имеет вид

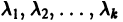
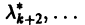
где сi — произвольные постоянные.

Пример:

1) Характеристическое уравнение системы

Его корни

2) Собственные векторы матриц

3) Решение системы

где а1, а2 — произвольные комплексные постоянные.

Найдем действительные решения системы. Пользуясь формулой Эйлера

Следовательно, всякое действительное решение системы имеет

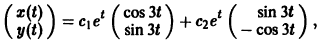
где с1, с2 — произвольные действительные числа.

Понятие о системах дифференциальных уравнений

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Система линейных уравнений с вещественными коэффициентами

Индивидуальные онлайн уроки: Отправьте запрос сейчас: irina@bodrenko.org
Математика (ЕГЭ, ОГЭ), Английский язык (разговорный, грамматика, TOEFL)
Решение задач: по математике, IT, экономике, психологии Итерационные методы решения линейных систем Учебные дисциплины на сайте Bodrenko.org
Портабельные Windows-приложения на сайте Bodrenko.com

Глава 6
ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ ЛИНЕЙНЫХ СИСТЕМ И ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ

В настоящей главе изучаются различные методы решения системы линейных уравнений с вещественными коэффициентами относительно неизвестных, также принимающих вещественные значения.
Все используемые на практике методы решения систем линейных уравнений можно разделить на две большие группы: точные методы и итерационные методы.
Под точным методом решения понимается метод, теоретически позволяющий получить точные значения неизвестных в результате проведения конечного числа арифметических операций. Примером точного метода может служить изложенный в гл. 3 метод, основанный на применении формул Крамера (практически метод, основанный на формулах Крамера, обычно не применяется, ибо он требует проведения очень большого числа арифметических операций и записей. Более удобным является точный метод, основанный на последовательном исключении неизвестных и называемый методом Гаусса (его изложение можно найти, например, в книге Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. — М.: Физматгиз, 1963, гл. 2)) .
Итерационные методы позволяют получить искомое решение лишь в виде предела последовательности векторов, построение которых производится с помощью единообразного процесса, называемого процессом итераций (последовательных приближений). Итерационные методы весьма удобны для использования современной вычислительной техники. Изложению наиболее употребительных итерационных методов решения линейных систем посвящен § 1 настоящей главы.
Итерационные методы находят широкое применение и при решении другой важной вычислительной задачи линейной алгебры — так называемой полной проблемы собственных значений (так называют проблему отыскания всех собственных значений и отвечающих им собственных векторов заданной матрицы (в отличие от этой проблемы, задачу отыскания некоторых (например, наибольших по модулю) собственных значений заданной матрицы называют частичной проблемой собственных значений)). В итерационных методах собственные значения вычисляются как пределы некоторых числовых последовательностей без предварительного определения коэффициентов характеристического многочлена.
В § 2 настоящей главы разбирается один из самых важных (наиболее употребительных на ЭВМ) итерационных методов решений полной проблемы собственных значений — так называемый метод вращений (или метод Якоби). Этот метод применим ко всякой симметричной (или к эрмитовой) матрице, легко реализуется на ЭВМ и всегда сходится. Он устойчив по отношению к ошибкам округления результатов промежуточных вычислений и обладает тем замечательным свойством, что наличие кратных и близких друг к другу собственных значений не только не замедляет его сходимости, а напротив, ускоряет ее. Метод вращений, предложенный Якоби и известный еще с середины прошлого века, долгое время не находил практического применения из-за большого объема вычислений, необходимых для его реализации. И лишь появление быстродействующих электронных вычислительных машин сделало его самым эффективным методом решения полной проблемы собственных значений симметричных и эрмитовых матриц.

§ 1. Итерационные методы решения линейных систем

I. Метод простой итерации (метод Якоби). Рассмотрим квадратную систему линейных уравнений с вещественными коэффициентами (3.10) (см. п. 1 §2 гл.З), которую запишем в матричном виде

понимая под А основную матрицу системы

а под X и F векторы-столбцы вида , первый из которых подлежит определению, а второй задан.
Предлагая однозначную разрешимость системы (6.1), заменим матричное уравнение (6.1) эквивалентным ему матричным уравнением X = X — τ АХ + τ F, в котором через τ обозначено вещественное число, обычно называемое стационарным параметром.
С помощью этого последнего уравнения составим итерационную последовательность векторов <Х_k >, определив ее рекуррентным соотношением

при произвольном выборе «нулевого» приближения X₀.
Метод простой итерации заключается в замене точного решения X системы (6.1) k -й итерацией Х _k с достаточно большим номером k . Оценим погрешность Z_k = Х _k — X метода простой итерации.
Из соотношений (6.3) и (6.1) сразу же вытекает следующее матричное уравнение для погрешности Z_k:

где Е — единичная матрица порядка n .
Введем в рассмотрение норму вектора в пространстве Е n и операторную норму квадратной матрицы порядка n . Как обычно, назовем нормой вектора X число ||Х||, равное корню квадратному из суммы квадратов координат этого вектора. Назовем операторной нормой произвольной матрицы А число || A || , равное либо точной верхней грани отношения ||АХ|| / ||Х|| на множестве всех ненулевых векторов X, либо (что то же самое) точной верхней грани норм ||АХ|| на множестве всех векторов X, имеющих норму, равную единице.
Итак, по определению

Напомним, что для любой симметричной матрицы А (матрица А называется симметричной, если А = А’) операторная норма этой матрицы равна наибольшему по модулю собственному значению этой матрицы (см. п. 4 § 5 гл. 5), т. е.

Из (6.5) вытекает следующее неравенство, справедливое для любой матрицы А и любого вектора X:

Из матричного уравнения для погрешности (6.4) и из неравенства (6.7) мы получим, что для любого номера k

Докажем теперь следующую простую, но важную теорему.
Теорема 6.1. Для того чтобы итерационная последовательность (6.3) при любом выборе нулевого приближения X₀ и при данном значении параметра τ сходилась к точному решению X системы (6.1), достаточно, чтобы было выполнено условие

ρ = || E — τ A || ρ .
В случае, если матрица А является симметричной, условие является и необходимым условием сходимости итерационной последовательности (6.3) при любом выборе нулевого приближения.
Доказательство. Для установления достаточности условия (6.9) заметим, что из неравенства (6.8) вытекает следующее соотношение:

Из (6.10) очевидно, что условие (6.9) обеспечивает сходимость последовательности погрешностей Z _k к нулю со скоростью геометрической прогрессии со знаменателем ρ .
В случае, если матрица А является симметричной, будет симметричной и матрица Е — τ А, а поэтому в силу (6.6) условие (6.9) можно переписать в эквивалентном виде

(здесь через < λ _s> обозначены собственные значения матрицы А).
Убедимся в том, что условие (6.11) является необходимым условием сходимости к нулю последовательности k> при любом выборе нулевого приближения Х₀. Предположим, что условие (6.11) не выполнено. Тогда существует собственное значение λ _s, удовлетворяющее неравенству |1 — τλ _s | ≥ 1. Обозначим через Х ( s) отвечающий этому собственному значению собственный вектор матрицы А и выберем нулевое приближение X₀ так, чтобы Z₀ совпало с X ( s) . Тогда, последовательно записывая соотношение (6.4) для номеров 1, 2. k , мы получим, что Z_k = (1 — τλ _s ) k Z₀. Из последнего соотношения в силу неравенства |1 — τλ _s | ≥ 1 вытекает, что || Z_k || не стремится к нулю при k → ∞ . Теорема 6.1 доказана.
Сразу же заметим, что для практических целей недостаточно установить только факт сходимости последовательности итераций. Центральной задачей численных методов является оценка скорости сходимости. Очень важно знать, как наилучшим способом распорядиться стационарным параметром г для того, чтобы получить наиболее быструю сходимость. Остановимся на этом вопросе подробнее.
Пусть задана ε -точность, с которой нам требуется получить точное решение системы (6.1). Требуется найти итерацию Х _k с таким номером k , для которого

Из (6.9) и (6.10) вытекает, что || Z_k || ≤ ρ k || Z₀ || и, стало быть, (6.12) выполняется при ρ k ≤ ε , т.е. при k ≥ ln(1 / ε ) / ln(1 / ρ ).
Отсюда видно, что для уменьшения числа итераций k , достаточных для достижения требуемой ε -точности, следует выбрать параметр τ так, чтобы получить минимум функции ρ = ρ ( τ ) = || E — τ A || .
Считая матрицу А симметричной и положительно определенной, мы приходим к следующей задаче оптимизации: найти минимум функции

Решение этой и несколько более общей задачи, предложенное А. А. Самарским, излагается в следующем пункте. Там будет доказано, что указанный минимум функции ρ = ρ ( τ ) достигается для значения τ = 2 / ( γ ₁ + γ ₂), где γ ₁ и γ ₂ — соответственно минимальное и максимальное собственные значения матрицы А, причем минимальное значение функции ρ ( τ ) равно

2. Общий неявный метод простой итерации. Снова обратимся к решению линейной системы (6.1), но на этот раз заменим итерационную последовательность (6.3) более общей итерационной последовательностью, определяемой соотношением

в котором В представляет собой некоторую «легко обратимую» квадратную матрицу n -го порядка, а τ — стационарный параметр. Такой метод составления итерационной последовательности и называется неявным методом простой итерации. Рассмотренный в предыдущем пункте явный метод простой итерации получается из неявного метода в частном случае В = Е, где Е — единичная матрица порядка n .
Для того чтобы сформулировать в удобной для приложений форме условие сходимости общего неявного метода простой итерации, напомним некоторые понятия, введенные в предыдущей главе.
Напомним, что матрица А называется положительно определенной, если (АХ, X) > 0 для любого ненулевого вектора X. В гл. 5 было доказано, что необходимым и достаточным условием положительной определенности симметричной матрицы А (или, что то же самое, самосопряженного линейного оператора А) является положительность всех собственных значений этой матрицы (этого оператора).
Если матрица А является положительно определенной, то мы договоримся писать неравенство А > 0. Далее договоримся писать неравенство В > А (или А 0 (т. е. если матрица В — А является положительно определенной).
Докажем следующую замечательную теорему (эта теорема является частным случаем доказанного известным советским математиком А. А. Самарским значительно более общего утверждения. (Самарский Л.Л. Введение в теорию разностных схем. — М.: Наука, 1971.)) .
Теорема 6.2 (теорема А. А. Самарского). Пусть матрица А является симметричной и выполнены условия А > 0, В > 0 (симметричность матрицы В, вообще говоря, не предполагается).
Тогда для того чтобы итерационная последовательность, определяемая соотношением

при любом выборе нулевого приближения X₀ сходилась к точному решению X системы АХ = F, достаточно, чтобы были выполнены условия

2В > τ А, τ А > 0. (6.14)

При дополнительном предположении о том, что матрица В является симметричной, условия (6.14) не только достаточны, но и необходимы для сходимости указанной итерационной последовательности при любом выборе нулевого приближения X₀.
Доказательство. 1) Достаточность. Прежде всего оценим погрешность Z_k = Х _k — X. Так как X удовлетвовлетворяет уравнению АХ = F, a X_k соотношению (6.13), то для Z_k получим соотношение

Установим для погрешности Z_k так называемое основное энергетическое соотношение.
Умножая (6.15) скалярно на вектор

Если воспользоваться обозначением С = 2В — τ А и соотношением

то равенство (6.16) можно переписать в виде

Далее заметим, что в силу симметрии матрицы А второе слагаемое в (6.17) равно (AZ_k+1, Z_k+1) — (AZ_k, Z_k). Это приводит нас к основному энергетическому соотношению:

Для доказательства достаточности условий (6.14) остается с помощью основного энергетического соотношения доказать сходимость к нулю последовательности < || Z_k || >.
Из основного энергетического соотношения и из положительной определенности матрицы С = 2В — τ А вытекает, что (AZ_k+1, Z_k+1) ≤ (AZ_k, Z_k), т.е. вытекает невозрастание последовательности <(AZ_k, Z_k)>. Из условия А > 0 вытекает, кроме того, что эта последовательность ограничена снизу нулем, а поэтому сходится.
Но тогда из основного энергетического соотношения следует, что

Напомним, что для положительно определенной матрицы С всегда найдется δ > 0 такое, что (СХ, X) ≥ δ ( Х, X) для любого вектора X или, что то же самое, || X || 2 ≤ (1/ δ ) (СХ, X). Последнее неравенство позволяет заключить, что из равенства нулю указанного выше предела (6.19) следует, что

Для завершения доказательства достаточности следует воспользоваться соотношением

из которого, в силу существования для положительно определенной матрицы А ограниченной обратной матрицы А -1 вытекает, что

Последнее равенство и соотношение (6.20) дают право заключить, что . Достаточность доказана.
Для доказательства необходимости условий (6.14) при дополнительном предположении о том, что матрица В симметрична, привлечем следующую лемму.
Лемма. Пусть С — некоторая симметричная матрица, а В — симметричная положительно определенная матрица. Тогда матрица С является положительно определенной в том и только в том случае, когда являются положительными все собственные значения задачи СХ = λ ВХ.
Для доказательства леммы заметим, что так как матрица В является симметричной и положительно определенной, то (в силу теоремы 5.24 из п.6 §5 гл.5) существует самосопряженный положительно определенный оператор В 1/2 такой, что для соответствующей ему матрицы В 1/2 справедливо равенство В 1/2 × В 1/2 = В. Так как матрица В 1/2 является положительно определенной и симметричной, то для нее существует ограниченная и симметричная обратная матрица, которую мы обозначим через В -1/2 .
Заметим далее, что с помощью замены X = В -1/2 У и умножения слева на матрицу В -1/2 задача на собственные значения СХ = λ ВХ переходит в эквивалентную задачу на собственные значения В -1/2 С В -1/2 Y , так что для доказательства леммы остается убедиться в том, что заведомо симметричная матрица В -1/2 С В -1/2 является положительно определенной тогда и только тогда, когда является положительно определенной матрица С. Это последнее сразу вытекает из того, что для любых ненулевых векторов X и Y , связанных соотношением Y = В -1/2 Х, справедливо равенство

(В -1/2 С В -1/2 Х, Х) = (С В -1/2 Х, В -1/2 Х) = (С Y, Y).

Лемма доказана.
Теперь мы можем перейти к доказательству необходимости условий (6.14) теоремы 6.2 при дополнительном предположении о том, что матрица В является симметричной.
2) Необходимость. Будем опираться на следующее утверждение из доказанной выше леммы: если матрица В является симметричной и положительно определенной, а матрица С является симметричной и не является положительно определенной, то задача на собственные значения СХ = λ ВХ имеет хотя бы одно неположительное собственное значение λ _s.
Предположим, что не выполнено первое из условий (6.14), т.е. не выполнено требование 2В — τ А > 0.
Полагая в проведенных выше рассуждениях С = 2В — τ А, мы получим, что задача на собственные значения (2В — τ А)Х = λ ВХ имеет хотя бы одно неположительное собственное значение λ _s. Обозначим через Х ( s) отвечающий λ _s собственный вектор и выберем нулевое приближение X₀ так, чтобы было выполнено условие Z₀ = Х ( s) .
Тогда, переписав уравнение для погрешности (6.15) в виде BZ_k+1 = — BZ_k + (2В — τ A)Z_k, мы получим, последовательно полагая k равным 0, 1.

Поскольку -1 + λ _s ≤ -1, то очевидно, что || Z_k || не стремится к нулю при k → ∞ .
Аналогично рассматривается случай невыполнения второго условия (6.14), т.е. условия τ А > 0. В этом случае в проведенных выше рассуждениях следует положить С = τ А. Мы получим при этом, что задача τ АХ = λ ВХ имеет хотя бы одно неположительное собственное значение λ _s с собственным вектором X (s) . Выбирая нулевое приближение X₀ так, чтобы было справедливо равенство Z₀ = Х ( s) и переписывая (6.15) в эквивалентном виде BZ_k+1 = BZ_k — τ AZ_k, мы получим, что

Так как λ ≤ 0, то очевидно, что || Z_k || не стремится к нулю при k → ∞ . Теорема 6.2 полностью доказана.
Перейдем теперь к оценке скорости сходимости общего неявного метода простой итерации. Следуя А. А. Самарскому ( Самарский А. А. Введение в теорию разностных схем. — М.: Наука, 1971; Самарский А.А., Гулин А.В. Устойчивость разностных схем. — М.: Наука, 1973), выясним вопрос о выборе такого значения параметра τ , которое обеспечивает наиболее быструю сходимость.
Предположим, что матрица В является симметричной и положительно определенной. С помощью такой матрицы естественно ввести так называемое энергетическое скалярное произведение двух произвольных векторов X и Y, положив его равным (ВХ, Y ) = (X, BY). Такое скалярное произведение будем обозначать символом (X, Y )_В.
С помощью матрицы В 1/2 это скалярное произведение можно записать в виде (X, Y )_В = (В 1/2 В 1/2 Х, Y ) = (В 1/2 Х, В 1/2 Y ). С помощью последнего равенства легко проверяется справедливость для введенного нами скалярного произведения четырех аксиом скалярного произведения (см. п. 1 § 1 гл.4).
Далее естественно ввести энергетическую норму вектора X, положив ее равной . Эту энергетическую норму мы обозначим символом ||Х||_В.
Две различные нормы одной и той же совокупности векторов ||X|| _I и ||Х|| _II называют эквивалентными, если существуют такие положительные постоянные γ ₁ и γ ₂, что справедливы неравенства

Заметим, что энергетическая норма вектора X и обычная его норма являются эквивалентными. В самом деле, справедливость неравенства γ ₁||X|| ≤ ||Х|| _B , т.е. неравенства γ 2 ₁(Х, X) ≤ (ВХ, X) вытекает из положительной определенности матрицы В, а справедливость неравенства ||Х|| _B ≤ γ ₂||X||, т.е. неравенства (ВХ, X) ≤ γ 2 ₂||X|| 2 вытекает из неравенства Коши-Буняковского и оценки (6.7) (достаточно положить γ 2 ₂ = ||В||).
Установленная эквивалентность обычной и энергетической норм позволяет утверждать, что последовательность ||Х _k || сходится к нулю тогда и только тогда, когда сходится к нулю последовательность ||Х _k ||_B.
Для дальнейших рассуждений энергетическая норма является более удобной, чем обычная норма.
Докажем следующую фундаментальную теорему.
Теорема 6.3 (теорема А. А. Самарского). Пусть матрицы А и В симметричны и положительно определены, Z_k обозначает погрешность общего неявного метода простой итерации. Тогда для того чтобы при ρ || Z_k || _B ≤ ρ k || Z₀ ||_B , достаточно, чтобы было выполнено условие

Замечание. А.А. Самарским доказано, что условие (6.21) не только достаточно, но и необходимо для справедливости неравенства || Z_k || _B ≤ ρ k || Z₀ ||_B , но мы на этом останавливаться не будем.
Доказательство теоремы 6.3. Для удобства разобьем доказательство на два шага.
1°. Сначала докажем, что если симметричные и положительно определенные матрицы А и В удовлетворяют условиям Самарского (6.14), то (ВZ_k+1, Z_k+1) ≤ (ВZ_k, Z_k).
Умножая равенство (6.15) скалярно на

В последнем равенстве заменим AZ_k на разность

Тогда, учитывая вытекающее из симметрии матрицы А равенство (A(Z_k+1 — Z_k), Z_k+1 + Z_k) = (Z_k+1 — Z_k, A(Z_k+1 + Z_k)), мы получим тождество

Учитывая, что (в силу условий Самарского (6.14)) операторы τ А и В-( τ /2)А являются положительно определенными, мы получим из последнего тождества следующее неравенство:

Это неравенство эквивалентно доказываемому неравенству

(в силу вытекающего из симметрии оператора В тождества (BZ_k+1, Z_k) = (Z_k+1, BZ_k)).
2°. Пусть теперь при ρ || Z_k || _B ≤ ρ k || Z₀ ||_B .
Положим Z_k = ρ k V_k . Тогда, очевидно,

Подставляя эти значения Z_k и Z_k+1 — Z_k в равенство (6.15) и производя сокращение на ρ k , получим для величин V_k следующее соотношение:

в котором = ρ В, .
В силу условий (6.21) операторы и Ã удовлетворяют условиям τ Ã > 0, 2 > τ Ã . Из этих условий и из того, что уравнение (6.22) для V_k совершенно идентично уравнению (6.15) для Z_k, в силу первого шага для V_k вытекает следующая оценка: .
Из этой оценки в свою очередь, учитывая, что = ρ В, получим неравенство (B V _k+1, V _k+1) ≤ (В V _k, B V _k).
Последовательное применение указанного неравенства для номеров k = 0, 1, . приводит нас к соотношению (BV_k, V_k) ≤ (BV₀, V₀), а умножение последнего соотношения на ρ 2 k приводит к окончательной оценке (мы учитываем, что Z_k = ρ k V_k, Z₀ = V₀) (BZ_k, Z_k) ≤ ρ 2k (BZ₀, Z₀).
Тем самым неравенство || Z_k || _B ≤ ρ k || Z₀ ||_B доказано. Доказательство теоремы 6.3 завершено.
В заключение применим теорему Самарского 6.3 для выяснения вопроса о выборе такого значения параметра τ , при котором скорость сходимости является максимальной. Из доказанной в теореме 6.3 оценки || Z_k || _B ≤ ρ k || Z₀ ||_B вытекает, что эта задача сводится к нахождению такого значения τ , при котором достигается минимальное значение функции ρ = ρ ( τ ).
Так как обе матрицы А и В симметричны и положительно определены, то существуют положительные постоянные γ ₁ и γ ₂ такие, что справедливы неравенства γ ₁B ≤ А ≤ γ ₂В. Будем считать, что постоянные γ ₁ и γ ₂ в этих неравенствах нам заданы (постоянные γ ₁ и γ ₂ естественно назвать константами эквивалентности матриц А и В. Для коммутирующих матриц А и В постоянные γ ₁ и γ ₂ соответственно равны наименьшему и наибольшему собственным значениям задачи АХ = λ ВХ). Сопоставляя только что написанные неравенства с условиями (6.21), мы получим, что минимальное значение ρ достигается при условии (1 — ρ ) / τ = γ ₁, (1 + ρ ) / τ = γ ₂, откуда получаем оптимальное значение τ = 2 / ( γ ₁ + γ ₂) и минимальное значение ρ , равное ( γ ₂ — γ ₁) / ( γ ₂ + γ ₁).
Частным случаем проведенного нами рассмотрения является явный метод простой итерации, изученный в п. 1. Для этого метода справедливы все полученные нами результаты.
В следующих трех пунктах с помощью общего неявного метода простой итерации и теоремы Самарского 6.2 мы рассмотрим несколько наиболее употребительных итерационных методов и установим условия их сходимости.
3. Модифицированный метод простой итерации. Этот метод получается из общего неявного метода простой итерации в том случае, когда стационарный параметр τ равен единице, а матрица В представляет собой диагональную матрицу D, состоящую из элементов матрицы А, лежащих на главной диагонали, т.е. В = D, где

При этом, конечно, предполагается, что матрица А является симметричной и что все ее диагональные элементы а₁₁, а₂₂, . а _nn являются положительными (последнее требование необходимо и достаточно для положительной определенности диагональной матрицы В = D).
Из теоремы 6.2 сразу же вытекает, что для сходимости модифицированного метода простой итерации при любом выборе нулевого приближения достаточно, чтобы были выполнены два условия: 2D > А, А > 0.
Теорема 6.1 позволяет выразить достаточное условие сходимости модифицированного метода простой итерации и в другой форме (мы учитываем, что в рассматриваемом случае вместо матрицы А следует взять матрицу Ã , определяемую формулой А = В -1 А и положить В = D, τ = 1) :

(под нормой матрицы, как и выше, понимается операторная норма).
Так как || Е — D -1 А || = || D -1 (D — А) || = || D -1 (A — D) || , то достаточное условие сходимости (6.24) можно переписать в эквивалентном виде

|| D -1 (A — D) || n будет справедливо неравенство (в этом неравенстве под нормой вектора понимается так называемая сферическая норма )

Из (6.26) и (6.5) сразу же вытекает, что операторная и сферическая нормы матрицы связаны соотношением ||А|| ≤ ||А||_сф.
Таким образом, в силу (6.25) достаточное условие сходимости модифицированного метода простой итерации выражается неравенством || D -1 (A — D) ||_{c ф} ‘ = U.
Метод Зейделя получается из общего неявного метода простой итерации в том частном случае, когда стационарный параметр τ равен единице, а матрица В равна сумме D + L. Таким образом, последовательные итерации в методе Зейделя определяются соотношением

Докажем, что метод Зейделя сходится для любой симметричной и положительно определенной матрицы А.
В силу теоремы 6.2 достаточно доказать, что для любой такой матрицы А выполнено условие

Для доказательства (6.27) заметим, что для любого вектора X

Таким образом, для доказательства неравенства (6.27) достаточно убедиться в положительной определенности матрицы D, но она сразу вытекает из того, что у положительно определенной и симметричной матрицы А все элементы, лежащие на главной диагонали, являются положительными (достаточно заметить, что если у вектора X k-я координата равна единице, а все остальные нулю, то (АХ, X) = а _kk > 0). Сходимость метода Зейделя доказана.
5. Метод верхней релаксации. Этот метод получается из общего неявного метода простой итерации в том частном случае, когда τ = ω , В = D + ω L, а параметр ω выбран так, чтобы являлось наименьшим наибольшее по модулю собственное значение матрицы Е — ω (D + ω L) -1 А, осуществляющей переход от k -й итерации к ( k + 1)-й.
Докажем, что если матрица А является симметричной и положительно определенной, то для сходимости метода верхней релаксации достаточно, чтобы было выполнено условие 0 ω ω > 0, 2(D + ω L) > ω A.
Второе из этих условий для любого вектора X приводит к неравенству

Последнее неравенство эквивалентно каждому из неравенств в следующей цепочке:

Из последнего неравенства и из положительной определенности D заключаем, что (6.28) справедливо при 2 — ω > 0, т. е. при ω ω Ã Х = , в котором = A’F, Ã = А ‘ А, так что матрица Ã является симметричной и (как легко убедиться) положительно определенной.
7. Итерационный метод П. Л. Чебышева (Пафнутий Львович Чебышев (1821-1894) — великий русский математик и механик) . Всюду выше при рассмотрении общего неявного метода простой итерации мы предполагали, что итерационный параметр τ принимает одно и то же постоянное значение. Естественно возникает идея рассмотреть более общий случай, когда в указанном методе значения итерационного параметра зависят от номера k итерации. В таком случае последовательность итераций будет определяться не соотношением (6.13)

а более общим соотношением

При этом, как и выше, В — некоторая легко обратимая квадратная матрица порядка n . При таком выборе итерационной последовательности для погрешности Z_k = Х_k — X итерационной схемы получится соотношение

Предположим, что обе матрицы А и В симметричны и положительно определенны. Тогда, как уже отмечалось выше, найдутся положительные постоянные γ ₁ и γ ₂ такие, что γ ₁B ≤ А ≤ γ ₂В. Будем считать, что эти постоянные γ ₁ и γ ₂ нам заданы и еще раз напомним, что эти постоянные равны соответственно наименьшему и наибольшему собственным значениям задачи АХ = λ ВХ. Оценим энергетическую норму погрешности ||Z_k||_В.
Напомним еще раз, что для симметричной и положительно определенной матрицы В существует симметричная и положительно определенная матрица В 1/2 такая, что В 1/2 • В 1/2 = В. Как и выше, договоримся обозначать символом В -1/2 матрицу, обратную к матрице В 1/2 .
Для оценки нормы погрешности Zk сделаем замену, положив Z_k = В -1/2 V_k. При такой замене соотношение для погрешности Z_k переходит в следующее соотношение для V_k:

где через С обозначена матрица вида С = В -1/2 АВ -1/2 . Убедимся в том, что квадрат обычной нормы вектора V_k равен квадрату энергетической нормы вектора Z_k. В самом деле,

Таким образом, для оценки энергетической нормы Z_k достаточно оценить обычную норму V_k.
Оценим норму || V_k ||. Прежде всего заметим, что из неравенств γ ₁(ВХ, X) ≤ (АХ, X) ≤ γ ₂(ВХ, X) с помощью замены X = В -1/2 Y получаются неравенства γ ₁( Y , Y) ≤ (CY, Y ) ≤ γ ₂( Y , Y ).
Последние неравенства эквивалентны тому, что γ ₁Е ≤ C ≤ γ ₂ E . Поскольку, кроме того, матрица С = В -1/2 АВ -1/2 симметрична, то все собственные значения этой матрицы вещественны и расположены на отрезке [ γ ₁, γ ₂]- Последовательно записывая соотношение V_k+l = (Е — τ _k+1С)V_k для номеров k = 0, 1. мы придем к следующему равенству:

из которого сразу же вытекает, что

Но тогда из равенства | |V_k || = ||Z_k||_В вытекает, что ||Z_k||_В ≤ q_k ||Z₀||_В, где . Следовательно, итерационный процесс сходится при условии, что последовательность < q_k > стремится к нулю, причем тем быстрее, чем меньше величины q_k .
Поскольку каждое значение q_k является функцией параметров τ₁ , τ ₂. τ _k , возникает задача построения оптимального набора итерационных параметров из условия минимума q_k для фиксированного k . Перейдем к решению этой задачи.
Предположим, что все собственные значения λ _s матрицы С лежат на заданном сегменте [ γ ₁, γ ₂]. Учитывая симметрию матрицы С, мы приходим к следующей задаче оптимизации: найти

Поскольку все λ _s лежат на отрезке [ γ ₁, γ ₂], то расширяя область, по которой берется максимум, мы получим, что

Полученная огрубленная задача имеет более простое решение. Кроме того, при решении такой задачи не используется информация о конкретном расположении собственных значений λ _s на отрезке [ γ ₁, γ ₂], а учитываются лишь границы этого отрезка. Такой подход позволяет построить набор оптимальных параметров для матриц произвольной структуры.
Перейдем к решению указанной огрубленной задачи оптимизации.
Положим

и заметим, что полином P(t) удовлетворяет условию нормировки Р(0) = 1. С помощью замены переменной

мы отобразим отрезок γ ₁ ≤ t ≤ γ ₂ в отрезок -1 ≤ S ≤ 1, причем точка t = 0 переходит в точку S = S₀ = 1 / ρ ₀ > 1.
При такой замене рассматриваемая задача оптимизации переходит в следующую задачу: среди всех полиномов (S) степени k , удовлетворяющих условию нормировки (1 / ρ ₀) = 1, найти такой, для которого минимален.
Таким полиномом, как известно, является полином Чебышева

Так как max , то

причем , где .
Для вычисления оптимального набора параметров будем исходить из равенства

(мы учли, что ). Приравняем корни полиномов, стоящих в левой и в правой частях этого равенства. Так как полином P_k(t) имеет корни t_j = 1 / τ _j (j = 1, 2. k ), а полином T_k(S) имеет корни

то, учитывая, что , получим (j = 1, 2, . k; S_j определены выше).
Итак, оптимальными значениями итерационных параметров будут значения

Итерационный процесс с указанным оптимальным набором параметров называется чебышевским.
Мы приходим к следующей теореме.
Теорема 6.4. Если матрицы А и В симметричны и положительно определены и если γ ₁B ≤ А ≤ γ ₂В, то чебышевский итерационный процесс сходится и для погрешности Z_k после выполнения k итераций справедлива оценка

где при .
Если в качестве условия окончания процесса взять для заранее заданной ε -точности требование ||Z_k||_В ≤ ε ||Z₀||_В, то из теоремы 6.4 получается для числа итераций k следующая оценка: k ≥ k₀( ε) = l n ( ε /2) / ln ρ₁ . Сравнивая эту оценку с установленной выше оценкой числа итераций для метода простой итерации ≥ ₀( ε) = l n ε / ln ρ₀ , мы получим, при условии, что величина ξ = γ ₂ / γ ₁ мала, что k₀( ε) ≈ l n ( 2/ε ) / (2) , ₀( ε) ≈ l n (1/ε) / (2ξ) . Сравнение этих оценок указывает на преимущество чебышевского метода (в случае, когда величина ξ = γ ₂ / γ ₁ мала).
Описанный нами чебышевский метод известен еще с начала 50-х годов. Иногда его называют методом Ричардсона.
Следует отметить, что мы изучили этот метод для идеального вычислительного процесса с бесконечным числом знаков, в то время как на ЭВМ вычисления ведутся с конечным числом знаков, в связи с чем имеются числа, являющиеся машинной бесконечностью М _∞ и машинным нулем. Если в процессе вычислений на ЭВМ появляется число М, превосходящее М _∞ , то происходит аварийный останов машины (авост).
С точки зрения идеального вычислительного процесса значения итерационных параметров τ _j можно упорядочить как угодно (любым из k! способов). Любые две последовательности итерационных параметров < τ _j> с точки зрения идеального вычислительного процесса эквивалентны, ибо для них требуемая ε -точность достигается за одно и то же число итераций.
Но при вычислении на ЭВМ различные последовательности параметров < τ _j> не эквивалентны. Для одних последовательностей значений < τ _j> может произойти аварийный останов машины вследствие роста промежуточных значений. Для других последовательностей значений < τ _j> аварийного останова машины не происходит, но в связи с немонотонным характером стремления к нулю погрешности Z _k , т.е. вследствие того, что норма матрицы Е — τ _jC перехода от (j — 1)-й итерации к j-й может быть больше единицы, для этой погрешности не справедлива установленная нами для идеальной ситуации оценка.
Вследствие указанных обстоятельств возникает теоретическая проблема — указать такой наилучший закон упорядочения значений < τ _j>, при котором для чебышевского метода было бы наименьшим влияние ошибок округления.
Исчерпывающее решение этой проблемы можно найти в книге Самарский А. А. Теория разностных схем. — М.: Наука, 1977. С. 572 и далее.