Системы линейных уравнений. Система m линейных уравнений с n переменными в общем виде записывается следующим образом:
Система m линейных уравнений с n переменными в общем виде записывается следующим образом:
где xj – переменные, aij, bi – константы, 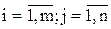
При этом величины aij (те константы, которые умножаются на переменные) принято называть коэффициентами при переменных, а правые части уравнений bi (те константы, которые не умножаются на переменные) — свободными членами.
Более кратко ту же систему можно записать в виде:
Отметим, что в последней записи тоже записана именно система уравнений, хотя на первый взгляд создается впечатление, что уравнение только одно (запись 
Решением такой системы называют совокупность n числовых значений переменных xj, при подстановке которых в систему каждое уравнение обращается в истинное равенство.
Систему уравнений называют совместной, если она имеет хотя бы одно решение (т.е. хотя бы один такой набор из n чисел), и несовместной, если она не имеет решений.
Совместную систему уравнений называют определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Например, рассмотрим систему уравнений 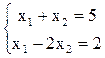
Чтобы решить эту систему, вычтем из верхнего уравнения нижнее. Получим 3х2 = 3. Отсюда х2 = 1; и из любого уравнения х1 = 4. Таким образом, эта система имеет только одно решение – (4; 1). Это означает, что она — совместная и определенная.
Рассмотрим другую систему: 
Приведем пример несовместной системы: 
Две системы уравнений называются равносильными, или эквивалентными, если они имеют одно и то же множество решений.
Запишем систему линейных уравнений в общем виде в матричной форме. Обозначим:
Кроме того, для решения систем линейных уравнений используют также понятие расширенной матрицы системы, которую получают, приписав к матрице системы справа столбец свободных членов:
Задумаемся, что будет, если подвергнуть расширенную матрицу системы рассмотренным ранее элементарным преобразованиям строк матрицы:
а) отбрасыванию нулевых строк;
б) умножению всех элементов строки на число, отличное от нуля;
в) изменению порядка строк;
г) прибавлению к каждому элементу строки соответствующих элементов другой строки, умноженных на любое число.
Применительно к системе уравнений они сведутся к умножению обеих частей уравнений на одинаковые числа, сложению уравнений друг с другом и перестановке уравнений местами (ну а нулевая строка означает, что соответствующее уравнение вообще исключено из системы). Таким образом, применяя к системе уравнений элементарные преобразования строк, мы получим равносильную систему.
Столбцы матрицы системы тоже можно менять местами. По сути это сведется к перемене местами слагаемых в уравнениях. Впоследствии следует не забыть, что соответствующие переменные поменялись местами (т.е. при умножении преобразованной матрицы на столбец переменных последний тоже надо изменить).
Дата добавления: 2015-10-06 ; просмотров: 961 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Система m линейных алгебраических уравнений с n переменными
Системой m линейных уравнений с n неизвестными называется система вида
где aij и bi (i=1,…,m; b=1,…,n) – некоторые известные числа, а x1,…,xn – неизвестные. В обозначении коэффициентов aij первый индекс iобозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.
Коэффициенты при неизвестных будем записывать в виде матрицы 
Числа, стоящие в правых частях уравнений, b1,…,bm называются свободными членами.
Совокупность n чисел c1,…,cn называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c1,…,cn вместо соответствующих неизвестных x1,…,xn.
Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:
- Система может иметь единственное решение.
- Система может иметь бесконечное множество решений. Например,
. Решением этой системы является любая пара чисел, отличающихся знаком.
- И третий случай, когда система вообще не имеет решения. Например,
, если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.
Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.
Рассмотрим способы нахождения решений системы.
МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:
Рассмотрим матрицу системы 
т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.
Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A -1 , обратную матрице A: 
Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A -1 B.
Примеры. Решить системы уравнений.

Найдем матрицу обратную матрице A.

Таким образом, x = 3, y = – 1.
Решите матричное уравнение: XA+B=C, где
Выразим искомую матрицу X из заданного уравнения.
Найдем матрицу А -1 .
Решите матричное уравнение AX+B=C, где
Из уравнения получаем 
Следовательно,
Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:
Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,
называется определителем системы.
Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов
Тогда можно доказать следующий результат.
Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём
Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A11 элемента a11, 2-ое уравнение – на A21 и 3-е – на A31:
Сложим эти уравнения:
Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца

Далее рассмотрим коэффициенты при x2:
Аналогично можно показать, что и 
Наконец несложно заметить, что
Таким образом, получаем равенство: 
Следовательно, 
Аналогично выводятся равенства 

Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.
Примеры. Решить систему уравнений

Решите систему уравнений при различных значениях параметра p:
Система имеет единственное решение, если Δ ≠ 0.


- При
- При p = 30 получаем систему уравнений
которая не имеет решений.
- При p = –30 система принимает вид
и, следовательно, имеет бесконечное множество решений x=y,y Î R.
Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.
Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x1. Для этого второе уравнение разделим на а21 и умножим на –а11, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а31 и умножим на –а11, а затем сложим с первым. В результате исходная система примет вид:
Теперь из последнего уравнения исключим слагаемое, содержащее x2. Для этого третье уравнение разделим на 

Отсюда из последнего уравнения легко найти x3, затем из 2-го уравнения x2 и, наконец, из 1-го – x1.
При использовании метода Гаусса уравнения при необходимости можно менять местами.
Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:
и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.
К элементарным преобразованиям матрицы относятся следующие преобразования:
- перестановка строк или столбцов;
- умножение строки на число, отличное от нуля;
- прибавление к одной строке другие строки.
Примеры: Решить системы уравнений методом Гаусса.

Вернувшись к системе уравнений, будем иметь
Выпишем расширенную матрицу системы и сведем ее к треугольному виду.
Вернувшись к системе уравнений, несложно заметить, что третье уравнения системы будет ложным, а значит, система решений не имеет.
Разделим вторую строку матрицы на 2 и поменяем местами первый и третий столбики. Тогда первый столбец будет соответствовать коэффициентам при неизвестной z, а третий – при x.
Вернемся к системе уравнений.
Из третьего уравнения выразим одну неизвестную через другую и подставим в первое.
Таким образом, система имеет бесконечное множество решений.
Системы n линейных уравнений с n переменными
Метод обратной матрицы и формулы Крамера.
Пусть число уравнений совпадает с число переменных m=n. В этом случае матрица А=(аij)nxn является квадратной. Назовем определитель этой матрицы ∆ =│А│ определителем системы.
Предположим, что матрица А невырожденная, т.е. её определитель │А│≠0. В этом случае существует обратная матица А — 1 .
Умножим обе части матричного уравнения (3.2.2) слева на матрицу А -1 . Получаем А -1 АХ= А -1 В, но А -1 А=Е, следовательно, ЕХ= А -1 В. Но ЕХ=Х (свойства матриц). И сказанного получаем решение матричного уравнения
Х= А -1 В(3.2.3)

Формулы (3.4) называются формулами Крамера.
Доказательство
Подставим обратную матрицу А -1 = 






— = 
учитывая, что │А│= ∆, после умножения матриц получаем:




— = 

xj= 


Пример.Решить систему уравнений

а) матричным способом; б) по формулам Крамера.
Решение.






А= -2 3 -3 ; Х= х2 ; В= -5
В матричной форме решение имеет вид Х=А -1 В. Найдем обратную матрицу в соответствии с алгоритмом:


Обратная матрица существует.
2. Составляем матрицу из алгебраических дополнений определителя матрицы.




3.Присоединённая матрица имеет вид


4. А -1 = 
Подставим А -1 в (3.2.5)










Х2 = 

Х3 -1 10 7 10 -8-50+70 3
б) Определитель системы ∆=4






10 -4 5 3 10 5 3 -4 10
По формулам Крамера (3.2.4) определяем
х1= 




В конце целесообразно сделать проверку, подставив найденные значения Хj в уравнения системы.
Решение систем матричным способом или по правилу Крамера имеет ряд недостатков:
1.Область применения этих способов ограничена условием m=n (число уравнений совпадает с числом неизвестных). В то же время решение практических задач (в экономике в том числе), как правило, приводит к необходимости решения систем, когда число неизвестных n достаточно велико, и m≠n.
2.При выполнении условия m=n матрица системы должна быть невырожденной (│А│=∆≠0).
3.Даже при выполнении 2-го условия (m=n, ∆≠0) вычисление определителей и отыскание обратной матрицы связаны с громоздкими вычислениями.
Метод Гаусса
Рассмотрим решение системы (3.2.1) mлинейных уравнений с nпеременными в общем виде.
Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Предположим, что в системе (3.2.1) коэффициент при переменной х1 в первом уравнении а11≠0 (если это не так, то перестановкой уравнений местами добьёмся того, чтобы а11≠0 ).
Шаг 1. Умножая первое уравнение на подходящие числа и прибавляя полученные уравнения соответственно ко второму, третьему,…, m-му уравнению системы (3.2.1) , исключаем переменную х1 из всех последующих уравнений, начиная со второго. В результате получаем систему

где буквой с верхним индексом «(1)» обозначены новые коэффициенты, полученные после шага 1.


Назовем 1-е уравнение разрешающим,а коэффициент а11 — разрешающимкоэффициентом.
Умножим 1-е уравнение системы на такое «удобное» число λ, чтобы после этого, прибавив 1-е уравнение к i-му уравнению, переменная х1 в i-ом уравнении не содержалась. При этом само 1-е уравнение сохраняется в системе на своем месте.

Из (3.2.7) следует, что новые коэффициенты при xj в i-ом уравнении имеют вид a’ij = λa1j+aij, j=1,n, чтобы x1 не входило в i-ое уравнение, число λ должно быть таким, чтобы λa11+ai1=0, откуда λ= — 
 |
Для пересчета коэффициентов и свободного члена по формулам (3.2.8) удобно использовать «правило прямоугольника»:



aij-разрешаемый (пересчитываемый) элемент
Чтобы пересчитать коэффициент, следует от произведения разрешаемого и разрешающего элементов вычесть произведение сопутствующих элементов и полученную разность разделить на разрешающий элемент.
Шаг 2.Временно 1-е уравнение исключаем. Если а (1) 22≠0 (всегда можно добиться), то второе уравнение выбираем в качестве разрешающего. Со 2-ым уравнением системы поступим так же, как и на 1-м шаге, исключаем из всех уравнений, начиная с 3-го уравнения, переменную х2.
Продолжая процесс последовательного исключения переменных х3, х4, …, хr-1, после (r-1)-го шага получаем систему

Число ноль в последних m – r уравнениях означает, что их левые частиимеют вид: 0*х1 + 0*х2 + … + 0*хn. Если хотя бы одно из чисел b (r-1) r+1,… b (r-1) m не равно нулю, то соответствующее равенство противоречиво и система (3.2.9) несовместна.
Таким образом, для любой совместной системы числа b (r-1) r+1,… b (r-1) m в системе равны нулю. В этом случае последние m – r уравнений в системе (3.2.9) являются тождествами и их можно не принимать во внимание при решение системы (3.2.1). Очевидно, что после отбрасывания «лишних» уравнений возможны два случая: а) число уравнений системы (3.2.1) равно числу переменных, т.е. r = n (в этом случае система (3.2.9) имеет треугольный вид); б) r r n. Таким образом, совместная система m линейных уравнений с n переменными (m r n , где r≤m.
Приведенная схема не означает, что для решения системы (3.2.1) в общем случае необходимо вычислять отдельно, а затем сравнивать ранги матрицы системы А и расширенной матрицы (А/В). Достаточно сразу применить метод Гаусса.
Метод Гаусса по сравнению с другими методами (в частности, приведенными в параграфе) имеет следующие достоинства:
· значительно менее трудоемкий;
· позволяет однозначно установить, совместна система или нет, а в случае совместности найти ее решения (единственное или бесконечное множество);
· дает возможность найти максимальное число линейно независимых уравнений (ранг матрицы системы).
Пример. Решить систему уравнений.




Для удобства поменяем местами 1-ю и 2-ю строки, и первое уравнение будем считать разрешающим с разрешающим элементом а11≠0. Матрица (А/В) перейдет в эквивалентную



1 шаг.Под разрешающим элементом записываем нули, а остальные элементы пересчитываем (например, по правилу прямоугольника). Получаем:
 |  |

Две одинаковые строки в матрице означают, что в системе после преобразований получены 2 одинаковых уравнения. Следовательно, одно из одинаковых уравнений (одну из одинаковых строк) можно отбросить. Получена матрица






Минор = -5 ≠ 0. Следовательно, ранг А/ В = 2
Больше шагов не требуется.
В системе две переменные являются базисными. Это могут быть переменные х1, х2. Тогда остальные переменные х3, х4 можно считать свободными,через которые можно выразить базисные переменные. Из последней матрицы следует:



х1 = — 6 — 
Найдем базисное решение, полагая, что свободные переменные х3=х4=0. Тогда х1 = 

Получено базисное решение Χ = ( 
Приняв за базисные переменные любую другую пару переменных, можно получить другие базисные решения. Число базисных решений
N = C 2 4 = 
http://toehelp.ru/theory/math/lecture14/lecture14.html
http://megaobuchalka.ru/3/29052.html
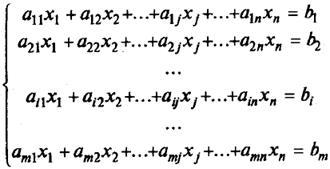



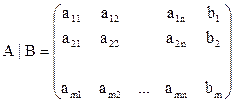

 . Решением этой системы является любая пара чисел, отличающихся знаком.
. Решением этой системы является любая пара чисел, отличающихся знаком. , если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.
, если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.





















 которая не имеет решений.
которая не имеет решений. и, следовательно, имеет бесконечное множество решений x=y,y Î R.
и, следовательно, имеет бесконечное множество решений x=y,y Î R.









