Система нормальных уравнений линейная регрессия

ML | Нормальное уравнение в линейной регрессии

Нормальное уравнение — это аналитический подход к линейной регрессии с функцией наименьших квадратов. Мы можем напрямую узнать значение θ без использования градиентного спуска . Следование этому подходу является эффективным и экономящим время вариантом при работе с набором данных с небольшими функциями.

Нормальное уравнение выглядит следующим образом:

В приведенном выше уравнении
θ: параметры гипотезы, которые определяют ее наилучшим образом.
X: введите значение функции каждого экземпляра.
Y: выходное значение каждого экземпляра.

Математика За уравнением —

Учитывая гипотезу функции

где,
N: нет. функций в наборе данных.
х ₀ : 1 (для векторного умножения)

Обратите внимание, что это скалярное произведение между значениями θ и x. Так что для удобства решения мы можем написать это как:

Мотивом в линейной регрессии является минимизация функции стоимости :

где,
x i : входное значение i ih учебного примера.
м: нет. учебных экземпляров
н: нет. функций набора данных
y i : ожидаемый результат i- го экземпляра

Представим функцию стоимости в векторной форме.

мы проигнорировали 1 / 2m здесь, поскольку это не будет иметь никакого значения в работе. Использовался для математического удобства при расчете градиентного спуска. Но это больше не нужно здесь.

х I _J: значение J функции Ih в я Ih примере обучения.

Это может быть дополнительно уменьшено до
Но каждая остаточная стоимость возводится в квадрат. Мы не можем просто возвести в квадрат вышеприведенное выражение. Так как квадрат вектора / матрицы не равен квадрату каждого из его значений. Таким образом, чтобы получить квадратное значение, умножьте вектор / матрицу на ее транспонирование. Итак, окончательное уравнение получено

Следовательно, функция стоимости

Итак, теперь получим значение θ, используя производную

Итак, это окончательно выведенное нормальное уравнение с θ, дающим минимальное значение стоимости.

Уравнение регрессии

Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии

В сервисе для нахождения параметров регрессии используется МНК. Система нормальных уравнений для линейной регрессии: 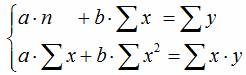. Также можно получить ответ, используя матричный метод. см. также Статистические функции в Excel

Уравнение парной регрессии относится к уравнению регрессии первого порядка. Если эконометрическая модель содержит только одну объясняющую переменную, то она имеет название парной регрессии. Уравнение регрессии второго порядка и уравнение регрессии третьего порядка относятся к нелинейным уравнениям регрессии.

Пример . Осуществите выбор зависимой (объясняемой) и объясняющей переменной для построения парной регрессионной модели. Дайте графическое изображение регрессионной зависимости. Определите теоретическое уравнение парной регрессии. Оцените адекватность построенной модели (интерпретируйте R-квадрат, показатели t-статистики, F-статистики).
Решение будем проводить на основе процесса эконометрического моделирования.
1-й этап (постановочный) – определение конечных целей моделирования, набора участвующих в модели факторов и показателей, их роли.
Спецификация модели — определение цели исследования и выбор экономических переменных модели.
Ситуационная (практическая) задача. По 10 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от удельного веса рабочих высокой квалификации в общей численности рабочих x (в %).
2-й этап (априорный) – предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации и исходных допущений, в частности относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих в виде ряда гипотез.
Уже на этом этапе можно говорить о явной зависимости уровня квалификации рабочего и его выработкой, ведь чем опытней работник, тем выше его производительность. Но как эту зависимость оценить?
Парная регрессия представляет собой регрессию между двумя переменными – y и x , т. е. модель вида:

Как решить линейную регрессию с помощью линейной алгебры

Дата публикации 2018-03-05

Линейная регрессия — это метод моделирования отношений между одной или несколькими независимыми переменными и зависимой переменной.

Это основной продукт статистики, который часто считается хорошим начальным методом машинного обучения. Это также метод, который может быть переформулирован с использованием матричной записи и решен с использованием матричных операций.

В этом уроке вы узнаете матричную формулировку линейной регрессии и способы ее решения с использованием методов прямой и матричной факторизации.

После завершения этого урока вы узнаете:

• Линейная регрессия и переформулировка матрицы с помощью нормальных уравнений.
• Как решить линейную регрессию с использованием декомпозиции матрицы QR.
• Как решить линейную регрессию, используя SVD и псевдообратную.

Обзор учебника

Этот урок разделен на 6 частей; они есть:

1. Линейная регрессия
2. Матричная формулировка линейной регрессии
3. Набор данных линейной регрессии
4. Решить напрямую
5. Решить с помощью QR-разложения
6. Решить через разложение по сингулярному значению

Линейная регрессия

Линейная регрессия — это метод моделирования отношений между двумя скалярными значениями: входной переменной x и выходной переменной y.

Модель предполагает, что y является линейной функцией или взвешенной суммой входной переменной.

Или указано с коэффициентами.

Модель также можно использовать для моделирования выходной переменной с учетом нескольких входных переменных, называемых многомерной линейной регрессией (ниже для удобства чтения были добавлены скобки).

Цель создания модели линейной регрессии состоит в том, чтобы найти значения для значений коэффициента (b), которые минимизируют ошибку в прогнозировании выходной переменной y.

Матричная формулировка линейной регрессии

Линейная регрессия может быть задана с использованием матричной записи; например:

Или без точечной записи.

Где X — входные данные, а каждый столбец — объект данных, b — вектор коэффициентов, а y — вектор выходных переменных для каждой строки в X.

Переформулированная задача превращается в систему линейных уравнений, в которой значения вектора b неизвестны. Система такого типа упоминается как переопределенная, потому что существует больше уравнений, чем неизвестных, то есть каждый коэффициент используется в каждой строке данных.

Это сложная проблема для решения аналитически, потому что есть несколько противоречивых решений, например, несколько возможных значений для коэффициентов. Кроме того, все решения будут иметь некоторую ошибку, потому что нет линии, которая будет проходить почти через все точки, поэтому подход к решению уравнений должен быть в состоянии справиться с этим.

Как правило, это достигается путем нахождения решения, в котором значения b в модели минимизируют квадратичную ошибку. Это называется линейным методом наименьших квадратов.

Эта формулировка имеет уникальное решение, если входные столбцы независимы (например, некоррелированы).

Мы не всегда можем получить ошибку e = b — Ax до нуля. Когда e равно нулю, x является точным решением Ax = b. Когда длина е настолько мала, насколько это возможно, это решение наименьших квадратов.

В матричной записи эта проблема формулируется с использованием так называемого нормального уравнения:

Это может быть переупорядочено, чтобы указать решение для b как:

Это может быть решено напрямую, хотя наличие обратной матрицы может быть численно сложным или нестабильным.

Набор данных линейной регрессии

Чтобы изучить матричную формулировку линейной регрессии, давайте сначала определим набор данных как контекст.

Мы будем использовать простой 2D-набор данных, в котором данные легко визуализировать в виде точечной диаграммы, а модели легко представить в виде линии, которая пытается соответствовать точкам данных.

Приведенный ниже пример определяет матричный набор данных 5 × 2, разбивает его на компоненты X и y и строит набор данных как график рассеяния.

При запуске примера сначала печатается определенный набор данных.

Затем создается точечная диаграмма набора данных, показывающая, что прямая линия не может точно соответствовать этим данным.

Решить напрямую

Первый подход — попытаться решить проблему регрессии напрямую.

То есть, учитывая X, каков набор коэффициентов b, который при умножении на X даст y. Как мы видели в предыдущем разделе, нормальные уравнения определяют, как вычислять b напрямую.

Это можно вычислить непосредственно в NumPy, используя функцию inv () для вычисления обратной матрицы.

После того как коэффициенты рассчитаны, мы можем использовать их для прогнозирования результатов с учетом X.

Объединяя это с набором данных, определенным в предыдущем разделе, полный пример приведен ниже.

При выполнении примера выполняется вычисление и выводится вектор коэффициента b.

Затем создается точечная диаграмма набора данных с линейным графиком для модели, показывающим разумное соответствие данным

Проблема с этим подходом — обратная матрица, которая является вычислительно дорогой и численно нестабильной. Альтернативный подход заключается в использовании матричной декомпозиции, чтобы избежать этой операции. Мы рассмотрим два примера в следующих разделах.

Решить с помощью QR-разложения

QR-разложение — это подход к разбивке матрицы на составляющие ее элементы.

Где A — матрица, которую мы хотим разложить, Q — матрица с размером m x m, а R — верхняя треугольная матрица с размером m x n.

QR-разложение является популярным подходом для решения линейного уравнения наименьших квадратов.

Переходя ко всему выводу, коэффициенты могут быть найдены с использованием элементов Q и R следующим образом:

Подход все еще включает матричную инверсию, но в этом случае только на более простой R-матрице.

QR-разложение можно найти с помощью функции qr () в NumPy. Расчет коэффициентов в NumPy выглядит следующим образом:

Связав это с набором данных, полный пример приведен ниже.

Выполнение примера сначала печатает решение коэффициента и наносит на график данные с моделью.

Подход QR-разложения более эффективен в вычислительном отношении и более численно стабилен, чем прямой расчет нормального уравнения, но не работает для всех матриц данных.

Решить через разложение по сингулярному значению

Разложение по сингулярному значению, или сокращенно SVD, — это метод матричной декомпозиции, такой как QR-декомпозиция.

Где A — вещественная матрица nxm, которую мы хотим разложить, U — матрица amxm, Sigma (часто представляемая заглавной греческой буквой Sigma) — диагональная матрица mxn, а V ^ * — сопряженная транспонирование матрицы nxn, где * — верхний индекс.

В отличие от разложения QR, все матрицы имеют разложение SVD. В качестве основы для решения системы линейных уравнений для линейной регрессии SVD является более устойчивым и предпочтительным подходом.

После разложения коэффициенты могут быть найдены путем вычисления псевдообращения входной матрицы X и умножения ее на выходной вектор y.

Где псевдообратный рассчитывается следующим образом:

Где X ^ + — псевдообратная X, а + — верхний индекс, D ^ + — псевдообратная диагональная матрица Sigma, а V ^ T — транспонирование V ^ *.

Инверсия матриц не определена для матриц, которые не являются квадратными. […] Когда A имеет больше столбцов, чем строк, то решение линейного уравнения с использованием псевдообратного представления дает одно из многих возможных решений.

Мы можем получить U и V из операции SVD. D ^ + можно рассчитать, создав диагональную матрицу из Sigma и вычислив обратную величину каждого ненулевого элемента в Sigma.

Мы можем вычислить SVD, затем псевдообратную вручную. Вместо этого NumPy предоставляет функцию pinv (), которую мы можем использовать напрямую.

Полный пример приведен ниже.

При выполнении примера печатается коэффициент и данные отображаются красной линией, показывающей прогнозы из модели.

Фактически, NumPy предоставляет функцию для замены этих двух шагов в функции lstsq (), которую вы можете использовать напрямую.

расширения

В этом разделе перечислены некоторые идеи по расширению учебника, которые вы, возможно, захотите изучить.

• Реализация линейной регрессии с использованием встроенной функции lstsq () NumPy
• Проверьте каждую линейную регрессию на своем собственном маленьком вымышленном наборе данных.
• Загрузите набор табличных данных и протестируйте каждый метод линейной регрессии и сравните результаты.

Если вы исследуете какое-либо из этих расширений, я хотел бы знать.

Дальнейшее чтение

Этот раздел предоставляет больше ресурсов по теме, если вы хотите углубиться.

книги

• Раздел 7.7. Наименьшие квадраты приближенных решений.Руководство по линейной алгебре, 2017
• Раздел 4.3 Аппроксимации наименьших квадратов,Введение в линейную алгебру, Пятое издание, 2016.
• Лекция 11, Проблемы наименьших квадратов,Численная линейная алгебра, 1997.
• Глава 5, Ортогонализация и наименьшие квадраты,Матричные вычисления2012.
• Глава 12, Сингулярное значение и разложение Джордана,Линейная алгебра и матричный анализ для статистики2014
• Раздел 2.9. Псевдообращение Мура-Пенроуза.Глубокое обучение, 2016
• Раздел 15.4 Генеральные линейные наименьшие квадраты,Численные рецепты: искусство научных вычисленийТретье издание, 2007.

статьи

Учебники

Резюме

В этом руководстве вы обнаружили матричную формулировку линейной регрессии и способы ее решения с использованием методов прямой и матричной факторизации.

В частности, вы узнали:

• Линейная регрессия и переформулировка матрицы с помощью нормальных уравнений.
• Как решить линейную регрессию с использованием декомпозиции матрицы QR.
• Как решить линейную регрессию, используя SVD и псевдообратную.

У вас есть вопросы?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.