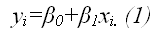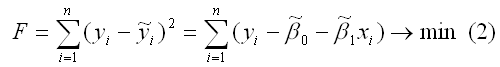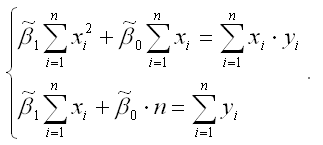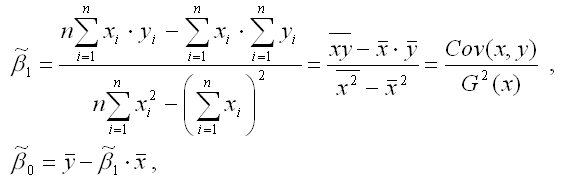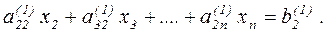Система нормальных уравнений получается из условий минимизации

Система нормальных уравнений и явный вид ее решения при оценивании методом наименьших квадратов линейной модели парной регрессии

Предположим, что в ходе регрессионного анализа была установлена линейная взаимосвязь между исследуемыми переменными х и у, которая описывается моделью регрессии вида:

В результате оценивания данной эконометрической модели определяются оценки неизвестных коэффициентов. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).

Метод наименьших квадратов позволяет получить такие оценки параметров β₀и β₁, при которых сумма квадратов отклонений фактических значений результативного признака y от расчетных (теоретических) y˜ минимальна:

В процессе минимизации функции (1) неизвестными являются только значения коэффициентов β₀ и β₁, потому что значения результативной и факторной переменных известны из наблюдений. Для определения минимума функции двух переменных вычисляются частные производные этой функции по каждому из оцениваемых параметров и приравниваются к нулю. Результатом данной процедуры будет стационарная система уравнений для функции (2):

.

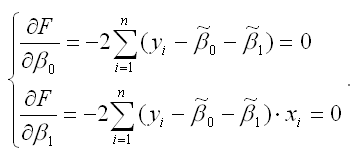
Если разделить обе части каждого уравнения системы на (-2), раскрыть скобки и привести подобные члены, то получим систему нормальных уравнений для функции регрессии вида yi=β₀+β₁xi:

Если решить данную систему нормальных уравнений, то мы получим искомые оценки неизвестных коэффициентов модели регрессии β₀ и β₁:

y – среднее значение зависимой переменной;

x – среднее значение независимой переменной;

xy – среднее арифметическое значение произведения зависимой и независимой переменных;

G 2 (x) – дисперсия независимой переменной;

Gcov (x, y) – ковариация между зависимой и независимой переменными.

Таким образом, явный вид решения системы нормальных уравнений может быть записан следующим образом:

Описание метода вычисления коэффициентов нормальных уравнений.

Аналогичные уравнения можно получить, применяя описанные выше операции по отношению к переменным С₂ ,…,С_m . Эти уравнения образуют систему нормальных уравнений:

где коэффициенты a_{k l} и величины b_k (k, l = 1, 2,…, m) определяются выражениями

Уравнения (5) представляют собой систему линейных алгебраических уравнений.

Преимущество использования линейного представления аппроксимирующей функции j (x) состоит в том, что в этом случае однозначно решается вопрос о минимуме величины J. Действительно, если решение системы линейных уравнений (9) существует, то оно единственно, поэтому необходимые условия являются в данном случае и достаточными условиями минимума функции J(С₁, С₂ ,…, С_m).

5)Описание метода определения параметров аппроксимирующей функции (решение системы нормальных уравнений).

Для решения системы нормальных уравнений был выбран метод Гаусса.

Один из возможных способов минимизации критерия аппроксимации предполагает решение системы нормальных уравнений. При выборе в качестве аппроксимирующей функции линейной функции искомых параметров нормальные уравнения представляют собой систему линейных алгебраических уравнений.

Систему n линейных уравнений общего вида (где через x_k обозначены искомые параметры С_k аппроксимирующей функции)

можно записать посредством матричных обозначений в следующем виде:

Квадратная матрица A называется матрицей системы, вектор X – вектором-столбцом неизвестных системы, а вектор B – вектором-столбцом свободных членов.

В матричном представлении исходная система линейных уравнений примет вид

Решение системы линейных уравнений сводится к отысканию значений элементов вектора-столбца (x_i), называемых корнями системы. Для получения единственного решения системы входящие в нее n уравнений должны быть линейно независимыми. Необходимым и достаточным условием этого является неравенство нулю определителя данной системы, т.е.
det A ¹ 0.

Для решения был выбран метод Гаусса. Согласно этому методу, исходная система линейных уравнений преобразуется путем последовательного исключения неизвестных в эквивалентную систему уравнений, имеющую так называемый «треугольный» вид. Последнее уравнение «тре­угольной» системы содержит лишь одно неизвестное (x_n), предпоследнее – два (x_n, x_n-1) и т.д. Решение полученной системы уравне­ний осуществляется последовательным («снизу вверх») определением x_n из последнего уравнения «треугольной» системы, x_n-1изпредпоследнего и т.д. Применительно к системе уравнений преобразование к «треугольному» виду осуществляется за (n – 1) шагов.

На первом шаге выделяется первое уравнение системы. Это уравнение не преобразуется, и оно объявляется ведущим уравнением. Затем исключается неизвестное x₁ из всех уравнений, кроме веду­щего. Для этого последовательно из каждого уравнения вычитается ведущее уравнение, умноженное на некоторый специально подобранный множитель, позволяющий сделать результирующий коэффициент при x₁ равным нулю. Так, например, для исключения x₁ из второго уравнения

необходимо из него вычесть ведущее уравнение, умноженное на коэффициент q₂₁ = a₂₁ / a₁₁. Действительно, результат вычитания имеет вид

Очевидно, что коэффициент (a₂₁ – q₂₁ a₁₁ ) при x₁ равен ну­лю. Вводя новые обозначения для коэффициентов

k=(2, …, n) ,

и свободного члена

можно переписать уравнение в виде

Аналогичную процедуру можно проделать с третьим уравнением системы. Умножая ведущее уравнение на q₃₁=a₃₁ /a₁₁ и вы­читая результат умножения из третьего уравнения, получим эквива­лентное уравнение

и т.д.

В результате рассмотренного первого шага исходная система уравнений превратится в эквивалентную систему уравнений, причем неизвестное x₁ входит только в первое уравнение:

На втором шаге ведущим объявляется второе уравнение системы и исключается неизвестное x₂ из уравнений с номерами от третьего до последнего. Исключение неизвестного проводится по схеме, описанной в первом шаге. Для исключения x₂ из третьего уравнения системы ведущее уравнение умножается на

и результат умножения вычитается из третьего уравнения, результирующий коэффициент при x₂ будет равен нулю. Для исключения x₂ из четвертого уравнения ведущее уравнение умножается на

и т.д. В результате второго шага (исключения неизвестного x₂) будет получена система урав­нений, также эквивалентная исходной системе:

где введены новые обозначения для коэффициен­тов преобразуемых уравнений. Отметим, что неизвестное x₁ вхо­дит только в первое уравнение, а неизвестное x₂ — в первое и второе уравнения.

На (n—1) шаге исключается неизвестное x_n-1 из последнего n-го уравнения, и в результате система уравнений принимает окончательный «треугольный» вид

Полученная система уравнений эквивалентна исходной системе уравнений. Описанный процесс последовательного исключения неизвестных носит название прямого хода метода Гаусса.

Определим обобщенные формулы для расчета коэффициентов системы в процессе прямого хода метода Гаусса. На i-м шаге неизвестное x_i исключается из всех уравнений с номерами k, где i+1 £ k £ n, при этом ведущее уравнение (с номером i) умножается на

,

и результат умножения вычитается из k-го уравнения. Новые значения коэффициентов (в уравнении с номером k) при неизвестных x_j, (i+1 £ j £ n) равны

новое значение свободного члена

.

Решение треугольной системы уравнений носит название обратного хода метода Гаусса и заключается в последовательном определении всех неизвестных, начиная с последнего x_n. Действительно, из последнего уравнения системы вытекает, что

Значение x_n-1 получается при решении предпоследнего уравнения

.

Так как x_n уже определено, то

Эта процедура применяется последовательно ко всем уравнениям, включая и первое, из которого определяется

Обобщенная формула вычисления x_i имеет вид

В процессе прямого хода метода Гаусса может оказаться, что коэффициент a_ij ( i -1) ведущего уравнения равен нулю. Тогда исключить x_iиз остальных уравнений описанным методом нельзя. Однако уравнения системы можно поменять местами и объявить ведущим то уравнение, у которого коэффициент при неизвестном x_i отличен от нуля. Отметим, что системы, отличающиеся лишь взаимным расположением образующихих уравнений, являются эквивалентными. Перестановка уравнений не только допустима, но часто и полезна для уменьшения погрешности арифметических вычислений. Для уменьшения погрешности вычислений в качестве ведущего обычно выбирается уравнение с максимальным по модулю коэффициентом при x_i. Это уравнение и уравнение с номером i меняют местами, и процесс исключения продолжается обычным образом. Поиск максимального по модулю коэффициента приx_i носит название определение ведущего элемента.

6)Схемы алгоритмов и их описание.

Подпрограмма функции fi

на вход подпрограммы подаются номер функции (k) и элемент Xi из матрицы X

Алгоритм подпрограммы нахождения матриц А и В:

присвоение значения элементу Akl (k-номер столбца, l-номер строки)

выход матрицы A и вектора B

Алгоритм подпрограммы вывода матрицы А:

Алгоритм подпрограммы вывода вектора В:

· Алгоритм подпрограммы решения системы линейных уравнений методом Гаусса:

3.1. Минимизация нормальных форм

Минимальной ДНФ (МДНФ) функции F(X1, . ,Xn) называется ДНФ, реализующая функцию F и содержащая минимальное число символов переменных по сравнению со всеми другими видами ДНФ, реализующими функцию F.

Если для всякого набора = (A1, . An) значений переменных условие G( )=1 влечёт , то функция G называется частью функции F (или функция F накрывает функцию G). Если при этом для некоторого набора = (C1, . Cn) функция G( )=1, то говорят, что функция G накрывает единицу функции F на наборе (или что G накрывает конституенту единицы функции F). Заметим, что конституента единицы функции F есть часть функции F, накрывающая единственную единицу функции F.

Элементарная конъюнкция K называется импликантом функции F, если для всякого набора =(A1, . An) из 0 и 1 условие K( )=1 влечет F( )=1.

Импликант K функции F называется простым, если выражение, получающееся из него выбрасыванием любых множителей, уже не импликант функции F.

Ясно, что всякий импликант функции F есть часть функции F.

Теорема. Всякая функция реализуется дизъюнкцией всех своих простых имликант (ПИ).

Доказательство. Пусть F(X1, . Xn) есть функция, а A = K1 v. v Km – дизъюнкция всех ее простых импликант. Пусть = (A1, . An) – произвольный набор длины N из 0 и 1.

Если A( ) = 1, то найдется дизъюнктивное слагаемое Ki ( ) = 1, что влечет F( ) = 1, ибо Ki есть импликант функции F.

Если F( ) = 1, то в СДНФ для функции F найдется элементарная конъюнкция K, равная на этом наборе единице. Один из простых имликантов Kj функции F получается выбрасыванием некоторых множителей из K и потому Kj( ) = 1, а тогда A( ) = 1.

Следовательно, F = A. Теорема доказана.

Сокращенная ДНФ функции F есть дизъюнкция всех простых импликант функции F. Всякая функция F реализуется своей сокращенной ДНФ. Для всякой функции, не равной тождественно нулю, существует единственная сокращенная ДНФ.

Пусть A и B – произвольные формулы. Из свойств булевых операций вытекают следующие обратимые правила преобразования ДНФ:

1) – полное склеивание (развертывание);

2) – неполное склеивание;

3) – обобщенное склеивание;

4) – поглощение;

5) – идемпотентность ( удаление дублирующих членов).

Теорема ( Квайна ). Если в СДНФ функции F провести все операции неполного склеивания, а затем все операции поглощения и удаления дублирующих членов, то в результате получится сокращения ДНФ функции F.

Доказательство. Пусть имеем сокращенную ДНФ функции F. Проведем все операции развертывания к каждому простому импликанту для получения недостающих переменных в каждом дизъюнктивном слагаемом сокращенной ДНФ. В полученном выражении из нескольких одинаковых дизъюнктивных слагаемых оставим только по одному экземпляру. В результате получим СДНФ функции F. Теперь, исходя из полученной СДНФ, в обратном порядке проведем операции добавления одинаковых дизъюнктивных слагаемых (с помощью правил идемпотентности), неполного склеивания и поглощения. В итоге получим исходную сокращенную ДНФ.

Алгоритм Квайна построения сокращенной ДНФ.

1. Получить СДНФ функции F.

2. Провести все операции неполного склеивания.

3. Провести все операции поглощения.

Пример 1. Построим сокращенную ДНФ для функции, приведенной в таблице 3.1.

0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1

0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1

0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1

0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1

1 1 1 1 0 1 0 0 1 0 1 0 1 1 1 1

1. Строим СДНФ функции F:

. Пронумеруем дизъюнктивные члены в полученной СДНФ в порядке от 1 до 11.

2. Проводим все операции неполного склеивания.

Первый этап склеивания в таблице 3.2.

После первого этапа склеиваний (и возможных поглощений) получаем, что

Пронумеруем дизъюнктивные члены в полученной ДНФ в порядке их следования от 1 до 15.

Второй этап склеиваний в таблице 3.3.

После второго этапа склеиваний и последующих поглощений получаем, что Это и будет сокращенной ДНФ для функции f, ибо дальнейшие склеивания невозможны.