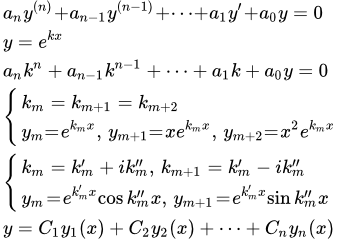Система однородных дифференциальных уравнений с постоянными коэффициентами

Решение линейных однородных дифференциальных уравнений с постоянными коэффициентами

Вид общего решения

Рассмотрим линейное однородное дифференциальное уравнение с постоянными коэффициентами:
(1) .
Его решение можно получить следуя общему методу понижения порядка.

Однако проще сразу получить фундаментальную систему n линейно независимых решений и на ее основе составить общее решение. При этом вся процедура решения сводится к следующим шагам.

Ищем решение уравнения (1) в виде . Получаем характеристическое уравнение:
(2) .
Оно имеет n корней. Решаем уравнение (2) и находим его корни . Тогда характеристическое уравнение (2) можно представить в следующем виде:
(3) .
Каждому корню соответствует одно из линейно независимых решений фундаментальной системы решений уравнения (1). Тогда общее решение исходного уравнения (1) имеет вид:
(4) .

Действительные корни

Рассмотрим действительные корни. Пусть корень однократный. То есть множитель входит в характеристическое уравнение (3) только один раз. Тогда этому корню соответствует решение
.

Пусть – кратный корень кратности p . То есть
. В этом случае множитель входит в характеристическое уравнение (3) p раз:
.
Этим кратным (равным) корням соответствуют p линейно независимых решений исходного уравнения (1):
; ; ; . ; .

Комплексные корни

Рассмотрим комплексные корни характеристического уравнения (3). Выразим комплексный корень через действительную и мнимую части:
.
Поскольку коэффициенты исходного уравнения (1) действительные, то кроме корня имеется комплексно сопряженный корень
.

Пусть комплексный корень однократный. Тогда паре корней соответствуют два линейно-независимых решения уравнения (1):
; .

Пусть – кратный комплексный корень кратности p . Тогда комплексно сопряженное значение также является корнем характеристического уравнения кратности p и множитель входит в разложение на множители (3) p раз:
.
Этим 2 p корням соответствуют 2 p линейно независимых решений:
; ; ; . ;
; ; ; . .

После того как фундаментальная система линейно независимых решений найдена, по формуле (4) получаем общее решение уравнения (1).

Примеры решений задач

Пример 1

Найти общее решение однородного дифференциального уравнения седьмого порядка с постоянными коэффициентами:
.

Ищем решение в виде . Составляем характеристическое уравнение:
.
Преобразуем его:
;
;
.

Рассмотрим корни этого уравнения. Мы получили четыре комплексных корня кратности 2:
; .
Им соответствуют четыре линейно-независимых решения исходного уравнения:
; ; ; .

Также мы имеем три действительных корня кратности 3:
.
Им соответствуют три линейно-независимых решения:
; ; .

Общее решение исходного уравнения имеет вид:
.

Пример 2

Это однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Ищем решение в виде . Составляем характеристическое уравнение:
.
Решаем квадратное уравнение.
.

Мы получили два комплексных корня:
.
Им соответствуют два линейно-независимых решения:
.
Общее решение уравнения:
.

Пример 3

Найти общее решение однородного дифференциального уравнения четвертого порядка с постоянными коэффициентами:
.

Ищем решение в виде . Составляем характеристическое уравнение:
.
Выносим за скобки:
(П3.1) .
Решаем квадратное уравнение :
.
Получили два комплексных корня, которые обозначим как . Тогда . Перепишем характеристическое уравнение (П3.1) в эквивалентном виде:
.
Отсюда видно, что оно имеет два кратных корня кратности 2, и два комплексно сопряженных корня . Кратным корням соответствуют два линейно независимых решения:
;
.
Комплексно сопряженным корням , соответствуют решения
.
Общее решение:
.

Автор: Олег Одинцов . Опубликовано: 29-07-2013 Изменено: 27-10-2020

Линейные системы дифференциальных уравнений с постоянными коэффициентами

Линейные системы дифференциальных уравнений с постоянными коэффициентами

1. Общий вид линейной системы дифференциальных уравнений. Однородные и неоднородные системы. Случаи системы с постоянными коэффициентами

2. Основные свойства линейной системы дифференциальных уравнений

3. Основные способы решения однородной линейной системы

4. Понятие о фундаментальной системе решений однородной линейной системы

5. Построение общего решения однородной линейной системы по фундаментальной системе решений

6. Построение фундаментальной системы решения однородной системы с постоянными коэффициентами методом Эйлера

7. Структура общего решения неоднородной линейной системы

1. Общий вид линейной системы дифференциальных уравнений. Однородные и неоднородные системы. Случаи системы с постоянными коэффициентами

Для решения многих задач математики, физики, техники (задач динамики криволинейного движения; задач электротехники движения; задач электротехники для нескольких электрических цепей; определения состава системы, в которой протекают несколько последовательных химических реакций I порядка; отыскания векторных линий поля и других) нередко требуется несколько функций. Нахождение этих функций может привести к нескольким дифференциальным уравнении ям (ДУ), образующим систему.

Системой ДУ называется совокупность ДУ, каждое из которых содержит независимую переменную, искомые функции и их производные.

Нормальной системой линейных ДУ с действительными коэффициентами, называется система вида:

или более коротко

(2)

где — действительная матрица, а — действительный вектор, определенный при .

Однородной системой линейных уравнений, соответствующей системе (2), называется система уравнений

(3)

Система линейных дифференциальных уравнений с постоянными коэффициентами имеет вид

, (1.1)

где — -мерный вектор, — постоянная квадратная матрица размера .

2. Основные свойства линейной системы дифференциальных уравнений

Теорема 1. Линейная комбинация решений однородной системы (3) также является решением этой системы.

Теорема 2. Разность любых двух решений неоднородной системы уравнений (2) есть решение однородной системы (3).

Сумма любого частного решения неоднородной системы (2) и решения соответствующей однородной системы (3) есть решение неоднородной системы (2).

Теорема 3. Если и — решения систем уравнений

— решение системы уравнений

.

Теорема 4. Пусть () – решение системы уравнений (2), матрица и вектор непрерывны на отрезке . Пусть (где означает норму матрицы : ) и . Тогда для имеет место следующая оценка:

(4)

В частности, для линейной однородной системы (3) имеем оценку ():

(5)

Теорема 5. Пусть матрица системы (2) непрерывна на отрезке и . Тогда решение системы (2) однозначно определяется на отрезке условием

. (6)

Итак, из оценки (5) вытекает единственность решения задачи Коши для линейной системы (2) с непрерывной матрицей .

Следствие 1. Пусть матрица непрерывна на отрезке , тогда и для решения однородной системы (3) имеет место оценка

(7)

Иначе говоря, рост функции ограничен экспонентой.

Следствие 2. Решение однородной линейной системы с непрерывной матрицей тождественно равно нулю, если оно равно нулю в какой либо точке отрезка .

3. Основные способы решения однородной линейной системы

Линейные системы можно интегрировать различными способами, например методом исключения, путем нахождения интегрируемых комбинаций и т. д.

Для интегрирования однородных линейных систем с постоянными коэффициентами применяется метод Эйлера, который будет рассмотрен ниже.

4. Понятие о фундаментальной системе решений однородной линейной системы

Определение 1. Решения однородной системы (3) называются линейно независимыми на отрезке , если в каждой точке векторы линейно независимы.

Пусть задана система решений однородной системы (3), определенных на :

() (8)

Определение 2. Определитель

(9)

называется определителем Вронского системы решений .

Определение 3. Система из решений однородной системы уравнений (3), линейно независимых на отрезке называется фундаментальной.

5. Построение общего решения однородной линейной системы по фундаментальной системе решений

Определение 4. Общим решением линейной системы уравнений (2) называется множество всех решений этой системы.

Теорема 8. Пусть — фундаментальная система решений однородной системы уравнений (3), тогда формула

(15) где — произвольные постоянные, дает общее решение этой системы. Множество всех решений однородной системы уравнений (3) образует -мерное векторное пространство, базисом которого может служить любая фундаментальная система решений.

6. Построение фундаментальной системы решения однородной системы с постоянными коэффициентами методом Эйлера

Система линейных дифференциальных уравнений с постоянными коэффициентами имеет вид

, (1.1)

где — -мерный вектор, — постоянная квадратная матрица размера .

Метод Эйлера заключается в следующем. Решение системы (1.1) ищем в виде

,. (2.1)

Функция (2.1) является решением системы (1.1), если — собственное значение матрицы , а — собственный вектор этой матрицы, соответствующий числу . Если собственные значения матрицы попарно различны и — соответствующие собственные векторы этой матрицы, то общее решение системы уравнений (1.1) определяется формулой

,

где — произвольные числа. Если для кратного собственного значения матрицы имеется столько линейно независимых собственных векторов , какова его кратность, то ему соответствуют линейно независимых решений исходной системы: .

Если для собственного значения кратности имеется только линейно независимых собственных векторов, то решения, соответствующие , можно искать в виде произведения векторного многочлена степени на , т. е. в виде

.

Чтобы найти векторы , надо подставить выражение (2.1) в систему (1). Приравняв коэффициенты в левой и правой частях системы, получим уравнения для нахождения векторов .

Если среди собственных чисел матрицы имеются комплексные числа, то указанным выше методом строится соответствующее такому собственному числу решение системы (1.1) через комплексные функции. Чтобы выразить решение через действительные функции (в случае действительной матрицы ), надо воспользоваться тем, что вещественная и мнимая части комплексного решения, соответствующего собственному числу (), являются линейно независимыми решениями.

7. Структура общего решения неоднородной линейной системы,

Пусть — частное решение неоднородное решение неоднородной системы уравнений (2), а — фундаментальная система решений однородной системы уравнений (3). Тогда формула

, (16)

где — произвольные постоянные, дает общее решение неоднородной системы уравнений (2).

Теорема 9. Пусть на отрезке матрица и вектор непрерывны, и пусть известна фундаментальная система решений для однородной системы уравнений (3). Тогда общее решение неоднородной системы уравнений (2) находится с помощью квадратур.

Доказательство. Пусть — фундаментальная система решений для уравнения (3), тогда

()

или в матричной форме

, (17)

где — матрица, называемая фундаментальной матрицей системы уравнений (3). Определитель фундаментальной матрицы есть определитель Вронского и поэтому отличен от нуля на отрезке : .

Будем искать решение системы уравнений (2) в виде

, (18) где .

Подставляя выражение (18) в (2), получим

. (19)

В силу (17) уравнение (19) примет вид

(20) Так как и матрица непрерывна на , то существует непрерывная на обратная матрица .

Умножая обе части уравнения (20) слева на , получим

,

( 21)

где — произвольный постоянный вектор. Подставляя найденное выражение (21) для в формулу (18), получим

(22) Формула (22) дает общее решение неоднородной системы уравнений (2). Решение задачи Коши для системы (2) задается формулой

.

Метод нахождения решения системы (2) называется методом вариации постоянных или методом неопределенных коэффициентов Лагранжа.

Практически удобно поступать следующим образом: Уравнение (20) в развернутом виде

представляет собой систему линейных уравнений относительно :

,

,

.

Решая эту систему относительно (), получим или

.

Подставляя найденные выражения для в (18) получим общее решение для системы (2).

1. , Рождественский дифференциальные уравнения и основы вариационного исчисления. – М.: Наука, с.

2. и др. Сборник задач по обыкновенным дифференциальным уравнениям: Учеб. пособие для втузов. – М.: Высш. шк., с.: ил.

3. , , Перестюк уравнения: примеры и задачи: Учеб. пособие. – М.: Высш. шк., с.: ил.

Интегрирование однородных линейных систем ДУ
с постоянными коэффициентами. Метод Эйлера

Линейной однородной системой с постоянными коэффициентами называется система дифференциальных уравнений вида

где коэффициенты — постоянные, а — искомые функции от .

Систему (1) можно коротко записать в виде одного матричного уравнения

называется частным решением уравнения (2) в интервале , если выполняется тождество

Система частных решений

(здесь в записи нижний индекс указывает номер решения, а верхний — номер функции в решении) называется фундаментальной на интервале , если ее определитель Вронского

Теорема. Если система частных решений однородного уравнения (2) является фундаментальной, то общее решение этого уравнения имеет вид

где — произвольные постоянные.

Линейные системы можно интегрировать различными способами, рассмотренными ранее, например методом исключения, путем нахождения интегрируемых комбинаций и т.д.

Для интегрирования однородных линейных систем с постоянными коэффициентами применяется также метод Эйлера .

Рассмотрим этот метод в применении к системе трех линейных дифференциальных уравнений:

Решение системы (3) ищем в виде

Подставляя (4) в (3) и сокращая на , получаем систему уравнений для определения и

Система (5) имеет ненулевое решение, когда ее определитель равен нулю,

Уравнение (6) называется характеристическим .

А. Пусть корни и характеристического уравнения — вещественные и различные . Подставив в (5) вместо число и решив систему (5), получим числа и . Затем положим в (5) и получим числа и, наконец, при получим и . Соответственно трем наборам чисел и получим три частных решения

Общее решение системы (3) имеет вид

Пример 1. Решить систему дифференциальных уравнений

Решение. Составляем характеристическое уравнение

Корням соответствуют числа

Выписываем частные решения

Общее решение системы:

Б. Рассмотрим теперь случай, когда корни характеристического уравнения комплексные .

Пример 2. Решить систему линейных однородных дифференциальных уравнений

Решение. Выпишем систему для определения и

имеет корни . Подставляя в (8), получаем два уравнения для определения и

из которых одно является следствием другого (в силу того, что определитель системы (8) равен нулю).

Возьмем , тогда первое частное решение запишется так:

Аналогично, подставляя в (8) корень , найдем второе частное решение:

Перейдем к новой фундаментальной системе решений:

Пользуясь известной формулой Эйлера , из (9), (10) и (11) получаем

Общим решением системы (7) будет

Замечание. Найдя первое частное решение (9), можно было бы сразу написать общее решение системы (7), пользуясь формулами

где и обозначают соответственно действительную и мнимую части комплексного числа , т. е. если , то , .

В. Случай кратных корней.

Пример 3. Решить систему

Решение. Характеристическое уравнение

Решение следует искать в виде

Подставляя (13) в первое уравнение системы (12), получаем

Приравнивая коэффициенты при одинаковых степенях в левой и правой части (14), получаем:

Величины и остаются произвольными. Обозначая их соответственно через и , получаем общее решение системы (12):

Замечание. Легко проверить, что если (13) подставить во второе уравнение системы (12), то получим тот же результат (15). В самом деле, из равенства

получаем два соотношения для определения и через и

Пример 4. Решить задачу Коши для системы линейных дифференциальных уравнений

с начальными условиями .

Решение. Характеристическое уравнение

Корни уравнения (17): . Действительному корню отвечает решение

Подставляя (18) в систему (16) и сокращая на , получаем

откуда . Полагаем, например, , тогда и частное решение (18):

Комплексному корню отвечает решение

подставив которое в (16) и сокращая на , получим

откуда , так что, например, при имеем и частное решение

Корню соответствует решение, комплексно сопряженное решению (20), т.е.

Учитывая (19), (20), (21), получаем общее решение

Выделим, наконец, решение с начальными условиями . Из (22) при имеем

Воспользовавшись формулами Эйлера , окончательно получим