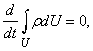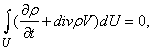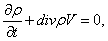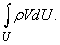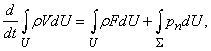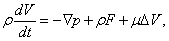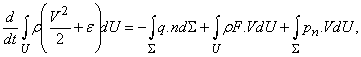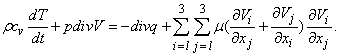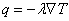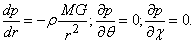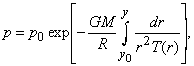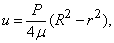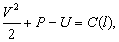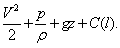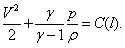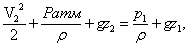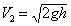Система уравнений для несжимаемой жидкости

Уравнение Навье-Стокса и симуляция жидкостей на CUDA

Привет, Хабр. В этой статье мы разберемся с уравнением Навье-Стокса для несжимаемой жидкости, численно его решим и сделаем красивую симуляцию, работающую за счет параллельного вычисления на CUDA. Основная цель — показать, как можно применить математику, лежащую в основе уравнения, на практике при решении задачи моделирования жидкостей и газов.

Уравнение Навье-Стокса для несжимаемой жидкости

Я думаю каждый хоть раз слышал об этом уравнении, некоторые, быть может, даже аналитически решали его частные случаи, но в общем виде эта задачи остается неразрешенной до сих пор. Само собой, мы не ставим в этой статье цель решить задачу тысячелетия, однако итеративный метод применить к ней мы все же можем. Но для начала, давайте разберемся с обозначениями в этой формуле.

Условно уравнение Навье-Стокса можно разделить на пять частей:

• — обозначает скорость изменения скорости жидкости в точке (его мы и будем считать для каждой частицы в нашей симуляции).
• — перемещение жидкости в пространстве.
• — давление, оказываемое на частицу (здесь — коэффициент плотности жидкости).
• — вязкость среды (чем она больше, тем сильнее жидкость сопротивляется силе, применяемой к ее части), — коэффициент вязкости).
• — внешние силы, которые мы применяем к жидкости (в нашем случае сила будет играть вполне конкретную роль — она будет отражать действия, совершаемые пользователем.

Также, так как мы будем рассматривать случай несжимаемой и однородной жидкости, мы имеем еще одно уравнение: . Энергия в среде постоянна, никуда не уходит, ниоткуда не приходит.

Будет неправильно обделить всех читателей, которые не знакомы с векторным анализом, поэтому заодно и бегло пройдемся по всем операторам, присутствующим в уравнении (однако, настоятельно рекомендую вспомнить, что такое производная, дифференциал и вектор, так как они лежат в основе всего того, о чем пойдет речь ниже).

Начнем мы с с оператора набла, представляющего из себя вот такой вектор (в нашем случае он будет двухкомпонентным, так как жидкость мы будет моделировать в двумерном пространстве):

Оператор набла представляет из себя векторный дифференциальный оператор и может быть применен как к скалярной функции, так и к векторной. В случае скаляра мы получаем градиент функции (вектор ее частных производных), а в случае вектора — сумму частых производных по осям. Главная особенность данного оператора в том, что через него можно выразить основные операции векторного анализа — grad (градиент), div (дивергенция), rot (ротор) и (оператор Лапласа). Стоит сразу же отметить, что выражение не равносильно — оператор набла не обладает коммутативностью.

Как мы увидим далее, эти выражения заметно упрощаются при переходе на дискретное пространство, в котором мы и будем проводить все вычисления, так что не пугайтесь, если на данный момент вам не очень понятно, что же со всем этим делать. Разбив задачу на несколько частей, мы последовательно решим каждую из них и представим все это в виде последовательного применения нескольких функций к нашей среде.

Численное решение уравнения Навье-Стокса

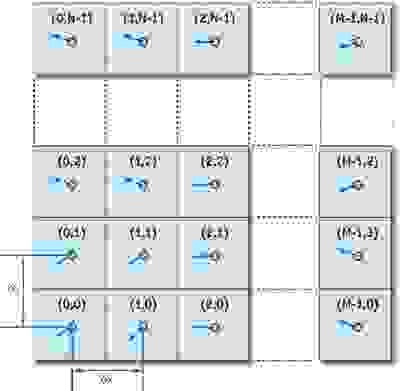
Чтобы представить нашу жидкость в программе, нам необходимо получить математическую репрезентацию состояния каждой частицы жидкости в произвольный момент времени. Самый удобный для этого метод — создать векторное поле частиц, хранящее их состояние, в виде координатной плоскости:

В каждой ячейке нашего двумерного массива мы будем хранить скорость частицы в момент времени , а расстояние между частицами обозначим за и соответственно. В коде же нам будет достаточно изменять значение скорости каждую итерацию, решая набор из нескольких уравнений.

Теперь выразим градиент, дивергенцию и оператор Лапласа с учетом нашей координатной сетки ( — индексы в массиве, — взятие соответствующих компонентов у вектора):

Оператор	Определение	Дискретный аналог
grad
div
rot

Мы можем еще сильнее упростить дискретные формулы векторных операторов, если положим, что . Данное допущение не будет сильно сказываться на точности алгоритма, однако уменьшает количество операций на каждую итерацию, да и в целом делает выражения приятней взгляду.

Перемещение частиц

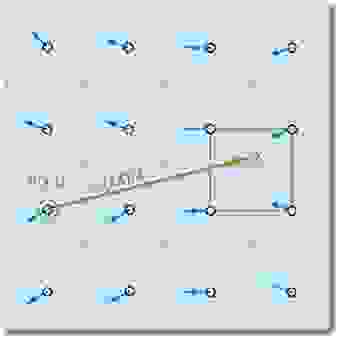
Данные утверждения работают только в том случае, если мы можем найти ближайшие частицы относительно рассматриваемой на данный момент. Чтобы свести на нет все возможные издержки, связанные с поиском таковых, мы будет отслеживать не их перемещение, а то, откуда приходят частицы в начале итерации путем проекции траектории движения назад во времени (проще говоря, вычитать вектор скорости, помноженный на изменение времени, из текущей позиции). Используя этот прием для каждого элемента массива, мы будем точно уверены, что у любой частицы будут «соседи»:

Положив, что — элемент массива, хранящий состояния частицы, получаем следующую формулу для вычисления ее состояния через время (мы полагаем, что все необходимые параметры в виде ускорения и давления уже рассчитаны):

Заметим сразу же, что при достаточно малом и скорости мы можем так и не выйти за пределы ячейки, поэтому очень важно правильно подобрать ту силу импульса, которую пользователь будет придавать частицам.

Чтобы избежать потери точности в случае попадания проекции на границу клеток или в случае получения нецелых координат, мы будем проводить билинейную интерполяцию состояний четырех ближайших частиц и брать ее за истинное значение в точке. В принципе, такой метод практически не уменьшит точность симуляции, и вместе с тем он достаточно прост в реализации, так что его и будем использовать.

Вязкость

. В таком случае итеративное уравнение для скорости примет следующий вид:

Мы несколько преобразуем данное равенство, приведя его к виду (стандартный вид системы линейных уравнений):

где — единичная матрица. Такие преобразования нам необходимы, чтобы в последствии применить метод Якоби для решения нескольких схожих систем уравнений. Его мы также обсудим в дальнейшем.

Внешние силы

Импульс-вектор легко посчитать как разность между предыдущей позицией мыши и текущей (если такая имелась), и здесь как раз-таки можно проявить креативность. Именно в этой части алгоритма мы можем внедрить добавление цветов в жидкость, ее подсветку и т.п. К внешним силам также можно отнести гравитацию и температуру, и хоть реализовать такие параметры несложно, в данной статье рассматривать их мы не будем.

Давление

Давление в уравнении Навье-Стокса — та сила, которая препятствует частицам заполнять все доступное им пространство после применения к ним какой-либо внешней силы. Сходу его расчет весьма затруднителен, однако нашу задачу можно значительно упростить, применив теорему разложения Гельмгольца.

Назовем векторное поле, полученное после расчета перемещения, внешних сил и вязкости. Оно будет иметь ненулевую дивергенцию, что противоречит условию несжимаемости жидкости (), и чтобы это исправить, необходимо рассчитать давление. Согласно теореме разложения Гельмгольца, можно представить как сумму двух полей:

где — и есть искомое нами векторное поле с нулевой дивергенцией. Доказательство этого равенства в данной статье приводиться не будет, однако в конце вы сможете найти ссылку с подробным объяснением. Мы же можем применить оператор набла к обоим частям выражения, чтобы получить следующую формулу для расчета скалярного поля давления:

Записанное выше выражение представляет из себя уравнение Пуассона для давления. Его мы также можем решить вышеупомянутым методом Якоби, и тем самым найти последнюю неизвестную переменную в уравнении Навье-Стокса. В принципе, системы линейных уравнений можно решать самыми разными и изощренными способами, но мы все же остановимся на самом простом из них, чтобы еще больше не нагружать данную статью.

Граничные и начальные условия

Любое дифференциальное уравнение, моделируемое на конечной области, требует правильно заданных начальных или граничных условий, иначе мы с очень большой вероятностью получим физически неверный результат. Граничные условия устанавливаются для контролирования поведения жидкости близ краев координатной сетки, а начальные условия задают параметры, которые имеют частицы в момент запуска программы.

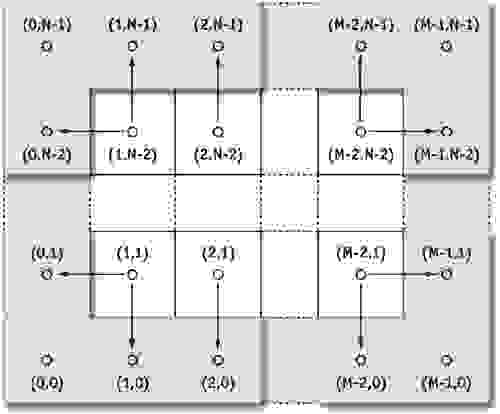
Начальные условия будут весьма простыми — изначально жидкость неподвижна (скорость частиц равна нулю), и давление также равно нулю. Граничные условия будут задаваться для скорости и давления приведенными формулами:

Тем самым, скорость частиц на краях будет противоположна скорости у краев (тем самым они будут отталкиваться от края), а давление равно значению непосредственно рядом с границей. Данные операции следует применить ко всем ограничивающим элементам массива (к примеру, есть размер сетки , то алгоритм мы применим для клеток, отмеченных на рисунке синим):

Краситель

В формуле отвечает за пополнение красителем области (возможно, в зависимости от того, куда нажмет пользователь), непосредственно является количество красителя в точке, а — коэффициент диффузии. Решить его не составляет большого труда, так как вся основная работа по выводу формул уже проведена, и достаточно лишь сделает несколько подстановок. Краску можно реализовать в коде как цвет в формате RGB, и в таком случае задача сводится к операциям с несколькими вещественными величинами.

Завихренность

есть результат применения ротора к вектору скорости (его определение дано в начале статьи), — градиент скалярного поля абсолютных значений . представляет нормализованный вектор , а — константа, контролирующая, насколько большими будут завихренности в нашей жидкости.

Метод Якоби для решения систем линейных уравнений

Для нас — элементы массива, представляющие скалярное или векторное поле. — номер итерации, его мы можем регулировать, чтобы как увеличить точность расчета или наоборот уменьшить, и повысить производительность.

Для расчет вязкости подставляем: , , , здесь параметр — сумма весов. Таким образом, нам необходимо хранить как минимум два векторных поля скоростей, чтобы независимо считать значения одного поля и записывать их в другое. В среднем, для расчета поля скорости методом Якоби необходимо провести 20-50 итераций, что весьма много, если бы мы выполняли вычисления на CPU.

Для уравнения давления мы сделаем следующую подстановку: , , , . В результате мы получим значение в точке. Но так как оно используется только для расчета градиента, вычитаемого из поля скорости, дополнительные преобразования можно не выполнять. Для поля давления лучше всего выполнять 40-80 итераций, потому что при меньших числах расхождение становится заметным.

Реализация алгоритма

Реализовывать алгоритм мы будем на C++, также нам потребуется Cuda Toolkit (как его установить вы можете прочитать на сайте Nvidia), а также SFML. CUDA нам потребуется для распараллеливания алгоритма, а SFML будет использоваться только для создания окна и отображения картинки на экране (В принципе, это вполне можно написать на OpenGL, но разница в производительности будет несущественна, а вот код увеличится еще строк на 200).

Cuda Toolkit

Сначала мы немного поговорим о том, как использовать Cuda Toolkit для распараллеливания задач. Более подробный гайд предоставляется самой Nvidia, поэтому здесь мы ограничимся только самым необходимым. Также предполагается, что вы смогли установить компилятор, и у вас получилось собрать тестовый проект без ошибок.

Чтобы создать функцию, исполняющуюся на GPU, для начала необходимо объявить, сколько ядер мы хотим использовать, и сколько блоков ядер нужно выделить. Для этого Cuda Toolkit предоставляет нам специальную структуру — dim3, по умолчанию устанавливающую все свои значения x, y, z равными 1. Указывая ее как аргумент при вызове функции, мы можем управлять количеством выделяемых ядер. Так как работаем мы с двумерным массивом, то в конструкторе необходимо установить только два поля: x и y:

где size_x и size_y — размер обрабатываемого массива. Сигнатура и вызов функции выглядят следующим образом (тройные угловые скобки обрабатываются компилятором Cuda):

В самой функции можно восстановить индексы двумерного массива через номер блока и номер ядра в этом блоке по следующей формуле:

Следует отметить, что функция, исполняемая на видеокарте, должна быть обязательно помечена тегом __global__ , а также возвращать void, поэтому чаще всего результаты вычислений записываются в передаваемый как аргумент и заранее выделенный в памяти видеокарты массив.

За освобождение и выделение памяти на видеокарте отвечают функции CudaMalloc и CudaFree. Мы можем оперировать указателями на область памяти, которые они возвращают, но получить доступ к данным из основного кода не можем. Самый простой способ вернуть результаты вычислений — воспользоваться cudaMemcpy, схожей со стандартным memcpy, но умеющей копировать данные с видеокарты в основную память и наоборот.

SFML и рендер окна

Вооружившись всеми этими знаниями, мы наконец можем перейти к непосредственному написанию кода. Для начала давайте создадим файл main.cpp и разместим туда весь вспомогательный код для рендера окна:

строка в начале функции main

создает изображение формата RGBA в виде одномерного массива с константной длиной. Его мы будем передавать вместе с другими параметрами (позиция мыши, разница между кадрами) в функцию computeField. Последняя, как и несколько других функций, объявлены в kernel.cu и вызывают код, исполняемый на GPU. Документацию по любой из функций вы можете найти на сайте SFML, в коде файла не происходит ничего сверхинтересного, поэтому мы не будем надолго на нем останавливаться.

Вычисления на GPU

Чтобы начать писать код под gpu, для начала создадим файл kernel.cu и определим в нем несколько вспомогательных классов: Color3f, Vec2, Config, SystemConfig:

Атрибут __host__ перед именем метода означает, что код может исполнятся на CPU, __device__ , наоборот, обязует компилятор собирать код под GPU. В коде объявляются примитивы для работы с двухкомпонентными векторами, цветом, конфиги с параметрами, которые можно менять в рантайме, а также несколько статических указателей на массивы, которые мы будем использовать как буферы для вычислений.

cudaInit и cudaExit также определяеются достаточно тривиально:

В функции инициализации мы выделяем память под двумерные массивы, задаем массив цветов, которые мы будем использовать для раскраски жидкости, а также устанавливаем в конфиг значения по умолчанию. В cudaExit мы просто освобождаем все буферы. Как бы это парадоксально не звучало, для хранения двумерных массивов выгоднее всего использовать одномерные, обращение к которым будет осуществляться таким выражением:

Начнем реализацию непосредственного алгоритма с функции перемещения частиц. В advect передаются поля oldField и newField (то поле, откуда берутся данные и то, куда они записываются), размер массива, а также дельта времени и коэффициент плотности (используется для того, чтобы ускорить растворение красителя в жидкости и сделать среду не сильно чувствительной к действиям пользователя). Функция билинейной интерполяции реализована классическим образом через вычисление промежуточных значений:

Функцию диффузии вязкости было решено разделить на несколько частей: из главного кода вызывается computeDiffusion, которая вызывает diffuse и computeColor заранее указанное число раз, а затем меняет местами массив, откуда мы берем данные, и тот, куда мы их записываем. Это самый простой способ реализовать параллельную обработку данных, но мы расходует в два раза больше памяти.

Обе функции вызывают вариации метода Якоби. В теле jacobiColor и jacobiVelocity сразу же идет проверка, что текущие элементы не находятся на границе — в этом случае мы должны установить их в соответствии с формулами, изложенными в разделе Граничные и начальные условия.

Применение внешней силы реализовано через единственную функцию — applyForce, принимающую как аргументы позицию мыши, цвет красителя, а также радиус действия. С ее помощью мы можем придать скорость частицам, а также красить их. братная экспонента позволяет сделать область не слишком резкой, и при этом достаточно четкой в указанном радиусе.

Расчет завихренности представляет из себя уже более сложный процесс, поэтому его мы реализуем в computeVorticity и applyVorticity, заметим также, что для них необходимо определить два таких векторных оператора, как curl (ротор) и absGradient (градиент абсолютных значений поля). Чтобы задать дополнительные эффекты вихря, мы умножаем компоненту вектора градиента на , а затем нормализируем его, разделив на длину (не забыв при этом проверить, что вектор ненулевой):

Следующим этапом алгоритма будет вычисление скалярного поля давления и его проекция на поле скорости. Для этого нам потребуется реализовать 4 функции: divergency, которая будет считать дивергенцию скорости, jacobiPressure, реализующую метод Якоби для давления, и computePressure c computePressureImpl, проводящие итеративные вычисления поля:

Проекция умещается в две небольшие функции — project и вызываемой ей gradient для давления. Это, можно сказать, последний этап нашего алгоритма симуляции:

После проекции мы смело можем перейти к отрисовке изображения в буфер и различным пост-эффектам. В функции paint выполняется копирование цветов из поля частиц в массив RGBA. Также была реализована функция applyBloom, которая подсвечивает жидкость, когда на нее наведен курсор и нажата клавиша мыши. Из опыта, такой прием делает картину более приятной и интересной для глаз пользователя, но он вовсе не обязателен.

В постобработке также можно подсвечивать места, в которых жидкость имеет наибольшую скорость, менять цвет в зависимости от вектора движения, добавлять различные эффекты и прочее, но в нашем случае мы ограничимся своеобразным минимумом, ведь даже с ним изображения получаются весьма завораживающими (особенно в динамике):

И под конец у нас осталась одна главная функция, которую мы вызываем из main.cpp — computeField. Она сцепляет воедино все кусочки алгоритма, вызывая код на видеокарте, а также копирует данные с gpu на cpu. В ней же находится и расчет вектора импульса и выбор цвета красителя, которые мы передаем в applyForce:

Заключение

В этой статье мы разобрали численный алгоритм решения уравнения Навье-Стокса и написали небольшую программу-симуляцию для несжимаемой жидкости. Быть может мы и не разобрались во всех тонкостях, но я надеюсь, что материал оказался для вас интересным и полезным, и как минимум послужил хорошим введением в область моделирования жидкостей.

Как автор данной статьи, я буду искренне признателен любым комментариям и дополнениям, и постараюсь ответить на все возникшие у вас вопросы под этим постом.

Дополнительный материал

Весь исходный код, приведенный в данной статье, вы можете найти в моем Github-репозитории. Любые предложения по улучшению приветствуются.

Оригинальный материал, послуживший основой для данной статьи, вы можете прочесть на официальном сайте Nvidia (англ). В нем также представлены примеры реализации частей алгоритма на языке шейдеров:
developer.download.nvidia.com/books/HTML/gpugems/gpugems_ch38.html

Доказательство теоремы разложения Гельмгольца и огромное количество дополнительного материала про механику жидкостей можно найти в данной книге (англ, см. раздел 1.2):
Chorin, A.J., and J.E. Marsden. 1993. A Mathematical Introduction to Fluid Mechanics. 3rd ed. Springer.

Канал одного англоязычного ютубера, делающего качественный контент, связанной с математикой, и решением дифференциальных уравнений в частности (англ). Очень наглядные ролики, помогающие понять суть многих вещей в математике и физике:
3Blue1Brown — YouTube
Differential Equations (3Blue1Brown)

Также выражаю благодарность WhiteBlackGoose за помощь в подготовке материала для статьи.

И под конец небольшой бонус — несколько красивых скриншотов, снятых в программе:

Прямой поток (дефолтные настройки)

Водоворот (большой радиус в applyForce)

Волна (высокая завихренность + диффузия)

Также по многочисленным просьбам добавил видео с работой симуляции:

Уравнения гидродинамики

Вы будете перенаправлены на Автор24

Гидродинамика – обширный и важный раздел гидравлики, исследующий основные законы движения идеальной жидкости и ее взаимосвязь с подвижными и неподвижными поверхностями.

Рисунок 1. Уравнение Бернулли. Автор24 — интернет-биржа студенческих работ

Движение физического вещества состоит из достаточно сложного перемещения отдельных атомов молекул. В целях упрощения длительного расчета вводится определение струйчатой модели стабильности. Согласно этой модели, весь поток включает в себя отдельные элементарные струйки, рассмотрение которых в отдельности дает шанс понять закономерности потока жидкости в целом.

С точки зрения математической формулировки движения текучих и постоянных сред, нет разницы между газом и жидкостью. Иногда жидкостью называют несжимаемое пространство, а газом называют среду, у которой начальная плотность существенно меняется со временем.

Жидкость – такое состояние физического пространства, при котором она быстро и легко деформируется под влиянием внутренних и внешних сил.

В отличие от твердого материального тела жидкость не оказывает особое сопротивления сдвиговым нагрузкам, и поэтому такому объему без труда можно придать любую форму. В то же время жидкость может самостоятельно сопротивляться нормальным напряжениям сжатия или растяжения, иногда даже намного сильнее, чем физические вещества. Данная особенность жидкости широко применяется в разнообразных гидравлических машинах и устройствах, например, в гидравлических домкратах и прессах.

Жидкость в основном характеризуется несколькими основными параметрами:

• плотность $ρ$;
• динамическая вязкость $μ$;
• теплоемкость $c$;
• теплопроводность $\lambda$.

Готовые работы на аналогичную тему

В гидродинамике исследуются математические модели течений газа и жидкости в разных условиях. Эти модели в первую очередь представляют собой концепции дифференциальных уравнений при частных и производных обстоятельствах.

Основные уравнения гидродинамики

Главными гидродинамическими уравнениями являются уравнение неразрывности или сплочённости сред, а также уравнение Бернулли.

Уравнение неразрывности представляет собой формулу стабильности расхода и записывается следующим образом:

$dQ_1 + dQ_2 = dQ = const$, где:

$Q_1, Q_2, Q$ – скорости начального движения частиц жидкости в различных живых сечениях струйки.

Для потока уравнение сплоченности сред будет выглядеть так:

Уравнение Бернулли считается фундаментальным законом гидродинамики. Оно устанавливает взаимосвязь между скоростью, давлением, и положение исследуемого элемента в пространстве. Посредством этого уравнения решается огромный круг сложных инженерных задач.

Для упрощения изучения общих и важных закономерностей, присущих постоянно движущейся жидкости, ее часто представляют в виде неизменной среды, не обладающей внутренней энергией и трением. Такую жидкость в физике называют идеальной.

Уравнение Бернулли для элементарной струйки идеальной жидкости чаще всего используется при расчетах и имеет следующий вид

• $Z$ – геометрический стабильный напор, или потенциальная удельная энергия начального положения;
• $\frac

  $ — изометрический напор, или удельная сила давления;

• $\frac<2>^<2><2g>$ — cкоростной напор, или кинетическая энергия.

Это уравнение также считается формулой закона сохранения и удержания энергии для движущейся жидкости. В этом заключается ее основной физический смысл.

При длительном движении реальной жидкости, обладающей определенной вязкостью, часть ее внутренней энергии автоматически затрачивается на преодоление сил трения. Этот показатель в виде тепла рассеивается в окружающую среду. Такое явление необратимо и в науке называется диссипацией. Диссипируемую величину в гидродинамике называют гидравлическими потерями.

Уравнения Навье-Стокса для несжимаемой жидкости

Рисунок 2. Уравнение Навье-Стокса. Автор24 — интернет-биржа студенческих работ

Плотность несжимаемой жидкости в любых ситуациях постоянна, в математической модели она выступает как изначальный заданный параметр. Уравнение неразрывности при этом имеет такой вид

Система уравнений всегда замкнута, так как содержит 4 формулы для трёх компонент скорости и давления.

В развернутой форме для компонент скоростного вектора $v = G$ в декартовой системе координат $ x, y, z$ уравнения Навье-Стокса для несжимаемой жидкости с постоянной вязкостью записывается так:

Взгляд на температуру как основную меру внутренней энергии, непосредственно связанную со скоростью движения атомов и молекул, используется в физике, а в гидродинамике был принят феноменологический метод, при котором исследуют макроскопические характеристики переноса тепла. В частности, вводится определение теплового потока между нагретыми частями сплошного пространства.

Тепловой поток $Q$ – это точное количество тепла, которое трансформируется в единицу времени $Q = \frac<Дж><сВт>$.

Плотность теплового постоянного потока $q = \frac$ – это протекающий через единицу площади поток.

Тепло в гидродинамике переносится разными механизмами:

1. Молекулярная термодиффузия или теплопроводность. В горячей части определенной среды молекулы более подвижны, они возбуждают своим действием соседние, в результате чего повышается температура.
2. Конвекция. Данный процесс вызван движением жидкости. Поток жидкости непосредственно переносит начальную температуру из одной части пространства в другую. Если среда нагрета равномерно, конвективного теплового поток не будет даже при наличии движения.
3. Излучение. Это передача внутреннего тепла в виде электромагнитных волн. Например, тепло от раскаленной печки или солнечная энергия.

Закон Паскаля

В случае, когда все массовые силы отсутствуют, т.е. $g = 0$, из этих формул получается, что $p = 0$. откуда следует, что $p = const$. Это решение носит в науке название закона Паскаля, который предполагает, что в покоящейся жидкости (газе) при отсутствии массовых и постоянных сил давление постоянно.

Уравнение состояния идеального газа $p = ρRT$ , отсюда можно найти плотность газа в зависимости от начальной температуры

Это обыкновенное дифференциальное уравнение первого порядка для внутреннего давления $p = z $. Оно решается согласно принципу разделения переменных:

Закон Паскаля в гидродинамике даёт формулу изменения давления с высотой, если известно точное распределение температуры по заданной величине. В частном случае, это действует в случае, если считать атмосферу изотермической, когда $Т = const$.

Эта формула доказывает, что давление в изотермической атмосфере постепенно убывает с высотой по экспоненциальному закону.

ГИДРОАЭРОМЕХАНИКА

ГИДРОАЭРОМЕХАНИКА – наука о движении и равновесии жидкостей и газов. При планировании физических экспериментов или при их проведении необходимо создавать теоретические модели, которые либо предсказывают возможные результаты этих экспериментов, либо объясняют уже полученные. Только в тесном взаимодействии теории и эксперимента можно понять то, что происходит в окружающем нас физическом мире. Для создания той или иной количественной или качественной модели физического явления необходим математический фундамент, на основе которого строятся такие модели. Под математическим фундаментом в данном случае подразумеваются те дифференциальные уравнения и те граничные и начальные условия, с помощью которых можно было бы описывать рассматриваемое физическое явление. Гидромеханика и предлагает модели и аппарат для иcследования явлений, происходящих в жидкостях и газах.

О гипотезе сплошности среды.

Гидроаэромеханика изучает движения жидкостей и газов в приближении, когда они могут рассматриваться как сплошные среды, т.е. среды, непрерывным образом заполняющие рассматриваемое пространство течения. Чтобы решать математические проблемы, связанные с расчетом движения различных объектов (самолетов, ракет, кораблей и др.) в воздухе или воде, с изучением волновых процессов в жидкостях и газах, с их течениями по трубам и каналам и т.п., необходим математический аппарат, описывающий эти явления. Этим аппаратом и являются уравнения гидроаэромеханики, которые опираются на гипотезу сплошности среды, т.е. на гипотезу о том, что частицы жидкости или газа непрерывным образом заполняют занимаемую ими часть физического пространства.

Возникает естественный вопрос: при каких предположениях справедлива эта гипотеза? Если для жидкостей (воды, жидких металлов и т.п.) эта гипотеза более или менее очевидна, то для достаточно разреженных газов (например, занимающих космическое пространство, включая атмосферы звезд, планет и Солнца), которые состоят из отдельных атомов или молекул, а также других физических объектов, к которым применим аппарат гидроаэромеханики, она требует своего обоснования. Так, например, при расчете торможения искусственных спутников Земли использование математического аппарата гидроаэромеханики не представляется возможным, в то время как именно этот аппарат используется при расчете торможения космических объектов, входящих в плотные слои атмосфер Земли и планет (например, метеоритов или возвращаемых на Землю космических кораблей и пр.). На этот вопрос легко ответить при выводе уравнений. Однако из этого вывода следует, что гипотеза сплошности среды справедлива, в частности, в том случае, когда характерный размер обтекаемого тела L (например, радиус сферического спутника) много больше длины свободного пробега атомов или молекул газа l, т.е. длины между последовательными их столкновениями.

Замкнутая система уравнений гидроаэромеханики.

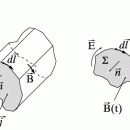
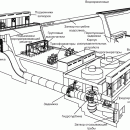
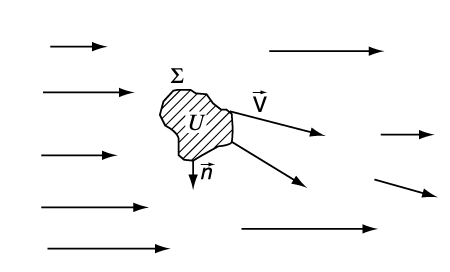
Уравнения гидроаэромеханики в их упрощенном виде представляют собой сложную систему нелинейных дифференциальных уравнений для массовой плотности r (масса жидкости или газа в единице объема), вектора скорости V и давления p, которые, в свою очередь, являются функциями пространственных координат (например, x, y и z в декартовой системе координат) и времени t. Не вдаваясь в математические подробности вывода этих уравнений, можно рассмотреть основные идеи этого вывода, тем более, что эти уравнения представляют собой известные даже из школьных учебников законы сохранения массы, импульса и энергии. Для этого рассматривается некоторый физический объем, непрерывным образом заполненный жидкостью или газом. На рис. 1 изображена движущаяся жидкость (или газ), непрерывным образом заполняющая некоторую часть физического пространства. Выделим из нее некоторый объем U (ограниченный поверхностью S), который в течение всего времени движения состоит из одних и тех же частиц жидкости (этот объем заштрихован).

Очевидно, что при своем движении масса жидкости, заключенная в объеме U, остается постоянной (если, конечно, нет каких-либо дополнительных источников этой массы), хотя сам объем может сильно деформироваться, поскольку частицы не скреплены жестко, как в твердом теле. Если выделить из рассматриваемого объема бесконечно малый элемент DU, то очевидно, что в этом элементе масса жидкости или газа будет равна rDU. Тогда закон сохранения массы, заключенной в выделенном объеме U, можно записать в виде

т.е. масса жидкости или газа, заключенная в выделенном объеме U, не изменяется со временем. Здесь интеграл берется по выделенному объему U, который меняется со временем t. Если использовать формулу производной по времени от интеграла по движущемуся объему, можно получить уравнение

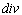
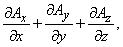
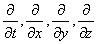
где оператор дивиргенции , примененный к произвольному вектору А, в декартовой системе координат будет имеет вид

а – частные производные по времени t и координатам x, y, z соответственно.

Закон сохранения массы в интегральной форме справедлив как для непрерывных, так и для разрывных функций r и V. Для непрерывных функций закон сохранения массы можно записать в дифференциальной форме

Это уравнение в гидроаэромеханике обычно называется уравнением неразрывности.

Аналогично можно записать теперь закон сохранения импульса. Импульс единицы объема жидкости, равен rV, в элементарном объеме rDU, а в выделенном объеме U –

Обобщение второго закона Ньютона на жидкие среды заключается в том, что кроме массовых сил (например, силы гравитации), которые действуют на любую частицу жидкости, находящуюся внутри выделенного объема U, действуют еще поверхностные силы, которые возникают от воздействия частиц жидкости, примыкающих к поверхности S с внешней от выделенного объема U стороне. Тогда закон сохранения импульса имеет вид

где p_n– вектор поверхностной силы, который действует на элемент поверхности S с единичным вектором нормали n. Одной из основных проблем гидроаэромеханики, окончательно решенной в середине 19 в., является явное определение поверхностных сил. В рамках используемого здесь так называемого феноменологического подхода к получению уравнений гидроаэромеханики, поверхностные силы определяются эмпирически. Дифференцируя по времени интеграл слева в уравнении импульса, как это делалось при выводе уравнения неразрывности, и переходя от поверхностного интеграла справа к объемному, можно написать дифференциальные уравнения движения для непрерывных функций в виде

.

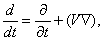
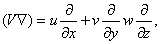
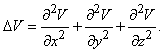
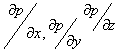
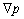
а величины u, v и w, а также – являются проекциями векторов скорости V и градиента давления на оси Ox, Oy и Oz соответственно.

Это уравнение, называемое уравнением Навье – Стокса, выписано в наиболее простой форме для несжимаемой жидкости, где поверхностные силы сводятся к нормальному давлению р, а последний член справа представляет собой «вязкие» силы (m – коэффициент вязкости) в предположении, что r = const.

Впервые уравнение движения было выведено в середине 18 в. Л.Эйлером, когда он работал в Петербургской Академии наук. Поскольку эффекты вязкости в жидкости в то время еще не были известны, то Эйлер получил это уравнение при m = 0. В честь его эти уравнения были названы уравнениями Эйлера. Только в 1822 французским инженером Навье в уравнения Эйлера были введены силы, связанные с вязкостью, определяемой коэффициентом m. В общей форме, справедливой и для сжимаемого газа, уравнение получено Стоксом и получило название уравнения Навье – Стокса.

Для несжимаемой жидкости дифференциальные уравнения неразрывности и импульса (одно скалярное и одно векторное) являются замкнутой системой уравнений для определения вектора скорости V и скалярного давления р (r = const). Если же r № const, то требуется дополнительное уравнение. Это уравнение получается из закона сохранения энергии.

Обобщение закона сохранения энергии на случай движения жидкостей и газов получается аналогично обобщению второго закона Ньютона, однако, в силу наличия теплового движения в жидкостях и газах, энергия, приходящаяся на единицу объема, состоит из кинетической энергии rV 2 /2 и внутренней энергией re, связанной с тепловым движением частиц газа или жидкости. Полная энергия в элементе объема DU равна r(V 2 /2 + e)DU.

Изменение полной энергии в выделенном объеме U равно притоку тепла через поверхность S за счет теплопроводности, а также работе массовых и поверхностных сил, т.е. вместо закона сохранения импульса, получается уравнение

где n – единичный вектор нормали к поверхности S.

Для совершенного газа e = c_v T, где с_v – теплоемкость при постоянном объеме, T – температура, а для вектора потока тепла обычно принимается эмпирический закон Фурье q = – l 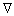T (l – коэффициент теплопроводности). После соответствующего дифференцирования по времени левой части уравнения энергии, перехода от поверхностных интегралов к объемным и при использовании уравнения неразрывности и уравнения движения, можно получить так называемое уравнение притока тепла для непрерывных функций

Все эти уравнения, вместе с уравнением состояния для совершенного газа

где R = (с_р – с_v ) – газовая постоянная, а с_р – теплоемкость при постоянном давлении, и законом Фурье

Образуют замкнутую систему уравнений гидроаэромеханики для определения вектора скорости V, давления p, плотности r и температуры Т.

Если какое либо физическое явление мало зависит от диссипативных процессов (вязкости и теплопроводности), то уравнения эти уравнения сводятся к уравнениям гидроаэромеханики идеальной жидкости. В этом случае замкнутой системой уравнений для определения р, r, V и Т является система

Последнее уравнение есть адиабатический закон, который легко сводится к закону сохранения энтропии. Здесь g = с_p/c_v – показатель адиабаты, т.е. отношение теплоемкости при постоянном давлении к теплоемкости при постоянном объеме.

Гидростатика

представляет собой частный случай гидроаэромеханики, который изучает равновесие жидкостей и газов, т.е. их состояние при отсутствии гидродинамической скорости (V = 0). Результаты и методы гидростатики имеют большое значение для многих задач, важных как с практической, так и с общенаучной точек зрения. В гидростатике рассматриваются задачи, связанные с равновесием воды в водных бассейнах, воздуха в атмосфере Земли, решаются задачи расчета сил, которые действуют на тела, погруженные в жидкость или газ, определяются распределения давления, плотности, температуры в атмосферах планет, звезд, Солнца и множество других задач.

Уравнения гидростатики получаются из уравнений гидроаэромеханики при V = 0. В частности, уравнения сохранения импульса дает

Откуда, в частности, следует известный еще из школьных учебников закон Паскаля, согласно которому при отсутствии внешних массовых сил (F = 0) давление всюду является постоянным (p = const ).

Равновесие совершенного газа в поле сил тяжести.

Пусть есть газ в центральном поле сил тяжести. Уравнения равновесия в сферической системе координат будут в этом случае записываются как:

Здесь r, q и c – соответственно расстояние до притягивающего центра массы М, помещенного в начало координат, угол, отсчитываемый от полярной оси Оz, и угол в плоскости Оxy, G – гравитационная постоянная, равная 6,67Ч10 –8 дин см 2 г –2 .

Из этих уравнений видно, что в центрально-симметричном поле гравитации давление зависит только от расстояния до этого центра (легко показать, что давление не зависит и от времени). Легко также показать, что плотность и температура также зависят только от координаты r. Интегрирование первого из этих уравнений приводит к так называемой барометрической формуле, если под М понимать массу Земли, планеты, звезды, Солнца и др. При использовании уравнения состояния барометрическая формула имеет вид

где p₀ – давление на некотором расстоянии r = r₀ от притягивающего центра (для Земли, например, это может быть давление на уровне моря). Эта формула определяет распределение давления в атмосферах звезд, Земли, планет, Солнца и др., если известно распределение температуры Т(r), однако эту температуру часто нельзя определить из написанного ранее уравнения притока тепла, так как в нем учитывается только приток тепла за счет теплопроводности, в то время как для перечисленных атмосфер есть другие источники тепла, неучтенные в приведенном уравнении. Например, атмосфера Солнца разогревается различного рода волновыми процессами, а атмосфера Земли перерабатывает энергию солнечного излучения и т.п., поэтому для определения распределения давления в атмосферах небесных тел при помощи барометрической формулы часто используются эмпирические зависимости Т(r).

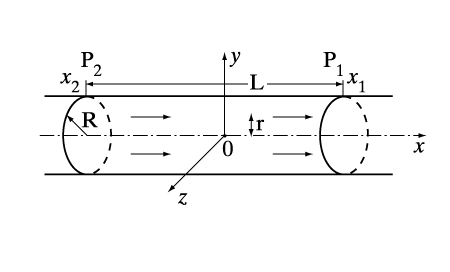
Можно, например, рассчитать распределения давления в атмосфере Земли до расстояний в 11 км от ее поверхности. Если выбрать декартову систему координат с началом на поверхности Земли и направить ось Oz вертикально вверх, тогда в барометрической формуле вместо координаты r нужно брать координату z = r – R_Е, где R_Е – радиус Земли. Поскольку этот радиус много больше толщины атмосферы (z p₁), не влияют на течение в большей части этой трубы, то легко получить точное аналитическое решение уравнения Навье – Стокса в виде

где u – скорость жидкости вдоль оси х, совпадающей с осью симметрии трубы, а r – расстояние от этой оси. Из этой видно, что профиль скорости в трубе является параболическим. На стенках трубы скорость обращается в нуль вследствие прилипания жидкости из-за эффекта вязкости. Такое течение было изучено в середине 19 в. Пуазейлем и Гагеном на примере течений жидкостей в капиллярах и получило название течения Гагена – Пуазейля.

Очевидно, при постоянном потоке (не зависящем от r) жидкости у входа в трубу и на ее начальном участке профиль скорости не будет совпадать с приведенным решением. Параболический профиль устанавливается лишь на достаточно большом расстоянии от входного участка, именно поэтому для получения решения нужно предположить, что труба достаточно длинная, при этом для таких труб это точное решение хорошо совпадает с экспериментальными данными.

Полученное решение описывает стационарное, гладко-слоистое течение, которое обычно называют ламинарным. Однако из практики известно, что в трубах иногда течение бывает нестационарным, с пульсациями скорости, с перемешиванием между слоями, это течение обычно называется турбулентным. Опыты Рейнольдса, проведенные в 1883, показали, что при достаточно больших значениях числа r U L/m, где U – средняя по сечению трубы скорость жидкости, параболический профиль становится неустойчивым по отношению к малым возмущениям, а при дальнейшем увеличении этого числа течение в трубе становится турбулентным. Это число получило название числа Рейнольдса (Re), которое играет очень важную роль в различных задачах гидроаэромеханики. В частности оно характеризует отношение инерционных сил (левая часть уравнения) к силам вязкости, при этом часто силами вязкости можно пренебречь и использовать уравнения гидроаэромеханики идеальной жидкоститолько при Re >> 1.

Течения идеальных жидкостей и газов.

Часто важные в приложениях задачи рассматривают на основе уравнений гидроаэромеханики идеальной жидкости, а не на полных уравнениях. Это связано с тем, что математически уравнения идеальной гидроаэромеханики существенно проще. Если нужно определить подъемную силу крыла самолета при малых дозвуковых скоростях, то вязкие силы пренебрежимо малы и нет необходимости использовать уравнения Навье – Стокса. Однако для определения сопротивления такого крыла при движении его в воздухе вязкие силы оказываются определяющими и необходимо использовать более сложный математический аппарат, связанный с уравнениями Навье – Стокса.

Интеграл Бернулли.

При некоторых предположениях уравнения гидромеханики идеальной жидкости можно один раз проинтегрировать, они имеют решения, одним из которых является интеграл Бернулли для стационарных течений (по имени современника Эйлера математика Бернулли, впервые получившего этот интеграл)

где P (p) = т dp/r(p) – функция давления, U – потенциал внешних массовых сил, С – постоянная вдоль линии тока l (линия тока совпадает с вектором скорости течения V). Так, например, для несжимаемой жидкости в поле земного тяготения это уравнение имеет вид

Для адиабатических течений интеграл Бернулли в отсутствии внешних массовых сил имеет вид

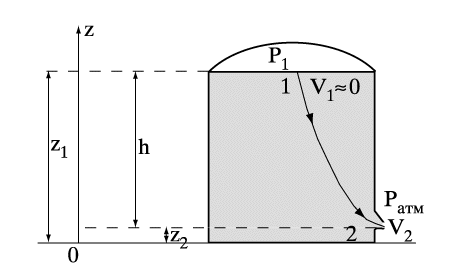
В качестве примера использования интеграла Бернулли можно определить скорость истечения несжимаемой жидкости из сосуда (рис. 5). При истечении жидкости из этого сосуда уровень жидкости понижается, т.е. скорость поверхности жидкости, вообще говоря, отлична от нуля. Однако при достаточно широком сосуде с узким отверстием вытекания можно принять, что V₁ » 0. Поскольку по всей поверхности жидкости в сосуде давление р₁ = const, то постоянная вдоль линии тока на всех линиях тока будет одинаковой. Интеграл Бернулли вдоль какой-нибудь линии тока, например, соединяющей точки 1 (на поверхности) и 2 (у выходного отверстия)

где р_атм – атмосферное давление у выходного отверстия. Отсюда легко получить формулу для скорости истечения V₂. В частном случае р_атм = р₁ получаем так называемую формулу Торичелли для истечения жидкости из широкого сосуда с узким выходным отверстием

по имени итальянского ученого Э.Торричелли (1608–1647). Здесь h = (z₁ – z₂ ). Для ванны с высотой налитой воды примерно 0,5 м скорость истечения V₂ » 3,1м/сек.

Уравнения движения идеальной жидкости имеют еще один интеграл для нестационарных течений, который называется интегралом Коши – Лагранжа. Он справедлив для течений, в которых отсутствуют вихри. Его часто, например, используют при рассмотрении волновых движений жидкости или газа.

Ударные волны как одно из важных проявлений сжимаемости газа.

Математически уравнения идеальной гидроаэромеханики допускают разрывные решения, т.е. решения, которые имеют скачки параметров газа (плотности, давления, скорости и температуры). Одним из таких проявлений в природе является образование ударной волны около летящего со сверхзвуковой скоростью тела в плотных слоях атмосферы Земли. Например, образование ударной волны около летающих сверхзвуковых самолетов или ударных волн около метеоритов, вторгающихся в плотные слои атмосферы Земли с большими сверхзвуковыми скоростями. В условиях космического пространства хорошо известны межпланетные ударные волны, которые чаще всего являются результатом активных процессов на Солнце (например, вспышек).

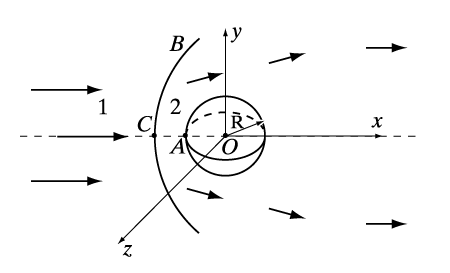
Известно, что около пассажирских самолетов, летающих главным образом с большими дозвуковыми, никакие ударные волны не образуются. Пусть есть сферическое тело радиуса R (рис. 6), которое летит в воздухе со сверхзвуковой скоростью. Тогда впереди такого тела образуется ударная волна В, являющаяся границей между областями 1 и 2, которые отличаются значениями параметров газа. В системе координат, связанной с летящим телом. поток газа набегает на покоящееся тело. Пусть ось Оx направлена вдоль скорости потока, а V₁, p₁, r1 и T₁ – скорость, давление, плотность и температура, соответственно, в невозмущенном телом потоке газа (до ударной волны). В область 1 возмущения от тела не попадают, поскольку тело движется со сверхзвуковой скоростью. Так как скорость газа в лобовой точке тела А обращается в нуль, то от точки А до точки С на ударной волне есть область дозвуковой скорости газа, которой достигают возмущения воздуха от летящего тела. Физический смысл образования ударной волны и заключается в разделении невозмущенного и возмущенного потоков газа. Если через V₂, p₂, r2 и T₂ обозначить скорость, давление, плотность и температуру газа соответственно сразу же после ударной волны В, то справедливы неравенства

Это означает, что скорость за ударной волной уменьшается, а давление, плотность и температура возрастают. Сильным возрастанием температуры за ударной волной и объясняется оплавление возвращающихся на Землю космических аппаратов и метеоритов, вторгающихся в атмосферу с большими сверхзвуковыми скоростями. Такие ударные волны называются ударными волнами сжатия (плотность газа возрастает). Интересно, что в природе никогда не наблюдались ударные волны разрежения, в которых плотность падает. Математически образование ударных волн разрежения запрещается известной в гидроаэромеханике теоремой Цемплена

Соотношения между параметрами с индексами «1» и «2» можно получить из интегральных законов сохранения массы, импульса и энергии, поскольку они справедливы и для разрывных функций. Такие соотношения называются соотношениями Гюгонио и имеют вид (в системе координат, связанной с ударной волной)

Вместе с уравнением состояния эти соотношения позволяют определить значения параметров газа за ударной волной (индекс «2») по значениям параметров невозмущенного ударной волной потока газа (индекс «1»).

Описанный математический аппарат гидроаэромеханики используется во многих областях естественных наук, при этом для корректности использования этого аппарата требуется только выполнение критерия сплошности среды, т.е. для газов, например, длина свободного пробега частиц должна быть много меньше характерных размеров рассматриваемых объектов обтекания. В частности, в условиях космического пространства часто среда очень разрежена. В таких средах, конечно же, длина свободного пробега частиц очень велика, но размеры самих объектов исследования оказываются во многих случаях существенно больше, т.е. методы гидроаэромеханики применимы и к таким объектам.

В биомеханике при помощи методов гидромеханики исследуются интересные особенности течений биологических жидкостей по сосудам, а в гидрогеологии исследуются, например, задачи динамики внутренних слоев Земли. Все это свидетельствует о важности науки, которая называется «гидроаэромеханика».

Ландау Л.Д. и Лифшиц Е.М. Механика сплошных сред. М., ГИТТЛ, 1954
Чепмен С. и Каулинг Т. Математическая теория неоднородных газов. ИИЛ, М., 1960
Кочин Н.Е., Кибель и Розе. Теоретическая гидромеханика, т.1. Физматгиз, 1963
Кочин Н.Е., Кибель и Розе, Теоретическая гидромеханика, т.2, Физматгиз, 1963
Седов Л.И. Механика сплошной среды. М., Наука, т. 1, 1973
Седов Л.И. Механика сплошной среды. М., Наука, т. 2, 1973
Баранов В.Б. и Краснобаев К.В., Гидродинамическая теория космической плазмы, М., Изд. «Наука», 1977
Эйлер Л. Общие законы движения жидкостей. Известия РАН, сер. МЖГ, 1999, № 6