Система уравнений эйлера в цилиндрических координатах

Уравнение движения в форме Эйлера

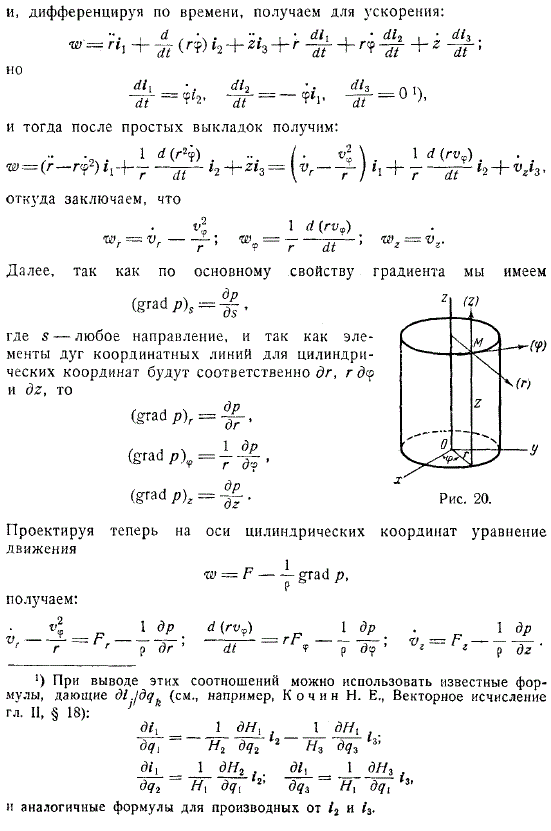
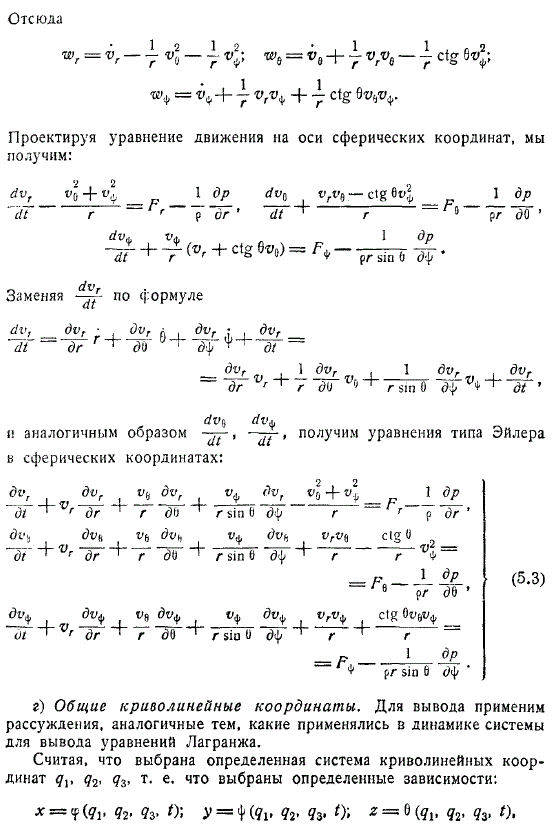
Уравнения движения и формула Эйлера

Уравнения движения Эйлера в виде декартовых координат. Уравнения Эйлера представляют собой проекции ускорения в переменной Эйлера в соответствии с этим разделом гидромеханики уравнения движения и решают уравнение так называемого уравнения гидродинамики Эйлера. Возвращает цилиндрические координаты. Проекция скорости точки на ось цилиндрических координат.

На что указывает кинематика точек.Отложив 3 единичных вектора вдоль оси цилиндрических координат, можно выразить вектор скорости точки в виде, и дифференцируя его во времени вы получите ускорение.

После простого вычисления вы получите кроме того, за счет основных свойств склона, где расположено любое направление, так как имеются, соответственно, элементы общего уравнения движения идеальной жидкости дуги координатной линии цилиндрических координат. Далее строятся уравнения движения по оси цилиндрических координат.

При выводе этих соотношений можно использовать известные формулы, такие как векторные вычисления и аналогичные формулы для производных названий этих уравнений, а также полные производные таким же образом мы достигаем типа дифференциальных уравнений Эйлера их подразделяют на:

• Сферические координаты
• Проекция скорости точки на ось сферы

Поместите вдоль оси сферические координаты единичных вектора
Представляют вектор скорости в некоторой точке в виде
Поэтому, для ускорения, вы получите следующее. Вы можете построить уравнения движения по оси сферы. Отсюда заменяйте формулу аналогично получаем уравнение Эйлера
в сферических координатах.

Общие криволинейные координаты;в заключение мы выводим уравнение Лагранжа, применяя выводы, аналогичные тем, которые используются в динамике системы. Предполагая, что выбрана определенная система криволинейных координат, выбирается определенная зависимость.

Построение уравнения движения

С другой стороны, при построении уравнения движения по оси сферических координат оно выглядит. Отсюда не заменяйте формулу аналогично получаем уравнение Эйлера в сферических координатах.

Общие криволинейные координаты;в заключение мы выводим уравнение Лагранжа, применяя выводы, аналогичные тем, которые используются в динамике системы.

Предполагая, что выбрана определенная криволинейная система координат, выбирается определенная зависимость. Сделать преобразование и когда применяется разбить на дроби.

Полные производные

То же самое верно и для других 2 терминов.Введение в нотацию рабочая сила на единицу массы жидкости и для обобщенных массовых сил найти уравнение движения и векторные формы уравнений движения в криволинейных координатах. Если есть потенциал в массовой силе, то очевидно и уравнения движения. Уравнения формы справедливы для криволинейных координат не только ортогональных.

Проекция скорости на ось криволинейных координат представлена следующей формулой где же хромой фактор выглядит отрицательно.

В случае декартовой ортогональности биологические силы принимают вид положительных поэтому решение получается верным.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Цилиндрическая система координат (цилиндрические координаты)

Для введения цилиндрической системы координат в пространстве выбирается плоскость ( основная плоскость ) и на ней задается полярная система координат с полюсом и полярной осью . Через точку перпендикулярно основной плоскости проведем ось ( ось аппликат ) и выберем ее направление так, чтобы возрастание полярного угла, наблюдаемое со стороны положительного направления оси , происходило против часовой стрелки (рис.2.34,а).

В цилиндрической системе координат положение точки , не принадлежащей оси аппликат, характеризуется полярными координатами точки — ортогональной проекции точки на основную плоскость, и аппликатой — координатой точки — ортогональной проекции точки на ось аппликат. Таким образом, цилиндрические координаты точки — это упорядоченная тройка чисел — полярный радиус , полярный угол и аппликата . У точек, принадлежащих оси аппликат, не определен полярный угол, они задаются указанием нулевого полярного радиуса и аппликатой.

Переход от цилиндрических координат к декартовым (прямоугольным)

С цилиндрической системой координат можно связать прямоугольную систему координат (рис.2.34,б), у которой начало и базисные векторы совпадают с началом цилиндрической системы координат и единичными векторами на полярной оси и оси аппликат соответственно, а базисный вектор выбирается так, чтобы тройка была правой (при этом базис оказывается стандартным).

Наоборот, если в пространстве задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим цилиндрическую систему координат ( связанную с данной прямоугольной ).

Поскольку аппликата точки в прямоугольной системе координат и аппликата в цилиндрической системе координат совпадают, то формулы, связывающие между собой прямоугольные координаты точки и ее цилиндрические координаты , имеют вид, следующий из

Эти формулы перехода позволяют найти прямоугольные координаты по известным цилиндрическим. Обратный переход выполняется по формулам

Главное значение полярного угла находится по формулам (см. рис.2.29).

Пример 2.12. В цилиндрической системе координат :

а) построить координатные поверхности ;

б) найти цилиндрические координаты точки , если известны ее прямоугольные координаты ;

в) найти прямоугольные координаты точки , если известны ее цилиндрические координаты: .

Решение. а) Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении полярного радиуса , является прямой круговой цилиндр, ось которого параллельна оси аппликат (рис.2.35). Этим объясняется название цилиндрической системы координат. Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении полярного угла , является полуплоскость, ограниченная осью аппликат (на рис.2.35 изображены полуплоскости и ). Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении аппликаты , является плоскость, перпендикулярная оси аппликат (на рис.2.35 изображены плоскости и ).

б) Найдем цилиндрические координаты точки . Аппликата , полярный радиус и полярный угол находим по формулам (2.20) (см. пример 2.11):

так как и ортогональная проекция точки на координатную плоскость (основную плоскость) лежит в IV четверти.

в) Найдем прямоугольные координаты точки . По формулам (2.19) вычисляем (см. пример 2.10):

Цилиндрические координаты: система, изменение и упражнения

Цилиндрические координаты: система, изменение и упражнения — Наука

Содержание:

В цилиндрические координаты Они используются для определения местоположения точек в трехмерном пространстве и состоят из радиальной координаты ρ, азимутальной координаты φ и координаты высоты. z.

Точка п расположенная в пространстве проецируется ортогонально на плоскость XY приводя к сути П ‘ в этом самолете. Расстояние от начала координат до точки П ‘ определяет координату ρ, а угол, образованный осью Икс с лучом OP ‘ определяет координату φ. Наконец, координата z ортогональная проекция точки п на оси Z. (см. рисунок 1).

Радиальная координата ρ всегда положительна, азимутальная координата φ изменяется от нуля радиан до двух пи радиан, а координата z может принимать любое действительное значение:

База вектора в цилиндрических координатах

База цилиндрических единичных векторов определяется Uρ, Uφ, Уз.

Вектор Uρ касается прямой φ = ctte и z = ctte (направленной радиально наружу), вектор Uφ касается прямой ρ = ctte, z = ctte и, наконец, Уз имеет то же направление оси Z.

В основании цилиндрического блока вектор положения р точки P записывается векторно так:

р = ρ Uρ + 0 Uφ + z Уз

С другой стороны, бесконечно малое смещение dр из точки P это выражается следующим образом:

dр = dρ Uρ + ρ dφ Uφ + дз Уз

Точно так же бесконечно малый элемент объема dV в цилиндрических координатах равен:

Примеры

Существует бесчисленное множество примеров использования и применения цилиндрических координат. В картографии, например, цилиндрическая проекция, исходя именно из этих координат. Еще примеры:

Пример 1

Цилиндрические координаты находят применение в технике. В качестве примера у нас есть система размещения данных на жестком диске CHS (Cylinder-Head-Sector), которая фактически состоит из нескольких дисков:

— Цилиндр или дорожка соответствует координате ρ.

— Сектор соответствует положению φ диска, вращающегося на высокой угловая скорость.

— Головка соответствует положению z считывающей головки на соответствующем диске.

Каждый байт информации имеет точный адрес в цилиндрических координатах (C, S, H).

Пример 2

Строительные краны фиксируют положение груза в цилиндрических координатах. Горизонтальное положение определяется расстоянием до оси или стрелкой крана ρ и его угловым положением φ относительно некоторой исходной оси. Вертикальное положение груза определяется координатой z высоты.

Решенные упражнения

Упражнение 1

Есть точки P1 с цилиндрическими координатами (3, 120º, -4) и точка P2 с цилиндрическими координатами (2, 90º, 5). Найди Евклидово расстояние между этими двумя точками.

Решение: Прежде всего, мы переходим к нахождению декартовых координат каждой точки по формуле, приведенной выше.

P1 = (3 * cos 120º, 3 * sin 120º, -4) = (-1,5, 2,60, -4)

P2 = (2 * cos 90º, 2 * sin 90º, 5) = (0, 2, 5)

Евклидово расстояние между точками P1 и P2 равно:

d (P1, P2) = √ ((0 — (-1,5)) 2 +(2 – 2.60) 2 +(5 -(-4)) 2 ) =…

Упражнение 2.

Точка P имеет декартовы координаты (-3, 4, 2). Найдите соответствующие цилиндрические координаты.

Решение: Переходим к нахождению цилиндрических координат, используя приведенные выше соотношения:

ρ = √ (x 2 + и 2 ) = √((-3) 2 + 4 2 ) = √(9 + 16) = √(25) = 5

φ = arctan (y / x) = arctan (4 / (- 3)) = -53,13º + 180º = 126,87º

Следует помнить, что функция арктангенса является многозначной с периодичностью 180º. Кроме того, угол φ должен принадлежать второму квадранту, поскольку координаты x и y точки P находятся в этом квадранте. Это причина, по которой к результату φ было добавлено 180 °.

Упражнение 3.

Выразите в цилиндрических координатах и ​​декартовых координатах поверхность цилиндра радиуса 2, ось которого совпадает с осью Z.

Решение: Подразумевается, что цилиндр имеет бесконечную протяженность в направлении z, поэтому уравнение указанной поверхности в цилиндрических координатах имеет вид:

Чтобы получить декартово уравнение цилиндрической поверхности, берется квадрат обоих членов предыдущего уравнения:

Умножаем на 1 оба члена предыдущего равенства и применяем фундаментальное тригонометрическое тождество (сен 2 (φ) + cos 2 (φ) =1 ):

(сен 2 (φ) + cos 2 (φ) ) * ρ 2 = 1 * 4

Скобка предназначена для получения:

(ρ sin (φ)) 2 + (ρ cos (φ)) 2 = 4

Мы помним, что первые круглые скобки (ρ sin (φ)) — это координата y точки в полярных координатах, а круглые скобки (ρ cos (φ)) представляют координату x, поэтому мы имеем уравнение цилиндра в декартовых координатах:

Вышеупомянутое уравнение не следует путать с уравнением окружности в плоскости XY, так как в этом случае оно будет выглядеть так: .

Упражнение 4.

Цилиндр с радиусом R = 1 м и высотой H = 1 м имеет свою массу, распределенную радиально в соответствии со следующим уравнением: D (ρ) = C (1 — ρ / R), где C — постоянная величина C = 1 кг / м. 3 . Найдите общую массу цилиндра в килограммах.

Решение: Во-первых, необходимо понять, что функция D (ρ) представляет объемную массовую плотность и что массовая плотность распределена в цилиндрических оболочках с уменьшающейся плотностью от центра к периферии. Бесконечно малый элемент объема в соответствии с симметрией задачи:

Следовательно, бесконечно малая масса цилиндрической оболочки будет:

Следовательно, общая масса цилиндра будет выражаться следующим образом: определенный интеграл:

M = ∫_или р D (ρ) dV = ∫_или р C (1 — ρ / R) ρ dρ 2π H = 2π H C ∫_или р (1 — ρ / R) ρ dρ

Решение указанного интеграла получить нетрудно, его результат:

∫_или р (1 — ρ / R) ρ dρ = (⅙) R 2

Включая этот результат в выражение массы цилиндра, получаем:

M = 2π H C (⅙) R 2 = ⅓ π H C R 2 =

⅓ π 1м * 1кг / м 3 * 1 м 2 = π / 3 кг ≈ 1,05 кг

Ссылки

1. Арфкен Г. и Вебер Х. (2012). Математические методы для физиков. Подробное руководство. 7-е издание. Академическая пресса. ISBN 978-0-12-384654-9
2. Расчет cc. Решенные задачи цилиндрических и сферических координат. Получено с: calculo.cc
3. Вайсштейн, Эрик В. «Цилиндрические координаты». Материал из MathWorld — сеть Wolfram Web. Получено с: mathworld.wolfram.com
4. википедия. Цилиндрическая система координат. Получено с: en.wikipedia.com
5. википедия. Векторные поля в цилиндрических и сферических координатах. Получено с: en.wikipedia.com

3 различия между пандемией и эпидемией (и примеры)

Азенапин: характеристики, применение и побочные эффекты этого препарата