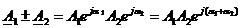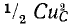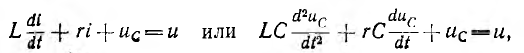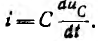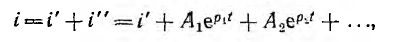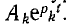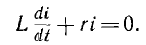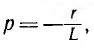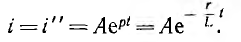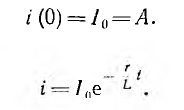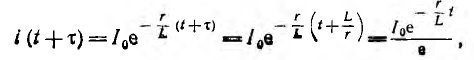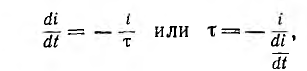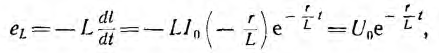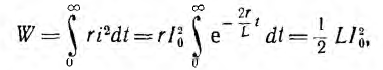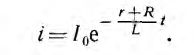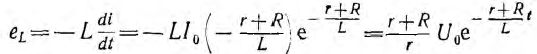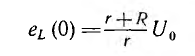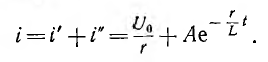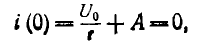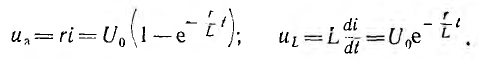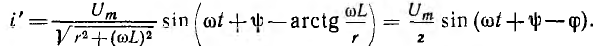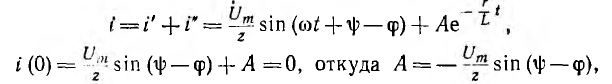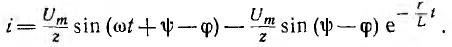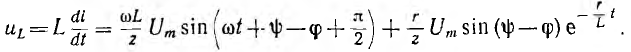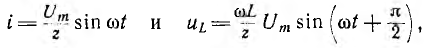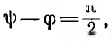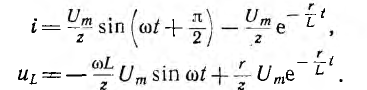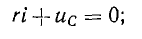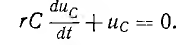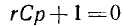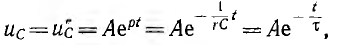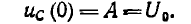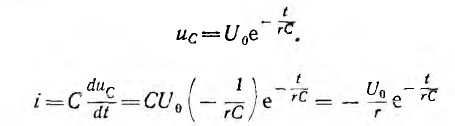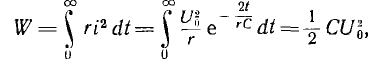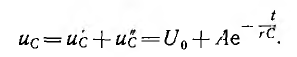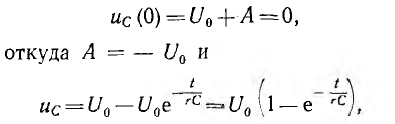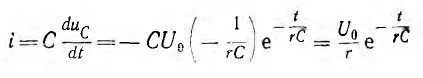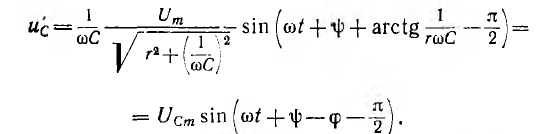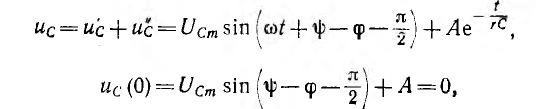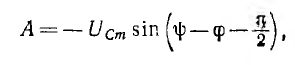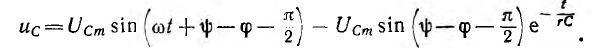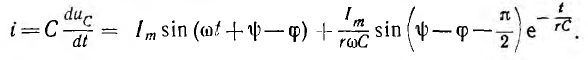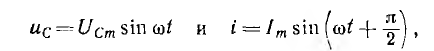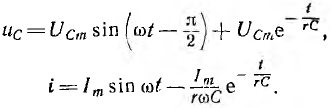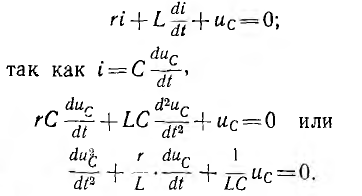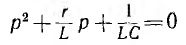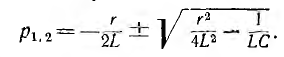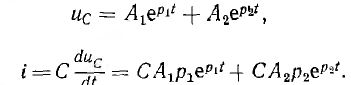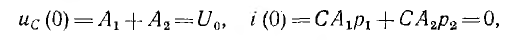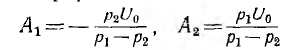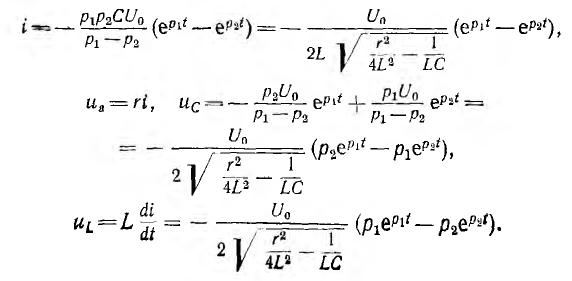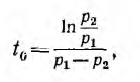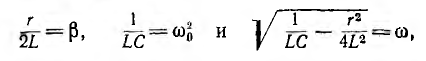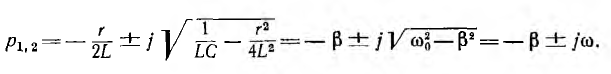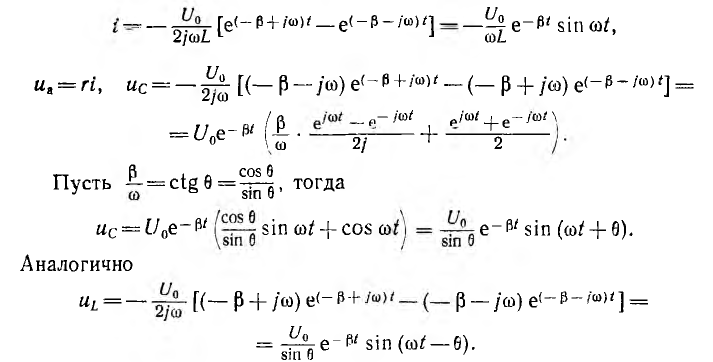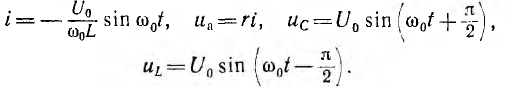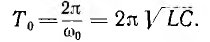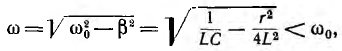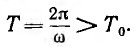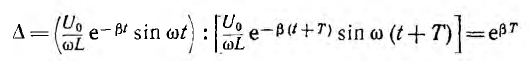Система уравнений кирхгофа для мгновенных значений

№18 Законы Кирхгофа в цепях синусоидального тока. Методы расчета цепей синусоидального тока.

Для мгновенных значений ЭДС, токов и напряжений остаются справедливыми сформулированные ранее законы Кирхгофа.

Первый: в любой момент времени алгебраическая сумма токов в узле электрической цепи равна нулю:

где n — число ветвей, сходящихся в узле

Второй: в любой момент времени в замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме напряжений на всех остальных элементах контура:

где m — число ветвей, образующих контур

Токи, напряжения и ЭДС, входящие в уравнения (2.8) и (2.9), есть синусоидальные функции времени, которые мы рассматриваем как проекции некоторых векторов на оси координат. Так как сложению проекций соответствует сложение векторов и соответствующих им комплексных чисел, то справедливыми будут следующие уравнения, которые можно записывать как для действующих, так и для амплитудных значений.

Законы Киргофа в векторной форме

Законы Киргофа в символической форме

Из сказанного вытекают три возможных подхода к расчету цепей синусоидального тока: выполнение операций непосредственно над синусоидальными функциями времени по уравнениям выше; применение метода векторных диаграмм, использование в расчетах комплексных чисел и уравнений, являющихся основой символического метода.

Пример 2.4. В узле электрической цепи сходятся три ветви (рис. 18.1).

Токи первых двух ветвей известны:

Требуется записать выражение тока i3 и определить показания амперметров электромагнитной системы

Рис. 18.1 — Узел электрической цепи

Непосредственное сложение синусоид:

Сумма двух синусоид одинаковой чыстоты есть тоже синусоида той же частоты. Ее амплитуда и начальная фаза могут быть найдены по известным из математики формулам:

2. Применение метода векторных диаграмм.

В соответствии с первым законом Киргофа в векторной форме для цепи на рис. 18.1 имеем:

В прямоугольной системе координат строим векторы I1m и I2m и находим вектор I3m, равный их сумме (рис. 18.2)

Так как треугольник oab прямоугольный, а сторона ab равна длине вектора I2m, то:

Если треугольник получается не прямоугольным, то применяется теорема косинусов.

Начальная фаза третьего тока равна углу наклона: вектора I3m к горизонтальной оси:

Рис. 18.2 — Векторная диаграмма токов

3. Решение символическим методом

Записываем комплексные амплитуды первого и второго токов:

По первому закону Киргофа в символической форме

Модуль последнего комплексного числа равен амплитуде третьего тока, а агрумент — начальной фазе.

Определяем показания амперметров. Приборы электромагнитной системы показывают действующие значения токов и напряжений, потому:

Обращаем внимание на то, что I1+I2≠I3. Это не ошибка. В цепях синусоидального тока для показаний приборов законы Кирхгофа не справедливы. Можно складывать мгновенные значения токов (синусоидальные функции времени), векторы и комплексные числа, но не численные значения токов и напряжений, не показания приборов.

Следует заметить, что первый из рассмотренных в примере методов из-за громоздкости вычислительных операций с синусоидами практически не применяется.

Метод векторных диаграмм удобен при решении относительно несложных задач.

В символической форме, как будет показано ниже, можно рассчитать сколь угодно сложную линейную цепь.

Закон Ома и законы Кирхгофа для мгновенных значений токов и напряжений. Законы Ома и Кирхгофа в символической и операторной формах.

Первый закон Кирхгофа. Алгебраическая сумма мгновенных токов, притекающих к узлу равна нулю.

Заметим, что первый закон Кирхгофа можно сформулировать и так: сумма мгновенных токов, притекающих к узлу, равна сумме токов, вытекающих из этого узла. В более общей форме: алгебраическая сумма токов, притекающих к произвольному сечению, равна нулю.

Пример. Записать первый закон Кирхгофа для следующего узла (рис. 1.14.2).

Решение. .

Второй закон Кирхгофа для мгновенных величин. Алгебраическая сумма мгновенных падений напряжений в контуре равна алгебраической сумме мгновенных ЭДС в этом контуре.

где n – количество пассивных элементов в контуре;

m – количество источников ЭДС в контуре.

При наличии индуктивности или ёмкости в цепи переменного тока необходимо учитывать их реактивное сопротивление.
В таком случае запись Закона Ома будет иметь вид:

Здесь Z — полное (комплексное) сопротивление цепи — импеданс. В него входит активная R и реактивная X составляющие.
Реактивное сопротивление зависит от номиналов реактивных элементов, от частоты и формы тока в цепи.

С учётом сдвига фаз φ, созданного реактивными элементами, для синусоидального переменного тока обычно записывают Закон Ома в комплексной форме:

— комплексная амплитуда тока. = I_ampe jφ
— комплексная амплитуда напряжения. = U_ampe jφ
— комплексное сопротивление. Импеданс.
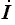
φ — угол сдвига фаз между током и напряжением.
e — константа, основание натурального логарифма.
j — мнимая единица.
I_amp , U_amp — амплитудные значения синусоидального тока и напряжения.

Для последовательно соединенных элементов формула импеданса имеет следующее значение:

При последовательном соединении токи через элементы равны, общее приложенное напряжение будет векторной суммой напряжений на R и C элементах и формула импеданса последовательной цепи будет иметь вид:

Z_ — импеданс последовательной цепи,

R — её активное сопротивление,

XC — ёмкостное сопротивление.

При параллельном соединении напряжения на R и C элементах равны, общий ток будет векторной суммой токов каждого элемента, а фомула импеданса будет следующей:

Операторная запись законов Кирхгофа

При ненулевых начальных условиях II закон Кирхгофа можно записать

Величина, обратная комплексному сопротивлению, – комплексная проводимость:

Законы киргофа в символической форме:

Согласно первому закону Кирхгофа алгебраическая сумма мгновенных значений токов, сходящихся в любом узле схемы, равна нулю:

Подставив вместо i_k в (2.63) Í_ke_jωt и вынеся e_jωt за знак суммы, получим e_jωtΣÍ_k=0. Так как e_jωt не равно нулю при любом t, то:

Уравнение (2.63,а) представляет собой первый закон Кирхгофа в символической форме записи.

Пусть замкнутый контур содержит n ветвей и каждая k- ветвь в общем случае включает в себя источник ЭДС e_k, резистор R_k, индуктивную катушку L_k и конденсатор C_k, по которым протекает ток i_k.

Тогда по второму закону Кирхгофа:

Но каждое слагаемое левой части можно заменить на Í_kZ_k, а каждое слагаемое правой части – на É_k. Поэтому уравнение примет вид:

Уравнение (2.65) представляет собой второй закон Кирхгофа в символической форме записи.

Изображение синусоидальных ЭДС, напряжений и токов с помощью вращающихся векторов и комплексных чисел. Формулы Эйлера для комплексных чисел. Сложение, вычитание, умножение, деление синусоидальных функций времени. Векторная диаграмма.

Геометрические операции с векторами можно заменить алгебраическими операциями с комплексными числами, что существенно повышает точность получаемых результатов.

Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в :

показательной

тригонометрической или

алгебраической — формах.

Например, ЭДС , изображенной на рис. 7 вращающимся вектором, соответствует комплексное число

.

Фазовый угол определяется по проекциям вектора на оси “+1” и “+j” системы координат, как

.

В соответствии с тригонометрической формой записи мнимая составляющая комплексного числа определяет мгновенное значение синусоидально изменяющейся ЭДС:

,

(4)

Рис.2.7. Векторное изображение синусоидальных ЭДС

Рис.2.8. Векторное изображение синусоидальных значений напряжения и тока, имеющих угол сдвига фаз

На рис. 2.9 и 2.10 показано сложение и вычитание векторов на векторных диаграммах. Здесь сложение двух синусоид и , представленных синусоидой , выполнено в виде сложения вращающихся векторов на декартовой плоскости . Аналогично выполняется вычитание векторов ЭДС .

Изображение синусоидальных величин на комплексной плоскости осуществляется комплексными числами.

Данная формула связывает комплексную экспоненту с тригонометрическими функциями:

Перевод комплексных чисел из одной формы в другую можно производить по следующим формулам:

;

;

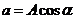
При сложении и вычитании комплексных чисел удобно пользоваться алгебраической формой записи:

При умножении, делении, возведении в степень удобно пользоваться показательной формой

Если комплексное число , то комплексное число называется сопряженным комплексным числом.

Синусоидальное ЭДС можно представить комплексным числом:

Переходные процессы в линейных цепях

Содержание:

Переходные процессы в линейных цепях и их расчет классическим методом:

Процессы в электрических цепях, рассматривавшиеся до сих пор, были установившимися процессами. В этой главе изучаются переходные процессы, которые происходят при всех изменениях режима электрической цепи — включении, выключении, коротком замыкании и т. п. Эти процессы не могут протекать мгновенно, так как невозможны мгновенные изменения энергии, запасенной в электромагнитном поле цепи.

В цепях с сосредоточенными параметрами энергия запасается в емкостях в виде энергии

Для расчета переходных процессов в цепях составляется система уравнений по законам Ома и Кирхгофа для мгновенных значений напряжений и токов. Эта система приводится к одному уравнению для одного из напряжений или токов, которое в общем случае линейных цепей будет линейным обыкновенным дифференциальным уравнением. Порядок этого уравнения можно определить из упрощенной схемы цепи, объединяя индуктивности и, соответственно, емкости, соединения между которыми являются последовательными и параллельными или приводятся к ним. Тогда искомый порядок равен числу независимых начальных условий для токов индуктивностей и напряжений на емкостях упрощенной схемы. Например, если три индуктивности соединены в звезду, объединить их нельзя, но можно задать только два независимых начальных условия в виде токов двух индуктивностей, так как ток третьей определяется через первые два. Для цепи с последовательным соединением r, L и С (см. рис. 7.1, a) уравнение, связывающее напряжение и цепи с током i, будет второго порядка, так как начальные значения i и u_с могут быть заданы независимо друг от друга:

так как

Как известно из математики, решение линейных дифференциальных уравнений с постоянными коэффициентами представляет собой сумму двух решений, например,

где i’ — частное решение неоднородного уравнения, a i» — общее решение однородного уравнения, выраженное через постоянные интегрирования 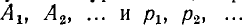— корни характеристического уравнения для случая, когда все корни различны.

Частное решение i» неоднородного уравнения определяется видом функции, стоящей в правой части уравнения, и поэтому называется принужденным. Для цепей с заданными постоянными или периодическими напряжениями (токами) источников энергии принужденное решение совпадает с установившимися значениями искомых величин и определяется известными из предыдущего методами расчета цепей.

Общее решение i» однородного уравнения описывает процесс, происходящий без воздействия внешних источников за счет изменения запаса энергии, накопленной в цепи до начала переходного процесса; оно имеет одинаковый вид для любого переходного процесса в данной цепи. Это решение называют свободной составляющей переходного процесса. Так как запасенная в цепи энергия при отсутствии внешних источников будет постепенно расходоваться, свободная составляющая с течением времени уменьшится до нуля. Математически это соответствует отрицательным вещественным корням или отрицательным вещественным частям комплексных корней р_к характеристического уравнения, что вызывает убывание во времени функций вида

Сумма принужденной и свободной составляющих 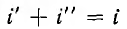представляет собой искомую величину, в данном примере ток; она называется переходной.

Исходя из выражения для переходной величины, определяют постоянные интегрирования 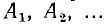из начальных условий — значений напряжений u_с (0) на емкостях и токов i_L (0) в индуктивностях, которые имели место до начала переходного процесса и, в соответствии со сказанным о невозможности скачков, будут теми же и в начальный момент переходного процесса.

Переходный ток превращается в принужденный, когда затухнет свободный ток. Математически строго это наступит при t — оо, практически время переходных процессов в большинстве электрических цепей исчисляется долями секунды.

В переходном процессе при коротком замыкании цепи свободная составляющая равна переходной величине, так как тогда правая часть уравнения, например приложенное к цепи напряжение, а следовательно, и принужденная составляющая переходной величины будут равны нулю. Поэтому при изучении переходных процессов в различных цепях целесообразно сначала рассмотреть их короткое замыканне, а определенный при этом общий вид переходной величины использовать, как свободную составляющую для других переходных процессов.

Таким образом, методика расчета переходных процессов, называемая классической, состоит в составлении дифференциальных уравнений для цепи, их решении и определении постоянных интегрирования из начальных условий.

Переходные процессы в цепи с последовательным соединением сопротивления и индуктивности

Короткое замыкание цепи:

При коротком замыкании цепи с последовательным соединением r и L (рис. 15.1, а) уравнение переходного тока i, равного в этом случае свободному току i», имеет вид:

Характеристическое уравнение Lp + r = О

имеет корень

Если до момента короткого замыкания по цепи шел постоянный ток 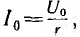, где U₀ — постоянное напряжение цепи (рис. 15.1, б),

это значение тока сохранится и для первого мгновения после замыкания цепи, откуда определяется постоянная интегрирования:

следовательно,

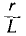
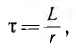
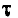
Это выражение изображается затухающей кривой — экспонентой, ордината которой при t = 0 равна I₀. Уменьшение тока i происходит тем быстрее, чем больше коэффициент затухания или чем меньше обратная величина имеющая размерность времени и называемая постоянной времени. По истечении времени с любого момента t переходный ток

т. е. в е = 2,718 . раз меньше своего первоначального значения. Так как

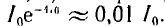
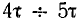
постоянная времени равна длине подкасательной в любой точке кривой i (см. рис. 15.1, б). За время, равное 4,6 т, переходный ток затухает до значения Так как переходный ток при коротком замыкании равен свободному току и для других переходных процессов в этой цепи, для большинства инженерных задач можно считать, что переходный процесс за время практически заканчивается. Постоянная времени цепей обычно невелика; для катушек без ферромагнитных сердечников она составляет десятые доли секунды.

В короткозамкнутой цепи появляется э. д. с. самоиндукции

поддерживающая ток. Эта э. д. с. возникает при коротком замыкании цепи скачкообразно, принимая значение U₀ при t= 0(см. рис. 15.1 б).

Энергия, расходуемая на нагрев сопротивления г цепи за время переходного процесса

равна энергии, запасенной в индуктивности до замыкания цепи.

Процессы будут протекать аналогично и при коротком замыкании цепи переменного тока, но тогда I₀ будет мгновенным значением тока цепи в момент замыкания.

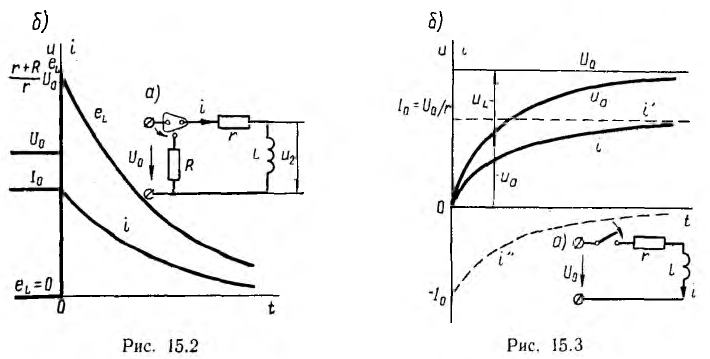
Замыкание цепи на добавочное сопротивление

Предполагается, что цепь r, L, отключаясь от источника напряжения U₀, замыкается на добавочное сопротивление R без предварительного размыкания цепи, что можно осуществить с помощью переключателя, схематически показанного на рис. 15.2, а. Для тока цепи после переключения может быть использовано полученное в п. 1 выражение, но сопротивление цепи теперь равно r+R:

Из-за уменьшения постоянной времени ток будет затухать быстрее (рис. 15.2, б). Э. д. с. самоиндукции

поддерживает в цепи ток 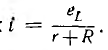Значение э. д. с. в первый момент после переключения

больше напряжения U₀ во столько раз, во сколько увеличилось сопротивление цепи. Это явление называется перенапряжением.

Казалось бы, что процесс размыкания цепи можно рассматривать как замыкание цепи на добавочное сопротивление R = 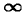; но при этом перенапряжение, а следовательно, и напряжение на выключателе должно в первый момент равняться бесконечности, чего быть не может. В действительности под воздействием возрастающего напряжения произойдет пробой промежутка между контактами выключателя, и в цепь окажется включенным увеличивающееся по мере разведения контактов сопротивление электрической дуги. Цепь и ее уравнение становятся нелинейными, и расчет не может быть выполнен элементарным путем. Эта задача является основной в теории выключающей аппаратуры.

Включение цепи на постоянное напряжение

При включении цепи r, L на постоянное напряжение U₀ (рис. 15.3, а) принужденный ток 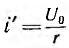переходный ток

Ток до переходного процесса, а следовательно, и в первый момент после включения равен нулю:

отсюда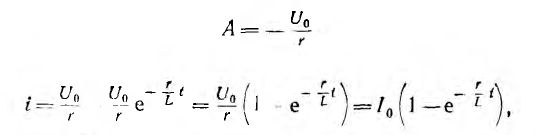

т. е. переходный ток постепенно нарастает до своего окончательного значения I₀ и тем медленней, чем больше постоянная времени 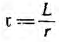(рис. 15.3, б); здесь показаны также принужденная и свободная составляющие переходного тока.

Напряжения на участках цепи

Следовательно, в первый момент напряжение цепи целиком сосредоточивается на индуктивности и затем постепенно переходит на сопротивление.

Изменение сопротивления цепи

Пусть в цепи r + R, L (рис. 15.4, а) рубильник то замыкается, шунтируя резистор R, то размыкается, вновь включая этот резистор, причем промежутки между переключениями больше времени практического установления процесса.

Тогда принужденный ток меняется от значения

и переходный ток после замыкания рубильника

После размыкания переходный ток

График изменения тока в цепи изображен на рис. 15.4, в-, процесс осле размыкания рубильника устанавливается быстрей, так как постоянная времени цепи меньше, чем после замыкания.

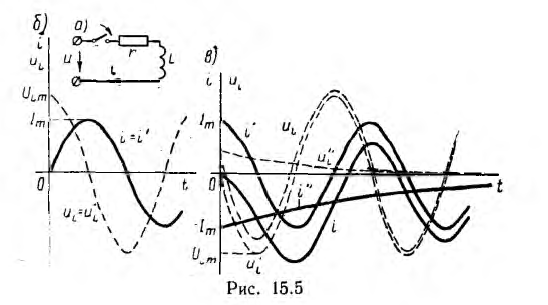
Включение цепи на синусоидальное напряжение

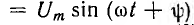
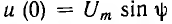
Пусть цепь r, L включается на синусоидальное напряжение (рис. 15.5, а). Тогда значение напряжения в момент включения определяется величиной начальной фазы ψ, которая в этом случае называется также фазой включения.

Переходное напряжение на сопротивлении пропорционально току u_a = ri, а на индуктивности

При включении в момент, когда принужденный ток равен нулю, например при 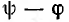= 0,

т. е. свободного тока и свободных напряжений на участках цепи нет, и сразу после включения наступает установившийся процесс (рис. 15.5, б).

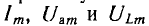
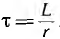
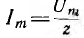
В общем случае на синусоидальные установившиеся напряжения на участках цепи и ток налагаются свободные составляющие, значения которых уменьшаются по показательному закону. В результате ток и напряжения u_а и u_L в течение некоторых промежутков времени могут превосходить их максимальные значения при установившемся режиме, т. е. могут возникнуть большой ток, называемый сверхтоком, и перенапряжения. Их величина зависит от фазы включения ψ и от постоянной времени , определяющих соответственно, начальные значения свободных составляющих и скорость их уменьшения. Так, при включении в момент, когда принужденный ток получает максимальное значение например при

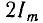
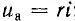
При большой постоянной времени получается большой сверхток (рис. 15.5, в), однако он не может превзойти двойную амплитуду установившегося тока. Аналогично поведение , перенапряжение же для u_L меньше, так как в этом случае r и u_L малы.

Переходные процессы в цепи с последовательным соединением сопротивления и емкости

Короткое замыкание цепи:

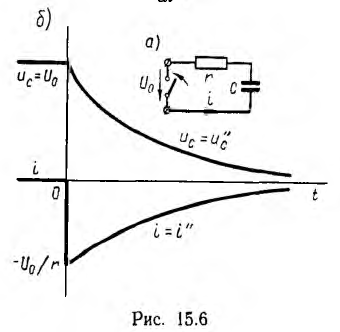
При коротком замыкании цепи с последовательным соединением r и С (рис. 15.6, а)

так как 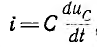, уравнение для переходного емкостного напряжения u_с. равного в этом случае его свободному значению u»_с, будет

корень 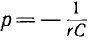, тогда

где 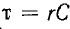— постоянная времени этой цепи.

Если начальное напряжение на емкости было равно U₀ оно сохранится и для первого мгновения после замыкания, откуда определится постоянна интегрирования:

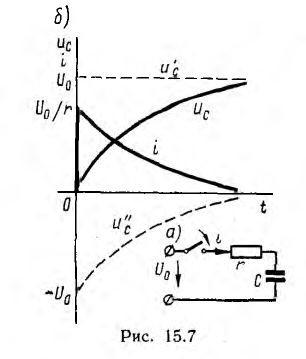
Следовательно, напряжение на емкости убывает по экспоненте (рис. 15.6, б):

Ток

возникает при коротком замыкании цепи скачкообразно, принимая значение 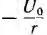затем убывает по тому же экспоненциальному закону.

Так как это ток разряда, знак его отрицательный. Энергия, расходуемая на нагрев сопротивления r за время переходного процесса,

т. е. равна энергии, запасенной в емкости до замыкания цепи.

Включение цепи на постоянное напряжение

При включении цепи r, С на постоянное напряжение U₀ (рис. 15.7, а) емкость будет заряжаться до принужденного напряжения u’_с = U₀. Тогда переходное напряжение

Напряжение на емкости до переходного процесса, а следовательно, и в первый момент после включения равно нулю:

т. е. напряжение на емкости постепенно нарастает до своего окончательного значения и тем медленней, чем больше постоянная времени 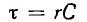(рис. 15.7, б).

три включении цепи возникает скачком и изменяется по тому же некартельному закону, что и ток разряда, но имеет положительный знак. Следовательно, энергия, расходуемая на нагрев сопротивления за время переходного процесса, независимо от величины r будет такой же как и в случае разряда, т. е. 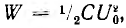, и равна энергии, которая запасается в емкости при ее зарядке.

Интересно отметить, что при зарядке конденсатора постоянны током I₀, например от источника тока с пренебрежимо малой внутренней проводимостью, время зарядки до заданного напряжения U было бы 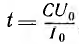т. е. конечным, а потери в сопротивлении при малом r будут малы.

Включение цепи на синусоидальное напряжение

При включении цепи r, С на синусоидальное напряжение 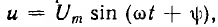где ψ — фаза включения (рис. 15.8, а), принужденное напряжение на емкости

откуда постоянная интегрирования

переходный ток цепи

При включении в тот момент, когда принужденное напряжение на емкости равно нулю, например при .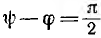

т. е. сразу после включения наступает установившийся процесс.

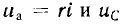
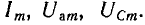
В общем случае на синусоидальные установившиеся напряжение на емкости и ток цепи налагаются свободные составляющие, значения которых уменьшаются по показательному закону. В результате ток i и напряжения в течение некоторых промежутков времени могут превосходить максимальные значения Величины сверхтока и перенапряжений зависят от фазы включения ψ и от постоянной времени rС, определяющих, соответственно, начальные значения свободных составляющих и скорость их уменьшения.

При включении в тот момент, когда принужденное напряжение на емкости получает максимальное значение U_cm, а принужденный ток равен нулю, например при = О,

В этом случае при большой постоянной времени rС получается большое перенапряжение на емкости, равное в пределе двойной амплитуде 2U_cm установившегося напряжения на емкости, но малый сверхток (рис. 15.8, б). При малой постоянной времени может получиться сверхток 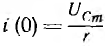, во много раз превосходящий амплитуду I_m тока установившегося режима, но тогда перенапряжения на емкости практически не будет (рис. 15.8, в).

Переходные процессы в цепи с последовательным соединением сопротивления, индуктивности и емкости

Короткое замыкание цепи:

Как было показано, решение задачи короткого замыкания до определения постоянных интегрирования дает выражение для свободной составляющей тока или напряжения в цепи.

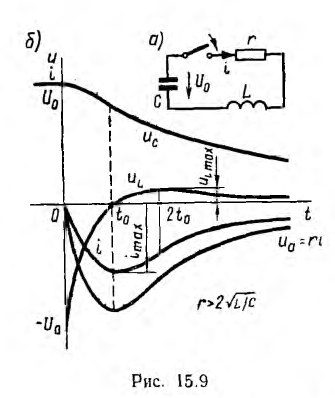
Пусть емкость, заряженная до напряжения U₀ замыкается на цепи последовательным соединением сопротивления и индуктивности (рис. 15.9, а). Тогда уравнение по второму закону Кирхгофа будет одно родным:

имеет два корня:

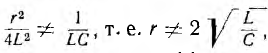
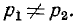
Если корни будут различными: В этом случае решение дифференциального уравнения

а ток цепи

В момент t = 0 напряжение на емкости и ток индуктивности, равный току всей цепи, будут такими же, как и до замыкания:

откуда постоянные интегрирования

и, следовательно, ток и напряжения на участках будут:

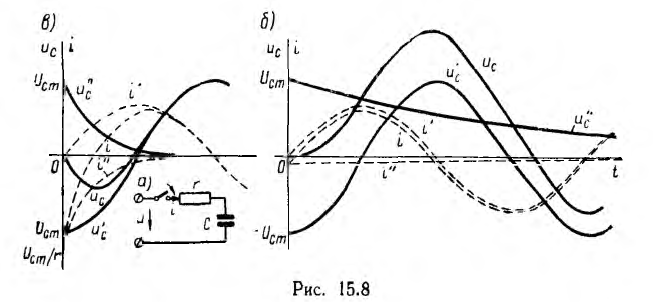
Характер переходного процесса зависит от соотношения между параметрами r, L и С цепи.

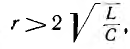
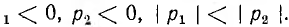
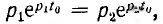
1. Если корни р₁ и р₂ будут вещественными, причем Этo значит, что все вычисленные выше величины состоят из алгебраической суммы двух экспонент, имеющих разные знаки, причем первая экспонента затухает медленней, чем вторая. В результате (рис. 15.9, б) напряжение конденсатора, начиная с U₀, непрерывно убывает, оставаясь всегда положительным, так как его первая экспонента положительная и больше второй отрицательной. Ток i цепи и напряжение u_а = ri на сопротивлении, начинаясь о нуля, всегда отрицательны, что соответствует току разряда. Напряжение u_L на индуктивности возникает скачком, принимая значение —U₀ проходит через нуль в момент t₀ при равенстве значений своих экспонент, т. е. при откуда

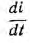
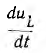
и затем становится положительным. Так как u_L пропорционально производной в момент t = t₀ абсолютное значение тока проходит через максимум. Приравняв производную нулю, можно видеть, что u_L имеет максимум при t = 2t₀ (см. рис. 15.9,6). Рассмотренный вид разряда называется апериодическим.

Энергетическая сторона апериодического процесса заключается в следующем.

Так как напряжение u_с непрерывно уменьшается, емкость отдает энергию. Индуктивность с ростом тока накапливает энергию, но, начиная с t = t0, ток убывает и индуктивность постепенно отдает энергию. В течение всего процесса сопротивление рассеивает потребляемую им энергию.

2. Пусть 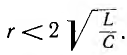. Введя обозначения

можно переписать выражение для корней характеристического уравнения следующим образом:

Так как ω — число вещественное, корни р₁ и р₂ будут комплексными.

После подстановки значений р₁ и р₂ и очевидных преобразований выражения для тока и напряжений на участках получат вид:

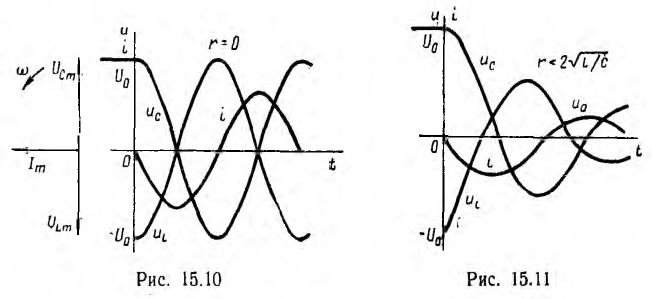
Ток и напряжения цепи, в которой r= 0 и, следовательно, β = 0, 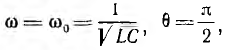будут:

Следовательно, если бы в цепи не происходило рассеяние энергии, ток и напряжения на участках были бы синусоидальными функциями времени, т. е. имели бы место так называемые собственные незатухающие колебания, угловая частота которых равна резонансной частоте этой цепи 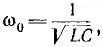а период определяется по формуле Томсона:

Для незатухающих колебаний на рис. 15.10 изображены векторная диаграмма и график мгновенных значений тока и напряжений на индуктивности и емкости, которые аналогичны имеющим место при резонансе в цепи с последовательным соединением r, L и С (см. рис. 7.4). Следовательно, и здесь происходит полный обмен энергиями между С и L.

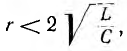
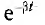
Если в цепи есть сопротивление, разряд, как видно из приведенных выражений для тока и напряжений, также носит колебательный характер, но амплитуды тока и напряжений постепенно уменьшаются, так какс ростом t стремится к нулю.

Угловая частота этих собственных затухающих колебаний

Период собственных затухающих колебаний

Отношение мгновенного значения какой-либо величины, например тока, к значению этой величины через период Т:

называется декрементом колебания.

На рис. 15.11 изображен график мгновенных значений тока и напряжений для затухающих колебаний. Энергетический процесс заключается, в основном, в обмене энергиями между емкостью и индуктивностью с непрерывным рассеянием энергии сопротивлением. Переходный процесс закончится, когда энергия 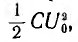первоначально запасенная в емкости, будет целиком рассеяна.

3. Если 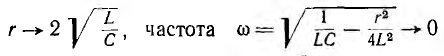и стоящая

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.