Система уравнений максвелла в веществе

Лекция 14. Энергия магнитного поля. Уравнения Максвелла в веществе

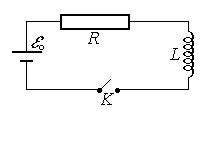Рассмотрим цепь, содержащую активное сопротивление R, катушку индуктивности L и источник эдс e_o (рис.49). При замыкании ключа К ток начнет возрастать, вследствие этого появится эдс самоиндукции e_s. По закону Ома, RI=e_o+e_s, следовательно,

Умножая обе части на Idt, получим

где левая часть представляет собой работу сторонних сил dА*, первое слагаемое справа — джоулево тепло. Последнее слагаемое равно IdФ (так как e_S=-dФ/dt). Таким образом,

следовательно, dА*>dQ, а часть работы (IdФ=ILdI) совершается против эдс самоиндукции. За счет этой работы контур накапливает энергию, которую вычислим, интегрируя последнее выражение

W = 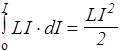. (150)

Выразим энергию магнитного поля через В. Действительно, L=mm_on 2 V, как индуктивность длинного соленоида, поэтому

W = .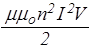

Но так как для соленоида В=mm_onI, и B=mm_oH, следовательно,

,

где слева стоит энергия поля в единице объема, т.е. плотность энергии. Расчет показывает, что это верно и в векторном виде

, (151)

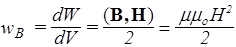
где w_B — плотность энергии магнитного поля, которая для неоднородного поля равна производной: w_B=dW/dV.

Уравнения Максвелла для среды в интегральной форме. Выпишем уравнения Максвелла для среды в интегральной форме в виде таб.2, где в правой колонке дадим их формулировки.

Уравнения Максвелла для среды в интегральной форме. Таблица 2

I		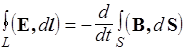Циркуляция вектора Е по любому замкнутому контуру равна минус производной по времени от магнитного потока через любую поверхность, ограниченную этим контуром. Под Е понимается как вихревое, так и электростатическое поле
II		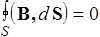Поток вектора В сквозь любую замкнутую поверхность равен нулю
III		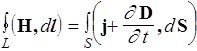Циркуляция вектора Н по любому замкнутому контуру равна полному току (проводимости и смещения) через любую поверхность, ограниченную данным контуром
IV		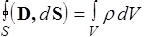Поток вектора D сквозь любую замкнутую поверхность равен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью

По форме уравнения Максвелла для вещества и вакуума идентичны. Однако для описания электрического и магнитного полей в вакууме введение векторов D и Н не являлось принципиально необходимым. Рассуждения, с помощью которых мы пришли к уравнениям Максвелла, не могут претендовать на роль доказательств. Эти уравнения в общем случае нельзя «вывести» — они являются основными аксиомами электродинамики.

Уравнения Максвелла в веществе в дифференциальной форме. В принципе эти уравнения уже были нами сформулированы. Выпишем их еще раз, используя параллельно оператор набла

I. , .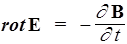

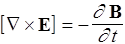
II. div B= 0, .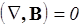

III. , ,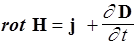

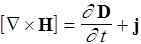
IV. div D =r, (Ñ,D) = r.

В этой форме уравнения утверждают следующее. Электрическое поле может возникнуть по двум причинам. Во-первых, его источниками являются электрические заряды (и сторонние, и связанные — это следует из последнего уравнения, где D=e_оЕ+Р и (Ñ,P)=-r’, следовательно, (Ñ,E)

r+r’); во-вторых,- переменное магнитное поле. Как видно из уравнения III, магнитное поле может порождаться движущимися зарядами и переменными электрическими полями: так как Н=m₀B—J и [Ñ´J]=j‘, следовательно, [Ñ´B]

j+j’+¶Р/¶t+e_о¶E/¶t. Первые три тока связаны с движением зарядов, последний — с изменяющимся во времени электрическим полем Е. Источников магнитных зарядов не существует (это показывает уравнение II).

Материальные уравнения. Фундаментальные уравнения Максвелла не составляют полной системы уравнений: их недостаточно для нахождения полей по заданным распределениям зарядов и токов. Для этого их необходимо дополнить соотношениями, характеризующими свойства среды. Эти соотношения называются материальными уравнениями.

Материальные уравнения просты (и нам уже знакомы) в случае достаточно слабых электромагнитных полей, медленно меняющихся в пространстве и во времени. Для изотропных сред, несодержащих сегнетоэлектриков и ферромагнетиков, материальные уравнения имеют вид

D= ee_oE, B= mm_oH, j= s(E+ E*).

Величины e, m и s характеризуют электрические и магнитные свойства среды; E* — напряженность поля сторонних сил.

Уравнения Максвелла

Уравнения Максвелла — это 4 уравнения, которые описывают, как электрические и магнитные поля распространяются и взаимодействуют; т.е. эти уравнения (правила или даже законы) описывают процессы/взаимодействия электромагнетизма.

Эти правила описывают, как проходит управление поведением электрических и магнитных полей. Уравнения Максвелла показывают, что электрический заряд (положительный и отрицательный):

1. Порождает электрическое поле (также если заряд изменяется со временем, то он вызывает появление электрического поля).
2. В дальнейшем он вызывает появление магнитного поля.

Уравнения Максвелла в дифференциальной форме

Уравнение 1: Закон Гаусса или Теорема Гаусса

Дивергенция электрического поля равняется плотности заряда. Существует вязь между электрическим полем и электрическим зарядом.

Дивергенция в физике показывает, насколько данная точка пространства является источником или потребителем потока поля.

Очень кратко: Электрические поля расходятся от электрических зарядов: электрический заряд создаёт поле вокруг себя и, таким образом, действует как источник электрических полей. Это можно сравнить с краном, который является источником воды.

Ещё закон Гаусса говорит о том, что отрицательные заряды действуют как сток для электрических полей (способ, как вода стекает через отверстие стока). Это означает, что линии электрического поля имеют начало и поглощаются при электрическом заряде.

Заряды с одинаковым знаком отталкиваются друг от друга, а противоположные заряды притягиваются друг к другу (если есть два положительных заряда, они будут отталкиваться; а если есть один отрицательный и один положительный, они будут притягиваться друг к другу).

Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)

Можно создать электрическое поле, изменив магнитное поле.

Очень кратко: Закон Фарадея гласит, что изменяющееся магнитное поле внутри контура вызывает индуцированный ток, который возникает из-за силы или напряжения внутри контура. Это значит:

1. Электрический ток порождает магнитные поля, а эти магнитные поля (вокруг цепи) вызывают электрический ток.
2. Изменяющееся во времени магнитное поле вызывает распространение электрического поля.
3. Циркулирующее во времени электрическое поле вызывает изменение магнитного поля во времени.

Уравнение 3: Закон Гаусса для магнетизма

Дивергенция магнитного потока любой замкнутой поверхности равна нулю. Магнитного монополя не существует.

Закон Гаусса для магнетизма утверждает (очень кратко):

1. Магнитных монополей не существует.
2. Расхождение полей B или H всегда равно нулю в любом объёме.
3. На расстоянии от магнитных диполей (это круговой ток) магнитные поля текут по замкнутому контуру.

Уравнение 4: Закон Ампера

Магнитное поле создаётся с помощью тока или изменяющегося электрического поля.

Очень кратко: Электрический ток порождает магнитное поле вокруг тока. Изменяющийся во времени электрический поток порождает магнитное поле.

Уравнения Максвелла в интегральной и дифференциальной форме

Вспомним сначала в дифференциальной форме и следом будет в интегральной форме.

Уравнение 1: Закон Гаусса (Теорема Гаусса)

Это же уравнение в интегральной форме:

Поток вектора электрической индукции D через любую замкнутую поверхность равняется сумме свободных зарядов, охваченных этой поверхностью. Электрическое поле создаётся нескомпенсированными электрическими зарядами (это те, что создают вокруг себя своё собственное электрическое поле).

Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)

И это же уравнение в интегральной форме:

Циркуляция вектора напряжённости Е вихревого электрического поля (по любому замкнутому контуру) равняется скорости изменения магнитного потока через площадь контура (S) с противоположным знаком.

Уравнение 3: Закон Гаусса для магнетизма

И это же уравнение в интегральной форме:

Силовые линии магнитного поля замкнуты, т.к. поток вектора индукции В магнитного поля через любую замкнутую поверхность равняется нулю.

Уравнение 4: Закон Ампера

И это же уравнение в интегральной форме:

Циркуляция вектора напряжённости Н магнитного поля по замкнутому контуру равняется алгебраической сумме токов, которые пронизывают этот контур. Магнитное поле создаётся не только током проводимости, но и переменным электрическим полем.

9.3. Уравнения Максвелла

Четыре уравнения, соответствующие нашим (модифицированным) утверждениям, называются уравнениями Максвелла в интегральной форме.

Выпишем их все рядом еще раз:

Чтобы получить уравнения Максвелла в среде, надо произвести замену:

,

то есть указать связь (так называемые «материальные» уравнения) между напряженностями и индукциями: и и дополнить систему уравнением закона Ома

.

Отметим, что приведенными выше простейшими соотношениями можно пользоваться не всегда. Ситуация заметно сложнее в присутствии таких веществ как сегнетоэлектрики, пьезоэлектрики, ферромагнетики, вещества анизотропные и тому подобное. Здесь наша цель показать, как формируется полная система уравнений, позволяющая (с учетом начальных и граничных условий, разумеется) рассчитать электромагнитное поле.

От уравнений в интегральной форме можно с помощью теорем векторного анализа перейти к уравнениям в дифференциальной форме, связывающим значения полей и и их пространственных и временных производных со значениями плотностей заряда и тока. Этими уравнениями мы пользоваться не будем, но все же приведем их хотя бы как часть шутки, опубликованной в одном из журналов в дни юбилея Максвелла:

Непонятные значки div (читается «дивергенция») и rot (читается «ротор») — это особые операции дифференцирования, выполняемые над векторными полями. Дивергенция — по латыни «расхождение». Эта операция описывает конфигурацию силовых линий типа «ежа», расходящихся из точек, где имеются электрические заряды. Слово «ротор» в переводе не нуждается, оно явно ассоциируется с вращением. Эта операция описывает вихревые поля (кольцеобразные — замкнутые силовые линии) вокруг их источников — токов или других полей, меняющихся во времени.

Четыре интегральных уравнения и четыре дифференциальных эквивалентны. Максвелл показал, что все явления электромагнетизма можно полностью описать этими четырьмя уравнениями, являющимися обобщением экспериментальных фактов.

В приведенной шутке упоминался свет. Действительно, свет — это электромагнитное излучение определенного диапазона частот. Предсказание электромагнитных волн стало одним из величайших достижений теории Максвелла. Представим себе, что заряды и токи отсутствуют. Посмотрим на уравнения Максвелла в дифференциальной форме. Видно, что если поля не статические, но зависят от времени, то имеется вихревое электрическое и магнитные поля (соответствующие роторы отличны от нуля). Распространение полей без зарядов и токов — это и есть электромагнитные волны. И можно углядеть в уравнениях намек на скорость их распространения: туда входит комбинация e₀m₀, через которую может быть выражена скорость света в вакууме (см. (6.3))

Но об этом — позже, в следующей части нашего курса.

В заключение же этой части процитируем слова Г. Герца об уравнениях Максвелла:

«Трудно избавиться от чувства, что эти математические формулы живут независимой жизнью и обладают своим собственным интеллектом, что они мудрее, чем мы сами, мудрее даже, чем их первооткрыватели, и что мы извлекаем из них больше, чем было заложено в них первоначально».

Пример использования уравнений Максвелла

Определить величину магнитного поля в зазоре конденсатора как функцию r расстояния от оси симметрии (рис. 9.13)

Рис. 9.13. Конденсатор с круглыми пластинами в процессе зарядки

Решение

Запишем уравнение (9.13) для контура, показанного на Рис. 9.3 штрихованной линией. Интегрируя, получим

Очевидно, что магнитное поле не равно нулю только благодаря наличию меняющегося со временем электрического поля. В свою очередь, изменение электрического поля обусловлено увеличением заряда на обкладках конденсатора. Эту связь получим из соотношений

Согласно полученной формуле,

что явно неверно. В чем ошибка?

ОТВЕТ: формула справедлива только при .

Дополнительная информация