Система уравнений матрицы и определители
ОПРЕДЕЛЕНИЕ МАТРИЦЫ. ВИДЫ МАТРИЦ
Матрицей размером m×n называется совокупность m·n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов. Эту таблицу обычно заключают в круглые скобки. Например, матрица может иметь вид:
Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В.
В общем виде матрицу размером m×n записывают так

Числа, составляющие матрицу, называются элементами матрицы. Элементы матрицы удобно снабжать двумя индексами aij: первый указывает номер строки, а второй – номер столбца. Например, a23 – элемент стоит во 2-ой строке, 3-м столбце.
Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы. В приведённых выше примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая матрица – её порядок 1.
Матрица, в которой число строк не равно числу столбцов, называется прямоугольной. В примерах это первая матрица и третья.
Различаются также матрицы, имеющие только одну строку или один столбец.
Матрица, у которой всего одна строка 
Матрица, все элементы которой равны нулю, называется нулевой и обозначается (0), или просто 0. Например,

Главной диагональю квадратной матрицы назовём диагональ, идущую из левого верхнего в правый нижний угол.
Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей.

Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональной матрицей. Например, 

Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой E. Например, единичная матрица 3-го порядка имеет вид 
ДЕЙСТВИЯ НАД МАТРИЦАМИ
Равенство матриц. Две матрицы A и B называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны aij = bij. Так если 

Транспонирование. Рассмотрим произвольную матрицу A из m строк и n столбцов. Ей можно сопоставить такую матрицу B из n строк и m столбцов, у которой каждая строка является столбцом матрицы A с тем же номером (следовательно, каждый столбец является строкой матрицы A с тем же номером). Итак, если 

Эту матрицу B называют транспонированной матрицей A, а переход от A к B транспонированием.
Таким образом, транспонирование – это перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A, обычно обозначают A T .
Связь между матрицей A и её транспонированной можно записать в виде 
Например. Найти матрицу транспонированную данной.
Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C, которая определяется по правилу, например,
Примеры. Найти сумму матриц:
.
— нельзя, т.к. размеры матриц различны.
.
Легко проверить, что сложение матриц подчиняется следующим законам: коммутативному A+B=B+A и ассоциативному (A+B)+C=A+(B+C).
Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы A на число k есть новая матрица, которая определяется по правилу 

Для любых чисел a и b и матриц A и B выполняются равенства:
.
.
- Найти 2A-B, если
,
.


Матрицу C найти нельзя, т.к. матрицы A и B имеют разные размеры.
Умножение матриц. Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением матрицы A не матрицу B называется новая матрица C=AB, элементы которой составляются следующим образом:

Таким образом, например, чтобы получить у произведения (т.е. в матрице C) элемент, стоящий в 1-ой строке и 3-м столбце c13, нужно в 1-ой матрице взять 1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на соответствующие элементы столбца и полученные произведения сложить. И другие элементы матрицы-произведения получаются с помощью аналогичного произведения строк первой матрицы на столбцы второй матрицы.
В общем случае, если мы умножаем матрицу A = (aij) размера m×n на матрицу B = (bij) размера n×p, то получим матрицу C размера m×p, элементы которой вычисляются следующим образом: элемент cij получается в результате произведения элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B и их сложения.
Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.
Другим важным случаем является умножение матрицы–строки на матрицу–столбец, причём ширина первой должна быть равна высоте второй, в результате получим матрицу первого порядка (т.е. один элемент). Действительно,

- Пусть

Найти произведение матриц.

 .
. — нельзя, т.к. ширина первой матрицы равна 2-м элементам, а высота второй – 3-м.
— нельзя, т.к. ширина первой матрицы равна 2-м элементам, а высота второй – 3-м.

Таким образом, эти простые примеры показывают, что матрицы, вообще говоря, не перестановочны друг с другом, т.е. A∙B ≠ B∙A. Поэтому при умножении матриц нужно тщательно следить за порядком множителей.
Можно проверить, что умножение матриц подчиняется ассоциативному и дистрибутивному законам, т.е. (AB)C=A(BC) и (A+B)C=AC+BC.
Легко также проверить, что при умножении квадратной матрицы A на единичную матрицу E того же порядка вновь получим матрицу A, причём AE=EA=A.
Можно отметить следующий любопытный факт. Как известно произведение 2-х отличных от нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение 2-х не нулевых матриц может оказаться равным нулевой матрице.
Например, если 

Пусть дана матрица второго порядка – квадратная матрица, состоящая из двух строк и двух столбцов 
Определителем второго порядка, соответствующим данной матрице, называется число, получаемое следующим образом: a11a22 – a12a21.
Определитель обозначается символом 
Итак, для того чтобы найти определитель второго порядка нужно из произведения элементов главной диагонали вычесть произведение элементов по второй диагонали.
Примеры. Вычислить определители второго порядка.
.
- Вычислить определитель матрицы D, если D= -А+2В и
Аналогично можно рассмотреть матрицу третьего порядка и соответствующий ей определитель.
Определителем третьего порядка, соответствующим данной квадратной матрице третьего порядка, называется число, обозначаемое и получаемое следующим образом:

Таким образом, эта формула даёт разложение определителя третьего порядка по элементам первой строки a11, a12, a13 и сводит вычисление определителя третьего порядка к вычислению определителей второго порядка.
Примеры. Вычислить определитель третьего порядка.
.
.
- Решите уравнение.
.

Аналогично можно ввести понятия определителей четвёртого, пятого и т.д. порядков, понижая их порядок разложением по элементам 1-ой строки, при этом знаки «+» и «–» у слагаемых чередуются.
Итак, в отличие от матрицы, которая представляют собой таблицу чисел, определитель это число, которое определённым образом ставится в соответствие матрице.
Методы решения систем линейных алгебраических уравнений (СЛАУ) с примерами
Содержание:
Методы решения систем линейных алгебраических уравнений (СЛАУ)
Метод Крамера
Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение
Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы
Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на 
Второй столбец умножим на 



Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е.
Определение: Определитель 
Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:
31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов.
Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины 
- если главный определитель системы отличен от нуля (
), то система имеет единственное решение;
- если главный определитель системы равен нулю (
), а хотя бы один из вспомогательных определителей отличен от нуля (
или
, или, . или
), то система не имеет решений (деление на нуль запрещено);
- если все определители системы равны нулю (
), то система имеет бесчисленное множество решений.
Пример:
Решить СЛАУ методом Крамера
Решение:
Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом
Найдем главный определитель СЛАУ (раскрываем по первой строке)
Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя
Воспользуемся формулами Крамера
Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений.
Выполним проверку 
Матричный способ решения СЛАУ
Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных 

Тогда СЛАУ можно записать в матричном виде 





Пример:
Решить СЛАУ матричным способом
Решение:
Введем в рассмотрение следующие матрицы
Найдем матрицу 
Пример:
Решение:
Найдем алгебраические дополнения всех элементов 


Отсюда находим, что х = 1; y = l; z = l.
Метод Гаусса
Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции. Расширенная матрица для СЛАУ имеет вид:
Замечание: В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы.
Обменяем в расширенной матрице первую и вторую строки местами, получим 

Умножим элементы первой строки на (—1) и прибавим к соответствующим элементам третьей строки 

Из первого уравнения находим, что х = 1.
Вывод: Из вышеизложенного материала следует, что вне зависимости от
способа решения СЛАУ всегда должен получаться один и тот же ответ.
Замечание: После нахождения решения СЛАУ надо обязательно выполнить проверку, то есть подставить полученные значения неизвестных в заданную СЛАУ и убедиться в тождественности левой части всех равенств системы соответствующим правым частям. Отметим, что задание СЛАУ всегда верно, то есть, если проверка показывает нарушение оговоренной тождественности, то надо искать ошибку в проведенных вычислениях.
Ранг матрицы. Теорема Кронекера-Капелли
Определение: Рангом матрицы 
Если 
При вычислении ранга необходимо начинать вычислять миноры 2 порядка, затем миноры 3 порядка и так далее, пока не будут найдены миноры, обращающиеся в нуль. Если все миноры порядка p равны нулю, то и все миноры, порядок которых больше p, равны нулю.
Пример:
Найти ранг матрицы
Решение:
Очевидно, что среди миноров второго порядка есть миноры отличные от нуля, например, 


Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах.
Следствия из теоремы Кронекера — Капелли
Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).
Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).
В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Экстремум функции
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Электронная библиотека
Прямоугольная таблица, составленная из mxn элементов aii (i = 1,2,3,…n; j = 1,2,3,…m) некоторого множества, называется матрицей размера mxn.
Матрицы обозначают большими латинскими буквами А, В… Например:
Элементы а11, а12,…, а1n образуют первую строку; а11, а21,…,аm1 – первый столбец. Строки и столбцы называют рядами. Произвольный элемент матрицы обозначают aij. Краткая форма записи матрицы: (aij)mn, а числа i, j называют индексами элемента. Элементы а11, a22, …,amn образуют главную диагональ матрицы. Если m = n, то матрица называется квадратной.
Матрица, состоящая из одной строки или одного столбца, соответственно называется матрицей-строкой или матрицей-столбцом.
Матрица, всё элементы которой равны нулю, называется нулевой и обозначается буквой О.
Порядком матрицы называется число её строк (для квадратной матрицы).
Квадратная матрица называется симметрической, если аij = aji.
Диагональной матрицей называется квадратная матрица, у которой все элементы не принадлежащей главной диагонали равны нулю, и обозначается символом:
Единичной называется диагональная матрица, все элементы главной диагонали которой равны единице, и обозначается Е или I:
Матрица, полученная из данной матрицы А заменой каждой её строки соответствующим столбцом, называется транспонированной и обозначается А Т .
Линейные операции над матрицами
К линейным операциям относятся: сложение и вычитание матриц, умножение матрицы на число. Сложение и вычитание определяется только для матриц одинаковых размеров.
Произведением матрицы А = (аij)mn на число называется матрица:
то есть каждый элемент матрицы А умножается на число .
Произведение определяется для квадратных матриц одного и того же порядка, а также для прямоугольных матриц, у которых число столбцов множимого равно числу строк матрицы множителя. Обозначается:
(элемент матрицы Сij равен сумме произведений элементов i-строки матрицы А на соответствующие элементы j-го столбца матрицы В). Заметим, что не всегда = .
Определители. Минор и алгебраическое дополнение
Определители вводятся для квадратных матриц.
Определителем квадратной матрицы второго порядка называется число, равное а11а22 — а12а21, обозначается символом:
Имеют место свойства определителей и теоремы, которые касаются их вычисления.
Определителем квадратной матрицы А = (аij)3x3 (третьего порядка) называют число:
Минором элемента aij определителя называется определитель, полученный из данного вычеркиванием той строки и того столбца, которым принадлежит данный элемент. Минор элемента aij обозначается Мij.
Алгебраическим дополнением элемента aij определителя называется его минор, взятый со знаком (-1) i+ j , обозначается символом Aij:
Для определителей вводится понятие порядка «по принципу порядка матрицы».
Если определитель имеет порядок выше трех, то пользуются для его вычисления важным для определителей свойством «разложения» определителя по строке или столбцу.
Определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.
Коротко можно записать так:
— разложение определителя по элементам i-й строки.
На практике часто используют теорему вычисления определителя от произведения матриц.
Она утверждает: определитель произведения двух квадратных матриц А и В одного порядка равен произведению определителей перемножаемых матриц:
Пример 14. Вычислить определитель по правилу «разложения»:
1) разложим определитель по элементам четвёртого столбца, который содержит три «нулевых» элемента, которые впоследствии умножаются на алгебраические дополнения (не важно, какие они имеют значения), и за счёт этого имеем выигрыш в вычислении всего определителя;
2) вычисляем алгебраическое дополнение А44 по правилу треугольника (заметим, что можно было и далее вычислять этот определитель 3-го порядка по правилу разложения, но в целях экономии времени пользуемся правилом, которое знаем для определителя 3-го порядка).
Определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.
Если система является невырожденной, т.е. , то она имеет единственное решение
где А -1 — матрица, обратная матрице А, а
Линейные системы уравнений
называется невырожденной, если . Тогда эта система имеет единственное решение:
Эти формулы называются формулами Крамера.
Из формул Крамера следует, что если однородная линейная система
имеет ненулевое решение, то её определитель det А = 0.
Решение однородной системы двух уравнений.
Пусть дана система:
Решения даются формулами:
где — алгебраические дополнения матрицы 3-го порядка, составленные из коэффициентов при неизвестных данной системы.
Решения однородной системы трех линейных уравнений:
если det А = 0, А33 , находятся из подсистемы по предыдущим формулам (см. предыдущий пункт).
Пример 15: Решить систему с помощью определителей:
Пример 16: Решить однородную систему:
http://www.evkova.org/metodyi-resheniya-sistem-linejnyih-algebraicheskih-uravnenij-slau
http://libraryno.ru/6-matricy-opredeliteli-lineynye-sistemy-uravneniy-sp_kostenko/






 .
. — нельзя, т.к. размеры матриц различны.
— нельзя, т.к. размеры матриц различны. .
.

 .
. .
. ,
,  .
.



 .
.
 .
. .
. .
.





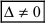 ), то система имеет единственное решение;
), то система имеет единственное решение;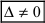 ), а хотя бы один из вспомогательных определителей отличен от нуля (
), а хотя бы один из вспомогательных определителей отличен от нуля ( 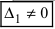 или
или 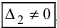 , или, . или
, или, . или 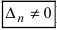 ), то система не имеет решений (деление на нуль запрещено);
), то система не имеет решений (деление на нуль запрещено);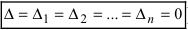 ), то система имеет бесчисленное множество решений.
), то система имеет бесчисленное множество решений.














