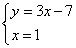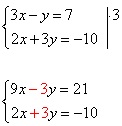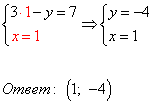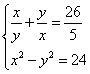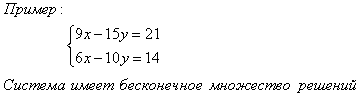Математика
Тестирование онлайн
Система линейных уравнений
Обычно уравнения системы записывают в столбик одно под другим и объединяют фигурной скобкой
Система уравнений такого вида, где a, b, c — числа, а x, y — переменные, называется системой линейных уравнений.
При решении системы уравнений используют свойства, справедливые для решения уравнений.
Решение системы линейных уравнений способом подстановки
Рассмотрим пример
1) Выразить в одном из уравнений переменную. Например, выразим y в первом уравнении, получим систему:
2) Подставляем во второе уравнение системы вместо y выражение 3х-7:
3) Решаем полученное второе уравнение:
4) Полученное решение подставляем в первое уравнение системы:
Система уравнений имеет единственное решение: пару чисел x=1, y=-4. Ответ: (1; -4), записывается в скобках, на первой позиции значение x, на второй — y.
Решение системы линейных уравнений способом сложения
Решим систему уравнений из предыдущего примера 
1) Преобразовать систему таким образом, чтобы коэффициенты при одной из переменных стали противоположными. Умножим первое уравнение системы на «3».
2) Складываем почленно уравнения системы. Второе уравнение системы (любое) переписываем без изменений.
3) Полученное решение подставляем в первое уравнение системы:
Решение системы линейных уравнений графическим способом
Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.
Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может: а) иметь единственное решение; б) не иметь решений; в) иметь бесконечное множество решений.
2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.
Графическое решение системы
Метод введения новых переменных
Замена переменных может привести к решению более простой системы уравнений, чем исходная.
Рассмотрим решение системы
Введем замену 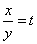
Переходим к первоначальным переменным
Особые случаи
Не решая системы линейных уравнений, можно определить число ее решений по коэффициентам при соответствующих переменных.
Пусть дана система
1) Если 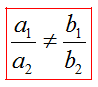
2) Если 
3) Если 
Метод Гаусса*
Суть метода в последовательном исключении неизвестных, приводя систему линейных уравнений к ступенчатой форме.
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Решение системы двух линейных уравнений с двумя переменными.
Метод подстановки и сложения.
С помощью данной математической программы вы можете решить систему двух линейных уравнений с двумя переменными методом подстановки и методом сложения.
Программа не только даёт ответ задачи, но и приводит подробное решение с пояснениями шагов решения двумя способами: методом подстановки и методом сложения.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
В качестве переменной может выступать любая латинсая буква.
Например: \( x, y, z, a, b, c, o, p, q \) и т.д.
При вводе уравнений можно использовать скобки. При этом уравнения сначала упрощаются. Уравнения после упрощений должны быть линейными, т.е. вида ax+by+c=0 с точностью порядка следования элементов.
Например: 6x+1 = 5(x+y)+2
В уравнениях можно использовать не только целые, но также и дробные числа в виде десятичных и обыкновенных дробей.
Правила ввода десятичных дробей.
Целая и дробная часть в десятичных дробях может разделяться как точкой так и запятой.
Например: 2.1n + 3,5m = 55
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &
Примеры.
-1&2/3y + 5/3x = 55
2.1p + 55 = -2/7(3,5p — 2&1/8q)
Решить систему уравнений
Немного теории.
Решение систем линейных уравнений. Способ подстановки
Последовательность действий при решении системы линейных уравнений способом подстановки:
1) выражают из какого-нибудь уравнения системы одну переменную через другую;
2) подставляют в другое уравнение системы вместо этой переменной полученное выражение;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.
Пример. Решим систему уравнений:
$$ \left\< \begin
Выразим из первого уравнения y через x: y = 7-3x. Подставив во второе уравнение вместо y выражение 7-Зx, получим систему:
$$ \left\< \begin
Нетрудно показать, что первая и вторая системы имеют одни и те же решения. Во второй системе второе уравнение содержит только одну переменную. Решим это уравнение:
$$ -5x+2(7-3x)=3 \Rightarrow -5x+14-6x=3 \Rightarrow -11x=-11 \Rightarrow x=1 $$
Подставив в равенство y=7-3x вместо x число 1, найдем соответствующее значение y:
$$ y=7-3 \cdot 1 \Rightarrow y=4 $$
Пара (1;4) — решение системы
Системы уравнений с двумя переменными, имеющие одни и те же решения, называются равносильными. Системы, не имеющие решений, также считают равносильными.
Решение систем линейных уравнений способом сложения
Рассмотрим еще один способ решения систем линейных уравнений — способ сложения. При решении систем этим способом, как и при решении способом подстановки, мы переходим от данной системы к другой, равносильной ей системе, в которой одно из уравнений содержит только одну переменную.
Последовательность действий при решении системы линейных уравнений способом сложения:
1) умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;
2) складывают почленно левые и правые части уравнений системы;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.
Пример. Решим систему уравнений:
$$ \left\< \begin
В уравнениях этой системы коэффициенты при y являются противоположными числами. Сложив почленно левые и правые части уравнений, получим уравнение с одной переменной 3x=33. Заменим одно из уравнений системы, например первое, уравнением 3x=33. Получим систему
$$ \left\< \begin
Из уравнения 3x=33 находим, что x=11. Подставив это значение x в уравнение \( x-3y=38 \) получим уравнение с переменной y: \( 11-3y=38 \). Решим это уравнение:
\( -3y=27 \Rightarrow y=-9 \)
Таким образом мы нашли решение системмы уравнений способом сложения: \( x=11; y=-9 \) или \( (11; -9) \)
Воспользовавшись тем, что в уравнениях системы коэффициенты при y являются противоположными числами, мы свели ее решение к решению равносильной системы (сумировав обе части каждого из уравнений исходной симтемы), в которой одно из уравнений содержит только одну переменную.
Системы уравнений
Система уравнений — это группа уравнений, в которых одни и те же неизвестные обозначают одни те же числа. Чтобы показать, что уравнения рассматриваются как система, слева от них ставится фигурная скобка:
 | x — 4y = 2 |
| 3x — 2y = 16 |
Решить систему уравнений — это значит, найти общие решения для всех уравнений системы или убедиться, что решения нет.
Чтобы решить систему уравнений, нужно исключить одно неизвестное, то есть из двух уравнений с двумя неизвестными составить одно уравнение с одним неизвестным. Исключить одно из неизвестных можно тремя способами: подстановкой, сравнением, сложением или вычитанием.
Способ подстановки
Чтобы решить систему уравнений способом подстановки, нужно в одном из уравнений выразить одно неизвестное через другое и результат подставить в другое уравнение, которое после этого будет содержать только одно неизвестное. Затем находим значение этого неизвестного и подставляем его в первое уравнение, после этого находим значение второго неизвестного.
Рассмотрим решение системы уравнений:
 | x — 4y = 2 |
| 3x — 2y = 16 |
Сначала найдём, чему равен x в первом уравнении. Для этого перенесём все члены уравнения, не содержащие неизвестное x, в правую часть:
Так как x, на основании определения системы уравнений, имеет такое же значение и во втором уравнении, то подставляем его значение во второе уравнение и получаем уравнение с одним неизвестным:
| 3x | — 2y = 16; |
| 3( 2 + 4y ) | — 2y = 16. |
Решаем полученное уравнение, чтобы найти, чему равен y. Как решать уравнения с одним неизвестным, вы можете посмотреть в соответствующей теме.
| 3(2 + 4y) — 2y = 16; |
| 6 + 12y — 2y = 16; |
| 6 + 10y = 16; |
| 10y = 16 — 6; |
| 10y = 10; |
| y = 10 : 10; |
| y = 1. |
Мы определили что y = 1. Теперь, для нахождения численного значения x, подставим значение y в преобразованное первое уравнение, где мы ранее нашли, какому выражению равен x:
x = 2 + 4y = 2 + 4 · 1 = 2 + 4 = 6.
Способ сравнения
Способ сравнения — это частный случай подстановки. Чтобы решить систему уравнений способом сравнения, нужно в обоих уравнениях найти, какому выражению будет равно одно и то же неизвестное и приравнять полученные выражения друг к другу. Получившееся в результате уравнение позволяет узнать значение одного неизвестного. С помощью этого значения затем вычисляется значение второго неизвестного.
Например, для решение системы:
 | x — 4y = 2 |
| 3x — 2y = 16 |
найдём в обоих уравнениях, чему равен y (можно сделать и наоборот — найти, чему равен x):
| x — 4y = 2 | 3x — 2y = 16 |
| -4y = 2 — x | -2y = 16 — 3x |
| y = (2 — x) : — 4 | y = (16 — 3x) : -2 |
Составляем из полученных выражений уравнение:
| 2 — x | = | 16 — 3x |
| -4 | -2 |
Решаем уравнение, чтобы узнать значение x:
| ||||||
| 2 — x = 32 — 6x | ||||||
| —x + 6x = 32 — 2 | ||||||
| 5x = 30 | ||||||
| x = 30 : 5 | ||||||
| x = 6 |
Теперь подставляем значение x в первое или второе уравнение системы и находим значение y:
| x — 4y = 2 | 3x — 2y = 16 |
| 6 — 4y = 2 | 3 · 6 — 2y = 16 |
| -4y = 2 — 6 | -2y = 16 — 18 |
| -4y = -4 | -2y = -2 |
| y = 1 | y = 1 |
Способ сложения или вычитания
Чтобы решить систему уравнений способом сложения, нужно составить из двух уравнений одно, сложив левые и правые части, при этом одно из неизвестных должно быть исключено из полученного уравнения. Неизвестное можно исключить, уравняв при нём коэффициенты в обоих уравнениях.
 | x — 4y = 2 |
| 3x — 2y = 16 |
Уравняем коэффициенты при неизвестном y, умножив все члены второго уравнения на -2:
 | x — 4y = 2 |
| -6x + 4y = -32 |
Теперь сложим по частям оба уравнения, чтобы получить уравнение с одним неизвестным:
| + | x — 4y = 2 |
| -6x + 4y = -32 | |
| -5x = -30 |
Находим значение x (x = 6). Теперь, подставив значение x в любое уравнение системы, найдём y = 1.
Если уравнять коэффициенты у x, то, для исключения этого неизвестного, нужно было бы вычесть одно уравнение из другого.
Уравняем коэффициенты при неизвестном x, умножив все члены первого уравнения на 3:
(x — 4y) · 3 = 2 · 3
 | 3x — 12y = 6 |
| 3x — 2y = 16 |
Теперь вычтем по частям второе уравнение из первого, чтобы получить уравнение с одним неизвестным:
| — | 3x — 12y = 6 |
| 3x — 2y = 16 | |
| -10y = -10 |
Находим значение y (y = 1). Теперь, подставив значение y в любое уравнение системы, найдём x = 6:
| 3x — 2y = 16 |
| 3x — 2 · 1 = 16 |
| 3x — 2 = 16 |
| 3x = 16 + 2 |
| 3x = 18 |
| x = 18 : 3 |
| x = 6 |
Для решения системы уравнений, рассмотренной выше, был использован способ сложения, который основан на следующем свойстве:
Любое уравнение системы можно заменить на уравнение, получаемое путём сложения (или вычитания) уравнений, входящих в систему. При этом получается система уравнений, имеющая те же решения, что и исходная.
http://www.math-solution.ru/math-task/sys-lin-eq
http://izamorfix.ru/matematika/algebra/sistema_uravn.html