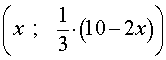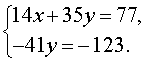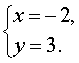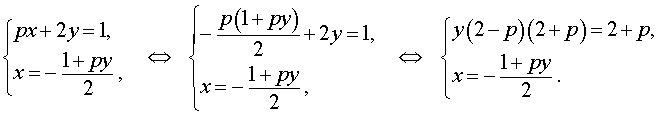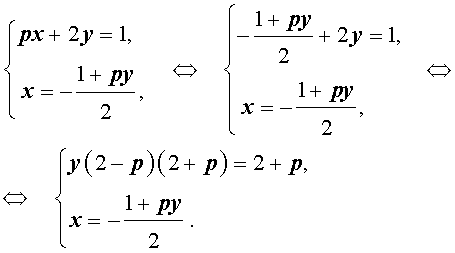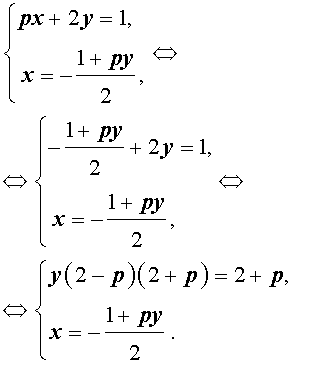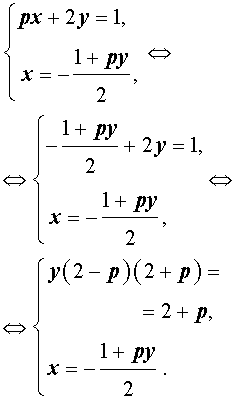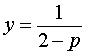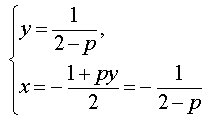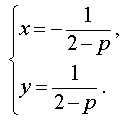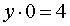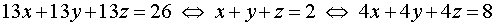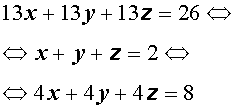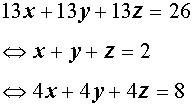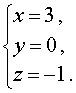Система уравнений первой степени примеры

Системы линейных уравнений

Линейные уравнения (уравнения первой степени) с двумя неизвестными

Системы из двух линейных уравнений с двумя неизвестными

Системы из трех линейных уравнений с тремя неизвестными

Линейные уравнения (уравнения первой степени) с двумя неизвестными

Определение 1 . Линейным уравнением (уравнением первой степени) с двумя неизвестными x и y называют уравнение, имеющее вид

ax +by = c ,

(1)

где a , b , c – заданные числа.

Определение 2 . Решением уравнения (1) называют пару чисел (x ; y) , для которых формула (1) является верным равенством.

Пример 1 . Найти решение уравнения

2x +3y = 10

(2)

Решение . Выразим из равенства (2) переменную y через переменную x :

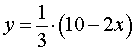(3)

Из формулы (3) следует, что решениями уравнения (2) служат все пары чисел вида

где x – любое число.

Замечание . Как видно из решения примера 1, уравнение (2) имеет бесконечно много решений. Однако важно отметить, что не любая пара чисел (x ; y) является решением этого уравнения. Для того, чтобы получить какое-нибудь решение уравнения (2), число x можно взять любым, а число y после этого вычислить по формуле (3).

Системы из двух линейных уравнений с двумя неизвестными

Определение 3 . Системой из двух линейных уравнений с двумя неизвестными x и y называют систему уравнений, имеющую вид

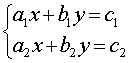(4)

Определение 4 . В системе уравнений (4) числа a₁ , b₁ , a₂ , b₂ называют коэффициентами при неизвестных , а числа c₁ , c₂ – свободными членами .

Определение 5 . Решением системы уравнений (4) называют пару чисел (x ; y) , являющуюся решением как одного, так и другого уравнения системы (4).

Определение 6 . Две системы уравнений называют равносильными (эквивалентными) , если все решения первой системы уравнений являются решениями второй системы, и все решения второй системы являются решениями первой системы.

Равносильность систем уравнений обозначают, используя символ «»

Системы линейных уравнений решают с помощью метода последовательного исключения неизвестных , который мы проиллюстрируем на примерах.

Пример 2 . Решить систему уравнений

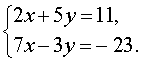(5)

Решение . Для того, чтобы решить систему (5) исключим из второго уравнения системы неизвестное х .

С этой целью сначала преобразуем систему (5) к виду, в котором коэффициенты при неизвестном x в первом и втором уравнениях системы станут одинаковыми.

Если первое уравнение системы (5) умножить на коэффициент, стоящий при x во втором уравнении (число 7 ), а второе уравнение умножить на коэффициент, стоящий при x в первом уравнении (число 2 ), то система (5) примет вид

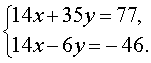(6)

Теперь совершим над системой (6) следующие преобразования:

первое уравнение системы оставим без изменений;
из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.

В результате система (6) преобразуется в равносильную ей систему

Из второго уравнения находим y = 3 , и, подставив это значение в первое уравнение, получаем

Пример 3 . Найти все значения параметра p , при которых система уравнений

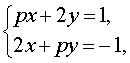(7)

а) имеет единственное решение;

б) имеет бесконечно много решений;

в) не имеет решений.

Решение . Выражая x через y из второго уравнения системы (7) и подставляя полученное выражение вместо x в первое уравнение системы (7), получим

Следовательно, система (7) равносильна системе

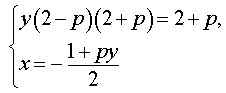(8)

Исследуем решения системы (8) в зависимости от значений параметра p . Для этого сначала рассмотрим первое уравнение системы (8):

y (2 – p) (2 + p) = 2 + p

(9)

Если , то уравнение (9) имеет единственное решение

Следовательно, система (8) равносильна системе

Таким образом, в случае, когда , система (7) имеет единственное решение

Если p = – 2 , то уравнение (9) принимает вид

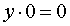
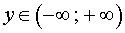
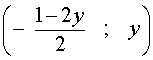
и его решением является любое число . Поэтому решением системы (7) служит бесконечное множество всех пар чисел

где y – любое число.

Если p = 2 , то уравнение (9) принимает вид

и решений не имеет, откуда вытекает, что и система (7) решений не имеет.

Системы из трех линейных уравнений с тремя неизвестными

Определение 7 . Системой из трех линейных уравнений с тремя неизвестными x , y и z называют систему уравнений, имеющую вид

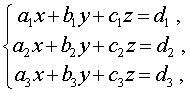(10)

Определение 9 . Решением системы уравнений (10) называют тройку чисел (x ; y ; z) , при подстановке которых в каждое из трех уравнений системы (10) получается верное равенство.

Пример 4 . Решить систему уравнений

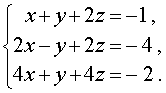(11)

Решение . Будем решать систему (11) при помощи метода последовательного исключения неизвестных .

Для этого сначала исключим из второго и третьего уравнений системы неизвестное y , совершив над системой (11) следующие преобразования:

первое уравнение системы оставим без изменений;
ко второму уравнению прибавим первое уравнение и заменим второе уравнение системы на полученную сумму;
из третьего уравнения вычтем первое уравнение и заменим третье уравнение системы на полученную разность.

В результате система (11) преобразуется в равносильную ей систему

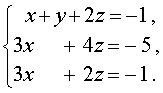(12)

Теперь исключим из третьего уравнения системы неизвестное x , совершив над системой (12) следующие преобразования:

первое и второе уравнения системы оставим без изменений;
из третьего уравнения вычтем второе уравнение и заменим третье уравнение системы на полученную разность.

В результате система (12) преобразуется в равносильную ей систему

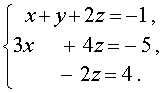(13)

Из системы (13) последовательно находим

Пример 5 . Решить систему уравнений

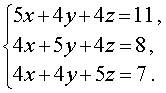(14)

Решение . Заметим, что из данной системы можно получить удобное следствие, сложив все три уравнения системы:

Если числа (x ; y ; z) являются решением системы (14), то они должны удовлетворять и уравнению (15). Однако в таком случае числа (x ; y ; z) должны также быть решением системы, которая получается, если из каждого уравнения системы (14) вычесть уравнение (15):

Поскольку мы использовали следствие из системы (14), не задумываясь о том, являются ли сделанные преобразования системы (14) равносильными, то полученный результат нужно проверить. Подставив тройку чисел (3 ; 0 ; –1) в исходную систему (14), убеждаемся, что числа (3 ; 0 ; –1) действительно являются ее решением.

Замечание . Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы с нелинейными уравнениями» и нашим учебным пособием «Системы уравнений».

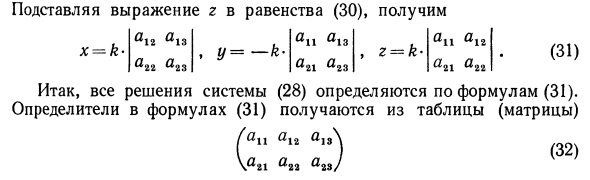
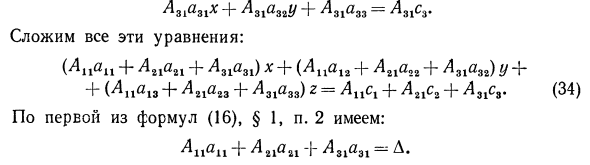
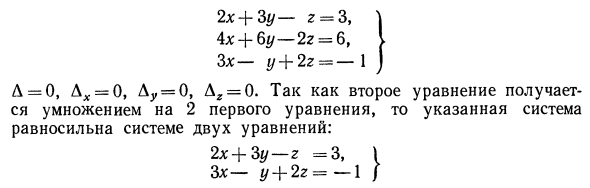
Системы уравнений первой степени

Система линейных уравнений Примените приведенную выше теорию определителей к решению системы линейных уравнений. (19) /. Система двух уравнений с двумя неизвестными Рассмотрим систему из двух уравнений первого порядка с двумя неизвестными хнами. a21x + a.guy = c2. / В обозначениях коэффициента aik первый индекс означает число уравнений, а второй индекс означает неизвестное число. Решите эту систему.

(Auait — ailavi) x = clatt — ctalt. (20) Точно так же, умножив первое уравнение на (-a21) на член и добавив, добавив второе, feAi-MiJ Y = sgap — saghh. (21) Однако на основе уравнения (2) (см. § 1, пункт I) его можно записать в виде: 2112 「P」 12 «21» 22 * s2ai-say1 = c \ arg ^ r «12 Вверх Cx a.s. CI c-z agg 11 22 Короче говоря, эти детерминанты показаны как: A = Вы есть с, а12 В деятельности Ах = (22) а21 а2т кр ^ 21 a.s. D- Определитель D (19), состоящий из неизвестных коэффициентов системы, называется определителем системы.

Для этого умножьте первое уравнение на π22, второе (–avl) на член и добавьте полученное уравнение. Людмила Фирмаль

Квалификатор DL. (Или Д ^) берется из определителя системы Д, если неизвестные x (или y) коэффициенты ai и a.p (или a12 и a.2.d) заменяются свободными членами cx и c2. С другой стороны, (22)у а? Согласно формуле коэффициента (18) § 1, пункт 2 равен нулю. Таким образом, уравнение (34) принимает вид: A • x = Aps1 + Aisg -f A3lcs. (31 ‘) Рассмотрим детерминанты s, «gg» 13 сг аг, г «23» C * «z *» 33 Если коэффициенты x (т. Е. An, a21, a31) заменить свободными членами clt cs, c3, они взяты из определителя системы D. Разлагает этот определитель на элементы первого столбца.

Обратите внимание, что в этом определителе алгебраические дополнения элементов c19, c3 соответствуют соответствующим алгебраическим дополнениям элементов ai, a21, a31 определителя D, A ps, + L21s2 -f Akhs. = Dx, (35) Сравнение (35) и (34 ‘) Dx = Dx. (36) Уравнение также оценивается D-y = Au и D-2 = Dg, (37) где Значение х может быть подтверждено путем прямой проверки. / г, г «А» 13 «11» 12 С, = «21» 23. A 、 — 「21」 22 3 », 33 31 » 32 Определители Au и Dt взяты из определителя системы A, где коэффициенты y и r заменены свободными членами. Предполагая, что определитель системы A = ^ 0, из уравнений (36) и (37),

Примеры решения и задачи с методическими указаниями

Решение задач	Лекции
Сборник и задачник	Учебник

Найти решение системы (33) в уравнении (38). Уравнение (38) называется уравнением Крамера, как и уравнение (25). Подобные уравнения применяются к линейным уравнениям со многими неизвестными. Пример 1. Решение системы Решение здесь 1 2-1 D = 2 -3 2 = -8, Dx = 3 1 1 12-1 2 2-1 2-3 2 = -8, 8 1 1 1 2 2 D = 2 2 2 = -16, Dg = 2 3 8 1 По формуле (38), -8 Если определитель системы Д = 0 и хотя бы один из определителей Дх, Ду, Дг не равен нулю, то система (33) не имеет решения (не совместимо). Конечно, предположим, что ясно, что хχ> 0. В этом случае уравнение (36) невозможно. Это потому, что Dx = 0 слева и Dx = ^ 0 справа для всех x.

Наконец, отметим, что если D = 0 и DX = D ^ = Dr = 0, система (33) не имеет решения или доказательства того, что существует бесконечно много решений. Это иллюстрируется примером. Пример 3. Рассмотрение системы x — (/ 4-2g = 2, 2x-2 # 4-4g = 4, 3x-3 * / + 6g = 3. Где Д = 0, Ax = 0, Ду = 0, Дг = 0. Например, система не имеет решения, потому что первое и третье уравнения этой системы противоречивы. Фактически, умножение первого уравнения на 3 и вычитание третьего уравнения приводит к невозможному уравнению 0 = 3. Пример 4: Система 2 —3 2 = —24. 3 1 8

2x + 3 * / -r = 3, \ 4x — \ — 6y — 2z = 6, I 3x-g / + 22 = -1 j Л = О, Лх = 0, Ду = 0, Ar = 0. Эта система эквивалентна системе двух уравнений, поскольку второе уравнение получается умножением 2 первого уравнения. 2x + 3y-r = 3, \ 3x-y + 2r = -1 j

Есть бесчисленное множество решений. Установите любое значение x, чтобы получить соответствующее значение y и r. Например, если x = \, получить систему 3 года -2 = 1, 1- £ / 4-22 = -4, / 2 11 Решение этой проблемы дает y = —j, r = —y. Когда x = 0, r / = 1 »r = 0 и т. Д. 4. Однородная система первых трех уравнений 3 неизвестных Однородная система, состоящая из трех уравнений первого порядка с тремя неизвестными тревога + al2y + al3z = 0, \ a2lx + a22y + a23z = 0, I (39) a31x + azgu + a33g = 0 Дж В этом случае каждый определитель имеет столбец, и все его члены равны нулю, поэтому Ax = Ay = Az = 0. Уравнения (36) и (37) с. 3

принимает следующую форму: A-x = 0, D.0 = 0, D-g = 0. (40) Для системы (39) и определителя Φ0 система (39) имеет единственное решение x-y-r = 0. Чтобы система (39) имела ненулевое решение, требуется A = 0. Фактически, если x = £ 0, например, A = 0 из первого уравнения в (40). Следовательно, если решение однородной системы (39) не равно нулю, ее определитель равен A = 0. Наоборот, если ∆ = 0, система (39) всегда имеет ненулевое решение. Мы не предоставляем доказательств этого утверждения.

Уравнения (20) и (21) можно записать в следующем виде: Ax = Ax, A * Y = Au. Здесь есть два случая. I. Детерминанты системы = = = = 0. Затем разделите обе части каждого уравнения (23) на D, чтобы получить (24) В L * Или в развернутом виде «12 C * 2 fl «22 «11» 12 я «21» 22 1 Y = «P C1 а21 с2 (25) «II» 12 Уравнение (24) (или 25), называемое уравнением Крамера *, дает решение системы (19). (Рекомендуется проверить это.) Таким образом, если определитель D системы (19) не равен нулю, система имеет единственное решение, определяемое уравнением (24) или (25). II. Определителем системы является A = axla22 — a2lal2-0t, т.е. ahha.r2 = = 212112. В этом случае неизвестный коэффициент одного уравнения пропорционален неизвестному коэффициенту другого уравнения. На самом деле, предположим, что один из них, например ax x 0, обозначен как — = откуда atl = A, au. следующий «И Если ahx22 = a2Xa12, вы можете видеть, что a22 = HaX2.

Учитывая это, система (19) может быть описана как: (26) aixx + ax2y = cx, b (a1Xx + aX2y) = c2. Я Есть два случая. 1) Определители как Ax, так и D, равные нулю: Ax = cx22 — cxaX2 = 0, Au = cmxx — cxai = 0. В этом случае числа a21, a22 и c2 пропорциональны числам, и aX2, c19 и system (19) могут быть записаны в следующем формате: 1 (27) Следовательно, второе уравнение системы берется из первого уравнения путем умножения обеих частей на X. То есть результат первого уравнения. В этом случае очевидно, что в системе (19) существует бесчисленное множество решений. Например, установив произвольное значение //, получается соответствующее значение x = Cl

2) хотя бы один из определителей Ax или Au не равен нулю. Например, предположим, что Au = ais2-a21cxΦ0. a11c2Fa21c1 и, следовательно, c2F \ cx. В этом случае, как видно из (26), второе уравнение ((ццХ + alty) = c2 не согласуется с первым уравнением, поэтому в системе (19) нет решения (или они говорят Не совместимо). Давайте посмотрим на некоторые примеры. Пример 1. Решение системы 2 * + 3 «/ = 7D 4x — 5 * / = 2. / Решения. здесь 2 3 4 —5 3 5 2 7 4 2 D = —22, = -41, D «= = –24.

Поскольку это определитель системы, он уникален для системы Решение определяется по уравнению (24): Ах 41 А. х = — _ U-12 U

L 22 11 22 Геометрически это линия, определяемая уравнением (41 12 \ 22 * IT J (CM * GL * § 1, раздел 5). Пример 2. Решение системы Решения. Здесь 2 5 = 0, D = 4 10 2x — \ — 5y = 3, я 4x + \ 0y-6./ 3 5 _ | 2 3 4 6 = 0, = 0 6 10 Второе выражение получается с начала путем умножения обеих сторон первого выражения на K = 2. Следовательно, система эквивалентна одной формуле 2x + 5r / = 3 и имеет бесконечное число решений. Если вы дадите произвольное значение неизвестному y, вы найдете x = 3-5f /. s Например, если * / = 0, * = -2, если = 1, d =, если x-1. Геометрически это означает, что уравнения соответствуют одной и той же прямой. И 4х + 10 2 «12» 13 я «22» 23 1 «А» 12 я «21» 22 1 G, у = «А» 12 «21» 22 Ах ах «21» 22 „_ 1″ 21-av £ | «11» 121 1 «21» 22 I Используя свойство определителя (см. § 1, подраздел 1), — «132» 12 = _z «13» 12 = Z «12» 13 f «11-» 13 * = -r

«23 *» 22 «23» 22 «22» 23 «21-» 23 * «21» 23 так А 13 13 21 23 «11» 12 «21» 22 = / e, то z = k шоу «11» 12 «21» 22 (28) φ0, (29) Ах ах

Подстановка уравнения r в уравнение (30) дает: «12 а1Я а2т а23 「11」 13 «21» 23 «11» 12 «21» 22 х = к- г-к- (31) , * / = -K- Следовательно, все решения системы (28) определяются уравнением (31). Определитель уравнения (31) получается из таблицы (матрицы). «11» 12 «13 v» 21 «22» 23 /Получите различные тройки x, y, r, которые являются решением системы, удалив соответствующие столбцы один за другим и присвоив коэффициенту k разные числа (28). Пример. Решить систему 2x + 3

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Уравнения и системы уравнений первой степени

Главная > Решение

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

Уравнения и системы уравнений первой степени

Два числа или какие-нибудь выражения, соединенные знаком « = », образуют равенство . Если данные числа или выражения при любых значениях букв равны, то такое равенство называют тождеством .

Например, когда утверждают, что при любом а действительном:

а + 1 = 1 + а , здесь равенство является тождеством.

Уравнением называется равенство, содержащее неизвестные числа, обозначенные буквами. Эти буквы называют неизвестными . Неизвестных в уравнении может быть несколько.

Например, в уравнении 2 х + у = 7 х – 3 два неизвестных: х и у .

Выражение, стоящее в уравнении слева (2 х + у ) называют левой частью уравнения, а выражение, стоящее в уравнении справа (7 х – 3), называют правой его частью.

Значение неизвестного, при котором уравнение становится тождеством, называется решением или корнем уравнения.

Например, если в уравнение 3 х + 7=13 вместо неизвестного х подставить число 2, получим тождество . Следовательно, значение х = 2 удовлетворяет данному уравнению и число 2 есть решение или корень данного уравнения.

Два уравнения называются равносильными (или эквивалентными ), если все решения первого уравнения являются решениями второго и наоборот, все решения второго уравнения являются решениями первого. К равносильным уравнениям относятся также уравнения, не имеющие решений.

Например, уравнения 2 х – 5 = 11 и 7 х + 6 = 62 равносильны, так как они имеют один и тот же корень х = 8; уравнения х + 2 = х + 5 и 2 х + 7 = 2 х равносильны, потому что оба не имеют решений.

Свойства равносильных уравнений

К обеим частям уравнения можно прибавить любое выражение, имеющее смысл при всех допустимых значениях неизвестного; полученное уравнение будет равносильно данному.

Пример. Уравнение 2 х – 1 = 7 имеет корень х = 4. Прибавив к обеим частям по 5, получим уравнение 2 х – 1 + 5 = 7 + 5 или 2 х + 4 = 12, которое имеет тот же корень х = 4.

2. Если в обеих частях уравнения имеются одинаковые члены, то их можно опустить.

Пример. Уравнение 9 х + 5 х = 18 + 5 х имеет один корень х = 2. Опустив в обеих частях 5 х , получим уравнение 9 х = 18, которое имеет тот же корень х = 2.

3. Любой член уравнения можно перенести из одной части уравнения в другую, изменив его знак на противоположный.

Пример. Уравнение 7 х — 11 = 3 имеет один корень х = 2. Если перенести 11 в правую часть с противоположным знаком, получим уравнение 7 х = 3 + 11, которое имеет то же решение х = 2.

4. Обе части уравнения можно умножить на любое выражение (число), имеющее смысл и отличное от нуля при всех допустимых значениях неизвестного, полученное уравнение будет равносильно данному.

Пример. Уравнение 2 х — 15 = 10 – 3 х имеет корень х = 5. Умножив обе части на 3, получим уравнение 3(2 х – 15) = 3(10 – 3 х ) или 6 х – 45 =30 – 9 х , которое имеет тот же корень х = 5.

5. Знаки всех членов уравнения можно изменить на противоположные (это равносильно умножению обеих частей на (-1)).

Пример. Уравнение – 3 х + 7 = – 8 после умножения обеих частей на (-1) примет вид 3 х — 7 = 8. Первое и второе уравнения имеют единственный корень х = 5.

6. Обе части уравнения можно разделить на одно и тоже число, отличное от нуля (то есть, не равное нулю).

Пример. Уравнение имеет два корня: и . Разделив все его члены на 3, получим уравнение , равносильное данному, так как оно имеет те же два корня: и .

7. Уравнение, в котором коэффициенты всех или нескольких членов дробные числа, можно заменить равносильным ему уравнением с целыми коэффициентами, для этого обе части уравнения надо умножить на наименьшее общее кратное знаменателей дробных коэффициентов.

Пример. Уравнение после умножения обеих частей на 14 примет вид:

. Легко убедиться в том, что первое и последнее уравнения имеют корень х = 10.

Уравнения первой степени

Уравнение с одним неизвестным, которое после раскрытия скобок и приведения подобных членов принимает вид , где произвольные числа, х – неизвестное, называется уравнением первой степени с одним неизвестным (или линейным уравнением с одним неизвестным).

Пример. 2 х + 3 = 7 – 0,5 х ; 0,3 х = 0.

Уравнение первой степени с одним неизвестным всегда имеет одно решение; линейное уравнение может не иметь решений () или иметь их бесконечное множество ().

Пример. Решить уравнение .

Решение. Умножим все члены уравнения на наименьшее общее кратное знаменателей, равное 12.

После сокращения получим: . Раскроем скобки, чтобы отделить члены, содержащие неизвестное и свободные члены:

Сгруппируем в одной части (левой) члены, содержащие неизвестное, а в другой части (правой) — свободные члены:

. Приведем подобные члены: . Разделив обе части на (-22), получим х = 7.

Системы двух уравнений первой степени с двумя неизвестными

Уравнение вида , где называется уравнением первой степени с двумя неизвестными х и у . Если находят общие решения двух и более уравнений то говорят, что эти уравнения образуют систему, их записывают обычно одно под другим и объединяют фигурной скобкой, например .

Каждая пара значений неизвестных, которая одновременно удовлетворяет обоим уравнениям системы, называется решением системы . Решить систему – это значит найти все решения этой системы или показать, что она их не имеет. Две системы уравнений называются равносильными ( эквивалентными ), если все решения одной из них являются решениями другой и наоборот, все решения другой являются решениями первой.

Например, решением системы является пара чисел х = 4 и у = 3. Эти числа являются также единственным решением системы . Следовательно, эти системы уравнений равносильны.

Способы решения систем уравнений

1. Способ алгебраического сложения. Если коэффициенты при каком-нибудь неизвестном в обоих уравнениях равны по абсолютной величине, то складывая оба уравнения (или вычитая одно из другого), можно получить уравнение с одним неизвестным. Решая это уравнение, определяют одно неизвестное, а подставляя его в одно из уравнений системы, находят второе неизвестное.

Примеры: Решить системы уравнений: 1) .

Здесь коэффициенты при у по абсолютной величине равны между собой, но противоположны по знаку. Для получения уравнения с одним неизвестным уравнения системы почленно складываем:

Полученное значение х = 4 подставляем в какое-нибудь уравнение системы, например в первое, и находим значение у : .

Ответ: х = 4; у = 3.

2) .

Уравняем коэффициенты при х . Для этого умножим первое уравнение на 3, а второе на (– 2) и сложим полученные уравнения.

Ответ: .

2. Способ подстановки. Из любого уравнения системы одну из неизестных выражаем через остальные, а затем подставляем значение этой неизвестной в остальные уравнения. Рассмотрим этот способ на конкретных примерах:

1) Решим систему уравнений . Выразим из первого уравнения одно из неизвестных, например х : и подставим полученное значение х во второе уравнение системы, получим уравнение с одним неизвестным у :

Подставим у = 1 в выражение для х , получим .

Ответ: .

2) . В этом случае удобно выразить у из второго уравнения:

. Полученное значение у подставляем в первое уравнение и получаем уравнение с одним неизвестным х :

Подставим значение х = 5 в выражение для у , получим .

Ответ: .

3) Решим систему уравнений . Из первого уравнения находим . Подставив это значение во второе уравнение, получим уравнение с одним неизвестным у :

Подставим у = 5 в выражение для х , получим

Ответ: .

3. Способ замены. К cистемам двух линейных уравнений с двумя неизвестными можно приводить некоторые нелинейные системы. Это можно осуществлять способом замены.

Пример. Решить систему. .

Перепишем систему в виде: . Заменим неизвестные, положив , получим линейную систему . Из первого уравнения выразим неизвестное . Подставим значение во второе уравнение, получим уравнение с одним неизвестным: