Указания и задания для контрольной работы по учебной дисциплине «Математика» для специальности: 080110-«Экономика и бухгалтерский учет»
Для того, чтобы облегчить студенту-заочнику самостоятельное выполнение контрольных работ, приведем примеры решений задач, аналогичных тем, какие предлагаются в контрольных работах. Подобные задачи включаются и в экзаменационные билеты.
Раздел I. Линейная алгебра
Задача 1. Дана система линейных уравнений
Требуется показать, что система совместна, и найти ее решение тремя способами: а) по формулам Крамера; б) методом Гаусса; в) методом обратной матрицы. Выполнить проверку решения.
Система n линейных уравнений с n неизвестными является совместной и имеет единственное решение, так как определитель системы, составленный из коэффициентов при неизвестных не равен нулю. Вычислим определитель системы методом разложения его по элементом строки. Разложим по первой строке:
Так как определитель системы не равен нулю, система уравнений совместна и имеет единственное решение.
а) Найдем решение системы по формулам Крамера



где D1 D2 D3 — определители, которые получаются из определителя D системы путем замены в нем соответственно 1-го, 2-го, 3-го столбцов коэффициентов при неизвестных x1 x2 x3 столбцом свободных членов уравнений, стоящих в правой части данной системы. Получим следующие три определителя:
Вычислить неизвестные 


Проверим это решение, подставив значения неизвестных во все уравнения системы. Получим 
б) Решим ту же систему уравнений методом Гаусса. Для этого выпишем расширенную матрицу системы и приведем основную матрицу системы к треугольному виду или ступенчатому виду, если число уравнений окажется меньшим числа неизвестных. Приведение матрицы к треугольному виду, то есть такому, когда ниже (или выше) главной диагонали все элементы будут нулевые, а на главной диагонали — ненулевые, всегда возможно. Оно основано на следующих элементарных преобразованиях матрицы, соответствующих эквивалентным преобразованиям система:
1. Перестановка строк матрицы;
2. Перестановка столбцов;
3. Умножение всех элементов строки на одно и то же число;
4. Сложение элементов любой строки с соответствующими элементами любой другой строки;
5. Вычеркивание получившихся нулевых строк.
Вот решение одной системы методом последовательных исключений неизвестных:
Расширенная матрица 1-й шаг 2-шаг
Возвратимся теперь от матричной записи к системе уравнений. Из последней строки матрицы следует уравнение 




Существует модифицированный метод Гаусса, так называемый метод полного исключения неизвестных, в результате которого основная матрица системы преобразуется в каноническую матрицу, на главной диагонали которой остаются единицы, а все остальные элементы обращаются в нули. Таким образом сразу получается решение.
В основе этого метода лежит следующий алгоритм (строго определенный порядок действий)
1. Выберем разрешающую строку и в ней разрешающий элемент. Обычно это первый элемент первой строки, считая слева направо. Строки можно целиком переставлять, так что на первое место можно записать любую строку, в которой первый элемент не равен нулю.
2. Каждый элемент, разрешающий строки разделим на разрешающий элемент.
3. Элементы разрешающего столбца заменим нулями во всех строках матрицы, кроме разрешающей, где он буден равен единице.
4. Элементы столбцов, Которые были разрешающими на предыдущих шагах исключения, переписываем без изменения.
5. Остальные элементы пересчитаем по следующему правилу «прямоугольника»:


Где П – пересчитываемый элемент, Р – Разрешающий, D1 и D2 – “диагональные”, И – искомый. Все эти элементы каждый раз должны быть вершинами воображаемого прямоугольника, образованного параллельными строками и столбцами. Искомый элемент записываем на месте пересчитываемого.
Вернемся к расширенной матрице данной системы и выполним эквивалентной преобразования по предложенной выше схеме полного исключения неизвестных. Рекомендуем читателю все пересчеты коэффициентов по правилу «четырехугольника» записывать подробно.
Данная расширенная матрица 1-й шаг 2-й шаг
3 — й шаг 4 – й шаг
Если в последней матрице вернуться к записи уравнений, то получим



Замечания: 1. Кружками обведены разрешающие элементы.
2. При переходе от 2-го шага к 3-му третью строку почленно разделили на 90/7.
в) Решить данную систему методом обратной матрицы.
Решение. Данную систему можно записать в матричном виде АХ = В,
где 

Решение матричного уравнения имеет вид Х = А-1 В = N, где А-1 – матрица, обратная матрицы А. Так как определитель матрицы системы D(A) = 180 отличен от нуля то матрица А имеет обратную. Для вычисления обратной матрицы воспользуемся формулой
Где А11, А12, …, А33 – алгебраические дополнения элементов а11, а12, …, а33 матрицы А. Вычислим алгебраические дополнения всех элементов матрицы А:








Составим обратную матрицу

Найдем теперь матрицу Х.
Из равенства матриц Х = N или 
х1=2, х2 = 1, х3 = -3.
Задача 2. Даны матрицы 

произведение матриц АВ.
Эти матрицы являются соответственными, так как число столбцов первой матрицы равно числу строк второй: их размеры 


Раздел II. Линейное программирование.
Тема: Решение ЗЛП, используя симплекс — метод.
Реальные задачи линейного программирования содержат, как правило, большое число ограничений и неизвестных.
Естественно, что решение таких задач связано с большим объемом вычислений и проводится на быстродействующих вычислительных машинах.
Алгоритм, лежащий в основе машинной программы, может быть связан со спецификой данного класса задач. Так, например, для решения транспортной задачи имеются весьма простые алгоритмы, обусловленные особенностями ее системы ограничений.
Однако существуют и общие методы, позволяющие найти решение любой задачи линейного программирования за конечное число шагов. К их числу относится, прежде всего, так называемый симплекс-метод.
Для применения симплекс – метода к решению задачи линейного программирования требуется ее представление в каноническом, допустимом виде.
Пусть дана система m линейных уравнений с n неизвестными и линейная функция f.
Среди неотрицательных решений системы нужно найти такое, которой минимизирует функцию.
 |
Система уравнений приведена к допустимому виду, если
1. Какие-то неизвестные выражены через остальные неизвестные.
2. Свободные члены уравнений должны быть неотрицательными.
Неизвестные в допустимом виде системы, которые выражены через остальные, называются базисными, а весь набор этих неизвестных — допустимым базисом неизвестных (обозначим для краткости одной буквой Б).
Остальные неизвестные называются небазисными или свободными.
Весь процесс решения задачи линейного программирования симплексным методом можно записать в виде последовательности однотипно заполняемых таблиц, причем каждой итерации будет отвечать переход к следующей таблице.
Алгоритм решения ЗЛП по симплекс-методу:
1. Выделить исходный допустимый базис и заполнить первую таблицу.
2. Если в последней строке, не считая свободного члена, все элементы отрицательные, то минимум найден.
Минимальное значение функции равно свободному члену в строке целевой функции, а оптимальное решение определяется свободными членами при базисных переменных.
Все свободные переменные в этом случае равны нулю.
3. В последней строке симплекс-таблицы найти наименьший положительный элемент, не считая свободного члена.
Столбец, соответствующий этому элементу называется разрешающим.
4. Если в разрешающем столбце все элементы отрицательные, то задача не имеет решения, (минимум не достигается).
5. Вычислить отношение свободных членов к положительным элементам разрешающего столбца (симплекс-отношение).
Найти наименьшее из этих симплекс-отношений, оно соответствует разрешающей строке.
6. На пересечении разрешающего столбца и разрешающей строки найти разрешающий элемент.
7. Если имеется несколько одинаковых по величине симплекс-отношений, то выбирают любое из них.
То же самое относится к положительным элементам последней строки симплекс-таблицы.
8. После нахождения разрешающего элемента перейти к следующей таблице.
Заменить переменную, соответствующую разрешающей строке на переменную соответствующую разрешающему столбцу. При этом базисная переменная становится свободной переменной и наоборот.
9. Все элементы разрешающей строки разделить на разрешающий элемент.
10. Все элементы разрешающего столбца, кроме разрешающего элемента заменить 0.
11. Все остальные элементы таблицы рассчитать по правилу прямоугольника.
Правило прямоугольника: Для получения любого элемента новой симплекс-таблицы надо из соответствующего элемента новой таблицы вычесть произведение элемента разрешающей строки на элемент разрешающего столбца, разделенного на разрешающий элемент.
12. Продолжить выполнение алгоритма с пункта №2.
1. Приведем ЗЛП к каноническому виду.
Введем балансовые переменные x3, x4, x5.
2. Выделим допустимый базис.

Замечаем, что переменные x3, x4, x5 удовлетворяют условию допустимости, так как каждая из них входит только в одно уравнение, и, при этом, свободные члены неотрицательные.
Преобразуем целевую функцию.
3. Составляем симплекс-таблицы.
Элементарные преобразования системы линейных уравнений.
Алгебра и теория чисел
Лекция 3
Системы линейных уравнений
План
1. Основные понятия и обозначения.
2. Элементарные преобразования системы линейных уравнений.
3. Ступенчатая матрица. Приведение матрицы к ступенчатому виду.
Литература
1. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. 1997, с. 25-48.
2. Ермаков В.И. Общий курс высшей математики. М.: Инфра — М, 2000. с. 5-22
3. Кремер Н.Ш. Высшая математика для экономистов. М.: Юнити, 2000. с. 38-56.
1. Основные понятия и обозначения. Простейшие системы двух линейных уравнений с двумя неизвестными изучаются в средней школе:

Известно, что справедлив один из следующих трех случаев: либо система имет одно решение, либо имеет бесконечно много решений, либо не имеет решений. В этом параграфе мы будем рассматривать общие системы линейных уравнений и установим это утверждение в общем случае кроме того изложим один из наиболее удобных методов решения систем линейных уравнений — метод последовательного исключения неизвестных или метод Гаусса по имени выдающегося немецкого математика К. Ф. Гаусса (1777-1855).
Определение 1.Системой m линейных уравнений с n неизвестными

где a11 ,a12 . amn — фиксированные числа (действительные, комплексные или принадлежащие некоторому полю) , называемые коэффициентами при неизвестных, b1 ,b2 . bm — фиксированные числа, называемые свободными членами.
Если все свободные члены в системе линейных уравнений равны нулю, то система линейных уравнений называется однородной.
Определение 2.Решением системы линейных уравнений (1) называется такой упорядоченный набор n чисел 
Система называется совместной, если она имеет хотя бы одно решение, и называется несовместной, если она не имеет решений. Совместная система называется определенной, если она имеет одно решение, и называется неопределенной, если она не имеет решений.
Пусть S1 , S2 системы линейных уравнений с одним и тем же числом неизвестных, X1 , X2 — множества их решений соответственно.
Определение 3.Говорят, что система линейных уравнений S2 следствие системы S1 и S2 , если каждое решение системы S1 является решением системы S2 ,т.е. 

Определение 4. Говорят, что системы S1 и S2 равносильны, если каждое решение системы S1 является решением системы S2 и каждое решение системы S2 является решением системы S1 , т.е. 

Отношение следования и равносильности обладают следующими свойствами.
1. Если 


Действительно, если 

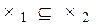



2. 
3. Если 

4. Если 
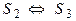
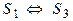
Свойства 2, 3, 4 доказываются аналогично.
Элементарные преобразования системы линейных уравнений.
Определение 5. Элементарными преобразованиями системы линейных уравнений называются ее следующие преобразования:
1) перестановка любых двух уравнений местами;
2) умножение обеих частей одного уравнения на любое число 
3) прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число k ;
(при этом все остальные уравнения остаются неизменными).
Нулевым уравнением называем уравнение следующего вида:

Теорема 1. Любая конечная последовательность элементарных преобразований и преобразование вычеркивание нулевого уравнения переводит одну систему линейных уравнений в равносильную ей другую систему линейных уравнений.
Доказательство.В силу свойства 4 предыдущего пункта достаточно доказать теорему для каждого преобразования отдельно.
1. При перестановке уравнений в системе местами сами уравнения неизменяются, поэтому по определению полученная система равносильная первоначальной .
2. В силу первой части доказательства достаточно доказать утверждение для первого уравнения. Умножим первое уравнение системы (1) на число 

Пусть 






Умножая его на число k,получим верное числовое равенство:

т.о. устанавливаем, что 
Обратно, если 





Отсюда по определению 4 система (1) равносильна системе (2).
3. В силу первой части доказательства достаточно доказать утверждение для первого и второго уравнения системы . Прибавим к обеим частям первому уравнению системы соответствующие части второго умноженные на число k , получим систему

Пусть 




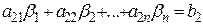
Прибавляя почленно к первому равенству второе, умноженное на число k получим верное числовое равенство:

Обратно, если 



Отсюда по определению 4 система (1) равносильна системе (5).
4. Так как нулевому уравнению удовлетворяет любой упорядоченный набор из n чисел, то при вычеркивании нулевого уравнения в системе получим систему равносильную исходной.
Ступенчатая матрица.
Определение 6.Матрицей размерности 
содержащая mn чисел, расположенных в m строк и n столбцов, числа 

Определение 7. Матрицей ступенчатого вида называется такая матрица, которая обладает свойствами:
1) в каждой строке матрицы имеется неравный нулю элемент;
2) в каждой строке матрицы, начиная со второй, первый слева неравный нулю элемент расположен правее первого слева неравного нулю элемента предыдущей строки матрицы.
Матрицу ступенчатого вида называют также трапециидальной матрицей, а квадратную матрицу ступенчатого вида называют треугольной матрицей. Ниже показаны две не ступенчатые матрицы и три ступенчатые матрицы (последняя матрица треугольная).







Определение 8. Элементарными преобразованиями строк матрицы называются следующие ее преобразования:
1) перестановка любых двух строк матрицы местами;
2) умножение одной строки матрицы на любое число 
3) прибавление к одной строке матрицы другой ее строки умноженной на любое число k ;
(при этом все остальные строки матрицы остаются неизменными).
Аналогично можно рассматривать элементарные преобразования столбцов матрицы.
Теорема 2. Любую ненулевую матрицу конечным числом элементарных преобразований и преобразований вычеркивания нулевой строки можно привести к матрице ступенчатого вида.
Доказательство.Доказательство проводим методом математической индукции по числу m строк матрицы. Для m=1 утверждение теоремы справедливо, так как ненулевая однострочная матрица по определению имеет ступенчатый вид.
Предположим, что утверждение теоремы доказано для матриц, имеющих m-1 строку и докажем его для матриц, в которых содержится m строк. Пусть первый слева отличный от нуля столбец данной матрицы имеет номер k , так как матрица ненулевая, то такой столбец найдется, и матрица имеет вид:
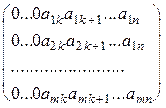
Можем считать, что элемент 




Рассмотрим матрицу, состоящую из последних m-1 строк матрицы (9):

Если матрица (10) нулевая, то все строки в матрице (9) кроме первой нулевые. Вычеркивая их, приходим к матрице ступенчатого вида. Если матрица (10) ненулевая, то по индуктивному предположению конечным число элементарных преобразований и преобразований вычеркивания нулевой строки может быть приведена к матрице ступенчатого вида: 
где элементы 



элементы 


4. Метод Гаусса. Системе линейных уравнений (1) соответствуют три матриц



Первая матрица называется матрицей системы, вторая — расширенной или присойдиненной матрицей системы, третья — столбцом свободных членов.
Система линейных уравнений называется системой ступенчатого вида, если расширенная матрица системы есть матрица ступенчатого вида. Неизвестные с коэффициентами неравными нулю, которые стоят первыми в уравнениях системы ступенчатого вида называются главными неизвестными, а остальные неизвестные называются свободными.
Линейное уравнение, в котором все коэффициенты равны нулю, а свободный член не равен нулю, т.е. уравнение вида:

не имеет решений. Действительно, если 

Пусть не все уравнения системы (1) нулевые. Тогда и расширенная матрица системы (1) ненулевая. По теореме 2 ее можно конечным числом элементарных преобразований и преобразований выбрасывания нулевой строки можно привести к матрице ступенчатого вида. Полученной матрице соответствует система линейных уравнений ступенчатого вида. Этим преобразованиям расширенной матрицы системы (1) соответствуют такие же преобразования системы линейных уравнений (1). По теореме 1 они переводят систему (1) в равносильную систему линейных уравнений, которая будет являются системой ступенчатого вида.
Таким образом мы доказали первую часть следующей теоремы.
Теорема 3.Любую систему линейных уравнений , содержащую ненулевое уравнение конечным числом элементарных преобразований и преобразований вычеркивания нулевого уравнения можно привести к равносильной ей системе ступенчатого вида. При этом возможны следующие три случая.
1. Если в полученной системе линейных уравнений ступенчатого вида есть противоречивое уравнение, то данная система не имеет решений.
2. Если в полученной системе линейных уравнений ступенчатого вида нет противоречивого уравнения и число уравнений в полученной системе равно числу неизвестных, то данная система имеет единственное решение.
3. Если в полученной системе линейных уравнений ступенчатого вида нет противоречивого уравнения и число уравнений в полученной системе меньше числа неизвестных, то данная система имеет бесконечно много решение.
Доказательство.Пусть дана система (1), содержащая ненулевое уравнение. По выше доказанному, она конечным числом элементарных преобразований она может быть преобразована к равносильной ей системе уравнений ступенчатого вида. Возможны случаи.
В полученной системе ступенчатого вида есть противоречивое уравнение. Тогда ни один набор чисел 
В полученной системе ступенчатого вида нет противоречивого уравнения. Тогда в каждом из уравнений системы ступенчатого вида содержится главное неизвестное. Отсюда получаем, что число главных неизвестных, а тем более число всех неизвестных, не менее числа уравнений в системе ступенчатого вида. Тогда возможны под случаи:
В системе ступенчатого вида число уравнений равно числу неизвестных, т. е. система имеет вид:

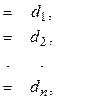
где 


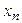




В системе ступенчатого вида число уравнений меньше числа неизвестных. В этом случае матрица полученной системы имеет вид (11), а
систему можно записать в виде:




где 




Следствие.Если в системе однородных уравнений число неизвестных больше числа уравнений, то система имеет бесконечно много решений.
Действительно, система однородных уравнений всегда имеет нулевое решение 
Метод исследования и решения систем линейных уравнений, изложенный в доказательстве теорем 3 называется методом Гаусса.
Пример 1.Решить систему
Составим расширенную матрицу системы и приведем ее к ступенчатому виду:

Составим по полученной матрице ступенчатого вида систему линейных уравнений ступенчатого вида:
В полученной системе число уравнений равно числу неизвестных и полученная система имеет единственное решение, которое двигаясь вверх последовательно находим:
Решение системы 
Пример 2.Решить систему
Составим расширенную матрицу системы и приведем ее к ступенчатому виду:

Как решать систему уравнений
О чем эта статья:
8 класс, 9 класс, ЕГЭ/ОГЭ
Основные понятия
Алгебра в 8 и 9 классе становится сложнее. Но если изучать темы последовательно и регулярно практиковаться в тетрадке и онлайн — ходить на уроки математики будет не так страшно.
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в исходное уравнение получилось верное числовое равенство.
Например, возьмем 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.
Уравнением можно назвать, например, равенство 3 + x = 7 с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Система уравнений — это несколько уравнений, для которых надо найти значения неизвестных, каждое из которых соответствует данным уравнениям.
Так как существует множество уравнений, составленных с их использованием систем уравнений также много. Поэтому для удобства изучения существуют отдельные группы по схожим характеристикам. Рассмотрим способы решения систем уравнений.
Линейное уравнение с двумя переменными
Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.
Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому уравнению и обращает его в верное числовое равенство.
Теорема, которую нужно запомнить: если в линейном уравнение есть хотя бы один не нулевой коэффициент при переменной — его графиком будет прямая линия.
Вот алгоритм построения графика ax + by + c = 0, где a ≠ 0, b ≠ 0:
Дать переменной 𝑥 конкретное значение x = x₁, и найти значение y = y₁ при ax₁ + by + c = 0.
Дать x другое значение x = x₂, и найти соответствующее значение y = y₂ при ax₂ + by + c = 0.
Построить на координатной плоскости xy точки: (x₁; y₁); (x₂; y₂).
Провести прямую через эти две точки и вуаля — график готов.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Система двух линейных уравнений с двумя переменными
Для ax + by + c = 0 можно сколько угодно раз брать произвольные значение для x и находить значения для y. Решений в таком случае может быть бесчисленное множество.
Система линейных уравнений (ЛУ) с двумя переменными образуется в случае, когда x и y связаны не одним, а двумя уравнениями. Такая система может иметь одно решение или не иметь решений совсем. Выглядит это вот так:
Из первого линейного уравнения a₁x + b₁y + c₁ = 0 можно получить линейную функцию, при условии если b₁ ≠ 0: y = k₁x + m₁. График — прямая линия.
Из второго ЛУ a₂x + b₂y + c₂ = 0 можно получить линейную функцию, если b₂ ≠ 0: y = k₂x + m₂. Графиком снова будет прямая линия.
Можно записать систему иначе:
Множеством решений первого ЛУ является множество точек, лежащих на определенной прямой, аналогично и для второго ЛУ. Если эти прямые пересекаются — у системы есть единственное решение. Это возможно при условии, если k₁ ≠ k₂.
Две прямые могут быть параллельны, а значит, они никогда не пересекутся и система не будет иметь решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ ≠ m₂.
Две прямые могут совпасть, и тогда каждая точка будет решением, а у системы будет бесчисленное множество решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ = m₂.
Метод подстановки
Разберем решение систем уравнений методом подстановки. Вот алгоритм при переменных x и y:
Выразить одну переменную через другую из более простого уравнения системы.
Подставить то, что получилось на место этой переменной в другое уравнение системы.
Решить полученное уравнение, найти одну из переменных.
Подставить поочередно каждый из найденных корней в уравнение, которое получили на первом шаге, и найти второе неизвестное значение.
Записать ответ. Ответ принято записывать в виде пар значений (x; y).
Потренируемся решать системы линейных уравнений методом подстановки.
Пример 1
Решите систему уравнений:
x − y = 4
x + 2y = 10
Выразим x из первого уравнения:
x − y = 4
x = 4 + y
Подставим получившееся выражение во второе уравнение вместо x:
x + 2y = 10
4 + y + 2y = 10
Решим второе уравнение относительно переменной y:
4 + y + 2y = 10
4 + 3y = 10
3y = 10 − 4
3y = 6
y = 6 : 3
y = 2
Полученное значение подставим в первое уравнение вместо y и решим уравнение:
x − y = 4
x − 2 = 4
x = 4 + 2
x = 6
Ответ: (6; 2).
Пример 2
Решите систему линейных уравнений:
x + 5y = 7
3x = 4 + 2y
Сначала выразим переменную x из первого уравнения:
x + 5y = 7
x = 7 − 5y
Выражение 7 − 5y подставим вместо переменной x во второе уравнение:
3x = 4 + 2y
3 (7 − 5y) = 4 + 2y
Решим второе линейное уравнение в системе:
3 (7 − 5y) = 4 + 2y
21 − 15y = 4 + 2y
21 − 15y − 2y = 4
21 − 17y = 4
17y = 21 − 4
17y = 17
y = 17 : 17
y = 1
Подставим значение y в первое уравнение и найдем значение x:
x + 5y = 7
x + 5 = 7
x = 7 − 5
x = 2
Ответ: (2; 1).
Пример 3
Решите систему линейных уравнений:
x − 2y = 3
5x + y = 4
Из первого уравнения выразим x:
x − 2y = 3
x = 3 + 2y
Подставим 3 + 2y во второе уравнение системы и решим его:
5x + y = 4
5 (3 + 2y) + y = 4
15 + 10y + y = 4
15 + 11y = 4
11y = 4 − 15
11y = −11
y = −11 : 11
y = −1
Подставим получившееся значение в первое уравнение и решим его:
x − 2y = 3
x − 2 (−1) = 3
x + 2 = 3
x = 3 − 2
x = 1
Ответ: (1; −1).
Метод сложения
Теперь решим систему уравнений способом сложения. Алгоритм с переменными x и y:
При необходимости умножаем почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами.
Складываем почленно левые и правые части уравнений системы.
Решаем получившееся уравнение с одной переменной.
Находим соответствующие значения второй переменной.
Запишем ответ в в виде пар значений (x; y).
Система линейных уравнений с тремя переменными
Системы ЛУ с тремя переменными решают так же, как и с двумя. В них присутствуют три неизвестных с коэффициентами и свободный член. Выглядит так:
Решений в таком случае может быть бесчисленное множество. Придавая двум переменным различные значения, можно найти третье значение. Ответ принято записывать в виде тройки значений (x; y; z).
Если x, y, z связаны между собой тремя уравнениями, то образуется система трех ЛУ с тремя переменными. Для решения такой системы можно применять метод подстановки и метод сложения.
Решение задач
Разберем примеры решения систем уравнений.
Задание 1. Как привести уравнение к к стандартному виду ах + by + c = 0?
5x − 8y = 4x − 9y + 3
5x − 8y = 4x − 9y + 3
5x − 8y − 4x + 9y = 3
Задание 2. Как решать систему уравнений способом подстановки
Выразить у из первого уравнения:
Подставить полученное выражение во второе уравнение:
Найти соответствующие значения у:
Задание 3. Как решать систему уравнений методом сложения
- Решение систем линейных уравнений начинается с внимательного просмотра задачи. Заметим, что можно исключить у. Для этого умножим первое уравнение на минус два и сложим со вторым:
- Решаем полученное квадратное уравнение любым способом. Находим его корни:
- Найти у, подставив найденное значение в любое уравнение:
- Ответ: (1; 1), (1; -1).
Задание 4. Решить систему уравнений
Решим второе уравнение и найдем х = 2, х = 5. Подставим значение переменной х в первое уравнение и найдем соответствующее значение у.
Задание 5. Как решить систему уравнений с двумя неизвестными
При у = -2 первое уравнение не имеет решений, при у = 2 получается:
http://poisk-ru.ru/s39191t18.html
http://skysmart.ru/articles/mathematic/reshenie-sistem-uravnenij


























