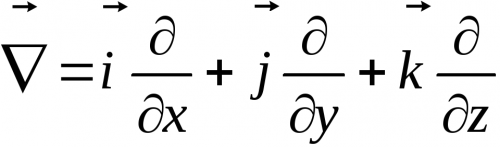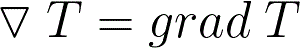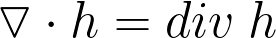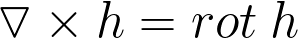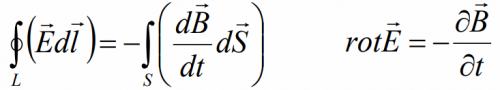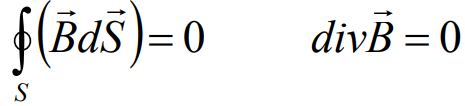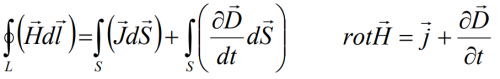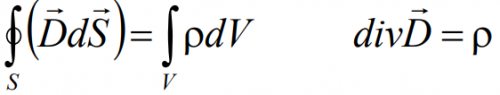Уравнения Максвелла для электромагнитного поля — основные законы электродинамики

Система уравнений Максвелла обязана своим названием и появлением Джеймсу Клерку Максвеллу, сформулировавшему и записавшему данные уравнения в конце 19 века.

Максвелл Джемс Кларк (1831 — 1879) был известным британским физиком и математиком, профессором Кембриджского университета в Англии.

Он практически объединил в своих уравнениях все накопленные к тому времени экспериментально полученные результаты касательно электричества и магнетизма и придал законам электромагнетизма четкую математическую форму. Основные законы электродинамики (уравнения Максвелла) были сформулированы в 1873 году.

Максвелл развил учение Фарадея об электромагнитном поле в стройную математическую теорию, из которой вытекала возможность волнового распространения электромагнитных процессов. При этом оказалось, что скорость распространения электромагнитных процессов равна скорости света (величина которой была уже известна из опытов).

Это совпадение послужило для Максвелла основанием к тому, чтобы высказать идею об общей природе электромагнитных и световых явлений, т.е. об электромагнитной природе света.

Созданная Джеймсом Максвеллом теория электромагнитных явлений нашла первое подтверждение в опытах Герца, впервые получившего электромагнитные волны.

В итоге эти уравнения сыграли главную роль в формировании точных представлений классической электродинамики. Уравнения Максвелла могут быть записаны в дифференциальной или интегральной форме. Практически они описывают сухим языком математики электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и в сплошных средах. К данным уравнениям можно добавить выражение для силы Лоренца, в этом случае мы получим полную систему уравнений классической электродинамики.

Чтобы понимать некоторые математические символы, использующиеся в дифференциальных формах уравнений Максвелла, для начала определим такую занятную вещь, как оператор набла.

Оператор набла (или оператор Гамильтона) — это векторный дифференциальный оператор, компоненты которого являются частными производными по координатам. Для нашего реального пространства, которое является трехмерным, адекватна прямоугольная система координат, для которой оператор набла определяется следующим образом:

где i, j и k – единичные координатные векторы

Оператор набла, будучи применен к полю тем или иным математическим образом, дает три возможные комбинации. Данные комбинации именуются:

Градиент — вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный скорости роста этой величины в этом направлении.

Дивергенция (расхождение) — дифференциальный оператор, отображающий векторное поле на скалярное (то есть, в результате применения к векторному полю операции дифференцирования получается скалярное поле), который определяет (для каждой точки), «насколько расходится входящее и исходящее из малой окрестности данной точки поле», точнее, насколько расходятся входящий и исходящий потоки.

Ротор (вихрь, ротация) — векторный дифференциальный оператор над векторным полем.

Теперь рассмотрим непосредственно уравнения Максвелла в интегральной (слева) и дифференциальной (справа) формах, содержащие в себе основные законы электрического и магнитного полей, включая электромагнитную индукцию.

Интегральная форма: циркуляция вектора напряженности электрического поля по произвольному замкнутому контуру прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром.

Дифференциальная форма: при всяком изменении магнитного поля возникает вихревое электрическое поле, пропорциональное скорости изменения индукции магнитного поля.

Физический смысл: всякое изменение магнитного поля во времени вызывает появление вихревого электрического поля.

Интегральная форма: поток индукции магнитного поля через произвольную замкнутую поверхность равен нулю. Это означает, что в природе нет магнитных зарядов.

Дифференциальная форма: поток силовых линий индукции магнитного поля из бесконечного элементарного объёма равен нулю, так как поле вихревое.

Физический смысл: источники магнитного поля в виде магнитных зарядов в природе отсутствуют.

Интегральная форма: циркуляция вектора напряженности магнитного поля по произвольному замкнутому контуру прямо пропорциональна суммарному току, пересекающему поверхность, охватываемую этим контуром.

Дифференциальная форма: вокруг любого проводника с током и вокруг любого переменного электрического поля существует вихревое магнитное поле.

Физический смысл: протекание тока проводимости по проводникам и изменения электрического поля во времени приводят к появлению вихревого магнитного поля.

Интегральная форма: поток вектора электростатической индукции через произвольную замкнутую поверхность, охватывающую заряды, прямо пропорционален суммарному заряду, расположенному внутри этой поверхности.

Дифференциальная форма: поток вектора индукции электростатического поля из бесконечного элементарного объема прямо пропорционален суммарному заряду, находящемуся в этом объёме.

Физический смысл: источником электрического поля является электрический заряд.

Система данных уравнений может быть дополнена системой так называемых материальных уравнений, которые характеризуют свойства заполняющей пространство материальной среды:

Уравнения Максвелла в интегральной форме

Система уравнений Максвелла является обобщением основных законов электрических и электромагнитных явлений. Она описывает абсолютно все электромагнитные явления. Основываясь на теории электромагнитного поля, эта система уравнений позволяет решать задачи, связанные с нахождением электрических и магнитных полей, создаваемых данным распределением электрических зарядов и токов. Уравнения Максвелла были отправной точкой для создания общей теории относительности Эйнштейна. Теория Максвелла раскрывает электромагнитную природу света. Уравнения были сформулированы Дж. Максвелом в шестидесятых годах XIX века на основе обобщения эмпирических законов и развития идей ученых, изучавших перед ним электромагнитные явления (законы Кулона, Био-Савара, Ампера и в частности, исследование Фарадея). Сам Максвелл записал 20 уравнений с 20 неизвестными в дифференциальной форме, которые впоследствии были преобразованы. Современная форма Максвелла дана немецким физиком Г. Герцем и английским физиком О. Хевисайдом. Запишем уравнения с использованием системы Гаусса единиц.

Система уравнений Максвелла

В состав системы уравнений Максвелла входят четыре уравнения.

Это закон Фарадея (закон электромагнитной индукции).

где — напряженность электрического поля, — вектор магнитной индукции, c — скорость света в вакууме.

Это уравнение говорит, что ротор напряженности электрического поля равен скорости потока (т. Е. Скорости изменения во времени) вектора магнитной индукции через эту схему.

Уравнение (1.1) является первым уравнением Максвелла в дифференциальной форме.

Одно и то же уравнение можно записать в интегральной форме, тогда оно примет следующий вид:

где Bn — проекция на нормаль к площади dS вектора магнитной индукции,

Циркуляция вектора напряженности электрического поля вдоль замкнутой петли L (индукционная э.д.с.) определяется скоростью изменения потока вектора магнитной индукции через поверхность, ограниченную данной схемой. Знак минус согласно правилу Lenc означает направление тока индукции.

Согласно Максвеллу, закон электромагнитной индукции (и это именно он) справедлив для любой замкнутой петли, произвольно выбранной в переменном магнитном поле.

Смысл этого уравнения: переменное магнитное поле в любой точке пространства создает вихревое электрическое поле.

Второе уравнение Максвелла:

где — вектор магнитной интенсивности, плотность электрического тока, — вектор электрического смещения.

Это уравнение Максвелла является обобщением эмпирического закона Би-Савара, что магнитные поля возбуждаются электрическими токами. Смысл второго уравнения состоит в том, что источником вихревого магнитного поля является также переменное электрическое поле, магнитное действие которого характеризуется током смещения. ( плотность тока смещения).

В интегральной форме второе уравнение Максвелла (теорема о циркуляции магнитного поля) представляется следующим образом:

Циркуляция вектора магнитного поля вдоль произвольного контура равна алгебраической сумме токов проводимости и тока смещения, связанного с контуром.

Когда Максвелл вводил уравнения (более ста лет тому назад!), природа электромагнитного поля была не понятна. В настоящее время природа поля выяснена, и стало ясно, что может быть названo «током» лишь формально. По pяду расчетных соображений такое название, не придавая ему прямого физического смысла, целесообразно сохранить, что в электротехнике и делается. По этой же причине вектор D, входящий в выражение для тока смещения, называют вектором электрического смещения.

Помимо первых двух уравнений в систему уравнений Максвелла входит теорема Гаусса-Остроградского для электрического и магнитного полей:

где —плотность электрического заряда.

Что в интегральном виде представляет собой следующее:

где поток электрического смещения — поток магнитной индукции сквозь замкнутую поверхность, охватывающую свободный заряд q.

Смысл уравнения 3.2. Электрический заряд – источник электрической индукции.

Уравнение 4.2 выражает факт отсутствия свободных магнитных зарядов.

Полная система уравнений Максвелла в дифференциальном виде (характеризует поле в каждой точке пространства):

Полная система уравнений Максвелла в интегральном виде

Полная система уравнений Максвелла в интегральном виде (интегральная форма записи уравнений облегчает их физическую интерпретацию так ка делает их визуально ближе к известным эмпирическим законам):

Систему уравнений Максвелла дополняют «материальными уравнениями», связывающими векторы c величинами, описывающими электрические и магнитные свойства среды.

где – относительная диэлектрическая проницаемость, – относительная магнитная проницаемость, -удельная электропроводность, – электрическая постоянная, — магнитная постоянная. Среда предполагается изотропной, неферрромагнитной, несегнетоэлектрической.

На границе раздела двух сред выполняются граничные условия:

где — поверхностная плотность свободных зарядов, n- единичный вектор нормали к границе раздела, проведенный из среды 2 в 1, — единичный вектор, касательный к границе, — проекция вектора плотности поверхностных токов проводимости на единичный вектор.

Данные уравнения выражают непрерывность нормальных составляющих вектора магнитной индукции и скачок нормальных составляющих вектора смещения. Непрерывность касательных составляющих вектора напряженностей электрического поля на границе раздела и скачок этих составляющих для напряженности магнитного поля.

Примеры решения задач

Из системы уравнений Максвелла получить уравнения непрерывности токов и закон сохранения заряда.

Проведем для него операцию дивергенции ( или ). Получим:

из системы уравнений Максвелла знаем, что

Подставим (с) в (b) получим:

или в интегральной форме:

Соответственно для замкнутых изолированных областей получим:

Это уравнение непрерывности для тока, содержащее в себе закон сохранения заряда – один из фундаментальных принципов, который подтверждается экспериментом.

Доказать, что сумма токов проводимости и тока смещения, сцепленных с контуром, действительно непрерывна и, следовательно, полный ток, сцепленный с любым контуром, не зависит от выбора поверхности, натянутой на этот контур.

Допустим, что в произвольном магнитном поле на некоторый контур натянуты две произвольные поверхности S1 и S2. (рис. 3)

Знак вектора потока , сцепленного с контуром, связывается правилом правого винта с направлением обхода контура L. В частности, пpи том направлении силовых линий, которое изображено на поток D сцепленный, с контуром для поверхностей, S1 и S2 нужно считать положительным. Рассмотрим замкнутую полость, ограниченную поверхностью S1 + S2. В соответствии с теоремой Гаусса для нее можно записать уравнение:

Здесь q — сумма зарядов, попадающих в рассматриваемую полость, ограниченную поверхностью S1 + S2.Продифференцируем обе части этого уравнения по времени:

Преобразуем раздельно левую и правую части этого уравнения. Поток вектора D сквозь замкнутую поверхность можно представить следующим образом:

Линии векторного поля D входят в замкнутую полость через поверхность S2. По определению они создают отрицательный поток. Если рассматривать поток, сцепленный с контуром, то, используя правило знаков, его необходимо считать положительным. Следовательно, выражение (c) применительно к контуру, можно записать так:

Уясним, что собой представляет правая часть уравнения (b). Производная от полного заряда, заключенного в полости, стоящая в правой части (b), показывает, на какую величину изменяется заряд в полости в секунду. За счет чего может изменяться заряд в полости? В силу закона сохранения заряда он может изменяться только за счет неравных токов входящих и выходящих из нее. Пpи равенстве этих токов полный заряд в полости оставался бы постоянным. Причём, токи, входящие в полость, следует считать положительными (они увеличивают заряд в полости), а токи, выходящие из нее, — отрицательными. Таким образом, уравнение (b) можно представить следующим образом:

МА́КСВЕЛЛА УРАВНЕ́НИЯ

МА́КСВЕЛЛА УРАВНЕ́НИЯ, ос­но­во­по­ла­гаю­щие урав­не­ния клас­сич. мак­ро­ско­пич. элек­тро­ди­на­ми­ки, опи­сы­ваю­щие за­ко­но­мер­но­сти элек­тро­маг­нит­ных яв­ле­ний в сплош­ной сре­де или ва­куу­ме (в пре­неб­ре­же­нии кван­то­вы­ми яв­ле­ния­ми). Тео­рия элек­тро­маг­нит­но­го поля бы­ла раз­ра­бо­та­на Дж. К. Мак­свел­лом в 1856–73. В М. у. обоб­ще­ны ра­нее ус­та­нов­лен­ные опыт­ные за­ко­ны элек­трич. и маг­нит­ных яв­ле­ний, и эти за­ко­ны объ­е­ди­не­ны с кон­цеп­ци­ей М. Фа­ра­дея об элек­тро­маг­нит­ном по­ле, обес­пе­чи­ваю­щем взаи­мо­дей­ст­вие ме­ж­ду уда­лён­ны­ми за­ря­жен­ны­ми те­ла­ми (т. н. тео­рия близ­ко­дей­ст­вия). В ори­ги­наль­ном из­ло­же­нии Мак­свел­ла бы­ло соз­на­тель­но при­ве­де­но из­бы­точ­ное чис­ло урав­не­ний; при этом Мак­свелл ис­поль­зо­вал ма­те­ма­тич. ап­па­рат ква­тер­нио­нов Га­миль­то­на. Совр. фор­му М. у. с ис­поль­зо­ва­ни­ем век­тор­но­го ис­чис­ле­ния при­да­ли Г. Р. Герц и О. Хе­ви­сайд . М. у. свя­зы­ва­ют век­тор­ные по­ле­вые ве­ли­чи­ны (яв­ляю­щие­ся функ­ция­ми ко­ор­ди­нат и вре­ме­ни) с ис­точ­ни­ка­ми элек­тро­маг­нит­но­го по­ля – рас­пре­де­лён­ны­ми в про­стран­ст­ве и из­ме­няю­щи­ми­ся во вре­ме­ни элек­трич. за­ря­да­ми и то­ка­ми. М. у. име­ют вид (диф­фе­рен­ци­аль­ная фор­ма М. у. в СИ): $$\textrm\,\boldsymbol E=-\frac<\partial \boldsymbol B><\partial t>,\quad \textrm\,\boldsymbol H=\boldsymbol j+\frac<\partial \boldsymbol D><\partial t>,\\ \textrm