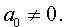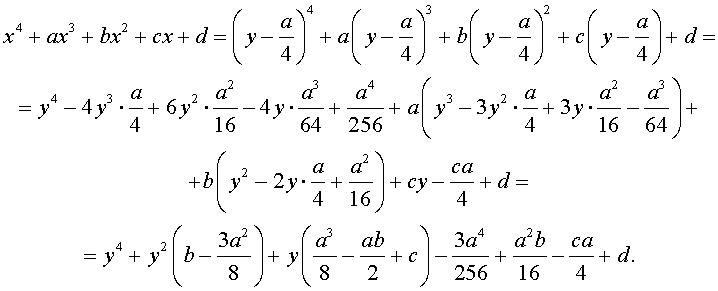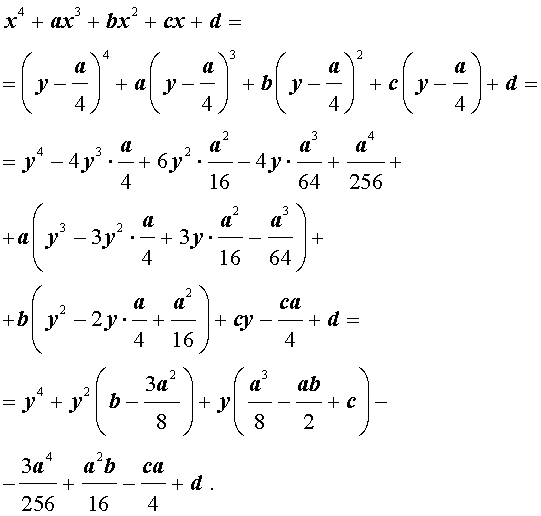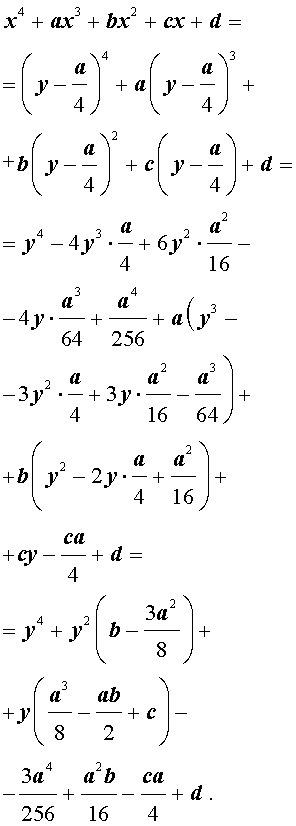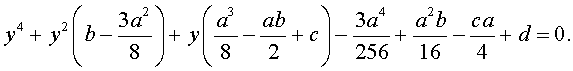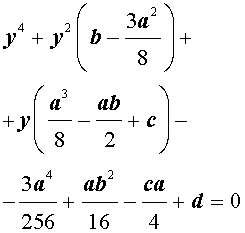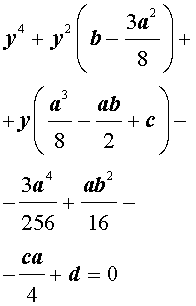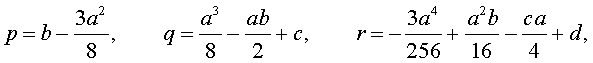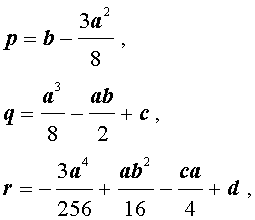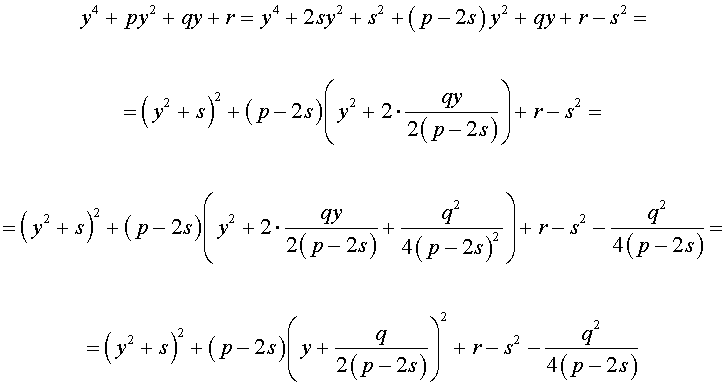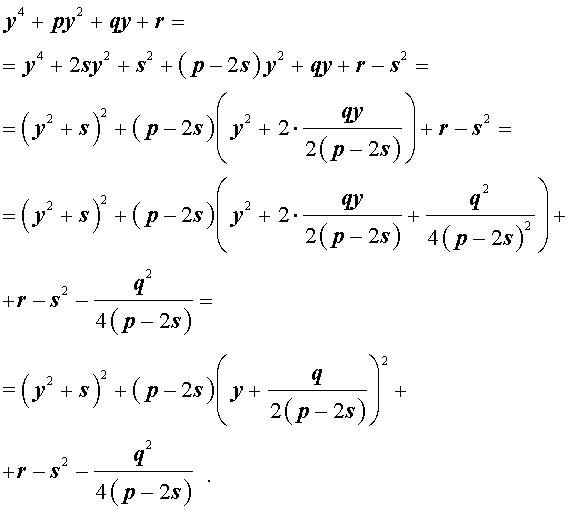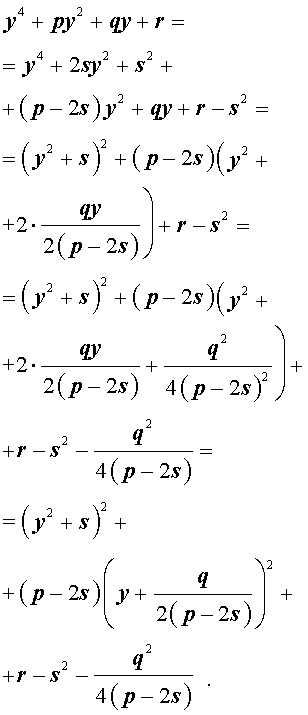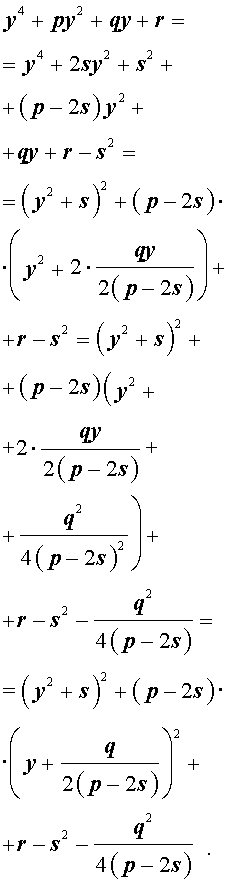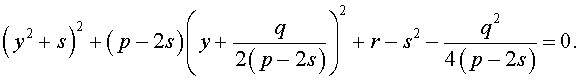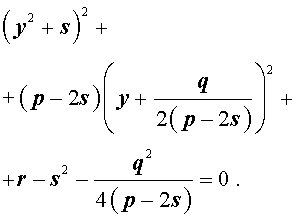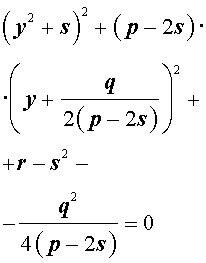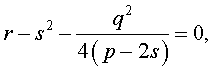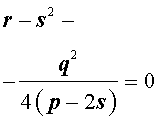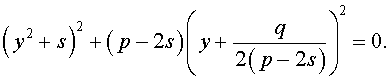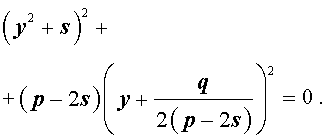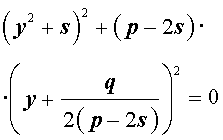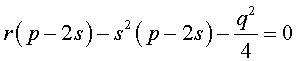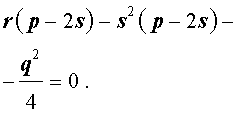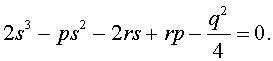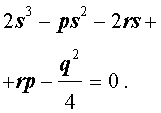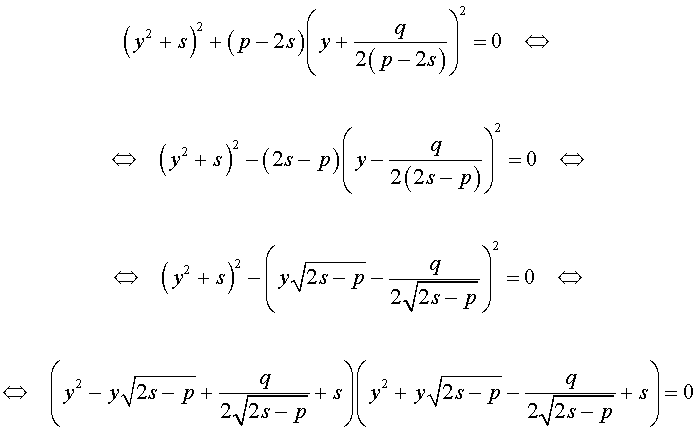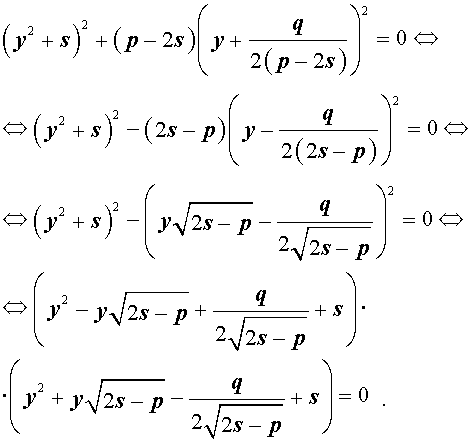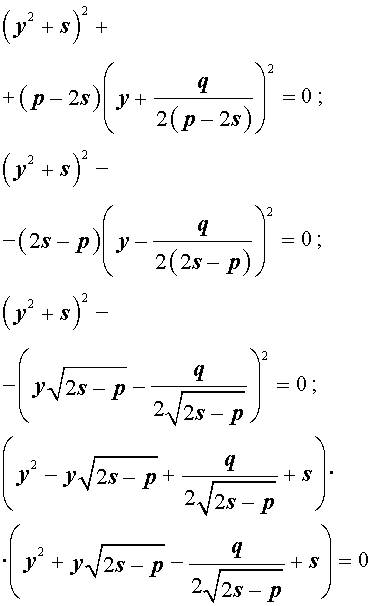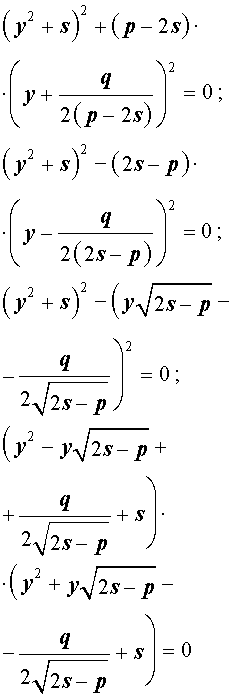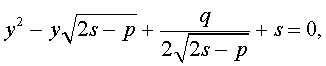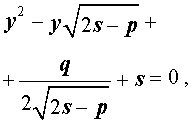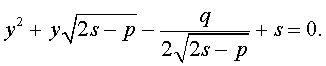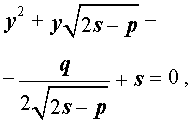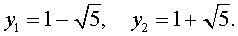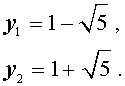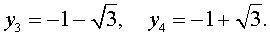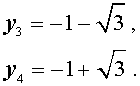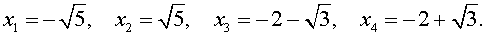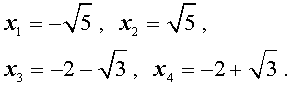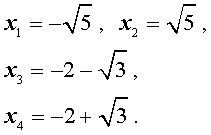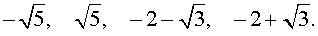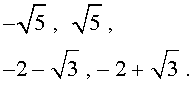Решение уравнений 4-ой степени. Метод Феррари
 Схема метода Феррари Схема метода Феррари |
 Приведение уравнений 4-ой степени Приведение уравнений 4-ой степени |
 Разложение на множители. Кубическая резольвента Разложение на множители. Кубическая резольвента |
 Пример решения уравнения 4-ой степени Пример решения уравнения 4-ой степени |
Схема метода Феррари
Целью данного раздела является изложение метода Феррари , с помощью которого можно решать уравнения четвёртой степени
| a0x 4 + a1x 3 + a2x 2 + + a3x + a4 = 0, | (1) |
где a0, a1, a2, a3, a4 – произвольные вещественные числа, причем
Метод Феррари состоит из двух этапов.
На первом этапе уравнения вида (1) приводятся к уравнениям четвертой степени, у которых отсутствует член с третьей степенью неизвестного.
На втором этапе полученные уравнения решаются при помощи разложения на множители, однако для того, чтобы найти требуемое разложение на множители, приходится решать кубические уравнения.
Приведение уравнений 4-ой степени
Разделим уравнение (1) на старший коэффициент a0 . Тогда оно примет вид
| x 4 + ax 3 + bx 2 + + cx + d = 0, | (2) |
где a, b, c, d – произвольные вещественные числа.
Сделаем в уравнении (2) замену
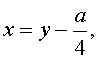 | (3) |
где y – новая переменная.
то уравнение (2) принимает вид
В результате уравнение (2) принимает вид
Если ввести обозначения
то уравнение (4) примет вид
| y 4 + py 2 + qy + r = 0, | (5) |
где p, q, r – вещественные числа.
Первый этап метода Феррари завершён.
Разложение на множители. Кубическая резольвента
Добавив и вычитая в левой части уравнения (5) выражение
где s – некоторое число, которое мы определим чуть позже, из (5) получим
Следовательно, уравнение (5) принимает вид
Если теперь выбрать число s так, чтобы оно являлось каким-нибудь решением уравнения
то уравнение (6) примет вид
Избавляясь от знаменателя, уравнение (7) можно переписать в виде
или, раскрыв скобки, — в виде
Полученное кубическое уравнение (9), эквивалентное уравнению (7), называют кубической резольвентой уравнения 4-ой степени (5).
Если какое-нибудь решение кубической резольвенты (9) найдено, то уравнение (8) можно решить, разложив его левую часть на множители с помощью формулы сокращенного умножения «Разность квадратов».
Таким образом, для решения уравнения (8) остаётся решить квадратное уравнение
а также квадратное уравнение
Вывод метода Феррари завершен.
Пример решения уравнения 4-ой степени
Пример . Решить уравнение
| x 4 + 4x 3 – 4x 2 – – 20x – 5 = 0. | (12) |
Решение . В соответствии с (3) сделаем в уравнении (12) замену
| x = y – 1. | (13) |
то в результате замены (13) уравнение (12) принимает вид
| y 4 – 10y 2 – 4y + 8 = 0. | (14) |
В соответствии с (5) для коэффициентов уравнения (14) справедливы равенства
| p = – 10, q = – 4, r = 8. | (15) |
В силу (9) и (15) кубической резольвентой для уравнения (14) служит уравнение
которое при сокращении на 2 принимает вид:
| s 3 + 5s 2 – 8s – 42 = 0. | (16) |
| s = – 3. | (17) |
Подставляя значения (15) и (17) в формулу (10), получаем уравнение
Подставляя значения (15) и (17) в формулу (11), получаем уравнение
В завершение, воспользовавшись формулой (13), из (18) и (19) находим корни уравнения (12):
Замечание . При решении примера мы попутно получили разложение левой части уравнения (14) на множители:
| y 4 – 10y 2 – 4y + 8 = = (y 2 – 2y – 4) (y 2 + + 2y – 2). | (20) |
Предоставляем посетителю нашего сайта возможность убедиться в справедливости равенства (19) в качестве несложного упражнения.
Решение уравнений четвертой степени
Для уравнений четвертой степени применимы все те общие схемы решения уравнений высших степеней, что мы разбирали в предыдущем материале. Однако существует ряд нюансов в решении двучленных, биквадратных и возвратных уравнений, на которых мы хотели бы остановиться подробнее.
Также в статье мы разберем искусственный метод разложения многочлена на множители, решение в радикалах и метод Феррари, который используется для того, чтобы свести решение уравнения четвертой степени к кубическому уравнению.
Решение двучленного уравнения четвертой степени
Это простейший тип уравнений четвертой степени. Запись уравнения имеет вид A x 4 + B = 0 .
Для решения этого типа уравнений применяются формулы сокращенного умножения:
A x 4 + B = 0 x 4 + B A = 0 x 4 + 2 B A x 2 + B A — 2 B A x 2 = 0 x 2 + B A 2 — 2 B A x 2 = 0 x 2 — 2 B A 4 x + B A x 2 + 2 B A 4 x + B A = 0
Остается лишь найти корни квадратных трехчленов.
Решить уравнение четвертой степени 4 x 4 + 1 = 0 .
Решение
Для начала проведем разложение многочлена 4 x 4 + 1 на множители:
4 x 4 + 1 = 4 x 4 + 4 x 2 + 1 = ( 2 x 2 + 1 ) 2 — 4 x 2 = 2 x 2 — 2 x + 1 ( 2 x 2 + 2 x + 1 )
Теперь найдем корни квадратных трехчленов.
2 x 2 — 2 x + 1 = 0 D = ( — 2 ) 2 — 4 · 2 · 1 = — 4 x 1 = 2 + D 2 · 2 = 1 2 + i x 2 = 2 — D 2 · 2 = 1 2 — i
2 x 2 + 2 x + 1 = 0 D = 2 2 — 4 · 2 · 1 = — 4 x 3 = — 2 + D 2 · 2 = — 1 2 + i x 4 = — 2 — D 2 · 2 = — 1 2 — i
Мы получили четыре комплексных корня.
Ответ: x = 1 2 ± i и x = — 1 2 ± i .
Решение возвратного уравнения четвертой степени
Возвратные уравнения четвертого порядка имеют вид A x 4 + B x 3 + C x 2 + B x + A = 0
х = 0 не является корнем этого уравнения: A · 0 4 + B · 0 3 + C · 0 2 + B · 0 + A = A ≠ 0 . Поэтому на x 2 можно смело разделить обе части этого уравнения:
A x 4 + B x 3 + C x 2 + B x + A = 0 A x 2 + B x + C + B x + A x 2 = 0 A x 2 + A x 2 + B x + B x + C = 0 A x 2 + 1 x 2 + B x + 1 x + C = 0
Проведем замену переменных x + 1 x = y ⇒ x + 1 x 2 = y 2 ⇒ x 2 + 1 x 2 = y 2 — 2 :
A x 2 + 1 x 2 + B x + 1 x + C = 0 A ( y 2 — 2 ) + B y + C = 0 A y 2 + B y + C — 2 A = 0
Так мы проведи сведение возвратного уравнения четвертой степени к квадратному уравнению.
Найти все комплексные корни уравнения 2 x 4 + 2 3 + 2 x 3 + 4 + 6 x 2 + 2 3 + 2 x + 2 = 0 .
Решение
Симметрия коэффициентов подсказывает нам, что мы имеем дело с возвратным уравнением четвертой степени. Проведем деление обеих частей на x 2 :
2 x 2 + 2 3 + 2 x + 4 + 6 + 2 3 + 2 x + 2 x 2 = 0
2 x 2 + 2 x 2 + 2 3 + 2 x + 2 3 + 2 x + 4 + 6 + = 0 2 x 2 + 1 x 2 + 2 3 + 2 x + 1 x + 4 + 6 = 0
Проведем замену переменной x + 1 x = y ⇒ x + 1 x 2 = y 2 ⇒ x 2 + 1 x 2 = y 2 — 2
2 x 2 + 1 x 2 + 2 3 + 2 x + 1 x + 4 + 6 = 0 2 y 2 — 2 + 2 3 + 2 y + 4 + 6 = 0 2 y 2 + 2 3 + 2 y + 6 = 0
Решим полученное квадратное уравнение:
D = 2 3 + 2 2 — 4 · 2 · 6 = 12 + 4 6 + 2 — 8 6 = = 12 — 4 6 + 2 = 2 3 — 2 2 y 1 = — 2 3 — 2 + D 2 · 2 = — 2 3 — 2 + 2 3 — 2 4 = — 2 2 y 2 = — 2 3 — 2 — D 2 · 2 = — 2 3 — 2 — 2 3 + 2 4 = — 3
Вернемся к замене: x + 1 x = — 2 2 , x + 1 x = — 3 .
Решим первое уравнение:
x + 1 x = — 2 2 ⇒ 2 x 2 + 2 x + 2 = 0 D = 2 2 — 4 · 2 · 2 = — 14 x 1 = — 2 — D 2 · 2 = — 2 4 + i · 14 4 x 2 = — 2 — D 2 · 2 = — 2 4 — i · 14 4
Решим второе уравнение:
x + 1 x = — 3 ⇒ x 2 + 3 x + 1 = 0 D = 3 2 — 4 · 1 · 1 = — 1 x 3 = — 3 + D 2 = — 3 2 + i · 1 2 x 4 = — 3 — D 2 = — 3 2 — i · 1 2
Ответ: x = — 2 4 ± i · 14 4 и x = — 3 2 ± i · 1 2 .
Решение биквадратного уравнения
Биквадратные уравнения четвертой степени имеют вид A x 4 + B x 2 + C = 0 . Мы можем свести такое уравнение к квадратному A y 2 + B y + C = 0 путем замены y = x 2 . Это стандартный прием.
Решить биквадратное уравнение 2 x 4 + 5 x 2 — 3 = 0 .
Решение
Выполним замену переменной y = x 2 , что позволит нам свести исходное уравнение к квадратному:
2 y 2 + 5 y — 3 = 0 D = 5 2 — 4 · 2 · ( — 3 ) = 49 y 1 = — 5 + D 2 · 2 = — 5 + 7 4 = 1 2 y 2 = — 5 — D 2 · 2 = — 5 — 7 4 = — 3
Следовательно, x 2 = 1 2 или x 2 = — 3 .
Первое равенство позволяет нам получить корень x = ± 1 2 . Второе равенство не имеет действительных корней, зато имеет комплексно сопряженных корней x = ± i · 3 .
Ответ: x = ± 1 2 и x = ± i · 3 .
Найти все комплексные корни биквадратного уравнения 16 x 4 + 145 x 2 + 9 = 0 .
Решение
Используем метод замены y = x 2 для того, чтобы свести исходное биквадратное уравнение к квадратному:
16 y 2 + 145 y + 9 = 0 D = 145 2 — 4 · 16 · 9 = 20449 y 1 = — 145 + D 2 · 16 = — 145 + 143 32 = — 1 16 y 2 = — 145 — D 2 · 16 = — 145 — 143 32 = — 9
Поэтому, в силу замены переменной, x 2 = — 1 16 или x 2 = — 9 .
Ответ: x 1 , 2 = ± 1 4 · i , x 3 , 4 = ± 3 · i .
Решение уравнений четвертой степени с рациональными корнями
Алгоритм нахождения рациональных корней уравнения четвертой степени приведен в материале «Решение уравнений высших степеней».
Решение уравнений четвертой степени по методу Феррари
Уравнения четвертой степени вида x 4 + A x 3 + B x 2 + C x + D = 0 в общем случае можно решить с применением метода Феррари. Для этого необходимо найти y 0 . Это любой из корней кубического уравнения y 3 — B y 2 + A C — 4 D y — A 2 D + 4 B D — C 2 = 0 . После этого необходимо решить два квадратных уравнения x 2 + A 2 x + y 0 2 + A 2 4 — B + y 0 x 2 + A 2 y 0 — C x + y 0 2 4 — D = 0 , у которых подкоренное выражение является полным квадратом.
Корни, полученные в ходе вычислений, будут корнями исходного уравнения четвертой степени.
Найти корни уравнения x 4 + 3 x 3 + 3 x 2 — x — 6 = 0 .
Решение
Имеем А = 3 , В = 3 , С = — 1 , D = — 6 . Применим метод Феррари для решения данного уравнения.
Составим и решим кубическое уравнение:
y 3 — B y 2 + A C — 4 D y — A 2 D + 4 B D — C 2 = 0 y 3 — 3 y 2 + 21 y — 19 = 0
Одним из корней кубического уравнения будет y 0 = 1 , так как 1 3 — 3 · 1 2 + 21 · 1 — 19 = 0 .
Запишем два квадратных уравнения:
x 2 + A 2 x + y 0 2 ± A 2 4 — B + y 0 x 2 + A 2 y 0 — C x + y 0 2 4 — D = 0 x 2 + 3 2 x + 1 2 ± 1 4 x 2 + 5 2 x + 25 4 = 0 x 2 + 3 2 x + 1 2 ± 1 2 x + 5 2 2 = 0
x 2 + 3 2 x + 1 2 + 1 2 x + 5 2 = 0 или x 2 + 3 2 x + 1 2 — 1 2 x — 5 2 = 0
x 2 + 2 x + 3 = 0 или x 2 + x — 2 = 0
Корнями первого уравнения будут x = — 1 ± i · 2 , корнями второго х = 1 и х = — 2 .
Ответ: x 1 , 2 = — 1 ± i 2 , x 3 = 1 , x 4 = — 2 .
Презентация педагогического проекта по теме: “Методы решения уравнений четвертой степени”
Презентация педагогического проекта
Просмотр содержимого документа
«Презентация педагогического проекта по теме: “Методы решения уравнений четвертой степени”»
Методы решения уравнений четвёртой степени
Выполнила Чурина Елена Вениаминовна, учитель математики первой квалификационной категории
МБОУСОШ №1 г. Южи
Актуальность — Как все знают, в математике одна из важнейших вещей- это уравнения. Чаще всего решаются линейные либо квадратные уравнения, но не мало важны уравнения 4 степени, которые решить сможет не каждый. Чтобы решать такие уравнения было проще, нужно выбрать тот способ, который тебе более понятен.
Задания с уравнениями высших степеней есть в контрольных измерительных материалах при проведении государственной итоговой аттестации. Значит, ученики должны уметь решать уравнения не только 2 степени, но и выше. А это умеет делать далеко не каждый.
Цель работы: узнать и разобрать методы решения уравнений 4-й степени.
Достижение поставленной цели требует решения следующих основных задач:
1) Изучить литературу по истории приемов решения уравнений 4-й стпени
2)Обобщить накопленные знания об уравнениях4-й степени и способах их решения.
3) Сделать выводы.
4)Разработать дидактический материал для проведения практикума по решению уравнений 4-й степени с использованием новых приемов в помощь ученикам, увлеченным математикой и учителям, ведущим факультативные занятия.
Я выдвинула следующую гипотезу:
существует универсальный способ для решения всех видов уравнений 4-степеней.
В первой главе я рассмотрела теоретическую составляющую данного вопроса, а именно определение и теорему Виета для уравнения четвертой степени.
Уравнение четвёртой степени —алгебраическое уравнение вида:
при этом a ≠0 и где a , b , c , d , e — любые числа.
Теорема Виета для уравнения четвёртой степени
решения уравнения четвертой степени
На первом этапе уравнения 4-й степни приводятся к уравнениям четвертой степени, у которых отсутствует член с третьей степенью неизвестного.
На втором этапе полученные уравнения решаются при помощи разложения на множители, однако для того, чтобы найти требуемое разложение на множители, приходится решать кубические уравнения.
Решение уравнений по схеме Горнера
Схема Горнера (или правило Горнера, метод Горнера) — алгоритм вычисления значения многочлена, записанного в виде суммы одночленов, при заданном значении переменной. Метод Горнера позволяет найти корни многочлена.
Схема Горнера является простым
алгоритмом для деления многочлена .
Разложение на множители Кубическая резольвента
Резольвента алгебраического уравнения — это алгебраическое уравнение с коэффициентами, рационально зависящими от коэффициентов данного уравнения и такое, что знание корней этого уравнения позволяет решить исходное уравнение путём решения более простых уравнений (то есть таких, что их степень не больше степени данного уравнения).
Выделение полного квадрата
Этот метод основан на использовании формул:
а 2 -b 2 =( а -b)(а+b) a 2 +2ab+b 2 =(a+b) 2 a 2 −2ab+b 2 =(a−b) 2
а 3 + b 3 =(а+ b )(а 2 -а b + b 2 ) а 3 — b 3 =(а- b )(а 2 +а b + b 2 ) (а+ b ) 3 =а 3 +3а 2 b +3а b 2 + b 3
(а- b ) 3 = а 3 -3а 2 b +3а b 2 — b 3 ,
Биквадратные уравнения. Способ замены

Способом группировки можно решить уравнение 4 степени.
Чтобы разложить уравнение на множители, надо сгруппировать слагаемые по парам. Мы должны сгруппировать слагаемые по парам таким образом, чтобы при вынесении общего множителя за скобки у слагаемых был одинаковый множитель.
Решим на примере.
2х 4 -5х 3 -2х 2 +5х=0
(2х 4 -5х 3 )+( -2х 2 +5х)=0
х=0 или 2х-5=0 или х-1=0 или х+1=0
х 1 =0 х 2 =2,5 х 3 =1 х 4 =-1
По свободному члену (теорема Безу)
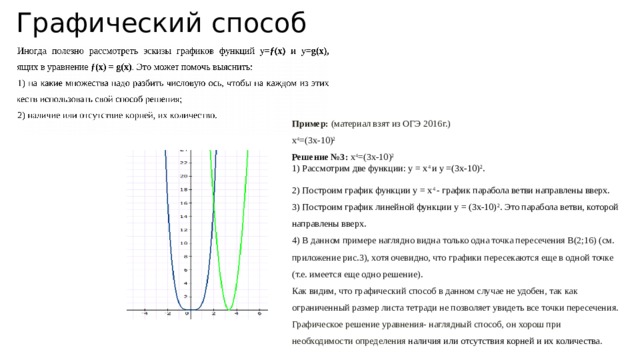
Пример: (материал взят из ОГЭ 2016г.)
Решение №3: x 4 =(3x-10) 2
1) Рассмотрим две функции: у = х 4 и у =(3х-10) 2 .
2) Построим график функции у = х 4 — график парабола ветви направлены вверх.
3) Построим график линейной функции у = (3х-10) 2 . Это парабола ветви, которой направлены вверх.
4) В данном примере наглядно видна только одна точка пересечения В(2;16) (см. приложение рис.3), хотя очевидно, что графики пересекаются еще в одной точке (т.е. имеется еще одно решение).
Как видим, что графический способ в данном случае не удобен, так как ограниченный размер листа тетради не позволяет увидеть все точки пересечения.
Графическое решение уравнения- наглядный способ, он хорош при необходимости определения наличия или отсутствия корней и их количества .
Тренировочные задания для отработки различных способов решения уравнений 4-й степени.
№ 1 Решите уравнения способом замены: , б) X 4 -2 x 2 -8=0,
в) x 4 -8 x 2 -9=0, г) x 4 -7 x 2 +12=0, д) 3 x 4 -13 x 2 +4=0, е) 2 x 4 -19 x 2 +9=0,
ж) 3 x 4 -13 x 2 +4=0, з) ( x 2 +4 x )( x 2 +4 x -17)=60=0, и) ( x 2 -5 x )( x 2 -5 x +10)+24=0,
к)( x 2 -3 x ) 2 -2( x 2 -3 x )=8, л) ( x 2 + x ) 2 -11( x 2 + x )=12.
№ 2 Решите уравнения, раскладывая левую часть на множители способом группировки:
а) 2 x 4 -5 x 3 +2 x 2 -5 x =0,
б) 6 x 4 -3 x 3 +12 x 2 -6 x =0,
в) 2 x 4 +3 x 3 -8 x 2 -12 x =0,
г) 2 x 4 -5 x 3 -18 x 2 +45 x =0.
№ 3 Решите уравнения по свободному члену
а) 2 x 4 – 3 x 3 – 7 x 2 –15 x + 50 =0 б)х 4 -4х 2 +3х+2=0
в) х 4 +2х 3 -7х 2 -8х+12=0
- 1. Уравнения высших степеней решали еще более 500 тыс. лет назад.
- 2. Есть много способов решения уравнений 4-й степеней. Некоторые из них довольно сложные, а некоторые помогут быстро решить задания на ОГЭ.
- 3. Уравнения 4-й степеней играют немалую роль в развитии математики. Лишь немногие из учащихся умеют решать такие уравнения. Эти методы решения уравнений высших степеней непросты в применении, но они всё равно могут заинтересовать увлекающихся математикой учеников.
В ходе работы я разобрала 8 способов решения уравнений 4 степени. Но это далеко не все способы решения таких уравнений. Я доказала свою гипотезу. Существует универсальный метод решения уравнений четвертой степени. Эту формулу связывают с именем Людовико Феррари.
Лишь немногие из учащихся умеют решать такие уравнения. Методы решения уравнений высших степеней непросты в применении, но они могут заинтересовать увлекающихся математикой учеников.
Алгебра. 9 класс:учебник для общеобразовательных организаций / А45 Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под редакцией С. А. Теляковского. – 4-е издание – М.: Просвещение, 2017. – 287 с.: ил. – ISBN 978-5-09-046396-6.
- . М.Л. Галицкий, А.М. Гольдман, Л.М. Звавич «Сборник задач по алгебре для 8-9 классов». Учебное пособие для учащихся школ и классов с углубленным изучением математики -Москва «Просвещение», 1999.
- В.В. Бардушкин, И.Б. Кожухов, А.А. Прокофьев, А.М. Ревякин, А.М. Терещенко «Письменный вступительный экзамен по математике» — Москва «Лист», 1998.
- Н.В. Бурмистрова, Н.Г. Старостенкова «Функции и их графики». Учебное пособие — Саратов «Лицей», 2003.
- М.А.Еремин «Уравнения высших степеней» — Арзамас, 2003.
- А.Г.Курош «Алгебраические уравнения произвольных степеней» — М.:Наука, 1975.
- Л.М.Лоповок «1000 проблемных задач по математике» — М.: Просвящение, 1995.
- И.Р.Шафаревич «Популярные лекции по математике. О решении уравнений высших степеней» Вып.15 – М.: Наука, 1954.
- 10. https://zaochnik.com/spravochnik/matematika/systems/reshenie-uravnenij-vysshih-stepenej/
- 11. http://www.cleverstudents.ru/equations/equations_of_higher_degree.html
- 12. https://ru.wikipedia.org/wiki/Уравнение_четвёртой_степени
http://zaochnik.com/spravochnik/matematika/systems/reshenie-uravnenij-chetvertoj-stepeni/
http://multiurok.ru/files/prezentatsiia-pedagogicheskogo-proekta-po-teme-met.html