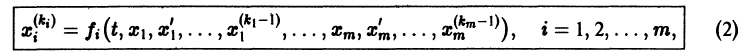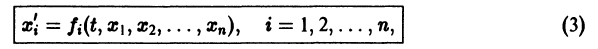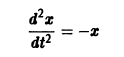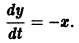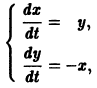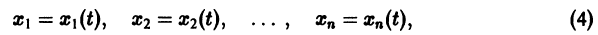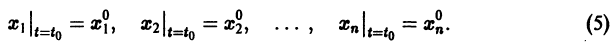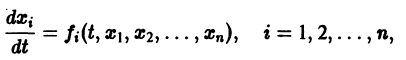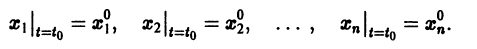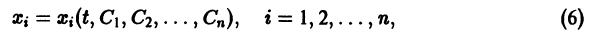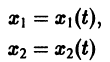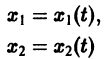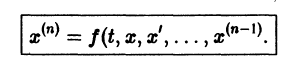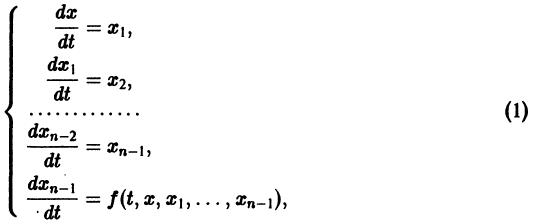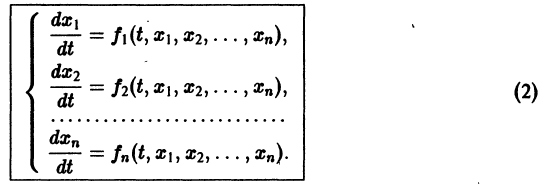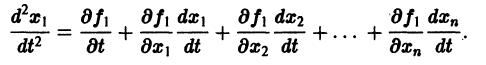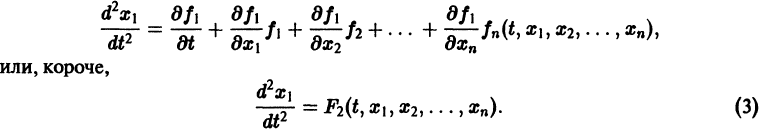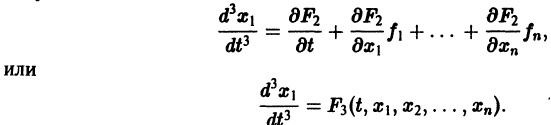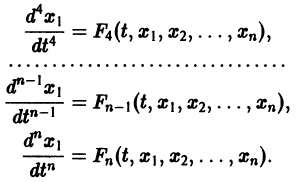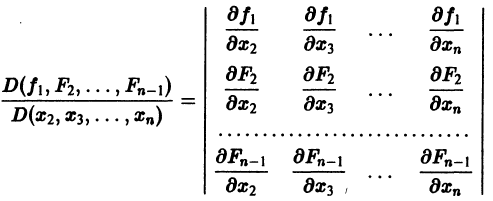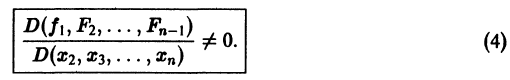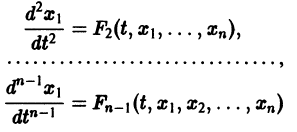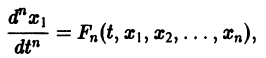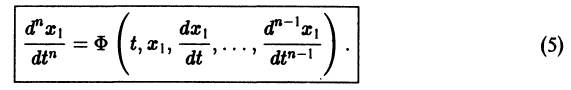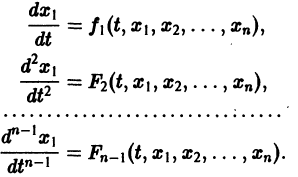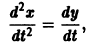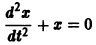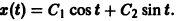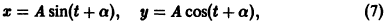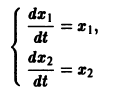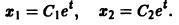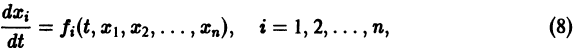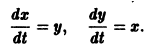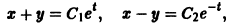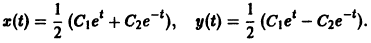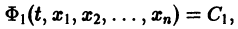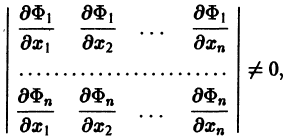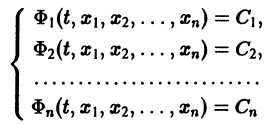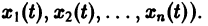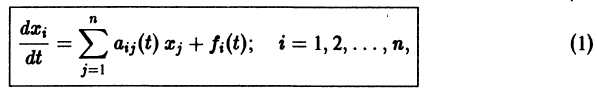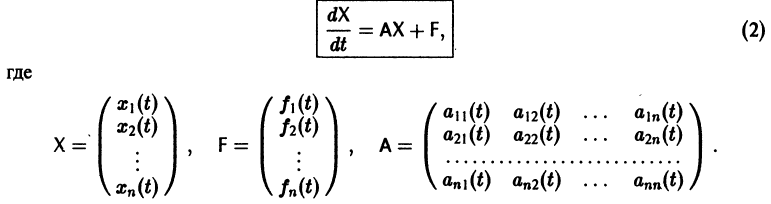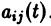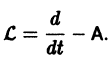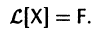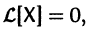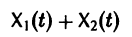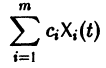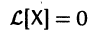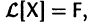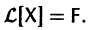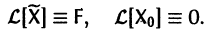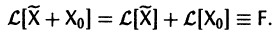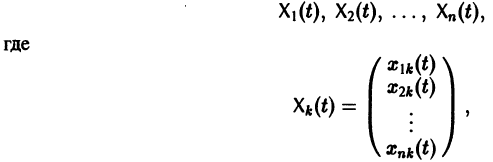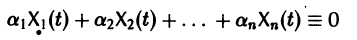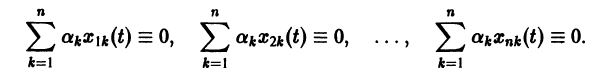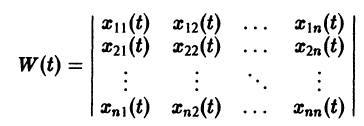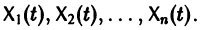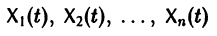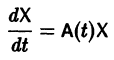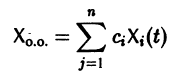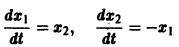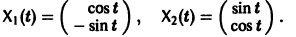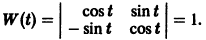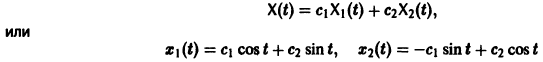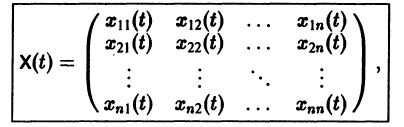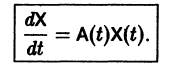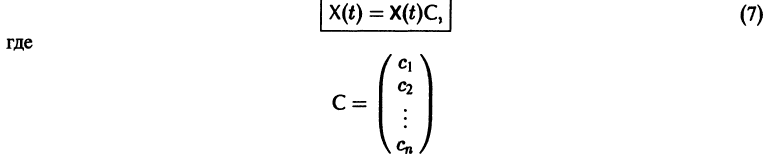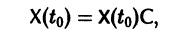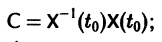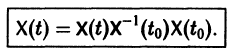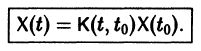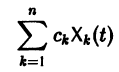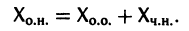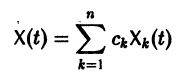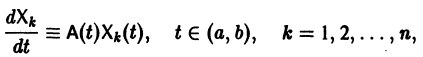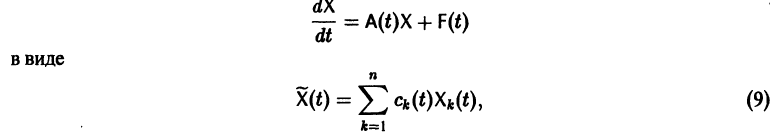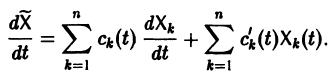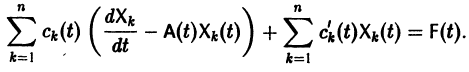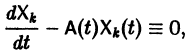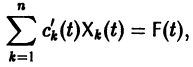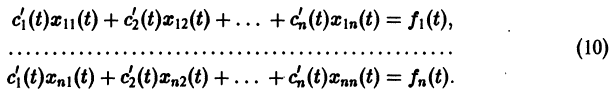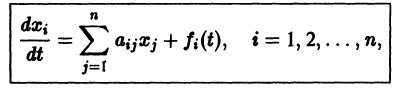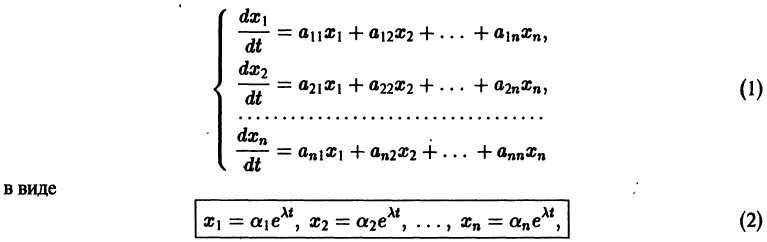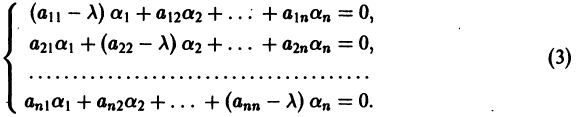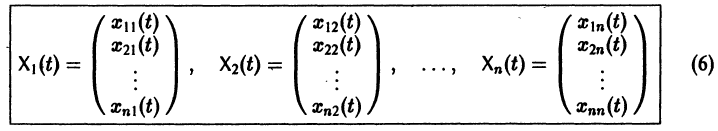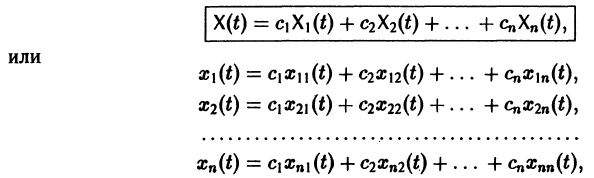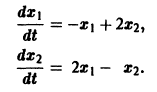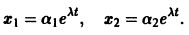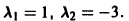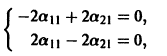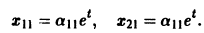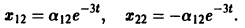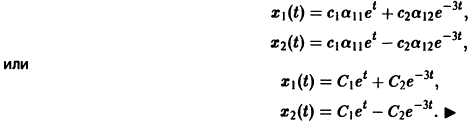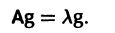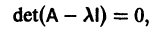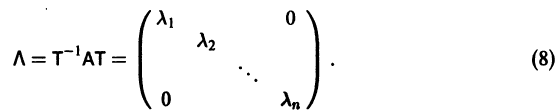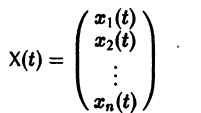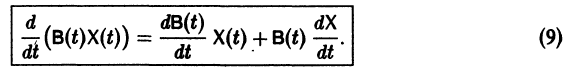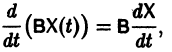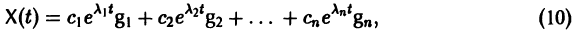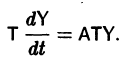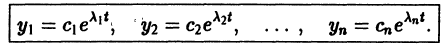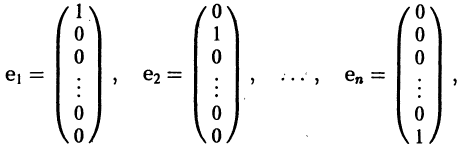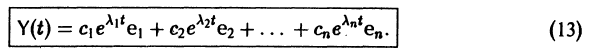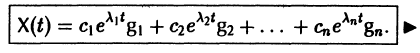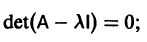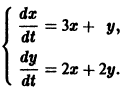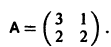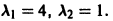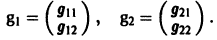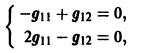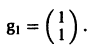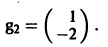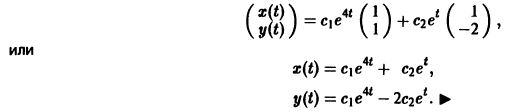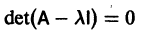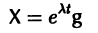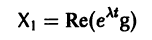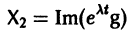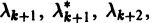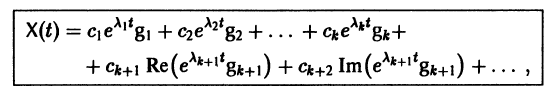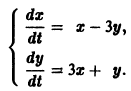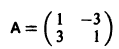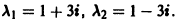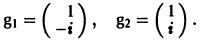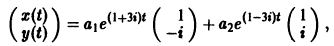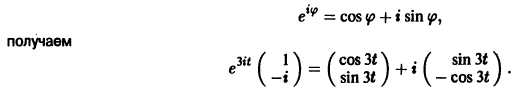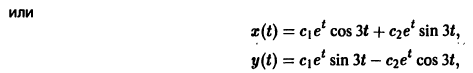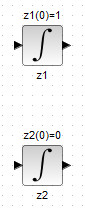Моделирование динамических систем: введение в GNU Octave
Жили-были умные, но очень жадные люди, которые написали замечательную программу Matlab. Умные они были потому, что программа вышла хорошей, а жадными, потому что очень любили деньги. Так любили, что брали их за свой Matlab не только с дядек серьезных, матлабом деньги зарабатывающих, а и с бедных студентов тоже, которым порой и сухую корочку хлеба купить не за что было. И кончилась бы сказочка скоро и невесело, если бы мир был не без добрых и умных людей, написавших похожие на матлаб программы, хоть худо-бедно работающие, да для всех желающих бесплатные. И с открытыми исходными текстами. Так что сами бедные студенты стали те программы дописывать, и работать они лучше и лучше стали с каждым годом. И стали тогда все жить-поживать, да добра наживать.
Введение
Большинство научных работников не ломают голову над тем, как устроены численные методы внутри. Они просто используют их, применяя в своей работе специализированные пакеты численных расчетов. Это совершенно не означает, что не нужно разбираться с тем, как эти методы устроены. Программу пишет человек, а ему свойственно ошибаться. И ошибки сквозят даже в самых дорогих и навороченных системах численной математики сплошь и рядом. К тому же есть задачи, где применение стандартных систем невозможно.
Вместе с тем, умение использовать универсальный математический софт это must have для современного ученого, потому что изобретая велосипед можно никогда не добраться до решения своей основной задачи. Сегодня мы рассмотрим обещанный Octave, попытавшись решить с его помощью очередную детскую задачу, сделав при этом недетские выводы.
1. Что такое Octave и где его взять
GNU Octave — свободный математический пакет численной математики, основанный на концепциях своего проприетарного собрата Matlab. Он доступен для всех популярных на сегодняшний день десктопных платформ, и получить его можно, зайдя в раздел загрузки на официальном сайте.
Большую часть экрана занимает так называемое командное окно, с приглашием командной строки вида «>>». Введем туда что нибудь и нажмем Enter
шикарно, переменная ans содержит результат последней операции, если вы явно не завели переменную под результат, например так
переменные вводятся «на ходу», как это принято в интерпретируемых языках. Да собственно m-язык октава и есть язык интерпретатора, очень напоминающий аналогичный язык матлаба. Один раз заведенная переменная сохраняет свое значение и тип до следующего присваивания, либо до полной очистки памяти командной оболочки
С левой стороны окна есть область, в которой расположены (сверху вниз): файловый менеджер, список глобальных переменных с их значениями, а также история введенных команд
Стоит обратить внимание на то, что для переменных указана размерность (Dimention) 1х1. Основным типом данных в Octave, как и в Matlab является матрица. Так вот наши числа это на самом деле матрицы размером 1 на 1 элемент.
Очистить все глобальные переменные можно выбрав в меню Edit -> Clear Workspace, а очистить командное окно — щелкнуть по нему правой кнопкой, выбрав Clear Window. Выполним очистку переменных и введя x получим
видно, что переменная x стала недоступна, до тех пока мы явно не присвоили ей значение снова.
Скажу честно, что с Ocatve я никогда не работал и разбираюсь вместе с читателем. Поэтому, предположим, что мы уже знаем достаточно, чтобы решить какую нибудь задачу. Например ту, которую решали в прошлый раз. Но сначала…
2. Нормальная форма Коши
и получаем вместо одного уравнения 2-го порядка два уравнения 1-го порядка, которые нужно решать вместе, одновременно
Это уже не одно уравнение, а система дифференциальных уравнений, содержащая две неизвестные зависимости 
и 
.
Как решать систему уравнений численно? Да так же, как и одно уравнение. Соберем все наши переменные в вектор-столбец (или массив, или матрицу-столбец, кому как удобно выражаться это не важно)
и правые части тоже соберем в вектор-столбец
Тогда рекуррентная формула метода Эйлера будет справедлива для каждого элемента этих столбцов
где n — число уравнений, в нашем случае их два.
К чему я всё это? А к тому, что Octave требует представлять дифференциальные уравнения именно в нормальной форме Коши.
С точки зрения механики вектор-столбец y называется вектором состояния системы или вектором фазовых координат. Тогда наша система уравнений превращается в одно векторное уравнение
Теперь возьмем, и в командном окне Octave наберем
Таким образом мы определяем функцию, которая на вход принимает текущее значение фазовых координат y и текущее время t, а на выходе возвращает значение производных от фазовых координат. Видим, что приглашение командной строки «>>» пропало, система ждет что мы закончим ввод тела функции ключевым словом endfunction. Продолжим набирать функцию
Итак, в теле функции мы определили g = 10 — принятое нами значение ускорения свободного падения. Мы видим, что же не появилось в списке переменных слева — эта переменная является локальной, и существует лишь в пределах функции. Переменная y это матрица-столбец, первый элемент y(1) которой это координата z, второй y(2) — проекция вектора скорости vz. Соответственно, dydt — это то значение, которое возвращает наша функция, это тоже матрица-столбец первый элемент которой это производная от z по времени, а второй — производная от vz по времени. То есть мы записали нашу систему дифференциальных уравнений в терминах Octave.
Теперь определимся с диапазоном времени, для которого нам надо получить результат. Пусть это будет десять точек от 0 до 1 секунды, с шагом 0.1 — сравним результат с ручным примером
Тут всё очевидно: t0 — начальный момент времени, tend — конечный момент времени. А вот deltaT = 0.1 секунда — это не шаг интегрирования! Это интервал, с которым Ocatve будет отображать для нас численное решение уравнения. Последняя команда формирует массив моментов времени для которых мы хотим получить решение.
Как вы знаете из прошлой статьи, для решения уравнения численно необходимо знать начальные значения скорости и координаты. Необходимо задать их для Octave
тем самым мы определили матрицу-столбец, содержащую начальную координату и начальное значение вертикальной проекции скорости. А теперь решаем уравнение
Функция lsode решит для нас уравнение численно. Первый параметр — имя функции, которая вычисляет производные от фазовых координат. Это функция F, мы её задали. Второй параметр — начальные условия, то есть значения фазовых координат в момент времени t = t0. Последний параметр — массив моментов времени, для которых мы хотим рассчитать значения фазовых координат. Жмем Enter…
В ответ вываливается гора требухи, оканчивающаяся предложением
нам предлагают листать требуху дальше (f), вернуться назад (b), или выйти (q). Те, кто знает *nix-подобные системы, знают, что это консольный вывод под управлением юниксовой утилиты less. Мы притворимся что не знаем, выйдем отсюда, нажав на клавиатуре q.
Наберем теперь в командной строке «y» и нажмем Enter
Ничего не напоминает? Ну конечно же это то самое решение, что мы получили для задачи из прошлой статьи. Только оно теперь удивительно точное — значения совпадают с аналитическим решением! Открою вам тайну — это точное решение нашей задачи. Связано это с тем, что функция lsode использует для решения задачи отнюдь не метод Эйлера, а нечто более продвинутое. Движение камня происходит с постоянным ускорением, и та формула численной аппроксимации, что применяется в данном методе, очевидно просто совпадает с аналитическим решением задачи. Хотя, если лезть в дебри представления машиной чисел с плавающей запятой, то… А ну да ладно, сейчас не об этом.
3. Строим график
Наберите теперь команду
Выскочит окошко с графическим представлением решения
Синяя кривая сверху — координата камня. Оранжевая снизу — вертикальная проекция скорости. Введенная команда неудобна тем, что строит график для всех функций сразу. А если мы хотим, построить, зависимость скорости от высоты? Тогда поступим так
Будет построен график, где по оси абсцисс пойдет переменная y(1), а по оси ординат — y(2), что есть соответственно высота и вертикальная проекция скорости
Такой график в механике называют фазовым портретом системы, то есть траекторией движения системы в пространстве фазовых координат. В данном случае фазовые координаты это высота камня над поверхностью Земли и его скорость. В механике часто нельзя получить точного решения в виде функций времени, но можно связать между собой координаты и скорости исходя из энергетических соображений. По полученным зависимостям можно найти фазовую траекторию системы и сделать много выводов о характере её движения не решая задачу до конца. Об этом мы тоже как-нибудь поговорим.
А пока предлагаю выполнить самостоятельное задание — постройте график зависимости высоты от времени и скорости от времени в отдельных окнах. И старайтесь не смотреть под спойлер
Заключение
На этом первое знакомство с Octave, как средой для численного моделирования будем считать оконченным. Теперь у нас есть мощный инструмент, с помощью которого мы будем постигать более изощренные премудрости.
Системы дифференциальных уравнений с примерами решения и образцами выполнения
Также как и обыкновенные дифференциальные уравнения, системы дифференциальных уравнений применяются для описания многих процессов реальной действительности. В частности, к ним относятся различного рода физические и химические процессы, процессы нефте- и газодобычи, геологии, экономики и т.д. Действительно, если некоторые физические величины (перемещение тела, пластовое давление жидкости в фиксированной точке с тремя координатами, концентрация веществ, объемы продаж продуктов) оказываются меняющимися со временем под воздействием тех или иных факторов, то, как правило, закон их изменения по времени описывается именно системой дифференциальных уравнений, т.е. системой, связывающей исходные переменные как функции времени и производные этих функций. Независимой переменной в системе дифференциальных уравнений может выступать не только время, но и другие физические величины: координата, цена продукта и т.д.
Решение систем дифференциальных уравнений
К системе дифференциальных уравнений приводит уже простейшая задача динамики точки: даны силы, действующие на материальную точку; найти закон движения, т. е. найти функции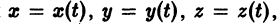 
выражающие зависимость координат движущейся точки от времени. Система, которая при этом получается, в общем случае имеет вид
Здесь x, у, z — координаты движущейся точки, t — время, f, g, h — известные функции своих аргументов.
Система вида (1) называется канонической. Обращаясь к общему случаю системы т дифференциальных уравнений с т неизвестными функциями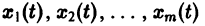 
аргумента t, назовем канонической систему вида
разрешенную относительно старших производных. Система уравнений первого порядка, разрешенных относительно производных от искомых функций,
Если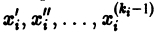 
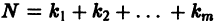
в (2) принять за новые вспомогательные функции, то общую каноническую систему (2) можно заменить эквивалентной ей нормальной системой, состоящей из 
уравнений. Поэтому достаточно рассматривать лишь нормальные системы.
Например, одно уравнение
является мастным случаем канонической системы. Положив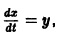 
в силу исходного уравнения будем иметь
В результате получаем нормальную систему уравнений
эквивалентную исходному уравнению.
Определение:
Решением нормальной системы (3) на интервале (а, Ь) изменения аргумента t называется всякая система n функций
дифференцируемых на интервале а 
Теорема:
Существования и единственности решения задачи Коши. Пусть имеем нормальную систему дифференциальных уравнений
и пусть функции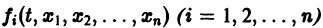 
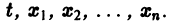
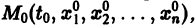
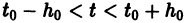
определены в некоторой (n + 1) — мерной области D изменения переменных 
Если существует окрестность 
точки 
в которой функции fi непрерывны по совокупности аргументов и имеют ограниченные частные производные по переменным 
то найдется интервал 
изменения t, на котором существует единственное решение нормальной системы (3), удовлетворяющее начальным условиям
Определение:
Система n функций
зависящих от t и n произвольных постоянных 
называется общим решением нормальной системы (3) в некоторой области существования и единственности решения задачи Коши, если
1) при любых допустимых значениях система функций (6) обращает уравнения (3) в тождества,
2) в области функции (6) решают любую задачу Коши.
Решения, получающиеся из общего при конкретных значениях постоянных называются частными решениями.
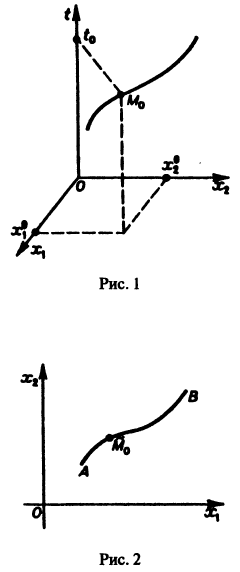
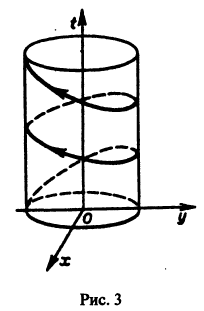
Обратимся для наглядности к нормальной системе двух уравнений,
Будем рассматривать систему значений t, x1, х2 как прямоугольные декартовы координаты точки трехмерного пространства, отнесенного к системе координат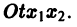 
Решение
системы (7), принимающее при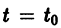 
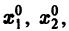
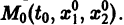
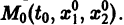
значения 
определяет в пространстве некоторую линию, проходящую через точку 
Эта линия называется интегральной кривой нормальной системы (7). Задача Коши для системы (7) получает следующую геометрическую формулировку: в пространстве переменных t, x1, х2 найти интегральную кривую, проходящую через данную точку (рис. 1). Теорема 1 устанавливает существование и единственность такой кривой.
Нормальной системе (7) и ее решению можно придать еще такое истолкование: будем независимую переменную t рассматривать как параметр, а решение
системы — как параметрические уравнения кривой на плоскости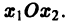 
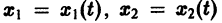
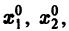
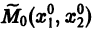
Эту плоскость переменных х1х2 называют фазовой плоскостью. В фазовой плоскости решение 
системы (7), принимающее при t = to начальные значения изображается кривой АВ, проходящей через точку 
(рис. 2). Эту кривую называют траекторией системы (фазовой траекторией). Траектория системы (7) есть проекция интегральной кривой на фазовую плоскость. По интегральной кривой фазовая траектория определяется однозначно, но не наоборот.
Методы интегрирования систем дифференциальных уравнений
Метод исключения
Один из методов интегрирования — метод исключения. Частным случаем канонической системы является одно уравнение n-го порядка, разрешенное относительно старшей производной
Введя новые функции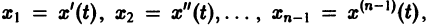 
заменим это уравнение следующей нормальной системой n уравнений:
т. е. одно уравнение n-го порядка эквивалентно нормальной системе (1)
Можно утверждать и обратное, что, вообще говоря, нормальная система п уравнений первого порядка эквивалентна одному уравнению порядка n. На этом и основан метод исключения для интегрирования систем дифференциальных уравнений.
Делается это так. Пусть имеем нормальную систему
Продифференцируем первое из уравнений (2) по t. Имеем
Заменяя в правой части производные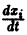 
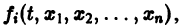
их выражениями 
получим
Уравнение (3) снова дифференцируем по t. Принимая во внимание систему (2), получим
Продолжая этот процесс, найдем
Предположим, что определитель
(якобиан системы функций 
отличен от нуля при рассматриваемых значениях 
Тогда система уравнений, составленная из первого уравнения системы (2) и уравнений
будет разрешима относительно неизвестных 
При этом выразятся через 
Внося найденные выражения в уравнение
получим одно уравнение n-го порядка
Из самого способа его построения следует, что если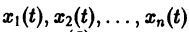 
есть решения системы (2), то функция х1(t) будет решением уравнения (5).
Обратно, пусть Х1(t) — решение уравнения (5). Дифференцируя это решение по t, вычислим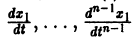 
и подставим найденные значения как известные функции
от t в систему уравнений
По предположению эту систему можно разрешить относительно т. е найти как функции от t.
Можно показать, что так построенная система функций
составляет решение системы дифференциальных уравнений (2). Пример:
Требуется проинтегрировать систему
Дифференцируя первое уравнение системы, имеем
откуда, используя второе уравнение, получаем
— линейное дифференциальное уравнение второго порядка с постоянными коэффициентами с одной неизвестной функцией. Его общее решение имеет вид
В силу первого уравнения системы находим функцию
Найденные функции x(t), y(t), как легко проверить, при любых значениях С1 и С2 удовлетворяют заданной системе.
Функции x(t), y(t) можно представить в виде
откуда видно, что интегральные кривые системы (6) — винтовые линии с шагом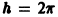 
и с общей осью х = у = 0, которая также является интегральной кривой (рис. 3).
Исключая в формулах (7) параметр t, получаем уравнение
так что фазовые траектории данной системы суть окружности с центром в начале координат — проекции винтовых линий на плоскость хОу.
При А = 0 фазовая траектория состоит из одной точки х = 0, у = 0, называемой точкой покоя системы.
Замечание:
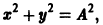
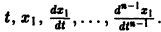
Может оказаться, что функции нельзя выразить через 
Тогда уравнения n-го порядка, эквивалентного исходной системе, мы не получим. Вот простой пример. Систему уравнений
нельзя заменить эквивалентным уравнением второго порядка относительно х1 или x2. Эта система составлена из пары уравнений 1-го порядка, каждое из которых интегрируется независимо, что дает
Метод интегрируемых комбинаций
Интегрирование нормальных систем дифференциальных уравнений
иногда осуществляется методом интегрируемых комбинаций.
Интегрируемой комбинацией называется дифференциальное уравнение, являющееся следствием уравнений (8), но уже легко интегрирующееся.
Пример:
Складывая почленно данные уравнения, находим одну интегрируемую комбинацию:
Вычитая почленно из первого уравнения системы второе, получаем вторую интегрируемую комбинацию:
Мы нашли два конечных уравнения
из которых легко определяется общее решение системы:
Одна интегрируемая комбинация дает возможность получить одно уравнение
связывающее независимую переменную t и неизвестные функции Такое конечное уравнение называется первым интегралом системы (8). Иначе: первым интегралом системы дифференциальных уравнений (8) называется дифференцируемая функция 
не равная тождественно постоянной, но сохраняющая постоянное значение на любой интегральной кривой этой системы.
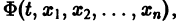
Если найдено п первых интегралов системы (8) и все они независимы, т. е. якобиан системы функций 
отличен от нуля:
то задача интефирования системы (8) решена (так как из системы
определяются все неизвестные функции 
Системы линейных дифференциальных уравнений
Система дифференциальных уравнений называется линейной, если она линейна относительно неизвестных функций и их производных, входящих в уравнение. Система n линейных уравнений первого порядка, записанная в нормальной форме, имеет вид
или, в матричной форме,
Теорема:
Если все функции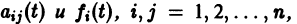 
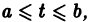
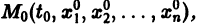
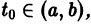
непрерывны на отрезке 
то в достаточно малой окрестности каждой точки 
где 
выполнены условия теоремы существования и единственности решения задачи Коши, следовательно, через каждую такую точку проходит единственная интегральная кривая системы (1).
Действительно, в таком случае правые части системы (1) непрерывны по совокупности аргументов t, и их частные производные по 
ограничены, так как эти производные равны непрерывным на отрезке [а,b] коэффициентам 
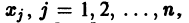
Введем линейный оператор
Тогда система (2) запишется в виде
Если матрица F — нулевая, т. е.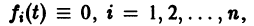 
на интервале (а,b), то система (2) называется линейной однородной и имеет вид
Приведем некоторые теоремы, устанавливающие свойства решений линейных систем.
Теорема:
Если X(t) является решением линейной однородной системы
то cX(t), где с — произвольная постоянная, является решением той же системы.
Теорема:
двух решений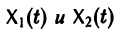 
однородной линейной системы уравнений является решением той же системы.
Следствие:
с произвольными постоянными коэффициентами сi решений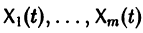 
линейной однородной системы дифференциальных уравнений
является решением той же системы.
Теорема:
Если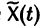 
есть решение линейной неоднородной системы
a Xo(t) — решение соответствующей однородной системы
будет решением неоднородной системы 
Действительно, по условию,
Пользуясь свойством аддитивности оператора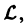 
получаем
Это означает, что сумма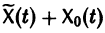 
есть решение неоднородной системы уравнений
Определение:
называются линейно зависимыми на интервале a 
при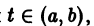 
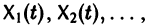
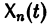
причем по крайней мере одно из чисел аi, не равно нулю. Если тождество (5) справедливо только при 
то векторы 
называются линейно независимыми на (а, b).
Заметим, что одно векторное тождество (5) эквивалентно n тождествам:
называется определителем Вронского системы векторов 
Определение:
Пусть имеем линейную однородную систему
где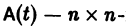 
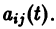
матрица с элементами 
Система n решений
линейной однородной системы (6), линейно независимых на интервале а 
с непрерывными на отрезке 
коэффициентами 
является линейная комбинация п линейно независимых на интервале а 
(
) — произвольные постоянные числа).
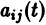
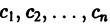
Пример:
имеет, как нетрудно проверить, решения
Эти решения линейно независимы, так как определитель Вронского отличен от нуля:
Общее решение системы имеет вид
(с1, с2 — произвольные постоянные).
Фундаментальная матрица
Квадратная матрица
столбцами которой являются линейно независимые решения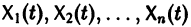 
системы (6), называется фундаментальной матрицей этой системы. Нетрудно проверить, что фундаментальная матрица удовлетворяет матричному уравнению
Если Х(t) — фундаментальная матрица системы (6), то общее решение системы можно представить в виде
— постоянная матрица-столбец с произвольными элементами. Полагая в (7) t = t0, имеем
Матрица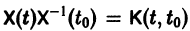 
называется матрицей Коши. С ее помощью решение системы (6) можно представить так:
Теорема:
О структуре общего решения линейной неоднородной системы дифференциальных уравнений. Общее решение в области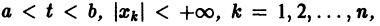 
линейной неоднородной системы дифференциальных уравнений
с непрерывными на отрезке коэффициентами aij(t) и правыми частями fi(t) равно сумме общего решения
соответствующей однородной системы и какого-нибудь частного решения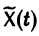 
неоднородной системы (2):
Метод вариации постоянных
Если известно общее решение линейной однородной системы (6), то частное решение неоднородной системы можно находить методом вариации постоянных (метод Лагранжа).
есть общее решение однородной системы (6), тогда
причем решения Xk(t) линейно независимы.
Будем искать частное решение неоднородной системы
где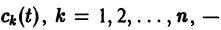 
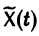
неизвестные функции от t. Дифференцируя по t, имеем
Подставляя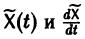 
в (2), получаем
то для определения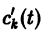 
получаем систему
или, в развернутом виде,
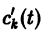
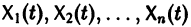
Система (10) есть линейная алгебраическая система относительно определителем которой является определитель Вронского W(t) фундаментальной системы решений . Этот определитель отличен от нуля всюду на интервале a 
где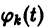 
— известные непрерывные функции. Интегрируя последние соотношения, находим
Подставляя эти значения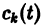 
в (9), находим частное решение системы (2)
(здесь под символом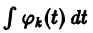 
понимается одна из первообразных для функции 
Системы линейных дифференциальных уравнений с постоянными коэффициентами
Рассмотрим линейную систему дифференциальных уравнений
в которой все коэффициенты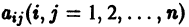 
— постоянные. Чаще всего такая система интегрируется сведением ее к одному уравнению более высокого порядка, причем это уравнение будет также линейным с постоянными коэффициентами. Другой эффективный метод интегрирования систем с постоянными коэффициентами — метод преобразования Лапласа.
Мы рассмотрим еще метод Эйлера интегрирования линейных однородных систем дифференциальных уравнений с постоянными коэффициентами. Он состоит в следующем.
Метод Эйлера
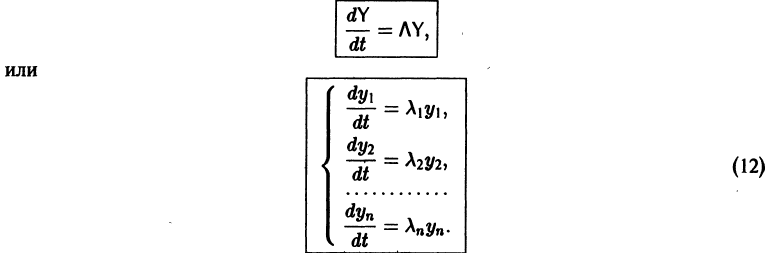
Будем искать решение системы
где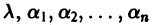 
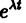
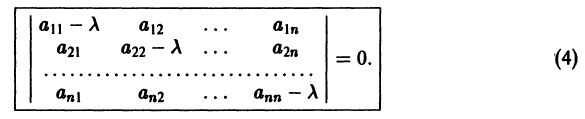
— постоянные. Подставляя Xk в форме (2) в систему (1), сокращая на 
и перенося все члены в одну часть равенства, получаем систему
Для того, чтобы эта система (3) линейных однородных алгебраических уравнений с n неизвестными 
имела нетривиальное решение, необходимо и достаточно, чтобы ее определитель был равен нулю:
Уравнение (4) называется характеристическим. В его левой части стоит многочлен относительно 
степени n. Из этого уравнения определяются те значения , при которых система (3) имеет нетривиальные решения . Если все корни 
характеристического уравнения (4) различны, то, подставляя их по очереди в систему (3), находим соответствующие им нетривиальные решения 
этой системы n, следовательно, находим п решений исходной системы дифференциальных уравнений (1) в виде
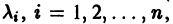
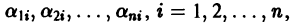
где второй индекс указывает номер решения, а первый — номер неизвестной функции. Построенные таким образом п частных решений линейной однородной системы (1)
образуют, как можно проверить, фундаментальную систему решений этой системы.
Следовательно, общее решение однородной системы дифференциальных уравнений (1) имеет вид
где 
произвольные постоянные.
Случай, когда характеристическое уравнение имеет кратные корни, мы рассматривать не будем.
Пример:
Ищем решение в виде
имеет корни 
Система (3) для определения a1, а2 выглядит так:
Подставляя в (*)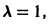 
получаем
откуда а21 = а11. Следовательно,
Полагая в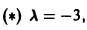 
находим a22 = — a12, поэтому
Общее решение данной системы:
Матричный метод
Изложим еще матричный метод интегрирования однородной системы (1). Запишем систему (1) в виде
матрица с постоянными действительными элементами 
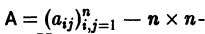
Напомним некоторые понятия из линейной алгебры. Вектор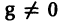 
называется собственным вектором матрицы А, если
Число называется собственным значением матрицы А, отвечающим собственному вектору g, и является корнем характеристического уравнения
где I — единичная матрица.
Будем предполагать, что все собственные значения 
матрицы А различны. В этом случае собственные векторы g1, g2, …gn линейно независимы и существует 
матрица Т, приводящая матрицу А к диагональному виду, т. е. такая, что
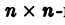
Столбцами матрицы Т являются координаты собственных векторов g1, g2 …, gn матрицы А.
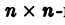
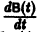
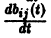
Введем еще следующие понятия. Пусть В(t) — матрица, элементы 
которой суть функции аргумента t, определенные на множестве . Матрица В(t) называется непрерывной на 
, если непрерывны на все ее элементы . Матрица В(t) называется дифференцируемой на , если дифференцируемы на все элементы этой матрицы. При этом производной матрицы 
называется матрица, элементами которой являются производные 
у соответствующих элементов матрицы В(t).
Пусть B(t) — n х n-матрица,
— вектор-столбец. Учитывая правила алгебры матриц, непосредственной проверкой убеждаемся в справедливости формулы
В частности, если В — постоянная матрица, то
так как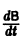 
есть нуль-матрица.
Теорема:
Если собственные значения матрицы А различны, то общее решение системы (7) имеет вид
где g1, g2,…, gn — собственные векторы-столбцы матрицы А, 
произвольные постоянные числа.
Введем новый неизвестный вектор-столбец Y(t) по формуле
где Т — матрица, приводящая матрицу А к диагональному виду. Подставляя X(t) из (11) в (7), получим систему
Умножая обе части последнего соотношения слева на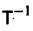 
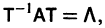
и учитывая, что 
придем к системе
Мы получили систему из n независимых уравнений, которая без труда интегрируется:
Здесь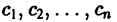 
— произвольные постоянные числа.
Вводя единичные n-мерные векторы-столбцы
решение Y(t) можно представить в виде
В силу (11) Х(t) = TY(t). Так как столбцы матрицы Т есть собственные векторы матрицы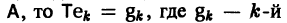 
собственный вектор матрицы А. Поэтому, подставляя (13) в (11), получим формулу (10):
Таким образом, если матрица А системы дифференциальных уравнений (7) имеет различные собственные значения, для получения общего решения этой системы:
1) находим собственные значения матрицы как корни алгебраического уравнения
2) находим все собственные векторы g1, g2,…, gn;
3) выписываем общее решение системы дифференциальных уравнений (7) по формуле (10).
Пример:
Матрица А системы имеет вид
1) Составляем характеристическое уравнение
Корни характеристического уравнения 
2) Находим собственные векторы
Для = 4 получаем систему
откуда g11 = g12, так что
Аналогично для = 1 находим
3) Пользуясь формулой (10), получаем общее решение системы дифференциальных уравнений
Корни характеристического уравнения могут быть действительными и комплексными. Так как по предположению коэффициенты 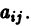системы (7) действительные, то характеристическое уравнение
будет иметь действительные коэффициенты. Поэтому наряду с комплексным корнем оно будет иметь и корень *, комплексно сопряженный с . Нетрудно показать, что если g — собственный вектор, отвечающий собственному значению , то * — тоже собственное значение, которому отвечает собственный вектор g*, комплексно сопряженный с g.
При комплексном решение
системы (7) также будет комплексным. Действительная часть
этого решения являются решениями системы (7). Собственному значению * будет отвечать пара действительных решений X1 и -Х2, т. е. та же пара, что и для собственного значения . Таким образом, паре , * комплексно сопряженных собственных значений отвечает пара действительных решений системы (7) дифференциальных уравнений.
Пусть 
— действительные собственные значения, 
— комплексные собственные значения. Тогда всякое действительное решение системы (7) имеет вид
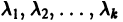
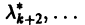
где сi — произвольные постоянные.
Пример:
1) Характеристическое уравнение системы
Его корни 
2) Собственные векторы матриц
3) Решение системы
где а1, а2 — произвольные комплексные постоянные.
Найдем действительные решения системы. Пользуясь формулой Эйлера
Следовательно, всякое действительное решение системы имеет
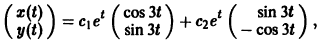
где с1, с2 — произвольные действительные числа.
Понятие о системах дифференциальных уравнений
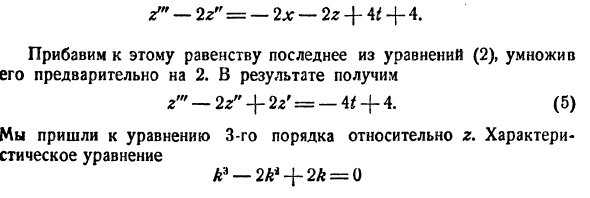
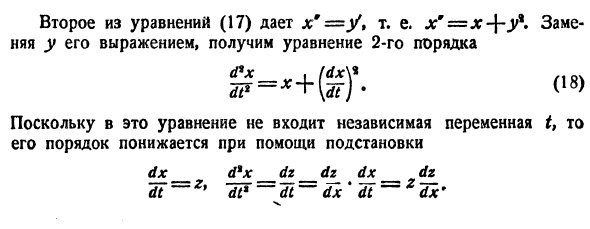
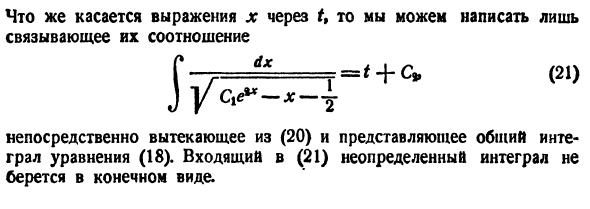
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Сведение к системе дифференциального уравнения 2-ой степени в Xcos
Способ 2: сведение к системе в форме Коши
Рассмотрим более привычный и распространённый способ численного интегрирования обыкновенных дифференциальных уравнений n-го порядка: сведение к системе из n уравнений 1-го порядка, или, как ещё говорят, к нормальной форме или форме Коши.
Решение систем ОДУ без использования визульных блоков, было рассмотрено ранее в материале.
Рассмотрим дифференциальное уравнение второго порядка с заданными начальными условиями:
Введём замену переменных, сводящих уравнение (1) к системе из двух уравнений первой степени:
\begin
получим систему в новых фазовых переменных
(2)\begin
Данную систему нам и необходимо замоделировать. Итак, разберём, какие из функциональных бликов Xcos понадобятся, чтобы найти решение задачи Коши системы из двух дифференциальных уравнений 1-ой степени (2) с начальными условиями (3).
Система (2) содержит два д.у. первого порядка, а значит нам понадобятся два блока интегратора. Здесь и в дальнейшем для моделирования дифференциальных уравнений, вместо INTEGRAL_f, будем использовать блок 
с палитры «Системы с непрерывным временем». Смысловая нагрузка у блока INTEGRAL_m та же, что и у используемого ранее INTEGRAL_f, — поиск первообразной сигнала, подающегося на его вход. Однако блок INTEGRAL_m во-первых, более нагляден, а во-вторых, имеет большее количество настраиваемых внутренних параметров блока.
Итак, приступим к сбору функциональной блок-схемы, реализующей поиск численного решения системы дифференциальных уравнений (2), удовлетворяющего начальным условиям (3). Для создания блок-схемы нам потребуется:
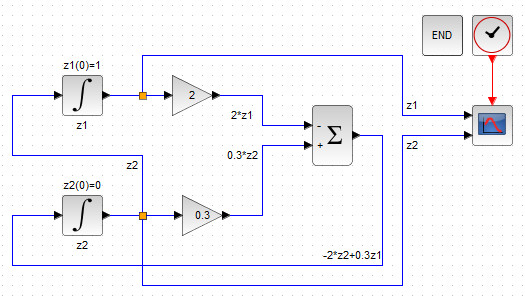
Добавить два блока INTEGRAL_m на рабочую область, дав им названия соответствующих фазовых переменных и задать во внутренних параметрах блоков INTEGRAL_m значения параметра Initial condition (начальные условия), указанные в (7б). Результатом данных действий будет схема, изображенная на рис.38;
Рисунок 38. Блоки интеграторов с заданными начальными условиями
Собирать уравнения системы (2) необходимо, начиная с последнего и двигаясь вверх. Второе уравнение системы (2) имеет вид \(z_2′ = -2z_2+0.3z_1 \)и представляет собой сумму двух слагаемых с разными знаками, первое из которых увеличено в 2 раза, а второе в 0.3 раз.
Поэтому нам потребуется добавить блок сумматора BIGSOM_f, во внутренних параметрах которого указан знаков слагаемых [-1;1] и блоки усилителя GAINBLK_f со значениями 2 и 3 соответственно.
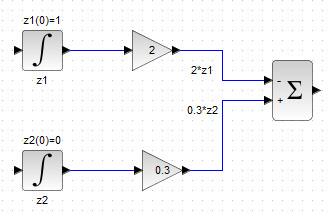
Далее необходимо составить правую част рассматриваемого уравнения, то есть подать на вход BIGSOM_f, советующие слагаемые, как показано на рис. 39.
Рисунок 39. Блок-схема правой части второго диф.уравнения системы (2)
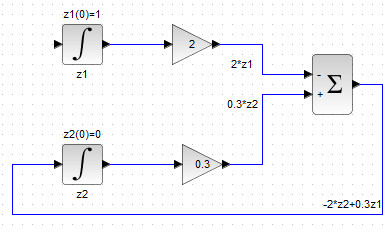
Итак, мы получили в сумматоре выражение, которые необходимо проинтегрировать, то есть подать на вход блока-интегратора INTEGRAL_m , соответствующего фазовой переменной, производная которой стоит в левой части рассматриваемого уравнения. В уравнении \(z_2′ = -2z_2+0.3z_1 \) слева стоит \(z_2′ \), а значит, выход сумматора нужно подсоединить ко входу интегратора, отвечающего за переменную \(z_2 \)(см. рис. 40).
Рисунок 40. Вывод выхода сумматора на вход интегратора
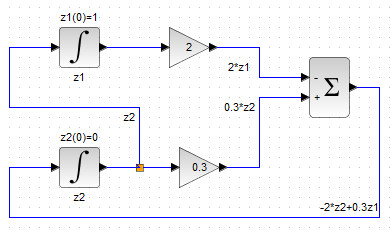
Перейдём к построению первого уравнения системы (2), имеющего вид \(z_1’=z_2 \). Фазовая переменная \(z_2 \) формируется как выход соответствующего блока интегратора. Распараллелим выход нижнего блока INTEGRAL_m , подав его на вход верхнего блока INTEGRAL_m , который соответствует фазовой переменной \(z_1 \). В результате получим схему, изображенную на рисунке 41.
Рисунок 41. Блок-схема замкнутой системы двух д.у. 1-ой степени (2)
Далее нам потребуется вывести графики фазовых переменных \(z_1, z_2 \), для этого добавьте блоки CMSCOPE, END и CLOCK_c на рабочую область.
По традиции, во внутренних параметрах блока END указать время 10сек., на функциональный вход блока CMSCOPE нужно подать выход блока CLOCK_c с параметрами Period = 0.1, Время инициализации=0, а на регулярные входы осциллографа подать распараллеленные интегральные выходы, соответствующие фазовым переменным (рис. 42).
Рисунок 42. Блок-схема поиска численного задачи Коши (2-3) с выводом графиков фазовых переменных
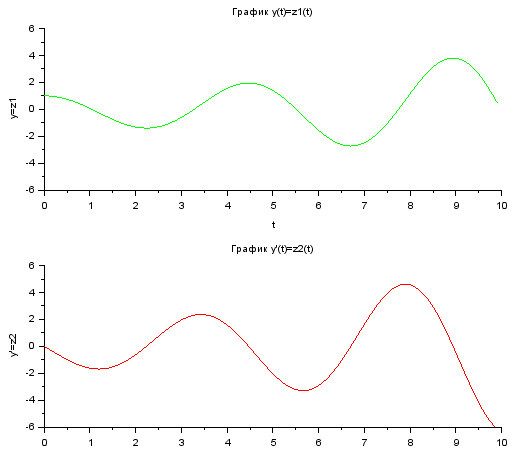
После запуска моделирования и настройки параметров осциллографа, получим графики (рис. 43).
Рисунок 43. Графическое решение задачи Коши (2-3)
Итак, основными принципами второго способа численного интегрирования дифференциальных уравнений порядка выше 1 являются:
Сведение дифференциального уравнения n-ой к системе из n уравнений 1-ой степени, путём замены переменных;
Движение снизу вверх при визуализации уравнений получившейся системы;
Параллельное включение в схему блоков INTEGRAL_m, отвечающих за фазовые переменные системы;
Отображение результата численного моделирования на системах координат фазовая переменная – время;
Задание начальных условий в соответствующих блоках-интеграторах;
Задание отрезка интегрирования во внутренних параметрах блока END, начальной точки и шага дискретизации в блоке CLOCK_c;
Возможность выбора численного метода поиска решения дифференциального уравнения в настройкам параметров интегрирования.
http://lfirmal.com/ponyatie-o-sistemah-differencialnyh-uravnenij/
http://inclab.ru/xcos/svedenie-k-sisteme-v-forme-koshi