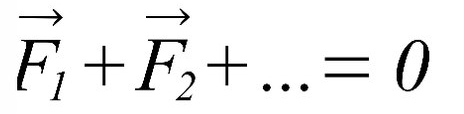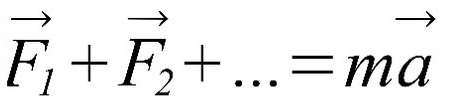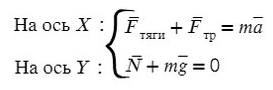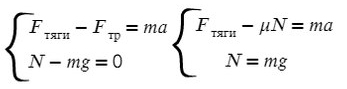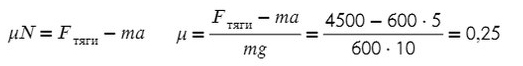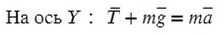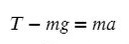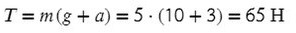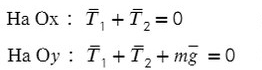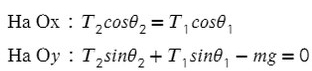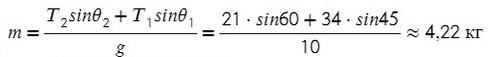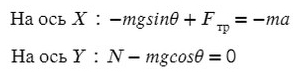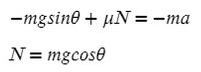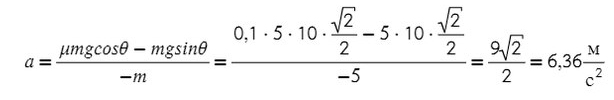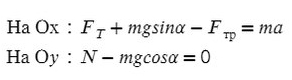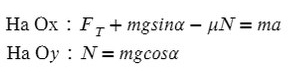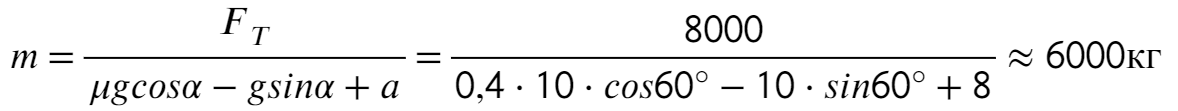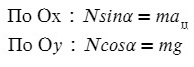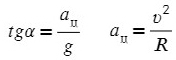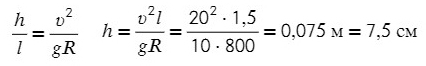Система уравнения на ось x

Система уравнения на ось x

Задачи по динамике.

I и II закон Ньютона.

Ввод и направление осей.

Проецирование сил на оси.

Решение систем уравнений.

Самые типовые задачи по динамике

Начнем с I и II законов Ньютона.

Откроем учебник физики и прочтем. I закон Ньютона: существуют такие инерциальные системы отсчета в которых. Закроем такой учебник, я тоже не понимаю. Ладно шучу, понимаю, но объясню проще.

I закон Ньютона: если тело стоит на месте либо движется равномерно (без ускорения), сумма действующих на него сил равна нулю.

Вывод: Если тело движется с постоянной скоростью или стоит на месте векторная сумма сил будет ноль.

II закон Ньютона: если тело движется равноускоренно или равнозамедленно (с ускорением), сумма сил, действующих на него, равна произведению массы на ускорение.

Вывод: Если тело двигается с изменяющейся скоростью, то векторная сумма сил, которые как-то влияют на это тело ( сила тяги, сила трения, сила сопротивления воздуха), равна массе этого тело умножить на ускорение.

При этом одно и то же тело чаще всего движется по-разному (равномерно или с ускорением) в разных осях. Рассмотрим именно такой пример.

Задача 1. Определите коэффициент трения шин автомобиля массой 600 кг, если сила тяги двигателя 4500 Н вызывает ускорение 5 м/с².

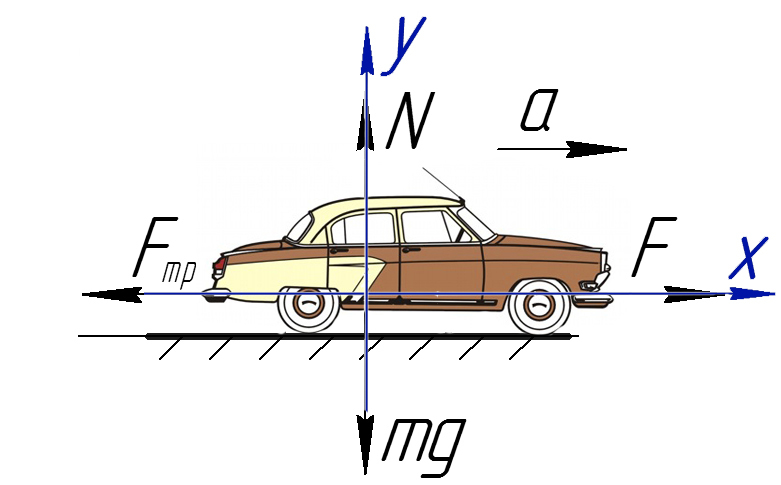
Обязательно в таких задачах делать рисунок, и показывать силы, которые дествуют на машину:

На Ось Х: движение с ускорением

На Ось Y: нет движения (здесь координата, как была ноль так и останется, машина не поднимает в горы или спускается вниз)

Те силы, направление которых совпадает с направлением осей, будут с плюсом, в противоположном случае — с минусом.

По оси X: сила тяги направлена вправо, так же как и ось X, ускорение так же направлено вправо.

Fтр = μN, где N — сила реакции опоры. На оси Y: N = mg, тогда в данной задаче Fтр = μmg.

Коэффициент трения — безразмерная величина. Следовательно, единиц измерения нет.

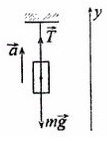
Задача 2. Груз массой 5кг, привязанный к невесомой нерастяжимой нити, поднимают вверх с ускорением 3м/с². Определите силу натяжения нити.

Сделаем рисунок, покажем силы, которые дествуют на груз

T — сила натяжения нити

На ось X: нет сил

Разберемся с направлением сил на ось Y:

Выразим T (силу натяжения) и подставим числительные значения:

Самое главное не запутаться с направлением сил (по оси или против), все остальное сделает калькулятор или всеми любимый столбик.

Далеко не всегда все силы, действующие на тело, направлены вдоль осей.

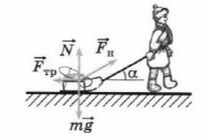
Простой пример: мальчик тянет санки

Если мы так же построим оси X и Y, то сила натяжения (тяги) не будет лежать ни на одной из осей.

Чтобы спроецировать силу тяги на оси, вспомним прямоугольный треугольник.

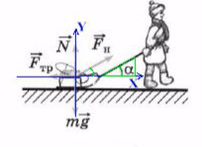
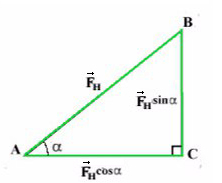
Отношение противолежащего катета к гипотенузе — это синус.

Отношение прилежащего катета к гипотенузе — это косинус.

Сила тяги на ось Y — отрезок (вектор) BC.

Сила тяги на ось X — отрезок (вектор) AC.

Если это непонятно, посмотрите задачу №4.

Чем длинее будет верека и, соответсвенно, меньше угол α, тем проще будет тянуть санки. Идеальный вариант, когда веревка параллельна земле , ведь сила, которая действуют на ось X— это Fнcosα. При каком угле косинус максимален? Чем больше будет этот катет, тем сильнее горизонтальная сила.

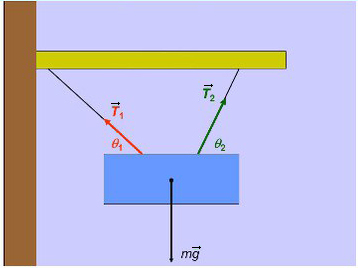
Задача 3. Брусок подвешен на двух нитях. Сила натяжения первой составляет 34 Н, второй — 21Н, θ1 = 45°, θ2 = 60°. Найдите массу бруска.

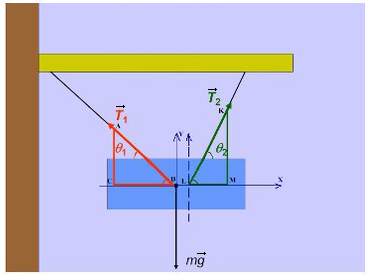
Введем оси и спроецируем силы:

Получаем два прямоугольных треугольника. Гипотенузы AB и KL — силы натяжения. LM и BC — проекции на ось X, AC и KM — на ось Y.

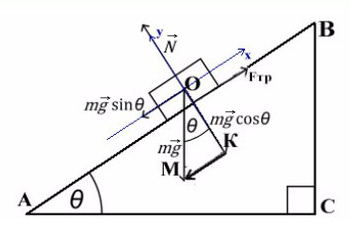
Задача 4. Брусок массой 5 кг (масса в этой задаче не нужна, но, чтобы в уравнениях все было известно, возьмем конкретное значение) соскальзывает с плоскости, которая наклонена под углом 45°, с коэффициентом трения μ = 0,1. Найдите ускорение движения бруска?

Когда же есть наклонная плоскость, оси (X и Y) лучше всего направить по направлению движения тела. Некоторые силы в данном случае ( здесь это mg) не будут лежать ни на одной из осей. Эту силу нужно спроецировать, чтобы она имела такое же направление, как и взятые оси.
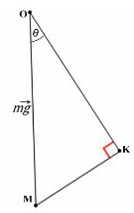
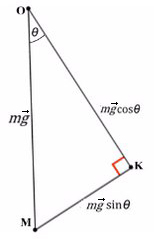
Всегда ΔABC подобен ΔKOM в таких задачах (по прямому углу и углу наклона плоскости).

Рассмотрим поподробнее ΔKOM:

Получим, что KO лежит на оси Y, и проекция mg на ось Y будет с косинусом. А вектор MK коллинеарен (параллелен) оси X, проекция mg на ось X будет с синусом, и вектор МК направлен против оси X (то есть будет с минусом).

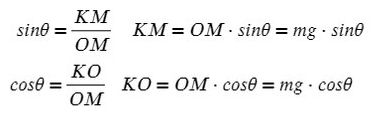
Не забываем, что, если направления оси и силы не совпадают, ее нужно взять с минусом!

Из оси Y выражаем N и подставляем в уравнение оси X, находим ускорение:

Как видно, массу в числителе можно вынести за скобки и сократить со знаменаталем. Тогда знать ее не обязательно, получить ответ реально и без нее.
Да-да, в идеальных условиях (когда нет силы сопротивления воздуха и т.п.), что перо, что гиря скатятся (упадут) за одно и тоже время.

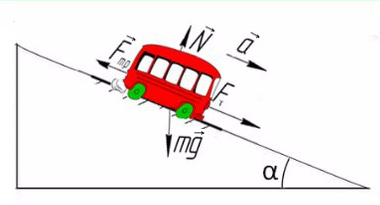
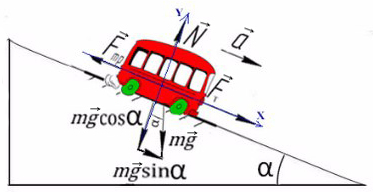
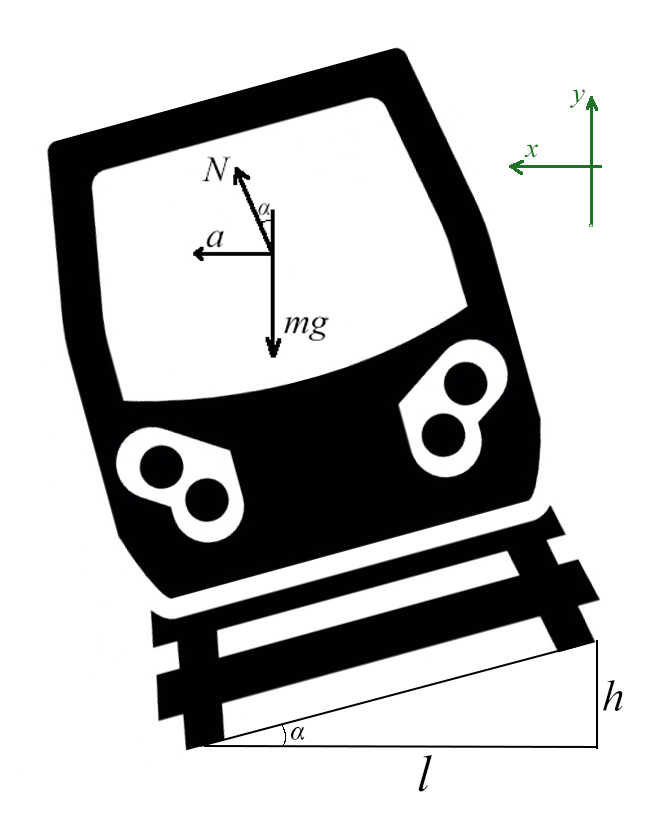
Задача 5. Автобус съезжает с горки под уклоном 60° с ускорением 8 м/с² и с силой тяги 8 кН. Коэффициент трения шин об асфальт равен 0,4. Найдите массу автобуса.

Сделаем рисунок с силами:

Введем оси X и Y. Спроецируем mg на оси:

Запишем второй закон Ньютона на X и Y:

Задача 6. Поезд движется по закруглению радиуса 800 м со скоростью 72 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего. Расстояние между рельсами 1,5 м.

Самое сложное — понять, какие силы куда действуют, и как угол влияет на них.

Вспомни, когда едешь по кругу на машине или в автобусе, куда тебя выталкивает? Для этого и нужен наклон, чтобы поезд не упал набок!

Угол α задает отношение разницы высоты рельсов к расстоянию между ними (если бы рельсы находились горизонтально)

Запишем какие силы действуют на оси:

Ускорение в данной задачи центростремительное!

Поделим одно уравнение на другое:

Тангенс — это отношение противолежащего катета к прилежащему:

Как мы выяснили, решение подобных задач сводится к расстановке направлений сил, проецированию их на оси и к решению систем уравнений, почти сущий пустяк.

В качестве закрепления материала решите несколько похожих задач с подсказками и ответами.

Плоская система сходящихся сил

Содержание:

Плоская система сходящихся сил – это система сил линии действия которых сходятся в одной точке, называются сходящимися.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Плоская система сходящихся сил — основные понятия и определения

Если все силы, приложенные к телу, расположенные в одной плоскости и линии их действия пересекаются в одной точке, то такая система сил носит название плоской системы сходящихся сил.

Покажем на рис. 1.6 произвольное тело, к которому приложена плоская системы сходящихся сил , , . . При этом линии действия всех сил пересекаются в точке A.

Определение равнодействующей системы сходящихся сил

Геометрический способ сложения сил:

Добавить систему сил означает определить их равнодействующую. Попробуем найти равнодействующую для плоской системы сходящихся сил, которая изображена на
рис. 1.6. Возьмем (условно) две первые силы и и на основании III аксиомы
статики найдем их равнодействующую , для чего на силах и , как на
сторонах, построим свой параллелограмм, диагональ которого, которая приложена в
точке A, и является их равнодействующей . Далее геометрически добавим две следующие силы и , и уже на этих силах как на сторонах построим свой
параллелограмм, диагональ которого будет второй равнодействующей . Так же дальше продолжаем до последней силы . Когда построено последний параллелограмм и проведена последняя диагональ, то она и будет равнодействующей системы сходящихся сил, которая показана на рис. 1.6

Если внимательно присмотреться к геометрическому построению параллелограммов, то можно увидеть, что к концу вектора силы был присоединен вектор силы (то есть в конец вектора перенесено параллельно вектор ) и так далее до последней силы .

Таким образом, геометрический способ добавления сходящихся сил сводится к построению силового многоугольника. Он строится путем параллельного переноса векторов сил в масштабе, когда начало следующей силы совпадает с концом предыдущей силы. Тогда вектор равнодействующей соединяет начало первой силы с концом последней силы. Это можно записать так:

Величина равнодействующей силы не изменится, если будет изменен порядок
присоединения (добавление) сил до многоугольника, но конфигурация силового
многоугольника будет другой.

Условие равновесия плоской системы сходящихся сил в геометрической форме

Если к свободному материальному телу приложена одна сила, то о равновесии этого тела речи не может быть. Таким образом, если рассматривать плоскую систему сходящихся сил, которая сведена к равнодействующей, то тело не может быть в равновесии.

Для равновесия тела под действием плоской системы сходящихся сил необходимо и
достаточно, чтобы равнодействующая всех сил была равна нулю.

Равнодействующая такой системы сил будет равна нулю, когда силовой многоугольник будет замкнутым, то есть когда начало вектора первой силы будет совпадать с концом вектора последней силы.

Теорема о равновесии тела под действием трех не параллельных сил

Если тело под действием системы трех плоских не параллельных сил находится в равновесии, то линии действия этих сил пересекаются в одной точке.

Представим тело (рис. 1.7), к которому в точках А, B, C приложены силы
, , , векторы которых расположены в одной плоскости. Рассмотрим сначала две силы и . На основании следствия из I и II аксиом статики указанные силы всегда можно перенести по линии их действия в одну точку, например, в точку О.

Далее, если есть в точке О две приложенные силы, то на основании III аксиомы статики их можно заменить одной силой, то есть равнодействующей . Построим на рис. 1.7 на указанных векторах сил и параллелограмм и покажем равнодействующую .Теперь тело находится под действием только двух сил и и оно будет в равновесии только тогда, когда векторы этих сил расположены на одной прямой, то есть на прямой CO. Тогда и вектор силы пересекает точку О. Теорема доказана.

Проекция силы на ось и на плоскость

Представим силу , вектор который произвольно расположен в плоскости чертежа (рис. 1.8). Выберем в этой плоскости ось, например, ось x. Необходимо спроектировать указанную силу на эту ось x.

Обозначим сначала конце вектора силы буквами А и В и опустим из них на ось x перпендикуляры. Точки пересечения перпендикуляров с осью x (обозначим их соответствующими строчными буквами а и в) образовали на оси x направленный отрезок, который и будет проекцией силы на ось x. По величине этот отрезок равен произведению модуля силы || на косинус угла, под которым вектор силы пересекает ось. А именно:

По знаку проекция силы на ось тогда будет положительная, когда угол α (угол пересечения направления вектора силы или линии действия силы с осью) острый. В полной мере разумеется, если этот угол равен в 90º, то проекция силы на ось x равна нулю. Если угол α будет тупой, то проекция силы на ось x будет иметь отрицательный знак. Значения проекции в данном случае будет

Но практически тут удобнее использовать тупой угол α₂, а острый угол β между вектором силы и направлением оси x. Знак проекции легко определяется из схемы

Таким образом, проекция силы на ось — это направленный отрезок на оси, образованный между перпендикулярами, которые опущены из концов вектора силы на ось, и который по величине равен произведению модуля силы на косинус угла между направлением вектора силы и осью.

Спроектируем теперь вектор силы на плоскость и оси координат.

Возьмем силу , вектор которой произвольно расположен в пространстве (рис. 1.9). Выберем в пространстве прямоугольную декартову систему координат Oxyz, начало отсчета которой (точка O) совмещенное с точкой приложения вектора силы . Спроектируем вектор силы на плоскость xOy. Опустим из точки А (конец вектора силы) на указанную плоскость перпендикуляр, который пересекает ее в точке а. На плоскости xOy создан вектор , который и является проекцией силы на плоскость. По модулю эта проекция равна

где α — угол между вектором силы и плоскостью xOy.

Следует заметить, что проекция вектора силы на плоскость является вектором, потому что плоскость на имеет базисных векторов, ортов.

Если в плоскости xOy обозначить угол β, то есть возможность спроектировать силу на оси x и y, опуская с точки a на оси перпендикуляры и по известному уже правилу получить проекции вектора на указанные оси:

В данном случае через ось z и вектор силы можно провести плоскость, поэтому есть возможность спроектировать силу на эту ось по известному правилу. Эта проекция будет равняться

где ϒ — угол между вектором силы и осью z.

Определение силы за ее проекциями

Предположим, что у нас в плоскости рисунка имеем прямоугольную декартову систему координат Oxy, заданные две проекции силы — и (рис. 1.10). Надо по данным проекциями вычислить модуль вектора самой силы , а также его направление.

На заданных проекциях, как на сторонах, строим прямоугольник, диагональ которого, проходит через точку пересечения проекций, и является искомым вектором силы . Модуль силы можно определить из следующего выражения:

Углы между вектором силы и осями x и y можно определить с помощью направляющих косинусов

Зная направляющие косинусы, через арккосинус есть возможность найти сами углы.

Аналогично для пространственной системы сил (рис. 1.9) можно построить на проекциях сила как на сторонах параллелепипед, а модуль силы определить так:

Направление вектора этой силы также определяется через направляющие косинусы его углов с соответствующими осями координат x, y и z:

Через арккосинус определяют сами углы.

Теорема о проекции равнодействующей силы на ось

Проекция вектора равнодействующей силы на ось равна алгебраической сумме проекций векторов составляющих сил на ту же ось.

Доказательство. Имеем систему сил , , , ,которая сведена к равнодействующей с помощью силового многоугольника (рис. 1.11). Введем на плоскости прямоугольную декартову систему координат Ox y и спроектируем на ось x все силы. Для этого обозначим концы векторов всех сил буквами — А, В, С, D, K и проведем перпендикуляры из каждой точки на ось x. Точки пересечения перпендикуляров с осью, которые обозначены соответствующими строчными буквами — а, в, с, d, k образовали на оси x направлены отрезки, которые и являются проекциями всех сил на эту ось. Каждая проекция, соответственно, равна

Добавим алгебраически все проекции и подсчитаем, почему эта сумма равна:

Но отрезок ak и является проекцией равнодействующей силы на ось x. Распространяя эту сумму на n сил, можно записать:

Аналитический способ добавления системы сходящихся сил

На основании теоремы о проекции равнодействующей силы на ось, имеем:

Аналогично проекция равнодействующей силы на ось y будет равняться

Модуль равнодействующей равен

Углы между вектором равнодействующей и осями координат x и y определим через направляющие косинусы углов между соответствующей осью и равнодействующей:

Зная направляющие косинусы, через арккосинус есть возможность найти сами углы.

Условия равновесия тела под действием плоской системы сходящихся сил в аналитической форме

Плоскую систему сходящихся сил можно заменить одной силой, которая носит название равнодействующей.

Для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы равнодействующая была равна нулю. А если равнодействующая равна нулю, то и ее проекции на оси x и y тоже должны равняться нулю. Поскольку проекции
равнодействующей равны алгебраическим суммам проекций составляющих сил, то,
окончательно, иметь условия равновесия тела под действием плоской системы
сходящихся сил

Для равновесия тела, находящегося под действием плоской системы сходящихся
сил, необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на оси
координат были равны нулю.

Услуги по теоретической механике:

Учебные лекции:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Как составить уравнение проекций ?

Автор: Константин Вавилов · Опубликовано 23.09.2016 · Обновлено 28.11.2017

При решении задачек по статике, в теоретической механике или при решении задач по сопромату, часто, требуется определять сумму проекций сил на какую-то ось. Например, в термехе это используется при приведении какой-то системы сил к простейшему виду. В сопромате для определения реакций возникающих в опорах.

Уравнения проекций на примере

Рассмотрим, как составить уравнение проекций всех сил на какую-либо ось на примере. Возьмем прямоугольную декартову систему координат x-y и произвольную систему сил:

Проецируем все силы на координатные оси.Сила F1 дает положительную проекцию на ось X, так как ее направление совпадает с направлением этой оси. На ось Y эта сила не дает проекции, так как она перпендикулярная этой оси. Рассуждая, таким образом, можно записать следующие уравнения сумм проекций:

В выше описанном примере все силы были параллельны или перпендикулярны осям, но на практике же в задачах обычно силы расположены под некоторым углом к координатным осям. В таком случае силы раскладываются на две проекции параллельные осевым линиям:

Для нахождения этих сил удобнее вынести отдельно силовой треугольник и найти их следующим образом:

После этого можно записать уравнение проекций сил на горизонтальную и вертикальную ось: