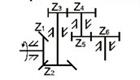
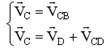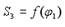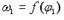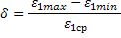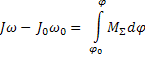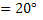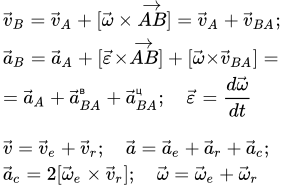Система векторных уравнений для определения скорости

Виброактивность и защита машин. Кинематическая пара, имеющая следующее условное обозначение, называется

Структурный анализ

Кинематическая пара, имеющая следующее условное обозначение, называется

Сферической с пальцем

Структурный анализ

Кинематическая пара, имеющая следующее условное обозначение, называется

Сферической с пальцем

Структурный анализ

На рисунке приведено условное обозначение (по ГОСТ 2.770-68*)…

*Вращательной кинематической пары

Поступательной кинематической пары

Цилиндрической кинематической пары

Сферической кинематической пары

Винтовой кинематической пары

Структурный анализ

Порядок структурной группы определяется…

Числом кинематических пар, входящих в структурную группу

*Числом элементов кинематических пар для присоединения других звеньев

Числом сторон замкнутого контура

Числом звеньев, входящих в структурную группу

Числом кинематических пар, образующих замкнутый контур

Структурный анализ

Звено, которому сообщается движение, преобразуемое механизмом в движение других звеньев, называется…

Структурный анализ

Звено рычажного механизма, вращающееся вокруг неподвижной оси и образующее с другим подвижным звеном поступательную пару, называется…

Структурный анализ

Токарно-винторезный станок является машиной…

Структурный анализ

Условие статической определимости плоской кинематической цепи имеет вид…(n-число звеньев кинематической цепи; Рн — число низших кинематических пар; Рв — число высших кинематических пар)…

Структурный анализ

Порядок структурной группы равен…

Структурный анализ

Число связей у цилиндрической кинематической пары равно.

Структурный анализ

Структурной группой звеньев (группой Ассура) называется…

Незамкнутая кинематическая цепь

Кинематическая цепь, которая может образовывать замкнутый контур

Кинематическая цепь, которая в случае присоединения её элементами кинематических пар к стойке, имеет подвижность равную единице

*Кинематическая цепь, которая в случае присоединения её элементами кинематических пар к стойке, имеет нулевую подвижность

Система звеньев образующих между собой только вращательные кинематические пары

Структурный анализ

Число степеней свободы винтовой кинематической пары равно…

Структурный анализ

Механизм, в котором преобразовании движения происходит посредством твердых и жидких тел, называется…

Структурный анализ

Храповый механизм является…

* Механизмом с остановками выходного звена

Структурный анализ

Числом степеней свободы механизма с голономными связями называется…

Наибольшее число кинематических пар, входящих в замкнутый контур

*Число обобщенных координат механизма

Число подвижных звеньев механизма

Число кинематических пар механизма

Число выходных звеньев механизма

Структурный анализ

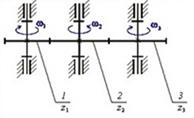
Число вращательных кинематических пар в механизме, структурная схема которого приведена на рисунке, равно…

Структурный анализ

Число поступательных кинематических пар в механизме, структурная схема которого приведена на рисунке равно…

Структурный анализ

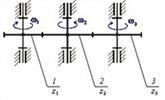
Число поступательных кинематических пар в механизме, структурная схема которого приведена на рисунке, равно…

Структурный анализ

Кинематическая цепь, структурная схема которой приведена на рисунке, является…

Плоской простой незамкнутой

Плоской сложной незамкнутой

Пространственной простой замкнутой

*Пространственной простой незамкнутой

Плоской сложной замкнутой

Структурный анализ

Пневматическим механизмом называется механизм, в котором преобразование движения происходит посредством…

Только жидких тел

Только твердых тел

Твердых и жидких тел

*Твердых и газообразных тел

Структурный анализ

Если число связей кинематической пары равно 1,то число степеней свободы равно…

Структурный анализ

Число степеней свободы W манипулятора равно…

Структурный анализ

Условно статической определимости удовлетворяет…

Любая кинематическая цепь с числом звеньев не более трех

Любая кинематическая цепь

*Любая группа Ассура

Любая кинематическая цепь, содержащая только низшие кинематические пары

Структурный анализ

Структурная группа показанная на рисунке, относится ко (к)____классу…

Структурный анализ

Механизм, структурная схема которого показана на рисунке, относится к…

Структурный анализ

Число степеней свободы пространственного механизма, структурная схема которого приведена на рисунке, равно…

Кинематический анализ

Отношение действительного значения физической величины, к длине отрезка, которым эта величина изображается на чертеже называется…

Аналогом скорости точки

Кинематический анализ

Точка D кулисы будет занимать крайние положения, если точка D кривошипа будет расположена в точках…

Кинематический анализ

Верным планом ускорения для данного положения механизма (n₁=const) является…

Кинематический анализ

Кинематическим анализом механизма называется…

Определение движения звеньев механизма по приложенным к ним силам или определение сил по заданному движению звеньев

Определение реакций, действующих в кинематических парах механизма

Определение уравновешивающей силы на входном звене механизма

* Определение движения звеньев механизма по заданному движению начальных звеньев

Определение количества кинематических пар из которых составлен механизм

Кинематический анализ

Точка С ползуна будет занимать крайние положения, если точка В кривошипа будет расположена в точках…

Кинематический анализ

Верным планом ускорений для данного положения механизма (n₁=const), является…

Кинематический анализ

Верной системой векторных уравнений для определения скорости точки С шарнирного четырехзвенника является…

Кинематический анализ

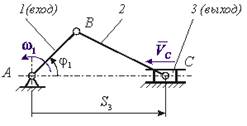
На рисунке приведена кинематическая схема кривошипно-ползунного механизма компрессора. Функция положения этого механизма записывается в виде…

Кинематический анализ

Звено 2 в механизме называется…

Кинематический анализ

Угол размаха кулисы обозначен цифрой…

Кинематический анализ

Верным планом скоростей для данного положения механизма является…

Кинематический анализ

Ход ползуна 3 Н кривошипно-ползунного механизма (см. рисунок) определяется зависимостью…

(L_ав – длина кривошипа 1; L_вс – длина шатуна 3)

Кинематический анализ

Механизм, структурная схема которого показана на рисунке, называется…

Шарнирным четырехзвенным механизмом

Кинематический анализ

Аналогом угловой скорости называется…

Первая производная угла по времени

Вторая производная угла поворота по времени

Производная ускорения точки по времени

Вторая производная угла поворота по обобщенной координате механизма

* Первая производная угла поворота звена по обобщенной координате механизма

Кинетостатический анализ

Силовой расчет механизмов методами кинетостатики основан на применении…

Принципа возможных перемещений

Уравнения Лагранжа второго рода

Теоремы об изменении кинетической энергии

Кинетостатический анализ

Главный вектор сил инерции звена, совершающего поступательное движение, направлен…

В ту же сторону, что и ускорение звена

* Противоположно направлению ускорения звена

В ту же сторону, что и скорость звена

Противоположно направлению скорости звена

Кинетостатический анализ

Уравнения, устанавливающие взаимосвязь между кинематическими характеристиками движения механизма, приложенными к ним силами, размерами, массами и моментами инерции звеньев называются…

Уравнениями движения механизма

Уравнениями замкнутого векторного контура

Уравнениями преобразования координат

Динамика механизмов

Условие существования режима разгона записывается как ( = )…

* d

Динамика механизмов

Условие существования режима торможения записывается как ( = )…

* d

Динамика механизмов

Условие существования установившегося движения записывается как ( = )…

* d

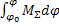
Динамика механизмов

Установившимся движением механизма называется …

*Движение, при котором кинетическая энергия механизма постоянна или является периодической функцией времени

Движение, при котором кинетическая энергия механизма возрастает

Движение, при котором кинетическая энергия механизма убывает

Движение, при котором направление угловой скорости начального звена механизма не меняется

Динамика механизмов

Режимом выбега механизма называется…

Движение, при котором кинетическая энергия механизма постоянна или является периодической функцией времени

Переходное движение между покоем и установившимся движением механизма

*Переходное движение между установившимся движением механизма и покоем

Движение, при котором направление угловой скорости начального звена механизма не меняется

Динамика механизмов

Режимом разбега механизма называется…

*Переходное движение между покоем и установившимся движением механизма

Переходное движение между установившимся движением механизма и покоем

Движение, при котором направление угловой скорости начального звена механизма не меняется

Динамика механизмов

На рисунке приведен график зависимости угловой скорости начального звена механизма от времени t. Режим движения механизма, соответствующий участку 2 графика, называется …

Фазой неустановившегося движения

*Фазой установившегося движения

Динамика механизмов

Главный вектор сил инерции и главный момент сил инерции точек звена, совершающего равномерное прямолинейное поступательное движение, удовлетворяют соотношениям…

Динамика механизмов

Главный вектор сил инерции и главный момент сил инерции точек звена, совершающего равномерное вращательное движение вокруг оси, проходящей через центр масс, удовлетворяют соотношениям…

Динамика механизмов

Необходимое условие режима разбега механизма записывается в виде … ( А_дв— работа движущих сил за цикл движения механизма; А_с— работа сил сопротивления за цикл движения механизма)

Динамика механизмов

На рисунке приведена структурная схема кривошипно-ползунного механизма компрессора. Коэффициент неравномерности движения этого механизма определяется по форме …

( угловой скорости начального звена за цикл движения механизма; — максимальное, минимальное и среднее значение углового ускорения начального звена механизма за цикл движения механизма; — максимальное, минимальное и среднее значение скорости выходного звена за цикл движения механизма; — максимальное, минимальное и среднее значение ускорения выходного звена за цикл движения механизма)

Динамика механизмов

Статическим уравновешиванием вращающегося звена называется…

Распределение масс вращающего звена, при котором главные центральные оси инерции не пересекают ось вращения звена

Распределение масс вращающего звена, при котором одна из его главных центральных осей инерции располагается параллельно оси вращения

Распределение масс вращающего звена, совмещающее одну из его главных центральных осей инерции с осью вращения

*Распределение масс вращающего звена, переводящее его центр масс на ось вращения

Динамика механизмов

Уравнение движения механизма с одной степенью свободы в энергетической форме записывается как ( – начальные значения соответствующих переменных)…

* =

Динамика механизмов

кривошипно-ползунный механизм имеет три подвижных звена, центры масс которых обозначены . Укажите схему расположения противовесов, которая позволяет осуществлять полное статическое уравновешивание масс механизма.

Динамика механизмов

Динамика механизмов изучает …

Деформации звеньев механизмов, возникающие при их движении

*Движение звеньев механизмов под действием некоторой системы сил

Движение механизмов с геометрической точки зрения, без учета действующих сил

Методы расчета звеньев механизмов на прочность и жесткость

Динамика механизмов

Целью динамического анализа механизма является …

*Определение движения звеньев механизма по приложенным к ним силам или определение сил по заданному движению при известных размерах, массах и моментах инерции звеньев

Установление взаимосвязей между скоростями движения входного и выходного звеньев механизма

Определение числа степеней свободы механизма по заданной структурной схеме

Определение масс, моментов инерции и размеров его звеньев, обеспечивающих заданные кинематические характеристики движения

Определение размеров звеньев механизма, обеспечивающих заданный ход выходного звена

Динамика механизмов

Коэффициентом неравномерности движения механизма называется …

*Отношение разности максимального и минимального значений скорости начального звена механизма к её среднему значению за один цикл установившегося движения механизма

Отношение средних скоростей выходного звена на рабочем и холостом ходах

Разность максимального и минимального значений скорости начального звена механизма

Отношение разности максимального и минимального значений скорости выходного звена механизма к её среднему значению за один цикл установившегося движения механизма

Динамика механизмов

Главный вектор сил инерции и главный момент сил инерции точек звена, совершающего ускоренное вращательное движение вокруг оси, не проходящей через центр масс, удовлетворяют соотношениям…

Динамика механизмов

Главный вектор сил инерции и главный момент сил инерции точек звена, совершающего ускоренное поступательное движение, удовлетворяют соотношениям…

Теория зубчатых зацеплений

Для зацепления, по действующему в России законодательству, профильный угол эвольвенты 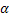для точки лежащей на делительной окружности, равен …

α = 0

α = 24

*α

α = 26

= 30

Теория зубчатых зацеплений

Для нарезания колес с внутренними зубьями используется зуборезный инструмент — …

Гребенка и червячная фреза

Теория зубчатых зацеплений

Укажите схему планетарного зубчатого механизма

Теория зубчатых зацеплений

Паразитными колесами в данном редукторе являются …

Теория зубчатых зацеплений

Передаточное число данного редуктора вычисляется по формуле …

Теория зубчатых зацеплений

Передаточное число данного редуктора вычисляется по формуле …

Теория зубчатых зацеплений

Если то передаточное отношение редуктора равно …

Теория зубчатых зацеплений

Условие соосности в планетарной передаче, структурная схема которой приведена на рисунке, выражается соотношением

Теория зубчатых зацеплений

Передаточное отношение многоступенчатой зубчатой передачи (см. рисунок) рассчитывается по формуле …

Теория зубчатых зацеплений

На рисунке приведена структурная схема многоступенчатой зубчатой передачи. Если число зубьев зубчатого колеса 3 , увеличить в два раза, то угловая скорость этого колеса

Увеличится в два раза

*Уменьшится в два раза

Увеличится в четыре раза

Теория зубчатых зацеплений

На рисунке приведена структурная схема многоступенчатой зубчатой передачи. Если число зубьев зубчатого колеса 2 , увеличить в два раза, то передаточное отношение

Увеличится в два раза

Уменьшится в два раза

Увеличится в четыре раза

Теория зубчатых зацеплений

На рисунке приведена структурная схема многоступенчатой зубчатой передачи. Для увеличения угловой скорости зубчатого колеса 3 , можно …

Увеличить число зубьев зубчатого колеса 2

Уменьшить число зубьев зубчатого колеса 1

Уменьшить число зубьев зубчатого колеса 2

*Уменьшить число зубьев зубчатого колеса 3

Теория зубчатых зацеплений

Модуль прямозубого цилиндрического эвольвентного зубчатого колеса определяется зависимостью … ( — делительный окружной шаг зубьев; — окружная толщина зуба по делительной окружности; = окружная ширина впадины по делительной окружности)

*m =

m =

Теория зубчатых зацеплений

Согласно действующему в России государственному стандарту диаметр начальной окружности прямозубого цилиндрического эвольвентного зубчатого колеса обозначается …

Теория зубчатых зацеплений

Для эвольвентного зацепления характерно свойство …

В процессе зацепления не происходит относительное скольжение зубьев, а также удельное давление зубьев не меняется

Эвольвентное зацепление не обеспечивает постоянство передаточного отношения в процессе зацепления

В процессе зацепления удельное давление одного зуба на другой не меняется

В процессе зацепления не происходит скольжения зубьев относительно друг друга

*Эвольвентное зацепление обеспечивает постоянство передаточного отношения в процессе зацепления

Теория зубчатых зацеплений

Диаметр основной окружности определяется по формуле …

* = d cos( )

= d sin( )

= d + cos( )

= d / cos( )

= d tg( )

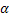
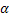
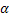
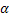
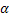
Теория зубчатых зацеплений

Для эвольвентного зацепления характерно свойство …

*Эвольвентное зацепление обеспечивает постоянство передаточного отношения в процессе зацепления

Эвольвентное зацепление не обеспечивает постоянство передаточного отношения в процессе зацепления

В процессе зацепления удельное давление одного зуба на другой не меняется

В процессе зацепления не происходит скольжение зубьев относительно друг друга

Теория зубчатых зацеплений

Коэффициент удельного давления в зубчатой передаче характеризуется …

Величину проскальзывания сопряженных профилей зубчатых колес в процессе зацепления

*Величину контактных напряжений, возникающих в местах соприкосновения зубьев

Непрерывность и плавность зацепления в передаче

Изменение межосевого расстояния зубчатой передачи при нарезании входящих в нее зубчатых колес со смещением

Изменение передаточного отношения зубчатой передачи вследствие неточности изготовления зубчатых колес

Кулачковые механизмы

Фазовый угол изображенный на рисунке, называется …

Углом ближнего стояния (нижней паузы)

Углом дальнего стояния (верхней паузы)

Углом сближения (приближения)

Кулачковые механизмы

Если — угол удаления; — угол дальнего стояния; — угол сближения; — угол ближнего стояния, то рабочий профильный угол определяется формулой …

Кулачковые механизмы

Звено 2 механизма, структурная схема которого приведена на рисунке, называется …

Кулачковые механизмы

На рисунке приведены графики зависимости аналогов скорости и ускорения толкателя в кулачковом механизме от угла поворота кулачка на фазе удаления. Данный закон движения толкателя называется …

Кулачковые механизмы

На рисунках ответов приведены графики зависимости аналогов ускорения и скорости от угла поворота кулачка. Укажите закон движения толкателя, при котором возникают «жесткие» удары.

Кулачковые механизмы

Угол давления в кулачковом механизме обозначен цифрой…

3 2 4 1 ниодин из изображенных

Кулачковые механизмы

На рисунках ответов приведены графики зависимости аналогов ускорения и скорости толкателя от угла поворота кулачка. Укажите закон движения толкателя, при котором возникают «мягкие» удары.

Трение

Трение верчения называется…

Внешнее трение при относительном качении соприкасающихся тел

*Внешнее трение при относительном вращении одного тела относительно другого вокруг общей нормали к поверхностям соприкосновения

Внешнее трение при относительном покое соприкасающихся тел

Внешнее трение при относительном скольжении соприкасающихся тел

Трение

Трение скольжения называется…

*Внешнее трение при относительном скольжении соприкасающихся тел

Внешнее трение при относительном вращении одного тела относительно другого общей нормали к поверхностям их соприкосновения

Внешнее трение при относительном покое соприкасающихся тел

Внешнее трение при относительном качении соприкасающихся тел

Трение

Внутренним трением называется…

Противодействие относительному перемещению соприкасающихся тел

Противодействие относительному перемещению соприкасающихся тел в направлении, нормальном к плоскости их соприкосновения

*Противодействие относительному перемещению отдельных частей одного и того же тела при его деформации

Противодействие относительному перемещению соприкасающихся тел в направлении, лежащем в плоскости их соприкосновения

Трение

Трение покоя называется…

Внешнее трение при относительном движении соприкасающихся тел

*Внешнее трение при относительном покое соприкасающихся тел

Внутреннее трение в стойке механизма

Внутреннее трение при малых деформациях твердых тел

Трение

Жидкостным (гидродинамическим) трением называется…

Внешнее трение, при котором трущиеся поверхности соприкасающихся тел покрыты пленками окислов и адсорбированными молекулами газов или жидкостей, а смазка отсутствует

*Трение, при котором поверхности трущихся твердых тел полностью отделены друг от друга слоем жидкости

Внешнее трение, при котором между трущимися поверхностями соприкасающихся тел есть тонкий (порядка 0,1 мкм и менее) слой смазки, обладающий свойствами, отличными от её обычных объемных свойств

Внешнее трение, при котором между трущимися поверхностями соприкасающихся тел есть слой смазки с обычными объемными свойствами

Трение

Ползун 1 движется по направляющей 2 со скоростью V под действием внешних сил , . Углом трения является угол

b d a g

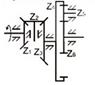
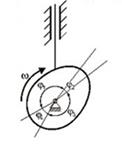
Виброактивность и защита машин

Виброгаситель, изображенный на рисунке, называется…

Кинематика. Все определения, понятия, законы и теоремы

Определение кинематики

Кинематика точки

Способы задания движения точки

Существуют следующие способы задания движения точки:
1) векторный; 2) координатный; 3) естественный.

Векторный способ задания движения точки

При векторном способе задания движения точки, положение точки определяется ее радиус-вектором , проведенным из некоторого центра O . При этом, радиус-вектор является функцией от времени t .

Радиус-вектор – это вектор, проведенный от предварительно выбранного центра O к материальной точке M :
.
Годограф вектора – это линия, которую вычерчивает конец вектора при его изменении во времени. При этом начало вектора находится в определенной точке пространства и его положение не меняется со временем.

Таким образом, траектория точки является годографом ее радиус-вектора.

Координатный способ задания движения точки

При координатном способе задания движения точки, мы выбираем систему координат. Обычно это прямоугольная система, но можно выбрать любую другую: цилиндрическую, сферическую и т. п. Тогда положение точки в пространстве определяется тремя координатами. В прямоугольной системе, их обозначают, как правило, буквами x, y, z. Зависимости этих координат от времени определяют закон движения точки:
.

Если движение происходит в одной плоскости, то мы выбираем систему координат в этой плоскости. В результате получаем два уравнения движения:
.
Исключив из этих уравнений параметр t , можно определить траекторию движения в виде функции , или .

При прямолинейном движении, выбрав ось x системы координат вдоль линии движения, имеем одну зависимость . Эта зависимость называется законом прямолинейного движения точки.

Связь между координатным и векторным способами задания движения точки

Пусть x, y, z – координаты точки в прямоугольной системе координат. Тогда
,
где – единичные векторы, проведенные в направлениях координатных осей;
– модуль вектора ;
– направляющие косинусы вектора . То есть это косинусы углов между вектором и осями координат.

Естественный способ задания движения точки

При естественном способе, система координат связана с траекторией движения точки. При этом мы считаем, что сама траектория нам известна. На этой траектории, мы выбираем положение неподвижного центра O . Тогда положение точки определяется длиной дуги s кривой, измеренной вдоль траектории от центра O до положения точки в момент времени t . Закон движения точки определяется как зависимость .

Дуговая координата s – это длина дуги траектории от некоторого неподвижного центра O до текущего положения точки. При этом в качестве центра O выбирается любая точка, принадлежащая траектории. Она является началом отсчета длины дуги s .

Переход от координатного способа к естественному выполняется по формулам:
;
.

Скорость точки

В прямоугольной системе координат, вектор скорости можно записать так:
.
Проекции скорости на оси координат (компоненты) равны производным координат по времени:
.
Модуль скорости: .
Направляющие косинусы: – это косинусы углов между вектором скорости и осями координат.

Равномерное движение точки – это движение, при котором модуль скорости остается постоянным.

Скорость при естественном способе задания движения

Вектор скорости направлен по касательной к траектории:
,
где – единичный вектор, направленный по касательной к траектории в сторону увеличения длины дуги s .
Абсолютная величина скорости равна абсолютной величине производной длины дуги траектории по времени:
.
Если , то движение происходит в сторону увеличения дуговой координаты s . Если , то дуговая координата уменьшается.

Удобно ввести алгебраическую величину скорости . Она равна проекции скорости на направление единичного вектора :
.
Это скалярная величина. В отличии от модуля скорости, она может иметь как положительное, так и отрицательное значение. Далее мы будем использовать следующие обозначения:
– это вектор скорости;
– его абсолютная величина;
– алгебраическая величина скорости – проекция скорости на направление вектора . При движение происходит в сторону увеличения дуговой координаты. При – в сторону уменьшения. Тогда
; .

Ускорение точки

Проекции ускорения на оси координат:
.
Модуль ускорения: .
Направляющие косинусы: .

Ускорение при естественном способе задания движения

При естественном способе задания движения, ускорение раскладывают на два взаимно перпендикулярных вектора: касательное (тангенциальное) к траектории, и нормальное (перпендикулярное) ускорение:
.
Модуль ускорения .

Касательное ускорение:
.
Здесь, как и для скорости, мы считаем, что – это скалярная величина, которая может принимать как положительные, так и отрицательные значения. Тогда
.
Продифференцировав модуль скорости по времени, получим:
.
Отсюда следует, что абсолютное значение производной модуля скорости по времени равно модулю касательного ускорения. Если угол между направлениями векторов ускорения и скорости острый, , то происходит увеличение скорости – ускоренное движение. Если угол тупой , то происходит уменьшение скорости – замедленное движение.

Нормальное ускорение перпендикулярно касательной к траектории и всегда направлено к центру кривизны:
.
Здесь – единичный вектор в направлении главной нормали траектории.
Пусть ρ – радиус кривизны траектории. Тогда модуль нормального ускорения
.

Вектор полного ускорения точки лежит в соприкасающейся плоскости к траектории. Поэтому его проекция на бинормаль равна нулю:
.

Скорость и ускорение точки в полярной системе координат

В полярной системе координат , положение точки M определяется по формулам:
.
Пусть – единичные векторы (орты), проведенные из точки M в сторону увеличения r и φ , соответственно. Тогда вектор скорости выражается через них по формуле:
.
Модуль скорости: ,
где – радиальная скорость; – поперечная скорость.

Ускорение точки
.
Радиальное ускорение: . Поперечное ускорение: . Модуль ускорения: .

Классификация движений точки

1) Прямолинейное равномерное движение.
. В этом случае скорость точки постоянна. Движение происходит по прямой, параллельной вектору скорости.

2) Криволинейное равномерное движение.
. Скорость точки постоянна по абсолютной величине, но движение происходит не по прямой, а по кривой.

3) Прямолинейное неравномерное движение.
. Скорость точки изменяется по абсолютной величине, но траектория прямолинейна.

4) Криволинейное неравномерное движение.
. Скорость точки меняется как по абсолютной величине, так и по направлению. Если направления векторов и совпадают, то это ускоренное движение. В противном случае – замедленное.

5) Равнопеременное криволинейное движение.
. Это частный случай криволинейного неравномерного движения. Здесь касательное ускорение постоянно. Алгебраическая величина скорости меняется по линейному закону: . Длина дуги траектории – по квадратичному: .

Кинематика твердого тела

Общие теоремы

Расстояния между любыми двумя точками абсолютно твердого тела не меняется в процессе его движения. Эти связи приводят к дополнительным ограничениям на скорости движения точек. В результате получаются уравнения, связывающие скорости и ускорения точек. Такие уравнения носят название формул Эйлера.

Формулы Эйлера
Скорости и ускорения двух точек A и B твердого тела с радиус-векторами и связаны соотношениями:
(Т1) ;
(Т2) .
Здесь – некоторый аксиальный вектор, который называется угловой скоростью;
– вектор углового ускорения.
Доказательство.

Это фундаментальные уравнения. Точку A , при такой форме записи, называют полюсом. Тогда движение твердого тела можно рассматривать как поступательное движение полюса и вращательное движение относительно него.

Отметим еще одну теорему, которую часто применяют в расчетах.

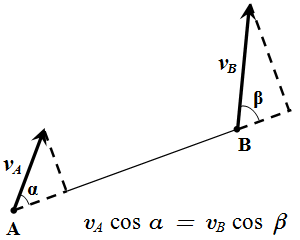
Теорема о проекциях скоростей двух точек твердого тела на прямую
Проекции скоростей двух точек твердого тела на ось, проходящую через эти точки, равны друг другу:
.
Доказательство.

Далее приводится классификация видов движения тела и применение формул Эйлера в конкретных случаях.

Поступательное движение

При поступательном движении все точки тела имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения, их траектории конгруэнтны, а разность радиус-векторов любых двух точек равна вектору, который зависит от положений сравниваемых точек, но не зависит от времени.

При поступательном движении угловая скорость и угловое ускорение равны нулю:
. Тогда формулы Эйлера ⇑ принимают вид:
.

Вращательное движение вокруг неподвижной оси

Определение

При вращении все точки тела движутся в плоскостях, перпендикулярных оси вращения. Их траекториями являются окружности с центром на оси вращения. Положение тела определяется углом поворота φ относительно произвольным образом выбранного нулевого положения. Зависимость угла поворота от времени определяет закон вращательного движения или, что тоже самое, уравнение вращательного движения. Единицей измерения угла поворота является радиан, который считается безразмерной величиной.
180° = π радиан ⇒ 1 радиан = 180/π = 57,29578°.

Угловая скорость и ускорение

Вектор угловой скорости параллелен оси вращения. Его направление определяется правилом правого винта. Он не имеет точки приложения и применим ко всем точкам твердого тела, то есть ко всему телу в целом. Однако, для наглядности, вектор угловой скорости изображают на оси вращения.

Единицей измерения угловой скорости является 1 рад/с или, что тоже самое, 1/с = с –1 . В технике встречаются другие единицы измерения. Пусть n – число оборотов в минуту. Тогда 1 оборот = 2π радиан ; 1 минута = 60 с ; ;
n об/мин = n·2π/60 рад/с. Тогда
.

Угловое ускорение – это производная угловой скорости по времени:
.
Единицей измерения углового ускорения является рад/с 2 или, что тоже самое, с –2 .

Вектор углового ускорения также параллелен оси вращения. При ускоренном вращении он совпадает с направлением угловой скорости. При замедленном – имеет противоположное направление.

Частные случаи вращения тела

Равномерное вращение. Угловая скорость постоянна; угловое ускорение равно нулю: .
Равнопеременное вращение. Угловая скорость линейно меняется со временем; угловое ускорение постоянно: .

Скорости и ускорения точек вращающегося тела

Скорости точек любого твердого тела связаны формулой Эйлера ⇑. Для тела, вращающегося вокруг неподвижной оси, в качестве полюса удобно выбрать любую точку на оси вращения. Тогда скорость точки с радиус-вектором тела, вращающегося с угловой скоростью , определяются по формуле:
.
Здесь – радиус-вектор произвольной точки на оси вращения. Если ось вращения проходит через начало координат, то в качестве можно выбрать точку начала координат . Тогда
.
По правилам векторного произведения,
.
Здесь |CM| – расстояние от точки M до оси вращения (см. рисунок ⇓). Точка M движется по окружности радиуса |CM|. Вектор скорости направлен по касательной к этой окружности в сторону, которая задается направлением вектора угловой скорости.

При вычислении векторного произведения, полезно использовать следующие формулы:

.
Здесь – проекции угловой скорости на оси координат. Таким образом, проекции вектора скорости точки определяются так:
.
Если ось вращения совпадает с осью z, то , .

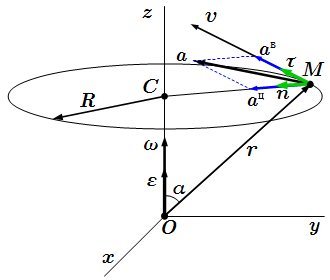
Скорость и ускорение точек твердого тела при вращении вокруг неподвижной оси Oz .

Ускорение точки определяется по формуле:
.

Вращательное ускорение:
;
.
Оно направлено по касательной к траектории и связано с изменением скорости точки по абсолютной величине.

Центростремительное (осестремительное) ускорение:

.
Оно направлено по главной нормали – к центру окружности и по абсолютной величине равно
,
где R – расстояние до оси вращения.

Модуль полного ускорения:
.
Угол β между векторами полного и центростремительного ускорений:
.

Плоское движение твердого тела

При плоском движении, все кинематические величины (перемещения, скорости и т.д.) имеют одинаковые значения для всех плоскостей, параллельных плоскости движения. Поэтому для описания плоского движения, нам достаточно рассмотреть движение любого сечения тела, или как говорят, плоской фигуры. Все результаты, полученные для одной плоской фигуры применимы и для других сечений, параллельных плоскости движения. Хотя плоская фигура имеет свои контуры и характерные точки, но мы считаем, что она не ограничена в размерах, поскольку ее размер может зависеть от выбора сечения. Кроме этого имеются некоторые точки, например мгновенный центр скоростей, которые служат только для проведения расчетов и могут находиться за пределами тела.

Для описания плоского движения, мы выбираем плоскую фигуру; проводим в ней двумерную систему координат x, y. Далее, произвольным образом выбираем точку A . Эту точку мы будем называть полюсом. Тогда положение тела однозначно определяется координатами точки A и углом поворота φ , относительно, произвольным образом выбранного направления, например оси x . При этом движение тела определяется тремя уравнениями, которые называют уравнениями плоского (или плоскопараллельного) движения тела:
.

Эти уравнения также называют уравнениями движения плоской фигуры. При таком описании, движение тела слагается из поступательного движения полюса A , и вращательного движения вокруг него. Поступательное движение зависит от выбора полюса, а угол поворота φ – нет.

Определение скоростей

Скорость точки B с радиус-вектором определяется по формуле Эйлера ⇑:
(П1) .
То есть скорость точки B тела равна векторной сумме скорости полюса A и относительной скорости . Относительное движение является вращением с угловой скоростью относительно оси, проходящей через полюс A перпендикулярно плоскости фигуры. Поскольку вектор угловой скорости перпендикулярен плоскости движения, то он перпендикулярен и вектору скорости. Тогда модуль относительной скорости равен произведению угловой скорости на расстояние от точки до полюса:
.

Мгновенный центр скоростей

Определения и свойства

Далее мы будем обозначать мгновенный центр скоростей буквой P . Для плоской фигуры – это точка. Для твердого тела – это ось, проходящая через точку P перпендикулярно плоскости движения. Эта ось может находиться за пределами тела.

Если плоская фигура движется непоступательно, то мгновенный центр скоростей всегда существует. Для поступательного движения, МЦС находится на бесконечности.

Приняв МЦС P в качестве полюса, получим значение вектора скорости произвольной точки B :
.
Поскольку движение плоское, то . Тогда модуль скорости точки B плоской фигуры равен произведению угловой скорости на расстояние до мгновенного центра скоростей:
.
Вектор скорости перпендикулярен отрезку, соединяющим точку с МЦС и направлен в сторону вращения плоской фигуры.

Скорости точек плоской фигуры пропорциональны их расстояниям до МЦС:
(Ц1) .

Модуль угловой скорости плоской фигуры равен отношению модуля скорости произвольной точки к ее расстоянию до мгновенного центра скоростей:
.

Теорема Шаля
Плоскую фигуру можно переместить из одного положения в любое другое положение одним поворотом этой фигуры вокруг некоторого неподвижного центра, который называют центром вращений, или осью вращений.

Мгновенный центр вращений – это центр вращений, определяемый согласно теореме Шаля, при бесконечно малом перемещении фигуры.

Если рассматривать перемещение плоской фигуры со временем, то мгновенный центр вращений совпадает с мгновенным центром скоростей.

Неподвижная центроида – это геометрическое место мгновенных центров скоростей, отмеченных на неподвижной плоскости.
Подвижная центроида – это геометрическое место мгновенных центров скоростей, отмеченных на плоской фигуре.

Например, если колесо катится без проскальзывания по неподвижной прямой, то неподвижной центроидой является прямая, а подвижной – обод колеса.

Теорема Пуансо
При движении плоской фигуры, подвижная центроида катится без скольжения по неподвижной центроиде.

Определение положения МЦС

1) Если скорости и точек A и B не параллельны, то МЦС есть точка пересечения прямых, проведенных через эти точки, перпендикулярно векторам их скоростей.
2) Если векторы и не равны, параллельны и перпендикулярны прямой AB , то для определения МЦС необходимо знать модули и направления скоростей, и применить формулу (Ц1).
3) Если векторы и равны, то МЦС находится на бесконечности, .
4) Если тело катится без скольжения по неподвижной поверхности, то МЦС находится в точке соприкосновения тела и поверхности.

Определение ускорений

Дифференцируя уравнение Эйлера (П1) по времени, получаем ускорение точки B :
(П1) ;

Итак мы нашли ускорение произвольной точки B плоской фигуры. Этот результат можно представить в следующем виде:
.
То есть ускорение произвольной точки B плоской фигуры равно геометрической сумме ускорения полюса и ускорению этой точки относительно полюса , которое определяется по формулам вращательного движения относительно неподвижного центра A . То есть равно геометрической сумме вращательного и центростремительного ускорений:
.

Вращательное ускорение относительно полюса перпендикулярно отрезку AB , соединяющим точку с полюсом. Центростремительное относительное ускорение направлено от точки B к A . Поскольку угловое ускорение также перпендикулярно AB , то
.

Мгновенный центр ускорений

Чтобы построить точку Q нужно выполнить следующие действия.
1) Из полюса A построить вектор ускорения .
2) Из полюса A провести луч AQ под углом к вектору ускорения полюса так, чтобы направление поворота от к AQ совпадало с направлением углового ускорения ε .
3) На луче AQ построить точку Q на расстоянии от точки A .

Приняв точку Q в качестве полюса, получим ускорение произвольной точки B твердого тела:
,
где – единичный вектор касательной к окружности радиуса QB ; – единичный вектор, направленный от B к Q .

Модули ускорений точек плоской фигуры пропорциональны расстояниям от этих точек до мгновенного центра ускорений:
.
Векторы ускорений составляют с отрезками, соединяющими эти точки и мгновенный центр ускорений один и тот же угол
.
Мгновенный центр скоростей P и мгновенный центр ускорений Q являются различными точками плоской фигуры.

Сферическое движение твердого тела

При сферическом движении, точки тела движутся по сферическим поверхностям. Положение тела часто определяют с помощью трех углов ψ, θ, φ , которые называются углами Эйлера. Для этого вводят две системы координат – неподвижную , и подвижную Oxyz , связанную с телом. Связь между ними осуществляется следующим образом.
1) Поворачиваем неподвижную систему координат на угол ψ вокруг оси . Получаем систему .
2) Поворачиваем систему координат на угол θ вокруг оси ON . Получаем систему ONK′z .
3) Поворачиваем систему координат ONK′z на угол φ вокруг оси Oz . Получаем систему координат Oxyz , связанную с телом.
Ось ON называется линией узлов; ψ – угол прецессии; θ – угол нутации; φ – угол собственного вращения. При движении тела, эти углы являются функциями от времени:
.

Теорема Эйлера – Даламбера
Твердое тело, имеющее одну неподвижную точку, можно переместить из одного положения в любое другое поворотом вокруг некоторой оси, проходящей через неподвижную точку.

Следствие теоремы Эйлера – Даламбера
При сферическом движении твердого тела существует ось, на которой скорости точек равны нулю. Такая ось называется мгновенной осью вращения.

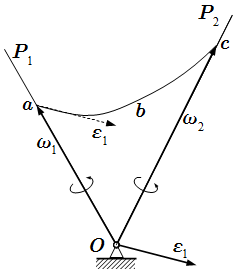
Угловое ускорение ε является касательной к годографу abc угловой скорости. P₁, P₂ – мгновенные оси вращения.

Угловая скорость тела параллельна мгновенной оси вращения. Для удобства ее вектор откладывают из неподвижной точки. При движении, угловая скорость изменяется как по абсолютной величине, так и по направлению. Конец вектора описывает годограф вектора угловой скорости.

Угловое ускорение – это скорость изменения угловой скорости:
.
Оно направлено по касательной к годографу вектора угловой скорости. При сферическом движении, в отличии от случаев вращения вокруг неподвижной оси и плоского движения, направление вектора углового ускорения может не совпадать с направлением вектора угловой скорости.

Скорости точек тела определяются по формуле Эйлера ⇑. В качестве полюса возьмем неподвижную точку O . Тогда для скорости произвольной точки с радиус-вектором имеем: . Если начало координат выбрать в точке O , то , тогда
.
Модуль скорости определяется по формуле:
,
где α – угол между векторами и ; h – расстояние от точки до мгновенной оси вращения.

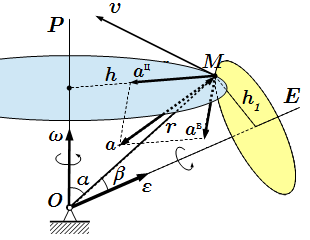
Ускорение при сферическом движении твердого тела.

Ускорение точки определяется по формуле:
.
Вращательное ускорение направлено перпендикулярно плоскости, образованной векторами углового ускорения и радиус-вектором . Оно имеет модуль , где β – угол между векторами и ; – расстояние от точки до оси E, проведенной из неподвижного центра O параллельно вектору углового ускорения.

Центростремительное (осестремительное) ускорение направлено к мгновенной оси вращения P и перпендикулярно ей. По модулю оно равно .

Свободное движение твердого тела

Это самый общий случай движения твердого тела. Свободное тело имеет шесть степеней свободы. Для описания его движения, выберем произвольную точку A тела в качестве полюса. Далее вводим две системы координат – неподвижную OXYZ, и подвижную систему , начало которой в каждый момент времени совпадает с точкой A, а оси параллельны осям неподвижной системы OXYZ. Таким образом, система совершает поступательное движение относительно OXYZ. Тогда свободное движение твердого тела можно рассматривать как сложное движение, состоящее из поступательного движения по закону движения полюса A, и сферического движения в системе координат , с неподвижной точкой A.

Уравнения движения свободного твердого тела представляют собой шесть равенств:
.
Здесь ψ, θ, ϕ – углы Эйлера. Первые три уравнения определяют поступательную часть движения и зависят от выбора полюса. Последние три уравнения определяют сферическое движение, и от выбора полюса не зависят.

Скорость любой точки B тела равна векторной сумме скорости полюса и скорости этой точки при ее сферическом движении относительно полюса:
,
где – радиус-вектор, проведенный из точки A в точку B.

Ускорение точки свободного твердого тела равно векторной сумме ускорения полюса, центростремительного (осестремительного) ускорения точки и ее вращательного ускорения относительно полюса:
.

Сложное движение точки

Для описания сложного движения, мы выбираем неподвижную (основную) систему координат и подвижную . Будем считать, что подвижная система связана с некоторым движущимся твердым телом, относительно которого, в свою очередь движется точка. Например, человек, идущий в движущемся вагоне. Здесь неподвижная система координат – это система, связанная с рельсами и ландшафтом. Твердое тело – вагон. Точка – человек. Подвижная система координат – система, связанная с вагоном. Абсолютное движение – движение человека относительно рельс; относительное движение – движение человека относительно вагона; переносное движение – движение вагона относительно рельс.

Абсолютная скорость (ускорение) точки – это скорость (ускорение) точки в неподвижной системе координат.
Переносная скорость (ускорение) точки – это скорость (ускорение) той точки подвижной системы координат, в которой, в данный момент времени, находится точка, совершающая сложное движение.
Относительная скорость (ускорение) точки – это скорость (ускорение) точки относительно подвижной системы координат.

Теорема о сложении скоростей
При составном движении абсолютная скорость точки равна векторной сумме переносной и относительной скоростей:
.
Модуль абсолютной скорости: .
Эту теорему также называют правилом параллелограмма или треугольника скоростей.

Теорема Кориолиса о сложении ускорений
При составном движении, абсолютное ускорение точки равно векторной сумме переносного , относительного и кориолисова (поворотного) ускорений:
,
где – ускорение Кориолиса (кориолисово ускорение); – угловая скорость вращения подвижной системы координат.

Кориолисово ускорение также называют поворотным ускорением. Оно характеризует изменение направления относительной скорости точки, вызванное вращением подвижной системы координат. Если переносное движение является поступательным, то , кориолисово ускорение равно нулю.

Сложное движение твердого тела

Теперь рассмотрим сложное движение твердого тела – то есть такое движение, при котором твердое тело движется относительно некоторой системы координат , которая, в свою очередь движется относительно неподвижной системы координат . Такое движение часто называют сложением движений. Пусть A – произвольная точка тела, которую мы выберем в качестве полюса. Тогда скорость произвольной точки B тела относительно подвижной системы координат определяется по формуле:
.
В свою очередь, подвижную систему координат также можно рассматривать как твердое тело. Тогда скорость точки B при переносном движении:
.
Применяя теорему о сложении скоростей, найдем скорость точки B относительно неподвижной системы отсчета:
.
Отсюда следует, что скорость полюса относительно неподвижной системы координат равна векторной сумме скоростей полюса при переносном и относительном движениях:
.
Угловая скорость равна векторной сумме угловых скоростей:
.

Рассмотрим частные случаи сложного движения твердого тела.

Сложение двух поступательных движений

При сложении двух поступательных движений, . Тогда . Результирующее движение также является поступательным. Скорость результирующего движения равна сумме скоростей составляющих движений:
.

Сложение вращательных движений вокруг пересекающихся осей

При сложении двух вращательных движений вокруг пересекающихся осей, результирующее движение также является вращательным. При этом ось вращения проходит через точку пересечения осей параллельно вектору абсолютной угловой скорости:
.
Если оси вращения изменяются со временем, то все сказанное выше имеет место для мгновенных осей вращения.

Аналогично предыдущему, при сложении нескольких вращательных движений вокруг пересекающихся осей, результирующее движение также является вращательным. Ось результирующего вращения проходит через точку пересечения осей параллельно вектору абсолютной угловой скорости:
.

Сферическое движение

Как было указано ранее, при сферическом движении, положение тела можно задать с помощью углов Эйлера. Они определяются последовательными переходами от неподвижной системы координат к системе координат , связанной с телом: . Такие переходы можно рассматривать как сложное движение, состоящее из серии вращений ⇑. При этом каждая последующая система координат является повернутой относительно предыдущей на соответствующий угол: ψ, θ, φ , изменяющиеся со временем. Дифференцируя эти углы по времени, получаем угловые скорости вращений систем координат, которые имеют следующие названия:
– угловая скорость прецессии; – угловая скорость нутации; – угловая скорость собственного вращения.

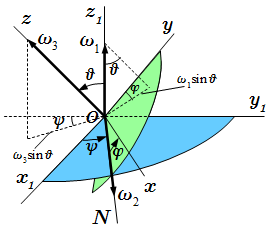
Связь угловых скоростей с углами Эйлера.

Векторы этих угловых скоростей направлены, соответственно, вдоль осей . Тогда вектор угловой скорости тела относительно неподвижной системы координат равен сумме угловых скоростей:
.
Его модуль:
.
Проекции вектора угловой скорости на оси подвижной системы координат Oxyz определяются с помощью кинематических уравнений Эйлера, которые имеют следующий вид:
;
;
.

Сложение вращений вокруг 2-х параллельных осей

Направления вращений совпадают

Если направления вращений совпадают, то угловая скорость, при абсолютном движении, равна сумме модулей угловых скоростей переносного и относительного движений: . Направление вектора совпадает с направлениями векторов и . Движение является плоскопараллельным. Мгновенная ось вращений проходит через точку C (см. рисунок), находящуюся между осями вращений. При этом
;
.

Вращения противоположны

В этом случае, угловая скорость, при абсолютном движении, равна модулю разности абсолютных значений угловых скоростей: , а направление совпадает с направлением наибольшей по абсолютной величине угловой скорости. Движение также является плоскопараллельным. Мгновенная ось вращений проходит через точку C (см. рисунок) так, что ось с наибольшей угловой скоростью оказывается между остальными осями. При этом
;
.

Пара вращений

Пара вращений – это такое сложное движение твердого тела, при котором угловые скорости противоположны по направлению и равны их абсолютные значения: . В этом случае тело совершает поступательное (или мгновенное поступательное движение). Скорости всех точек тела равны . Мгновенная ось вращения находится на бесконечности. Примером такого движения является движение педалей велосипеда относительно рамы.

Сложение поступательного и вращательного движений

Поступательное движение перпендикулярно оси вращения

Если скорость поступательного движения перпендикулярна оси вращения, то это плоскопараллельное движение. Оно имеет мгновенную ось вращения, находящуюся на расстоянии от оси и удаленную от нее в сторону, перпендикулярно вектору .

Винтовое движение

Если скорости и постоянны, то шаг винта также постоянен и определяется по формуле: . При постоянных скоростях и , траекторией любой точки, не лежащей на оси винта, является винтовая линия. При этом скорость точки направлена по касательной к винтовой линии и имеет абсолютное значение , где r – расстояние до оси вращения; – скорость вращательного движения, перпендикулярная оси винта.

Поступательное движение под произвольным углом к оси вращения

Здесь скорость поступательного движения можно разложить на две составляющие – параллельную и перпендикулярную оси вращения . Рассматривая движение в плоскости, перпендикулярной оси вращения, мы можем найти мгновенный центр скоростей P . Он находится на расстоянии от оси . Прибавив сюда скорость , получим винтовое движение с осью . Если скорости меняются со временем, то ось будет мгновенной винтовой осью, а все движение можно рассматривать как состоящее из серии мгновенных винтовых движений вокруг непрерывно изменяющихся винтовых осей. Такое движение называется мгновенно–винтовым движением.

Использованная литература:
А. А. Яблонский, В.М. Никифорова. Курс теоретической механики, часть 1, статика, кинематика. Москва, «Высшая школа», 1966.
С. М. Тарг, Краткий курс теоретической механики, «Высшая школа», 2010.

Автор: Олег Одинцов . Опубликовано: 17-08-2015 Изменено: 29-01-2020

Векторные формулы для скоростей и ускорений точек тела

Представляет скорость, касательную, нормальную и общую скорость тела POINT в формате VECTOR. Точка на модуле относительно направления может быть выражена как векторное произведение (14) Где r — радиус-вектор точки M и задается произвольной заточкой оси вращения Oz, например, точкой O (рис. 35). Уравнение (14) называется векторным уравнением Эйлера. Проверьте, чтобы проверить выражение. Фактически вектор W x G перпендикулярен следующей плоскости. болезнь Рисунок 35.

Поэтому необходимо интегрировать линейные дифференциальные уравнения, соответствующие второму этапу, используя координаты первого этапа и конечное значение скорости в качестве начального условия движения. Людмила Фирмаль

Вектор, содержащийся в векторном произведении. Направление параллельно скорости V вдоль тангенса круга. Модуль векторного производства 2. (16) В справедливости (16) мы убеждены рассчитать их правильную часть. У нас есть ex r | = ersin (s, r) = eh, Это согласуется с тангенциальным ускорением. Направление сектора ххг параллельно вектору тангенциального ускорения (рис. 36). На векторное произведение W x V w x v | = wnsin (w, v) = wi> = hw2 = a „, Это потому, что векторы w и V перпендикулярны друг другу. Направление вектора W x V параллельное N0 векторное регулярное выражение и упорядочение от точки M к оси вращения POET „= — ой w2.

При корректировке вектора h в направлении от оси вращения. Справедливость уравнения (16) установлена. Из определения точечной скорости неизвестно V = dr / dz, Где r — радиус фиксированной точки, особенно точки, нарисованной из любой точки на оси вращения объекта, который вращается вокруг фиксированной оси. Однако скорость точности вращательного движения тела определяется векторной формулой Эйлера (Сравнение двух уравнений для скорости точки дает уравнение для вычисления производной по времени от вектора r. dr / dr = wxr. (17).

Действующая сила определяет только ускорение точки движения, а скорость и положение точки на траектории могут зависеть от скорости и начального положения точки, сообщенной в точке первого мгновения. Людмила Фирмаль

В этом выражении вектор r всегда имеет постоянный модуль, потому что он соединяет две точки сплошного модуля. Вектор

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

источники:

http://1cov-edu.ru/mehanika/kinematika/

http://lfirmal.com/vektornye-formuly-dlya-skorostej-i-uskorenij-tochek-tela/