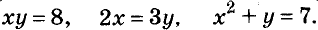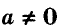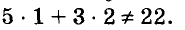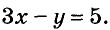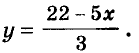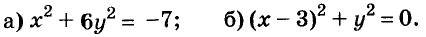Линейная зависимость системы векторов. Коллинеарные векторы
В данной статье мы расскажем:
- что такое коллинеарные векторы;
- какие существуют условия коллинеарности векторов;
- какие существуют свойства коллинеарных векторов;
- что такое линейная зависимость коллинеарных векторов.
Коллинеарные векторы
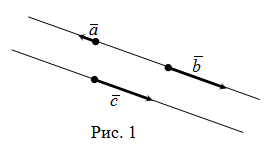
Коллинеарные векторы — это векторы, которые являются параллелями одной прямой или лежат на одной прямой.
Условия коллинеарности векторов
Два векторы являются коллинеарными, если выполняется любое из следующих условий:
- условие 1. Векторы a и b коллинеарны при наличии такого числа λ , что a = λ b ;
- условие 2. Векторы a и b коллинеарны при равном отношении координат:
a = ( a 1 ; a 2 ) , b = ( b 1 ; b 2 ) ⇒ a ∥ b ⇔ a 1 b 1 = a 2 b 2
- условие 3. Векторы a и b коллинеарны при условии равенства векторного произведения и нулевого вектора:
Условие 2 неприменимо, если одна из координат вектора равна нулю.
Условие 3 применимо только к тем векторам, которые заданы в пространстве.
Примеры задач на исследование коллинеарности векторов
Исследуем векторы а = ( 1 ; 3 ) и b = ( 2 ; 1 ) на коллинеарность.
В данном случае необходимо воспользоваться 2-м условием коллинеарности. Для заданных векторов оно выглядит так:
Равенство неверное. Отсюда можно сделать вывод, что векторы a и b неколлинеарны.
Ответ: a | | b
Какое значение m вектора a = ( 1 ; 2 ) и b = ( — 1 ; m ) необходимо для коллинеарности векторов?
Используя второе условие коллинераности, векторы будут коллинеарными, если их координаты будут пропорциональными:
Отсюда видно, что m = — 2 .
Ответ: m = — 2 .
Критерии линейной зависимости и линейной независимости систем векторов
Система векторов векторного пространства линейно зависима только в том случае, когда один из векторов системы можно выразить через остальные векторы данной системы.
Пусть система e 1 , e 2 , . . . , e n является линейно зависимой. Запишем линейную комбинацию этой системы равную нулевому вектору:
a 1 e 1 + a 2 e 2 + . . . + a n e n = 0
в которой хотя бы один из коэффициентов комбинации не равен нулю.
Пусть a k ≠ 0 k ∈ 1 , 2 , . . . , n .
Делим обе части равенства на ненулевой коэффициент:
a k — 1 ( a k — 1 a 1 ) e 1 + ( a k — 1 a k ) e k + . . . + ( a k — 1 a n ) e n = 0
— a k — 1 a m , где m ∈ 1 , 2 , . . . , k — 1 , k + 1 , n
β 1 e 1 + . . . + β k — 1 e k — 1 + β k + 1 e k + 1 + . . . + β n e n = 0
или e k = ( — β 1 ) e 1 + . . . + ( — β k — 1 ) e k — 1 + ( — β k + 1 ) e k + 1 + . . . + ( — β n ) e n
Отсюда следует, что один из векторов системы выражается через все остальные векторы системы. Что и требовалось доказать (ч.т.д.).
Пусть один из векторов можно линейно выразить через все остальные векторы системы:
e k = γ 1 e 1 + . . . + γ k — 1 e k — 1 + γ k + 1 e k + 1 + . . . + γ n e n
Переносим вектор e k в правую часть этого равенства:
0 = γ 1 e 1 + . . . + γ k — 1 e k — 1 — e k + γ k + 1 e k + 1 + . . . + γ n e n
Поскольку коэффициент вектора e k равен — 1 ≠ 0 , у нас получается нетривиальное представление нуля системой векторов e 1 , e 2 , . . . , e n , а это, в свою очередь, означает, что данная система векторов линейно зависима. Что и требовалось доказать (ч.т.д.).
- Система векторов является линейно независимой, когда ни один из ее векторов нельзя выразить через все остальные векторы системы.
- Система векторов, которая содержит нулевой вектор или два равных вектора, линейно зависима.
Свойства линейно зависимых векторов
- Для 2-х и 3-х мерных векторов выполняется условие: два линейно зависимых вектора — коллинеарны. Два коллинеарных вектора — линейно зависимы.
- Для 3-х мерных векторов выполняется условие: три линейно зависимые вектора — компланарны. (3 компланарных вектора — линейно зависимы).
- Для n-мерных векторов выполняется условие: n + 1 вектор всегда линейно зависимы.
Примеры решения задач на линейную зависимость или линейную независимость векторов
Проверим векторы a = 3 , 4 , 5 , b = — 3 , 0 , 5 , c = 4 , 4 , 4 , d = 3 , 4 , 0 на линейную независимость.
Решение. Векторы являются линейно зависимыми, поскольку размерность векторов меньше количества векторов.
Проверим векторы a = 1 , 1 , 1 , b = 1 , 2 , 0 , c = 0 , — 1 , 1 на линейную независимость.
Решение. Находим значения коэффициентов, при которых линейная комбинация будет равняться нулевому вектору:
x 1 a + x 2 b + x 3 c 1 = 0
Записываем векторное уравнение в виде линейного:
x 1 + x 2 = 0 x 1 + 2 x 2 — x 3 = 0 x 1 + x 3 = 0
Решаем эту систему при помощи метода Гаусса:
1 1 0 | 0 1 2 — 1 | 0 1 0 1 | 0
Из 2-ой строки вычитаем 1-ю, из 3-ей — 1-ю:
1 1 0 | 0 1 — 1 2 — 1 — 1 — 0 | 0 — 0 1 — 1 0 — 1 1 — 0 | 0 — 0
1 1 0 | 0 0 1 — 1 | 0 0 — 1 1 | 0
Из 1-й строки вычитаем 2-ю, к 3-ей прибавляем 2-ю:
1 — 0 1 — 1 0 — ( — 1 ) | 0 — 0 0 1 — 1 | 0 0 + 0 — 1 + 1 1 + ( — 1 ) | 0 + 0
0 1 0 | 1 0 1 — 1 | 0 0 0 0 | 0
Из решения следует, что у системы множество решений. Это значит, что существует ненулевая комбинация значения таких чисел x 1 , x 2 , x 3 , при которых линейная комбинация a , b , c равняется нулевому вектору. Следовательно, векторы a , b , c являются линейно зависимыми.
Лекции по высшей математике, линейная алгебра (стр. 4 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 |
Запишем в разных видах систему уравнений 



x 1 


Вектор`x * = 
Система уравнений называется совместной, если она имеет хотя бы одно решение.
Система уравнений называется несовместной, если она не имеет ни одного решения.
Система уравнений называется определенной, если она имеет ровно одно решение.
Система уравнений называется неопределенной, если она имеет более одного решения.
2. СИСТЕМЫ n ЛИНЕЙНЫХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ.
Квадратная матрица A называется невырожденной, если ее строки линейно независимы.
Согласно этому определению, свойствам определителей, критерию существования обратной матрицы получаем, что невырожденная матрица имеет ненулевой определитель и обладает обратной матрицей.
Благодаря этим свойствам имеем два особых метода решения системы A`x =`b с квадратной невырожденной матрицей A.
МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СЛУ.
Если матрица A системы A`x =`b квадратная невырожденная, то существует единственное решение`x * этой системы, равное произведению обратной матрицы A– 1 на столбец свободных членов`b, `x * = A– 1`b.
Докажем сначала, что вектор`x * является решением системы A`x =`b. В самом деле, A`x * = A · A– 1`b = E`b =`b, то есть A`x * =`b и`x * является решением системы A`x =`b.
Докажем теперь единственность этого решения. Предположим, что имеется еще другое решение`x 1, то есть A`x 1 =`b — верное равенство. Домножим обе части этого равенства слева на A– 1. Получим A– 1 A`x 1 = A– 1`b и, следовательно,`x 1 = A– 1`b, то есть`x 1 =`x *. Теорема доказана.
Таким образом, матричный метод решения системы A`x =`b с квадратной невырожденной матрицей A состоит в нахождении решения этой системы по формуле`x * = A– 1`b.
Если матрица A системы A`x =`b квадратная невырожденная, то существует единственное решение`x * = 



ПРИМЕР решения системы линейных уравнений по правилу Крамера.

D = 





3. ОБЩИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ.
Рассмотрим систему уравнений A`x =`b с произвольной матрицей A. Исследуем вопрос о ее совместности и количестве решений.
ТЕОРЕМА КРОНЕКЕРА – КАПЕЛЛИ.
Для того, чтобы система уравнений A`x =`b была совместной, необходимо и достаточно, чтобы ранг матрицы этой системы равнялся рангу ее расширенной матрицы.
1) Пусть система уравнений A`x =`b является совместной. Докажем, что ранг r A матрицы A равняется рангу r à расширенной матрицы Ã.
Представим матрицы A и Ã как системы их векторов столбцов
соответственно. Ранг матрицы A равен рангу системы векторов (1), а ранг матрицы Ã равен рангу системы векторов (2). Поскольку система векторов (1) является подсистемой системы векторов (2), то r A £ r Ã.
Так как система A`x =`b является совместной, то существует вектор `x * = 
`A 1,`A 2 , … ,`A n ,`b Î L (`A 1,`A 2 , … ,`A n ). По свойствам ранга системы векторов r à £ r A. Но так как r A £ r à , то r A = r à .
2) Пусть теперь r A = r à = r. Докажем, что система A`x =`b является совместной. Согласно определению базиса системы векторов базисы систем (1) и (2) содержат по r векторов. Пусть`A 1, `A 2 , … ,`A r — базис системы (1). Тогда эти же векторы будут являться и базисом системы (2). Действительно, векторы`A 1,`A 2 , … ,`A r образуют линейно независимую подсистему системы (2), а поскольку их количество совпадает с рангом системы (2), то они являются базисом этой системы. Следовательно, вектор`b можно представить в виде линейной комбинации векторов`A 1,`A 2 , …,`A r :
`b = l 1`A 1 + l 2`A 2 + … + l r`A r, а также в виде линейной комбинации
`b = l 1`A 1 + l 2`A 2 + … + l r`A r + 0`A r + 1 + … + 0`A n. Справедливость последнего равенства означает, что вектор`x *, координатами которого являются числа l 1, l 2 , … , l r , 0, … , 0 является решением системы уравнений A`x =`b, то есть система A`x =`b совместна. Теорема доказана.
ТЕОРЕМА ОБ ОПРЕДЕЛЕННОСТИ СЛУ.
Пусть система уравнений A`x =`b является совместной, имеет n неизвестных и r A = r à = r.
Системы линейных уравнений с примерами решений
Содержание:
Системы уравнений, как и отдельные уравнения, используют для решения сложных и необходимых задач. Системы уравнений бывают с двумя, тремя и более переменными. В этой главе вы ознакомитесь с простейшими системами двух уравнений с двумя переменными. Основные темы лекции:
- уравнения с двумя переменными;
- график линейного уравнения;
- системы уравнений;
- способ подстановки;
- способ сложения;
- решение задач составлением системы уравнений.
Уравнения с двумя переменными
До сих пор мы рассматривали уравнение с одной переменной. Однако существуют задачи, решение которых приводит к уравнениям с двумя переменными.
Пример:
На 22 руб. купили несколько книжек по 5 руб. и географических карт — по 3 руб. Сколько купили книжек и карт?
Решение:
Пусть купили х книжки у карт. За книжки заплатили 5х руб., а за карты — 3у руб. Всего заплатили 22 руб., то есть, 5х + Зу = 22.
Это уравнение с двумя переменными. Приведём и другие примеры таких уравнений с двумя переменными:
Уравнение вида ах + by = с, где а, b, с — данные числа, называется линейным уравнением с двумя переменными х и у. Если
Примеры линейных уравнений:
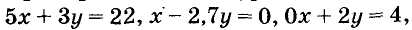
Паре чисел х = -1 и у = 9 удовлетворяет уравнение 5х + Зу -= 22, так как 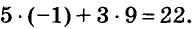
Каждая пара чисел, удовлетворяющая уравнение с двумя переменными, т. е. обращающая это уравнение в верное равенство, называется решением этого уравнения.
Обратите внимание: одно решение состоит из двух чисел, на первом месте записывают значение х, на втором — у. Корнями их не называют.
Чтобы найти решение уравнения с двумя переменными, следует подставить в уравнение произвольное значение первой неременной и, решив полученное уравнение, найти соответствующее значение второй переменной.
Для примера найдем несколько решений уравнения
Если х = 1, то 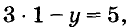
Уравнение 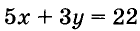
Два уравнения с двумя переменными называют равносильными, если каждое из них имеет те же решения, что и другое. Уравнения, не имеющие решений, также считаются равносильными.
Для уравнения с двумя переменными остаются справедливыми свойства, сформулированные для уравнений с одной переменной.
Обе части уравнения с двумя переменными можно умножить или разделить на одно и то же число, отличное от нуля. Любой член такого уравнения можно перенести из одной части уравнения в другую, изменив его знак на противоположный. В результате получается уравнение, равносильное данному.
Например, уравнение 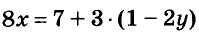
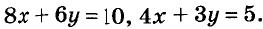
Иногда возникает потребность решить уравнение с двумя переменными во множестве целых чисел, то есть определить решения, являющиеся парами целых чисел. Способы решения таких уравнений определил древнегреческий математик Диофант (III в.), поэтому их называют диофантовыми уравнениями. Например, задача о книжках и картах сводится к уравнению 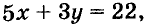
Переменную у из этого уравнения выразим через х:
Будем подставлять в равенство вместо х первые натуральные числа до тех пор, пока не получим целое значение переменной у. Это можно делать устно. Если х = 2, то у = 4. Других натуральных решений уравнение не имеет. Поэтому задача имеет единственное решение: 2 книги и 4 карты.
Пример:
Решение:
а) При любых значениях х и у значения выражения 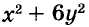
б) Значение выражения 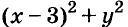
Пример:
Составьте уравнение с двумя переменными, решением которого будет пара чисел (1; -5).
Решение:
Пишем любой двучлен с переменными х и у, например 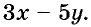
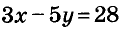
Есть много других линейных уравнений с двумя переменными, имеющих такое же решение (1; -5).
График линейного уравнения с двумя переменными
Рассмотрим уравнение 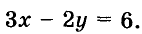
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://pandia.ru/text/78/164/88967-4.php
http://www.evkova.org/sistemyi-linejnyih-uravnenij