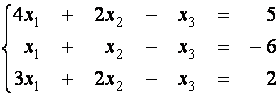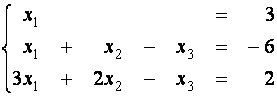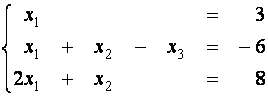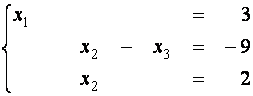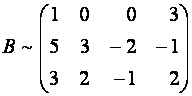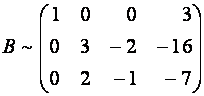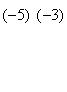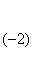Системой m линейных уравнений с n неизвестными называется

Системой m линейных уравнений с n неизвестными называется

Системой m линейных уравнений с n неизвестными называется система вида

где a_ij и b_i (i=1,…,m; b=1,…,n) – некоторые известные числа, а x₁,…,x_n – неизвестные. В обозначении коэффициентов a_ij первый индекс iобозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы , которую назовём матрицей системы.

Числа, стоящие в правых частях уравнений, b₁,…,b_m называются свободными членами.

Совокупность n чисел c₁,…,c_n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c₁,…,c_n вместо соответствующих неизвестных x₁,…,x_n.

Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:

1. Система может иметь единственное решение.
2. Система может иметь бесконечное множество решений. Например, . Решением этой системы является любая пара чисел, отличающихся знаком.
3. И третий случай, когда система вообще не имеет решения. Например, , если бы решение существовало, то x₁ + x₂ равнялось бы одновременно нулю и единице.

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.

Рассмотрим способы нахождения решений системы.

МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:

Рассмотрим матрицу системы и матрицы столбцы неизвестных и свободных членов

т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

или короче A∙X=B.

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.

Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A -1 , обратную матрице A: . Поскольку A -1 A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A -1 B.

Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A -1 B.

Примеры. Решить системы уравнений.

Найдем матрицу обратную матрице A.

,

Таким образом, x = 3, y = – 1.

Решите матричное уравнение: XA+B=C, где

Выразим искомую матрицу X из заданного уравнения.

Найдем матрицу А -1 .

Решите матричное уравнение AX+B=C, где

Из уравнения получаем .

Следовательно,

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:

Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,

называется определителем системы.

Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов

Тогда можно доказать следующий результат.

Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём

Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A₁₁ элемента a₁₁, 2-ое уравнение – на A₂₁ и 3-е – на A₃₁:

Сложим эти уравнения:

Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца

.

Далее рассмотрим коэффициенты при x₂:

Аналогично можно показать, что и .

Наконец несложно заметить, что

Таким образом, получаем равенство: .

Следовательно, .

Аналогично выводятся равенства и , откуда и следует утверждение теоремы.

Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.

Примеры. Решить систему уравнений

Решите систему уравнений при различных значениях параметра p:

Система имеет единственное решение, если Δ ≠ 0.

. Поэтому .

1. При
2. При p = 30 получаем систему уравнений которая не имеет решений.
3. При p = –30 система принимает вид и, следовательно, имеет бесконечное множество решений x=y,y Î R.

Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.

Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

.

Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x₁. Для этого второе уравнение разделим на а₂₁ и умножим на –а₁₁, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а₃₁ и умножим на –а₁₁, а затем сложим с первым. В результате исходная система примет вид:

Теперь из последнего уравнения исключим слагаемое, содержащее x₂. Для этого третье уравнение разделим на , умножим на и сложим со вторым. Тогда будем иметь систему уравнений:

Отсюда из последнего уравнения легко найти x₃, затем из 2-го уравнения x₂ и, наконец, из 1-го – x₁.

При использовании метода Гаусса уравнения при необходимости можно менять местами.

Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:

и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.

К элементарным преобразованиям матрицы относятся следующие преобразования:

1. перестановка строк или столбцов;
2. умножение строки на число, отличное от нуля;
3. прибавление к одной строке другие строки.

Примеры: Решить системы уравнений методом Гаусса.

Вернувшись к системе уравнений, будем иметь

Выпишем расширенную матрицу системы и сведем ее к треугольному виду.

Вернувшись к системе уравнений, несложно заметить, что третье уравнения системы будет ложным, а значит, система решений не имеет.

Разделим вторую строку матрицы на 2 и поменяем местами первый и третий столбики. Тогда первый столбец будет соответствовать коэффициентам при неизвестной z, а третий – при x.

Вернемся к системе уравнений.

Из третьего уравнения выразим одну неизвестную через другую и подставим в первое.

Таким образом, система имеет бесконечное множество решений.

Каждое уравнение системы можно записать в более компактной форме

,

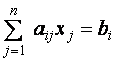
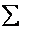
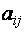
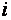
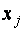
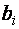
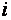
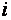
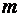
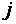
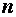
где — знак суммирования, — коэффициент в — ом уравнении при неизвестной , — свободный член — ого уравнения; при этом изменяется от 1 до , а — от 1 до .

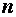
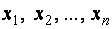
Упорядоченная совокупность чисел , которые при подстановке вместо неизвестных обращают каждое из уравнений системы (1) в верное числовое равенство, называется решением системы (1).

Другими словами: решением системы (1) является некоторый вектор .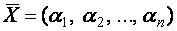

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной, не имеющая ни одного решения, называется несовместной.

Совместная система линейных уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Две системы линейных уравнений с одними и теми же неизвестными называются равносильными, или эквивалентными, если каждое решение одной системы является решением другой системы, и наоборот (или если обе системы несовместны).

Элементарными преобразованиями системы (1) будем называть преобразования вида:

1. Перестановка любых двух уравнений;

2. Умножение какого-либо уравнения на число, отличное от нуля;

3. Прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на одно и то же число, отличное от нуля;

4. Отбрасывание уравнения, все коэффициенты которого и свободный член равны нулю.

Справедливо следующее утверждение.

Ø При элементарных преобразованиях система (1) переходит в равносильную ей систему.

Приведем пример решения системы линейных уравнений с помощью элементарных преобразований.

Пример 1 . Решите с помощью элементарных преобразований следующую систему линейных уравнений

.

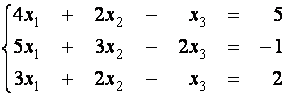
Будем использовать для обозначения эквивалентности систем уравнений знак Û .

(первое уравнение умножим на (-1) и прибавим ко второму)

(третье уравнение умножим на (-1) и прибавим к первому)

(второе уравнение умножим на (-1) и прибавим к третьему)

(первое уравнение умножим на (-1) и прибавим ко второму, а затем умножим его же на (-2) и прибавим к третьему)

(третье уравнение умножим на (-1) и прибавим ко второму)

(второе уравнение умножим на (-1) и после этого переставим с третьим)

.

Мы привели исходную систему к виду, разрешенному относительно неизвестных, откуда .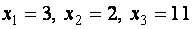

,

.

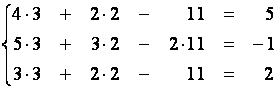
Получили три верные числовые равенства.

Итак, искомое решение 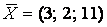, то есть исходная система оказалась совместной и определенной.

Анализируя процесс решения системы, сделаем несколько наблюдений.

1. В каждом уравнении преобразованной системы содержится ровно одна неизвестная (а остальные исключены), но четкого плана ее получения не видно.

2. Преобразованная система содержит 3 уравнения – столько же, сколько и исходная. Технически это понятно, так как использовались только три первые из элементарных преобразований, а четвертое применять не потребовалось.

3. В процессе преобразований уравнений системы фактически изменялись только ее коэффициенты и свободные члены.

Метод последовательного исключения неизвестных принадлежит великому немецкому математику Карлу Фридриху Гауссу (1777-1855) и, естественно, носит его имя.

Этот метод был усовершенствован известным французским математиком Камилем Мари Эдмоном Жорданом (1838-1922) и в новом виде стал называться методом Жордана-Гаусса .

Мы рассмотрим последовательно оба метода: метод Гаусса и метод Жордана-Гаусса .

В плане использования третьего наблюдения введем понятие матрицы.

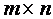
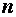
Матрицей размера будем называть прямоугольную таблицу, состоящую из чисел и имеющую строк и столбцов.

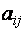
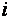
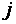
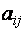
Числа, входящие в матрицу, принято называть ее элементами и обозначать , где индекс означает номер строки, а индекс — номер столбца матрицы, на пересечении которых стоит данный элемент .

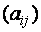
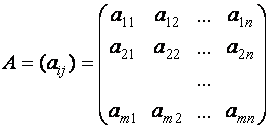
Сама матрица сокращенно обозначается символом или просто заглавной буквой:

.

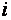
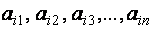
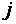
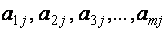
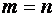
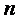
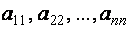
При этом — ая строка состоит из элементов , а — ый столбец – из элементов . При матрицу будет называть квадратной порядка . Для квадратной матрицы вводится понятие главной диагонали, состоящей из элементов .

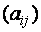
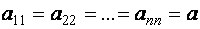
Матрица , у которой все элементы вне главной диагонали равны нулю, называется диагональной, а в случае — скалярной матрицей.

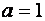
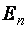
Скалярная матрица при называется единичной и обозначается или просто (когда порядок матрицы фиксирован).

Треугольной будем называть квадратную матрицу, все элементы которой ниже (или выше) главной диагонали равны нулю.

Ступенчатой матрицей назовем матрицу, в которой каждая строка, кроме первой, начинается с нулей, причем их число возрастает с ростом номера строки, но последняя строка содержит по крайней мере один ненулевой элемент.

Примерами ступенчатой матрицы могут служить матрицы

, ,

, .

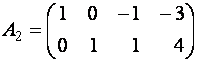
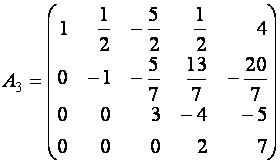
Заметим, что треугольная матрица является частным случаем ступенчатой. Примером треугольной матрицы служит матрица .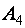

Теперь мы можем установить соответствие между системами линейных уравнений и матрицами.

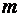
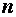
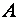
Для каждой системы (1) линейных уравнений с неизвестными можно составить матрицу из коэффициентов этой системы

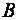
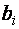
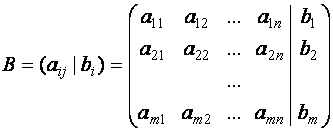
и матрицу из коэффициентов системы и ее свободных членов :

.

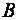
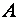
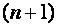
Таким образом, матрица отличается от матрицы наличием еще одного ( — ого) столбца – столбца свободных членов.

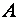
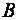
Матрицу принято называть матрицей системы (1), а матрицу — расширенной матрицей системы.

С другой стороны, имея матрицу 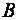, всегда можно записать соответствующую систему линейных уравнений (1).

В полной аналогии с элементарными преобразованиями системы линейных уравнений введем элементарные преобразования строк матрицы:

1. Перестановка любых двух строк;

2. Умножение любой строки на число, отличное от нуля;

3. Прибавление к одной строке другой строки, умноженной на число, отличное от нуля;

4. Выбрасывание нулевой строки.

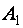
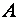
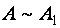
Если матрица получена из матрицы с помощью одного или нескольких (цепочки) элементарных преобразований, то такие матрицы принято называть эквивалентными и обозначать этот факт .

С помощью элементарных преобразований строк любую (ненулевую) матрицу можно привести к ступенчатому (в частности, треугольному) виду.

Покажем это на примере.

Пример 2 . Приведите к ступенчатому виду матрицу

Матрица 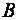является целочисленной, т.е. все ее элементы целые числа. В первом столбце нет элементов ± 1 (а именно такие элементы очень удобны для элементарных преобразований, что будет видно из дальнейшего).

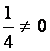
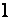
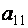
Можно было бы первую строку умножить на , создавая на месте элемента , но это приведет к потере целочисленности матрицы и поэтому к относительно неудобным последующим вычислениям.

Поступим иначе: умножим третью строку на 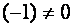и прибавим к первой, тогда

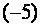
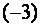
Теперь (для создания нулей в первом столбце) умножим первую строку новой матрицы на и прибавим ко второй, а после умножения ее же на прибавим к третьей строке.

Умножим третью строку полученной матрицы на 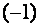и прибавим ко второй:

Умножим вторую строку на 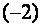и прибавим к третьей:

Матрица 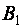— ступенчатая.

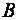
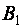
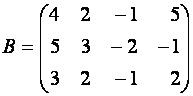
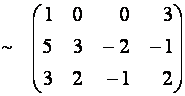
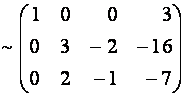
Цепочку преобразований матрицы к ступенчатой матрице можно записать следующим образом:

.

Замечание. Можно ввести понятие элементарных преобразований и для столбцов матрицы.

Системы m линейных уравнений с n неизвестными. Определение: Определение. Система m уравнений с n неизвестными в общем виде записывается следующим образом: — презентация

Презентация была опубликована 7 лет назад пользователемДиана Авлова

Похожие презентации

Презентация на тему: » Системы m линейных уравнений с n неизвестными. Определение: Определение. Система m уравнений с n неизвестными в общем виде записывается следующим образом:» — Транскрипт:

1 Системы m линейных уравнений с n неизвестными

2 Определение: Определение. Система m уравнений с n неизвестными в общем виде записывается следующим образом: Определение. Система m уравнений с n неизвестными в общем виде записывается следующим образом:, где a ij – коэффициенты, а b i – постоянные. где a ij – коэффициенты, а b i – постоянные.

3 Решениями системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество. Решениями системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество.

4 Основные определения Определение. Если система имеет хотя бы одно решение, то она называется совместной. Если система не имеет ни одного решения, то она называется несовместной. Определение. Система называется определенной, если она имеет только одно решение и неопределенной, если более одного.

5 Основные определения Определение. Для системы линейных уравнений матрица Определение. Для системы линейных уравнений матрица А = называется матрицей системы

6 Основные определения Матрица Матрица А= А= называется расширенной матрицей системы называется расширенной матрицей системы

7 Основные определения Определение. Определение. Если b 1, b 2, …,b m = 0, то система называется однородной. Однородная система всегда совместна, т.к. всегда имеет нулевое решение. Однородная система всегда совместна, т.к. всегда имеет нулевое решение.

8 Элементарные преобразования матриц К элементарным преобразованиям относятся: К элементарным преобразованиям относятся: 1)Прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на одно и то же число, не равное нулю. 1)Прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на одно и то же число, не равное нулю. 2)Перестановка уравнений местами. 2)Перестановка уравнений местами. 3)Удаление из системы уравнений, являющихся тождествами для всех х. 3)Удаление из системы уравнений, являющихся тождествами для всех х.

9 Элементарные преобразования матрицы: — перестановка строк (перенумерация уравнений) — перестановка столбцов основной матрицы (перенумерация неизвестных); — удаление нулевой строки (исключение уравнений, тождественно удовлетворяющихся любыми значениями неизвестных); — умножение строки на ненулевое число (нормирование уравнений); — сложение строки с линейной комбинацией остальных строк с записью результата на место исходной строки (замена одного из уравнений системы следствием ее уравнений, получаемым при помощи линейных операций).

10 Замечание: Решение неоднородной системы уравнений (равно как и ее ранг) не изменится также и при использовании любой комбинации элементарных операций. Решение неоднородной системы уравнений (равно как и ее ранг) не изменится также и при использовании любой комбинации элементарных операций.

11 Теорема Кронекера – Капелли. (условие совместности системы) Теорема: Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы. Теорема: Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы. RgA = RgA*.

12 Пример: Определить совместность системы линейных уравнений: Ответ: Система несовместна Ответ: Система несовместна

13 Матричная запись систем линейных уравнений. Пусть дана система уравнений: Пусть дана система уравнений: Составим матрицы: Составим матрицы: A = В = Х =

14 Систему можно записать в матричном виде: A X = B Определение Определение Упорядоченный набор чисел называется частным решением системы линейных уравнений, если при подстановке этих чисел в систему мы получаем верные равенства.. Совокупность всех частных решений системы линейных уравнений назовем общим решением системы

15 Фундаментальная система решений Рассмотрим случай, когда система совместна и найдем все ее решения. Рассмотрим случай, когда система совместна и найдем все ее решения.

16 Вспомогательные утверждения Любая линейная комбинация частных решений однородной системы также является ее частным решением. Любая линейная комбинация частных решений однородной системы также является ее частным решением. Сумма некоторого частного решения однородной системы и некоторого частного решения неоднородной системы является частным решением неоднородной системы Сумма некоторого частного решения однородной системы и некоторого частного решения неоднородной системы является частным решением неоднородной системы Разность двух некоторых частных решений неоднородной системы является частным решением однородной системы. Разность двух некоторых частных решений неоднородной системы является частным решением однородной системы.

17 Из указанных утверждений следует: Общее решение неоднородной системы уравнений есть общее решение однородной плюс некоторое частное решение неоднородной Общее решение неоднородной системы уравнений есть общее решение однородной плюс некоторое частное решение неоднородной

18 Теорема: Однородная система имеет Однородная система имеет линейно независимых частных решений.

19 Определение: Фундаментальной системой решений для системы линейных уравнений называется совокупность Фундаментальной системой решений для системы линейных уравнений называется совокупностьлюбых частных, линейно независимых решений соответствующей однородной системы, где — n число неизвестных в системе.), а — ее основная матрица.

20 Матрица называется фундаментальной.

21 Теорема: Каждое частное решение однородной системы может быть представлено в виде линейной комбинации частных решений, образующих нормальную фундаментальную систему решений. Каждое частное решение однородной системы может быть представлено в виде линейной комбинации частных решений, образующих нормальную фундаментальную систему решений.

22 Следствие Общее решение неоднородной системы может быть дано формулой Общее решение неоднородной системы может быть дано формулой

23 где является некоторым частным решением неоднородной системы, где является некоторым частным решением неоднородной системы, а числа произвольные константы

24 Следствие Для того чтобы однородная система с имела ненулевое решение, необходимо и достаточно, чтобы ранг ее основной матрицы удовлетворял условию Для того чтобы однородная система с имела ненулевое решение, необходимо и достаточно, чтобы ранг ее основной матрицы удовлетворял условию В частном случае, когда основная матрица системы квадратная, условие существования нетривиального решения равносильно равенству В частном случае, когда основная матрица системы квадратная, условие существования нетривиального решения равносильно равенству

25 Метод Гаусса Суть этого метода заключается в приведении расширенной матрицы системы линейных уравнений к наиболее простому виду последовательностью так называемых элементарных преобразований, каждое из которых не меняет общего решения системы уравнений. Суть этого метода заключается в приведении расширенной матрицы системы линейных уравнений к наиболее простому виду последовательностью так называемых элементарных преобразований, каждое из которых не меняет общего решения системы уравнений.

26 С помощью элементарных преобразований привести матрицу системы к следующему виду:

27 Задача: Решить систему уравнений

28 1. Составляем расширенную матрицу системы

29 2. Приводим ее к верхнему треугольному виду.

30 3. Полученная матрица является расширенной матрицей системы линейных уравнений, равносильной исходной системе. Ранг этой матрицы совпадает с рангом исходной. Потому заключаем, что а) система совместна, поскольку ранг основной матрицы равен рангу расширенной и равен 2 (по теореме Кронекера-Капелли); б) однородная система уравнений будет иметь линейно независимых решения.

31 4. Поскольку общее решение неоднородной системы есть общее решение однородной плюс частное решение неоднородной, то нам достаточно найти три любых линейно независимых решения однородной системы и какое-нибудь одно решение неоднородной. Перепишем исходную систему в преобразованном виде, приняв первое и второе неизвестные за основные, а третье, четвертое и пятое — за свободные. Перепишем исходную систему в преобразованном виде, приняв первое и второе неизвестные за основные, а третье, четвертое и пятое — за свободные. Второе уравнение для удобства вычислений умножим на -1, а третье и четвертое уравнения отбросим как удовлетворяющиеся тождественно. Второе уравнение для удобства вычислений умножим на -1, а третье и четвертое уравнения отбросим как удовлетворяющиеся тождественно.

32 находим частное решение неоднородной системы Значения основных неизвестных определяются системы линейных уравнений

33 Для однородной системы строим нормальную фундаментальную систему решений строим нормальную фундаментальную систему решений

34 Первое независимое решение находится из системы

35 Аналогично получаются второе и третье решения:

36 Замечание: поскольку существует свобода выбора как частного решения неоднородной системы, так и линейно независимых решений однородной, то общее решение неоднородной системы может быть записано в различных, но, естественно, равносильных формах.