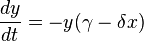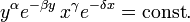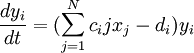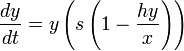Систему дифференциальных уравнений лотки вольтерра

Систему дифференциальных уравнений лотки вольтерра

Дифференциальные уравнения широко используются для моделирования реальных систем, зависящих от времени, в частности, для описания и исследования экономических и биологических систем.

В динамике популяций есть много примеров, когда изменение численности популяций во времени носит колебательный характер. Одним из самых известных примеров описания динамики взаимодействующих популяций являются уравнения Вольтерра—Лотка. Рассмотрим модель взаимодействия хищников и их добычи, когда между особями одного вида нет соперничества.
Пусть x₁ и x₂ — число жертв и хищников соответственно. Предположим, что относительный прирост жертв x₁‘/x₁ равен a-bx₂, a>0, b>0, где a — скорость размножения жертв в отсутствие хищников, —bx₂ — потери от хищников. Развитие популяции хищников зависит от количества пищи (жертв), при отсутствии пищи ( x₁=0 ) относительная скорость изменения популяции хищников равна , c>0 , наличие пищи компенсирует убывание, и при x1>0 имеем , d>0.
Таким образом, система Вольтерра—Лотка имеет вид:

где a, b, c, d >0.
Рассмотренная модель может описывать поведение конкурирующих фирм, рост народонаселения, численность воюющих армий, изменение экологической обстановки, развитие науки и пр.
Рассмотрим фазовый портрет системы Вольтерра—Лотка для a=4, b=2.5, c=2, d=1 и графики ее решения с начальным условием x₁(0)=3, x₂(0)=1, построенные программой ОДУ.

Видно, что процесс имеет колебательный характер. При заданном начальном соотношении числа особей обоих видов 3 : 1 , обе популяции сначала растут. Когда число хищников достигает величины b=2.5 , популяция жертв не успевает восстанавливаться и число жертв начинает убывать. Уменьшение количества пищи через некоторое время начинает сказываться на популяции хищников и когда число жертв достигает величины x₁=c/d =2 (в этой точке x₂‘=0), число хищников тоже начинает сокращаться вместе с сокращением числа жертв. Сокращение популяций происходит до тех пор, пока число хищников не достигнет величины x₂=a/b =1.6 (в этой точке x₁‘=0).С этого момента начинает расти популяция жертв, через некоторое время пищи становится достаточно, чтобы обеспечить прирост хищников, обе популяции растут, и . процесс повторяется снова и снова. На графике четко виден периодический характер процесса. Количество жертв и хищников колеблется возле величин x₁=2, x₂=1.6 соответственно (дробные числа здесь не означают “половину волка”, величины могут измеряться в сотнях, тысячах и т.п.). Периодичность процесса явственно видна на фазовой плоскости — фазовая кривая (x₁(t), x₂(t)) — замкнутая линия. Самая левая точка, этой кривой, — это точка, в которой число жертв достигает наименьшего значения. Самая правая точка x₁=4, x₂=1.6 , — точка пика популяции жертв. Между этими точками количество хищников сначала убывает, до нижней точки фазовой кривой,x₁=2 , где достигает наименьшего значения, а затем растет до верхней точки фазовой кривой (x₁=2, x₂=2.5). Фазовая кривая охватывает точку x₁=2, x₂=1.6.
На языке дифференциальных уравнений это означает, что система имеет стационарное состояние
x₁‘ =0, x₂‘ =0,
которое достигается в точке x₁=2, x₂=1.6. Если в начальный момент система находилась в стационарной точке, то решения x₁(t), x₂(t) не будут изменяться во времени, останутся постоянными. Всякое же другое начальное состояние приводит к периодическому колебанию решений. Неэллиптичность формы траектории, охватывающей центр, отражает негармонический характер колебаний.

Рассмотренная модель может описывать поведение конкурирующих фирм, рост народонаселения, численность воюющих армий, изменение экологической обстановки, развитие науки и т.п.

Рассмотрим модель конкурирующих видов с “логистической поправкой”:

В этом случае поведение решений в окрестности стационарной точки меняется в зависимости от величины и знака параметра a.
Рассмотрим фазовый портрет системы Вольтерра—Лотка для a =0.1, a=4, b=2.5, c=2, d=1 и графики ее решения с начальным условием x₁(0)=3, x₂(0)=1, построенные программой ОДУ.

Видно, что в этом случае стационарная точка превращается в устойчивый фокус, а решения — в затухающие колебания. При любом начальном условии состояние системы через некоторое время становится близким к стационарному и стремится к нему при .

Графики решений и фазовая кривая при отрицательном значении параметра a, a =-0.1, приведены ниже.

Как видно, в этом случае стационарная точка является неустойчивым фокусом и амплитуда колебаний численности видов растет. В этом случае как бы близко ни было начальное состояние к стационарному, с течением времени состояние системы будет сильно отличаться от стационарного.

ПРИМЕР 2. Модель «хищник-жертва» с логистической поправкой.

На примере модели Вольтерра—Лотка и модели Вольтерра—Лотка с логистической поправкой было продемонстрировано одно из важнейших качественных свойств центров — они легко разрушаются даже при самых малых изменениях правой части. Большинство моделей является идеализацией действительности; в них внимание сосредоточено на некоторых основных переменных и соотношениях между ними. Поэтому устойчивость моделей относительно малых возмущений чрезвычайно важна в приложениях. Модели, не чувствительные к малым возмущениям, называются грубыми.

Модель Вольтерра—Лотка неустойчива относительно возмущений, поскольку ее стационарное состояние — центр.

Существует другой вид моделей, в которых возникают незатухающие колебания, — это модели, имеющие на фазовых портретах предельные циклы. Такая модель существует для системы конкурирующих видов — это модель Холлинга—Тэннера.
Скорость роста популяции жертв x‘₁ в этой модели равна сумме трех величин:

• скорости размножения в отсутствие хищников — r x₁;
• влиянию межвидовой конкуренции за пищу при ограниченных ресурсах (для случая конкурирующих производителей это влияние ограниченных сырьевых ресурсов) —
• влиянию хищников , в предположении, что хищник перестает убивать, когда насыщается —

Скорость роста популяции хищников x‘₂ строится так же, как в модели Вольтерра—Лотка, в предположении, что жертвы встречаются редко. Если для поддержания жизни одного хищника нужно J жертв, то популяция из x₁ жертв сможет обеспечить пищей x₁/J хищников. Модель роста популяции хищников, в которой их число не может превысить эту критическую величину, имеет вид
.
Таким образом, имеем модель Холлинга—Тэннера:

где r, s, K, D, J > 0.
Можно показать, что при

на фазовом портрете системы будет устойчивый предельный цикл. Ниже приведено решение системы при r=1, K=7, w=1, D=1, s=0.2, J=0.5 и двух различных начальных состояниях и фазовый портрет системы, построенные программой ОДУ.

Модель выравнивания цен по уровню актива интересна тем, что в ней можно наблюдать гармонические колебания решений возле стационарного состояния. Предположим, что изменение уровня актива q пропорционально разности между предложением s и спросом d, т.е. q‘=k(s—d), k > 0. Предположим далее, что изменение цены p пропорционально отклонению актива q от некоторого фиксированного уровня q₀ так, что p‘=-m(q—q₀ ) , m > 0. Таким образом, модель выравнивания цен по уровню актива имеет вид
q‘ = k(s(p) — d(p)),
p‘ = — m(q—q₀).

Видно, что цена и актив колеблются возле стационарного состояния. Фазовая траектория представляет собой эллипс, охватывающий стационарную точку. Это означает, что колебания актива и цены — гармонические.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Я догоняю, ты убегаешь

Что такое модель Лотки-Вольтерры и как она помогает биологам

Могут ли сложные математические инструменты применяться в биологии? Могут, если биологи изучают сложные динамические системы, например взаимодействие разных видов животных в естественной среде. Американец Альфред Лотка и итальянец Вито Вольтерра разработали модель, позволяющую описывать, как будет меняться поголовье хищников и их травоядных жертв в зависимости от множества привходящих условий. Это наш второй материал о самых интересных дифференциальных уравнениях (с первым можно ознакомиться здесь). Если вы читаете нас с телефона, переключайте страницу на десктопную версию, так вы сможете увидеть интерактивный график целиком.

Изначально Альфред Лотка вообще не планировал создавать никаких математических моделей. Он собирался разработать новую предметную область — «физическую биологию» — и поэтому начиная с 1902 года стал публиковать небольшие статьи, посвященные этой теме.

Параллельно с этим его все более интересовало применение математических методов в биологии. Идеи Лотки, однако, не получили широкого распространения — в то время американский ученый не имел широких связей в научной среде и работал в одиночестве.

Ситуация изменилась в 1920 году, когда статьи Лотки привлекли внимание биолога и статистика Раймонда Пирла, который нашел в них близкие для себя идеи: Пирл интересовался ростом популяции в пределах одного вида.

Лотка написал еще одну статью, и Пирл помог продвинуть ее в Proceedings of the National Academy of Sciences (ведущий американский журнал для публикации оригинальных научных исследований в различных областях). В этой статье Лотка в качестве примера описал взаимодействие растения и травоядного и пришел к неожиданному для него результату: их взаимодействие приведет к бесконечному циклическому колебанию в двух популяциях!

Позже Лотка расширил это наблюдение до общего случая взаимодействия типа «хищник-жертва».

Итальянский ученый Вито Вольтерра, как и Альфред Лотка, пришел к этой модели со стороны точных наук. Он с раннего детства питал тягу к математике и занимался ею всю свою жизнь, и уже в 1900-е годы заинтересовался возможностью использовать математику в биологии и общественных науках.

После окончания Первой мировой войны Вольтерра погрузился в биологию и, сам того не зная, пришел к выводам, схожим с выводами Альфреда Лотки, сделанными ранее. Однако именно работы Вольтерры привлекли внимание математического сообщества.

В итоге Вольтерра, чья статья вышла в 1926 году, признал приоритет Лотки. Но чтобы его собственные работы не выглядели бессмысленными, Вольтерра отметил, что рассмотрел ситуацию в более общем случае: вывел уравнения, которые описывают взаимодействие более чем двух видов и учитывают их контакт в прошлом.

Модель Лотки-Вольтерры

Система Лотки-Вольтерры является первоначальной и простейшей системой (усложненные системы будут рассмотрены ниже) для описания модели «хищник-жертва», то есть популяции хищников и популяции жертв, взаимодействующих в какой-то среде: жертвы едят растительность, хищники — жертв:

Уравнения Лотки-Вольтерры

Уравнения Лотки — Вольтерры или уравнения хищник — жертва — система двух обыкновенных дифференциальных уравнений первого порядка, описывающей кинетику численности популяции с одним типом хищников и одним типом жертв. Характерной особенностью ривннянь является то, что их решением является автоколебания. Уравнение предложили независимо Альфред Джеймс Лотка и Вито Вольтерра, в 1925 и 1926 годах, соответственно.

Уравнения имеют вид

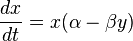
где x — количество жертв, например, зайцев, y — количество хищников, например, волков, — определенные параметры.

В уравнение входят следующие процессы: размножение жертв и их гибель в результате поедания хищниками, размножения и вымирания хищников. Считается, что размножение хищников пропорционально количеству пищи, то есть, количества потенциальных жертв в популяции.

Стационарные точки

Система уравнение имеет два стационарные точки:

1. x = 0, y = 0 — эта точка соответствует отсутствию в популяции как жертв, так и хищников.

Анализ устойчивости стационарных точек показывает, что первая из них (нулевая) является седловой, а вторая — фокусом. Показатель Ляпунова для фокуса чисто мысленный, поэтому с линейного анализа сделать вывод об устойчивости или неустойчивости фокуса невозможно. Однако для уравнений Лотка-Вольтерра существует интеграл движения, показывает, что фазовые траектории — замкнутые кривые, внутри которых находится фокус.

Интеграл движения

Для решения уравнения Лотки-Вольтерра существует интеграл движения

Типичные фазовые траектории показаны на рисунке справа. При значительном размножении жертв создаются условия для размножения хищников благодаря доступности пищи. Но размножения хищников приводит к уменьшению числа жертв. Когда число жертв сильно падает, хищники тоже погибают из-за недостатка пищи. Только тогда, когда количество хищников достигает минимума, популяция жертв снова начинает расти.

Существование интеграла движения приводит к тому, что величины популяций определяются начальными условиями. В этой задач не предельного цикла, который был бы аттракторов для фазовых траекторий. Циклы в задачи хищник-жертва имеют равнодушную устойчивость.

Обобщенная модель Лотки-Вольтерры

Модель Лотки-Вольтерра может быть обобщена для многих популяций (N). Для них мы имеем такие уравнения:

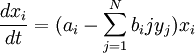
где параметры имеют такой же смысл как в модели с двумя видами организмов.

Реалистичная модель «хищник-жертва»

Главный недостаток модели Лотки-Вольтерры заключается в том, что при нулевой численности хищников популяция жертв неограниченно растет. Таким образом, в реалистичных моделях, описывающих это явление должно быть пропускная способность K — максимальное число лиц которой может достигать размер популяции. Уравнение учитывает этот фактор приведены ниже:

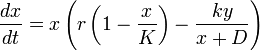
— Находятся в постоянной зависимости от модели.