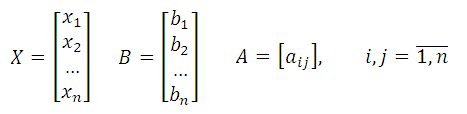Систему линейных алгебраических уравнений matlab

Как решить систему линейных уравнений в matlab

Решение системы линейных алгебраических уравнений (СЛАУ) средствами MATLAB

.

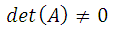
Систему уравнений (1) в MATLAB можно решить различными методами:

1. Использованием обратной матрицы.

Из (1) следует, что X = A -1 B. Данное выражение непосредственно вычисляется в MATLAB. Получить обратную матрицу можно с помощью функции inv(A), либо с помощью оператора A^-1 , что означает A в степени -1.

2. Решение системы уравнений методом Гаусса.

Метод исключения Гаусса является одним из наиболее простых и эффективных методов. Алгоритм метода Гаусса основан на приведении матрицы А к треугольному виду (прямой ход) и последовательном вычислении неизвестных (обратный ход). Эти процедуры можно выполнять над невыраженными матрицами, в противном случае метод Гаусса неприменим.

Недостатком метода является накапливание погрешностей в процессе округления, поэтому метод Гаусса без выбора главных элементов используется обычно для решения сравнительно небольших (n < 100 — 200) систем уравнений с плотно заполненной матрицей и не близким к нулю определителем.

В MATLAB для решения систем уравнений (1) методом исключения Гаусса применяются следующие операторы:

Решение СЛАУ и матрицы в Matlab

Доброго времени суток, читатели! Сегодня мы поговорим о матрицах в Matlab, об их применении в решении систем линейных алгебраических уравнений. Подробно разберем методы решения, и для этого необходимо знание нескольких базовых алгоритмов.

Также стоит отметить, что у каждого алгоритма, которым мы будем искать решение СЛАУ в Matlab, своя скорость нахождения этого решения, наличие или отсутствие условия выполнения алгоритма и т.д.

В традициях нашего сайта разберём на примере:

Решить систему линейных уравнений:

4*a + b — c = 6
a — b + c = 4
2*a — 3*b — 3*c = 4

Метод обратной матрицы в Matlab

Начнем с достаточно распространенного метода. Его суть состоит в том, что сначала необходимо выписать коэффициенты при a, b и c (то есть те коэффициенты, которые находятся слева) в одну матрицу, а свободный член (то есть то, что справа) в другую.

В итоге у нас получится 2 матрицы:

Для реализации этого метода (и следующих методов тоже) требуется одно условие: чтобы определитель матрицы, составленной из коэффициентов левой части не был равен нулю. Проверка на определитель:

После проверки условия можем перейти к следующему шагу: нахождение обратной матрицы. В Matlab для этого используется оператор inv .
А само решение СЛАУ в Matlab находится как перемножение найденной обратной матрицы на матрицу свободных членов:

Мы получили 3 значения, которые и соответствуют нашим коэффициентам: то есть a = 2, b = -1, c = 1 . Можете проверить, подставив полученные ответы в исходную систему, и убедиться, что мы решили СЛАУ правильно.

Также следует отметить, что матрицы нужно перемножать именно, как сделали мы, то есть слева обратная матрица, справа матрица свободных членов.

Если вы не все поняли, то советую вам почитать нашу статью по основам Matlab.

Метод Гаусса

Метод Гаусса в Matlab реализуется достаточно просто: для этого нам нужно всего лишь изучить один новый оператор.
(\) — левое деление.
При следующей записи:

Мы получим ответы на нашу исходную систему. Только заметьте, мы решили СЛАУ стандартным набором функций в Matlab, и желательно этот оператор использовать когда матрица коэффициентов квадратная, так как оператор приводит эту матрицу к треугольному виду. В других случаях могут возникнуть ошибки.

Метод разложения матрицы

Теперь поговорим о разложении матрицы. Нахождение решения через разложение матрицы очень эффективно. Эффективность обусловлена скоростью нахождения решения для данного вида систем и точностью полученных результатов.

Возможны следующие разложения:

• разложение Холецкого
• LU разложение
• QR разложение

Разберём решение через LU и QR разложение, так как в задачах чаще всего встречается задание на решение именно через такие разложения.

Основное отличие этих двух разложений: LU разложение применимо только для квадратных матриц, QR — возможно и для прямоугольных.

LU разложение

Решим выше предложенную задачу через LU разложение:

QR разложение

И через QR разложение соответственно:

Отметим, что апостроф ( ‘ ) после Q означает транспонирование.

Стандартные функции Matlab

Так же Matlab предлагает функцию linsolve , с помощью которой возможно решить систему линейных алгебраических уравнений. Выглядит это так:

Как видите, ничего сложного тут нет, на то они и стандартные функции Matlab.

Повторение

Итак, сегодня мы с вами изучили несколько методов для решения СЛАУ в Matlab, как с помощью матриц, так и с помощью стандартных функций. Давайте их повторим на другом примере:

Решить систему линейных уравнений:
6*a — b — c = 0
a — 2*b + 3*d = 0
3*a — 4*b — 4*c = -1

• Методом обратной матрицы:
• Методом Гаусса:
• LU разложение:
• QR разложение:

На этом я с вами попрощаюсь, надеюсь, вы научились применять матрицы в Matlab для решения СЛАУ.

Документация

Одной из самых важных проблем в техническом вычислении является решение систем одновременных линейных уравнений.

В матричном обозначении общая проблема принимает следующую форму: Учитывая две матрицы A и b, действительно там существует уникальный матричный x, так, чтобы A x = b или x A = b?

Это поучительно, чтобы рассмотреть пример 1 на 1. Например, делает уравнение

имеет уникальное решение?

Ответ, конечно, является да. Уравнение имеет уникальное решение x = 3. Решение легко получено делением:

Решение обычно не получается путем вычисления инверсии 7, который равняется 7 –1 = 0.142857. и затем умножение 7 –1 21. Это было бы, больше работают и, если 7 –1 представлен конечному числу цифр, менее точных. Подобные факторы применяются к наборам линейных уравнений с больше чем одним неизвестным; MATLAB ® решает такие уравнения, не вычисляя инверсию матрицы.

Несмотря на то, что это не стандартное математическое обозначение, MATLAB использует терминологию деления, знакомую в скалярном случае, чтобы описать решение общей системы одновременных уравнений. Два символа деления, наклонная черта ,/, и обратная косая черта , \, соответствуют этим двум функциям MATLAB mrdivide и mldivide . Эти операторы используются для двух ситуаций, где неизвестная матрица появляется слева или право на матрицу коэффициентов:

Обозначает решение матричного уравнения xA = b, полученное использование mrdivide .

Обозначает решение матричного уравнения Ax = b, полученное использование mldivide .

Думайте о “делении” обеих сторон уравнения Ax = b или xA = b A. Матрица коэффициентов A всегда находится в “знаменателе”.

Условия совместимости размерности для x = A\b потребуйте этих двух матриц A и b иметь одинаковое число строк. Решение x затем имеет одинаковое число столбцов как b и его размерность строки равна размерности столбца A . Для x = b/A , ролями строк и столбцов обмениваются.

На практике линейные уравнения формы Ax = b происходят более часто, чем те из формы xA = b. Следовательно, обратная косая черта используется намного более часто, чем наклонная черта. Остаток от этого раздела концентрируется на операторе обратной косой черты; соответствующие свойства оператора наклонной черты могут быть выведены из идентичности:

Матрица коэффициентов A не должно быть квадратным. Если A имеет размер m-by-n, затем существует три случая:

Квадратная система. Ищите точное решение.

Сверхрешительная система, большим количеством уравнений, чем неизвестные. Найдите решение методом наименьших квадратов.

Недоопределенная система, меньшим количеством уравнений, чем неизвестные. Найдите основное решение с в большей части m ненулевые компоненты.

Mldivide Алгоритм

mldivide оператор использует другие решатели, чтобы обработать различные виды содействующих матриц. Различные случаи диагностированы автоматически путем исследования матрицы коэффициентов. Для получения дополнительной информации смотрите раздел “Algorithms” mldivide страница с описанием.

Общее решение

Общее решение системы линейных уравнений Ax = b описывает все возможные решения. Можно найти общее решение:

Решение соответствующей гомогенной системы Ax = 0. Сделайте это использование null команда, путем ввода null(A) . Это возвращает базис для пробела решения к Ax = 0. Любое решение является линейной комбинацией базисных векторов.

Нахождение конкретного решения неоднородной системы Ax =b.

Можно затем записать любое решение Ax = b как сумма конкретного решения Ax =b, от шага 2, плюс линейная комбинация базисных векторов от шага 1.

Остальная часть этого раздела описывает, как использовать MATLAB, чтобы найти конкретное решение Ax =b, как на шаге 2.

Квадратные системы

Наиболее распространенная ситуация включает квадратную матрицу коэффициентов A и один правый вектор-столбец стороны b .

Невырожденная матрица коэффициентов

Если матричный A несингулярно, затем решение, x = A\b , одного размера с b . Например:

Можно проверить, что A*x точно равно u .

Если A и b являются квадратными и тот же размер, x= A\b также что размер:

Можно проверить, что A*x точно равно b .

Оба из этих примеров имеют точные, целочисленные решения. Это вызвано тем, что матрица коэффициентов была выбрана, чтобы быть pascal(3) , который является (несингулярной) матрицей полного ранга.

Сингулярная матрица коэффициентов

A квадратной матрицы сингулярен, если он не имеет линейно независимых столбцов. Если A сингулярен, решение Ax = b или не существует или не уникален. Оператор обратной косой черты, A\b , выдает предупреждение если A почти сингулярно или если это обнаруживает точную сингулярность.

Если A сингулярен и Ax =, b имеет решение, можно найти конкретное решение, которое не уникально путем ввода

pinv(A) псевдоинверсия A. Если Ax = b не имеет точного решения, то pinv(A) возвращает решение методом наименьших квадратов.

сингулярно, когда можно проверить путем ввода

Поскольку A не является полным рангом, он имеет некоторые равные нулю сингулярные значения.

Точные решения. Для b =[5;2;12] , уравнение Ax = b имеет точное решение, данное

Проверьте тот pinv(A)*b точное решение путем ввода

Решения методом наименьших квадратов. Однако, если b = [3;6;0] , Ax = b не имеет точного решения. В этом случае, pinv(A)*b возвращает решение методом наименьших квадратов. Если вы вводите

вы не возвращаете исходный вектор b .

Можно определить, имеет ли Ax =b точное решение путем нахождения, что строка уменьшала форму эшелона расширенной матрицы [A b] . Чтобы сделать так для этого примера, войти

Поскольку нижний ряд содержит все нули за исключением последней записи, уравнение не имеет решения. В этом случае, pinv(A) возвращает решение методом наименьших квадратов.

Сверхрешительные системы

В этом примере показано, как со сверхрешительными системами часто сталкиваются в различных видах аппроксимирования кривыми к экспериментальным данным.

Количество y измеряется в нескольких различных значениях времени t произвести следующие наблюдения. Можно ввести данные и просмотреть их в таблице со следующими операторами.

Попытайтесь моделировать данные с затухающей показательной функцией

y ( t ) = c 1 + c 2 e — t .

Предыдущее уравнение говорит что векторный y должен быть аппроксимирован линейной комбинацией двух других векторов. Каждый — постоянный вектор, содержащий все единицы, и другой вектор с компонентами exp(-t) . Неизвестные коэффициенты, c 1 и c 2 , может быть вычислен путем выполнения метода наименьших квадратов, который минимизирует сумму квадратов отклонений данных из модели. Существует шесть уравнений в двух неизвестных, представленных 6 2 матрица.

Используйте оператор обратной косой черты, чтобы получить решение методом наименьших квадратов.

Другими словами, метод наименьших квадратов к данным

y ( t ) = 0 . 4 7 6 0 + 0 . 3 4 1 3 e — t .

Следующие операторы оценивают модель в расположенном с равными интервалами шаге в t , и затем постройте результат вместе с исходными данными:

E*c не точно равно y , но различие может хорошо быть меньше погрешностей измерения в исходных данных.

Прямоугольный матричный A имеет неполный ранг, если это не имеет линейно независимых столбцов. Если A имеет неполный ранг, затем решение методом наименьших квадратов к AX = B не уникально. A\B выдает предупреждение если A имеет неполный ранг и производит решение методом наименьших квадратов. Можно использовать lsqminnorm найти решение X это имеет минимальную норму среди всех решений.

Недоопределенные системы

В этом примере показано, как решение недоопределенных систем не уникально. Недоопределенные линейные системы включают больше неизвестных, чем уравнения. Матричная операция левого деления в MATLAB находит основное решение методом наименьших квадратов, которое имеет в большей части m ненулевые компоненты для m — n матрица коэффициентов.

Вот небольшой, случайный пример:

Линейная система Rp = b вовлекает два уравнения в четыре неизвестные. Поскольку матрица коэффициентов содержит маленькие целые числа, уместно использовать format команда, чтобы отобразить решение в рациональном формате. Конкретное решение получено с

Одним из ненулевых компонентов является p(2) потому что R(:,2) столбец R с самой большой нормой. Другим ненулевым компонентом является p(4) потому что R(:,4) доминирует после R(:,2) устраняется.

Полное общее решение недоопределенной системы может быть охарактеризовано путем добавления p к произвольной линейной комбинации пустых векторов пробела, которые могут быть найдены с помощью null функция с опцией, запрашивающей рациональный базис.

Можно проверить, что R*Z нуль и что остаточный R*x — b мал для любого векторного x , где

Начиная со столбцов Z пустые векторы пробела, продукт Z*q линейная комбинация тех векторов:

Z q = ( x ⇀ 1 x ⇀ 2 ) ( u w ) = u x ⇀ 1 + w x ⇀ 2 .

Чтобы проиллюстрировать, выберите произвольный q и создайте x .

Вычислите норму невязки.

Когда бесконечно много решений доступны, решение с минимальной нормой особенно интересно. Можно использовать lsqminnorm вычислить решение методом наименьших квадратов минимальной нормы. Это решение имеет наименьшее значение для norm(p) .

Решение для нескольких правых сторон

Некоторые проблемы касаются решения линейных систем, которые имеют ту же матрицу коэффициентов A , но различные правые стороны b . Когда различные значения b доступны одновременно, можно создать b как матрица с несколькими столбцами и решают все системы уравнений одновременно с помощью одной команды обратной косой черты: X = A\[b1 b2 b3 …] .

Однако иногда различные значения b не все доступны одновременно, что означает, что необходимо решить несколько систем уравнений последовательно. Когда вы решаете одну из этих систем уравнений с помощью наклонной черты (/) или обратная косая черта (\), оператор разлагает на множители матрицу коэффициентов A и использование это матричное разложение, чтобы вычислить решение. Однако в каждый последующий раз вы решаете аналогичную систему уравнений с различным b , оператор вычисляет то же разложение A , который является избыточным расчетом.

Решение этой проблемы состоит в том, чтобы предварительно вычислить разложение A , и затем снова используйте факторы, чтобы решить для различных значений b . На практике, однако, предварительное вычисление разложения этим способом может затруднить, поскольку необходимо знать, какое разложение вычислить (LU, LDL, Холесский, и так далее), а также как умножить факторы, чтобы решить задачу. Например, с LU-разложением необходимо решить две линейных системы, чтобы решить исходную систему Ax = b:

Вместо этого рекомендуемый метод для решения линейных систем с несколькими последовательными правыми сторонами должен использовать decomposition объекты. Эти объекты позволяют вам усилить выигрыши в производительности предварительного вычисления матричного разложения, но они не требуют знания того, как использовать матричные факторы. Можно заменить предыдущее LU-разложение на:

Если вы не уверены который разложение использовать, decomposition(A) выбирает правильный тип на основе свойств A , похожий на то, что делает обратная косая черта.

Вот простой тест возможных выигрышей в производительности этого подхода. Тест решает ту же разреженную линейную систему 100 раз с помощью и обратной косой черты (\) и decomposition .

Решение СЛАУ и матрицы в Matlab

Доброго времени суток, читатели! Сегодня мы поговорим о матрицах в Matlab, об их применении в решении систем линейных алгебраических уравнений. Подробно разберем методы решения, и для этого необходимо знание нескольких базовых алгоритмов.

Также стоит отметить, что у каждого алгоритма, которым мы будем искать решение СЛАУ в Matlab, своя скорость нахождения этого решения, наличие или отсутствие условия выполнения алгоритма и т.д.

В традициях нашего сайта разберём на примере:

Решить систему линейных уравнений:

4*a + b — c = 6
a — b + c = 4
2*a — 3*b — 3*c = 4

Метод обратной матрицы в Matlab

Начнем с достаточно распространенного метода. Его суть состоит в том, что сначала необходимо выписать коэффициенты при a, b и c (то есть те коэффициенты, которые находятся слева) в одну матрицу, а свободный член (то есть то, что справа) в другую.

В итоге у нас получится 2 матрицы:

Для реализации этого метода (и следующих методов тоже) требуется одно условие: чтобы определитель матрицы, составленной из коэффициентов левой части не был равен нулю. Проверка на определитель:

После проверки условия можем перейти к следующему шагу: нахождение обратной матрицы. В Matlab для этого используется оператор inv .
А само решение СЛАУ в Matlab находится как перемножение найденной обратной матрицы на матрицу свободных членов:

Мы получили 3 значения, которые и соответствуют нашим коэффициентам: то есть a = 2, b = -1, c = 1 . Можете проверить, подставив полученные ответы в исходную систему, и убедиться, что мы решили СЛАУ правильно.

Также следует отметить, что матрицы нужно перемножать именно, как сделали мы, то есть слева обратная матрица, справа матрица свободных членов.

Если вы не все поняли, то советую вам почитать нашу статью по основам Matlab.

Метод Гаусса

Метод Гаусса в Matlab реализуется достаточно просто: для этого нам нужно всего лишь изучить один новый оператор.
(\) — левое деление.
При следующей записи:

Мы получим ответы на нашу исходную систему. Только заметьте, мы решили СЛАУ стандартным набором функций в Matlab, и желательно этот оператор использовать когда матрица коэффициентов квадратная, так как оператор приводит эту матрицу к треугольному виду. В других случаях могут возникнуть ошибки.

Метод разложения матрицы

Теперь поговорим о разложении матрицы. Нахождение решения через разложение матрицы очень эффективно. Эффективность обусловлена скоростью нахождения решения для данного вида систем и точностью полученных результатов.

Возможны следующие разложения:

• разложение Холецкого
• LU разложение
• QR разложение

Разберём решение через LU и QR разложение, так как в задачах чаще всего встречается задание на решение именно через такие разложения.

Основное отличие этих двух разложений: LU разложение применимо только для квадратных матриц, QR — возможно и для прямоугольных.

LU разложение

Решим выше предложенную задачу через LU разложение:

QR разложение

И через QR разложение соответственно:

Отметим, что апостроф ( ‘ ) после Q означает транспонирование.

Стандартные функции Matlab

Так же Matlab предлагает функцию linsolve , с помощью которой возможно решить систему линейных алгебраических уравнений. Выглядит это так:

Как видите, ничего сложного тут нет, на то они и стандартные функции Matlab.

Повторение

Итак, сегодня мы с вами изучили несколько методов для решения СЛАУ в Matlab, как с помощью матриц, так и с помощью стандартных функций. Давайте их повторим на другом примере:

Решить систему линейных уравнений:
6*a — b — c = 0
a — 2*b + 3*d = 0
3*a — 4*b — 4*c = -1

• Методом обратной матрицы:
• Методом Гаусса:
• LU разложение:
• QR разложение:

На этом я с вами попрощаюсь, надеюсь, вы научились применять матрицы в Matlab для решения СЛАУ.

mldivide , \

Solve systems of linear equations Ax = B for x

Syntax

Description

x = A \ B solves the system of linear equations A*x = B . The matrices A and B must have the same number of rows. MATLAB ® displays a warning message if A is badly scaled or nearly singular, but performs the calculation regardless.

If A is a scalar, then A\B is equivalent to A.\B .

If A is a square n -by- n matrix and B is a matrix with n rows, then x = A\B is a solution to the equation A*x = B , if it exists.

If A is a rectangular m -by- n matrix with m

= n , and B is a matrix with m rows, then A \ B returns a least-squares solution to the system of equations A*x= B .

x = mldivide( A , B ) is an alternative way to execute x = A \ B , but is rarely used. It enables operator overloading for classes.

Examples

System of Equations

Solve a simple system of linear equations, A*x = B .

Linear System with Singular Matrix

Solve a linear system of equations A*x = b involving a singular matrix, A .

When rcond is between 0 and eps , MATLAB® issues a nearly singular warning, but proceeds with the calculation. When working with ill-conditioned matrices, an unreliable solution can result even though the residual (b-A*x) is relatively small. In this particular example, the norm of the residual is zero, and an exact solution is obtained, although rcond is small.

When rcond is equal to 0 , the singular warning appears.

In this case, division by zero leads to computations with Inf and/or NaN , making the computed result unreliable.

Least-Squares Solution of Underdetermined System

Solve a system of linear equations, A*x = b .

Linear System with Sparse Matrix

Solve a simple system of linear equations using sparse matrices.

Consider the matrix equation A*x = B .

Input Arguments

A , B — Operands
vectors | full matrices | sparse matrices

Operands, specified as vectors, full matrices, or sparse matrices. A and B must have the same number of rows.

If A or B has an integer data type, the other input must be scalar. Operands with an integer data type cannot be complex.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical | char
Complex Number Support: Yes

Output Arguments

x — Solution
vector | full matrix | sparse matrix

Solution, returned as a vector, full matrix, or sparse matrix. If A is an m -by- n matrix and B is an m -by- p matrix, then x is an n -by- p matrix, including the case when p==1 .

If A has full storage, x is also full. If A is sparse, then x has the same storage as B .

The operators / and \ are related to each other by the equation B/A = (A’\B’)’ .

If A is a square matrix, then A\B is roughly equal to inv(A)*B , but MATLAB processes A\B differently and more robustly.

If the rank of A is less than the number of columns in A , then x = A\B is not necessarily the minimum norm solution. You can compute the minimum norm least-squares solution using x = lsqminnorm (A,B) or x = pinv (A)*B .

Use decomposition objects to efficiently solve a linear system multiple times with different right-hand sides. decomposition objects are well-suited to solving problems that require repeated solutions, since the decomposition of the coefficient matrix does not need to be performed multiple times.

Algorithms

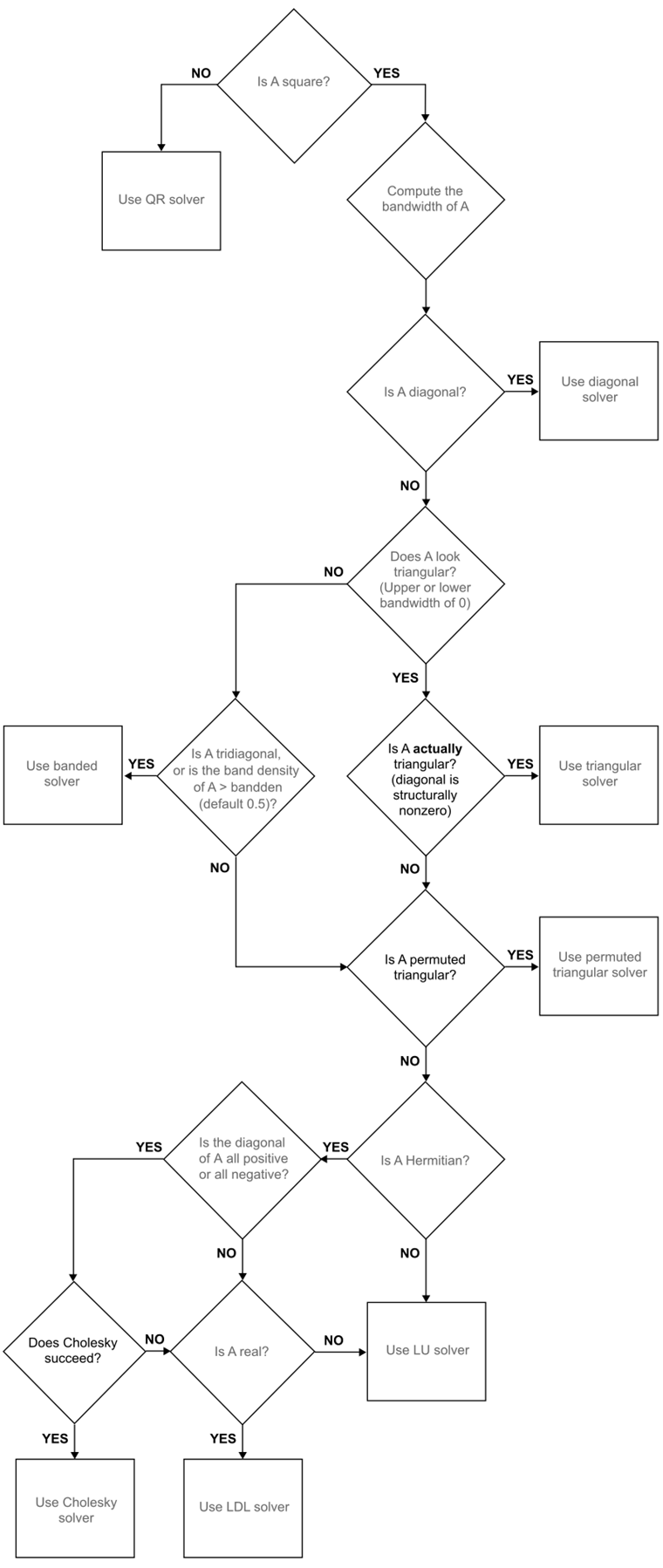
The versatility of mldivide in solving linear systems stems from its ability to take advantage of symmetries in the problem by dispatching to an appropriate solver. This approach aims to minimize computation time. The first distinction the function makes is between full (also called “ dense ”) and sparse input arrays.

Algorithm for Full Inputs

The flow chart below shows the algorithm path when inputs A and B are full.

Algorithm for Sparse Inputs

If A is full and B is sparse then mldivide converts B to a full matrix and uses the full algorithm path (above) to compute a solution with full storage. If A is sparse, the storage of the solution x is the same as that of B and mldivide follows the algorithm path for sparse inputs, shown below.

Extended Capabilities

Tall Arrays
Calculate with arrays that have more rows than fit in memory.

This function supports tall arrays with the limitation:

For the syntax Z = X\Y , the array X must be a scalar or a tall matrix with the same number of rows as Y .

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

For sparse matrix inputs, the language standard must be C99 or later.

GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.

Usage notes and limitations:

For sparse matrix inputs, the language standard must be C99 or later.

Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool .

This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.

GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

Usage notes and limitations:

If A is rectangular, then it must also be nonsparse.

The MATLAB mldivide function prints a warning if A is badly scaled, nearly singular, or rank deficient. The gpuArray mldivide is unable to check for this condition. Take action to avoid this condition.

64-bit integers are not supported.

For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox) .

Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.

Usage notes and limitations:

The MATLAB mldivide function prints a warning if A is badly scaled, nearly singular, or rank deficient. The distributed array mldivide is unable to check for this condition. Take action to avoid this condition.

If A is an M-by-N complex matrix with N > M, for distributed arrays, mldivide computes a solution that minimizes norm(X) . The result is the same as the result of PINV(A)*B .

For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox) .