Систему линейных алгебраических уравнений можно решить используя команду
РЕШЕНИЕ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ
4 Решение уравнений и систем средствами Mathcad
Система Mathcad обладает широкими возможностями численного решения уравнений и систем уравнений.
Функция root, блоки Given…Find, Given…Minerr
В ходе численного решения обычно выделяют два этапа:
- отделение корней – определение интервала нахождения каждого корня или определение приблизительного значения корня. В системе Mathcad наиболее наглядным будет отделение корней уравнения графическим способом;
- уточнение корней – нахождение численного значения корня с указанной точностью.
Точность нахождения корня устанавливается с помощью системной переменной TOL (Convergence Tolerance – Допуск сходимости), которая по умолчанию равна 10 -3 . Чем меньше значение TOL, тем точнее, вообще говоря, находится корень уравнения. Однако оптимальным является TOL = 10 -5 . Переопределить значение TOL можно в окне математических свойств документа Math Options на вкладке Build-In Variables (Встроенные переменные) или присваиванием, например, TOL:=0.0001.
Для решения одного уравнения с одной неизвестной предназначена встроенная функция root, которая в общем виде задается
root(f(x), x, [a, b])
и возвращает значение переменной x, при котором функция f(x) обращается в ноль. Аргументы функции root:
- f(x) – функция левой части уравнения f(x) = 0;
- x – переменная, относительно которой требуется решить уравнение;
- a, b (необязательные) – действительные числа, такие что a -1 слева: A -1 Ax=A -1 b. Учитывая, что A -1 A, вектор-столбец решений системы можно искать в виде
Этот прием используется в Mathcad так:
- задается матрица коэффициентов при неизвестных системы A;
- задается столбец свободных членов b;
- вводится формула для нахождения решения системы X:=A -1 b;
- выводится вектор решений системы X=.
Кроме того, пакет Mathcad имеет встроенную функцию
lsolve(A, b),
возвращающую вектор-столбец решений системы линейных алгебраических уравнений. Аргументами функции lsolve являются матрица коэффициентов при неизвестных системы и столбец свободных членов. Порядок решения аналогичен рассмотренному, но вместо формулы X:=A -1 b используется X:=lsolve(A, b).
Реализовать широко известный метод Гаусса решения систем линейных уравнений позволяет встроенная функция rref(M), возвращающая ступенчатый вид матрицы M. Если в качестве аргумента взять расширенную матрицу системы, то в результате применения rref получится матрица, на диагонали которой – единицы, а последний столбец представляет собой столбец решений системы.
Решение системы линейных уравнений можно осуществить с помощью блоков Given…Find, Given…Minerr. При этом неизвестным системы задается произвольное начальное приближение, а проверка необязательна.
Порядок выполнения лабораторной работы
- Загрузить Mathcad Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad).
- Сохранить в личной папке на диске z:\ новый документ с именем ФИО1, лучше использовать латинские буквы. Производить сохранение регулярно в процессе работы (Ctrl + S).
- Вставить текстовую область Insert / Text Region (Вставка / Область текста) и ввести в поле документа текст:
Лабораторная работа № 4
Решение уравнений и систем в Mathcad.
- В новой текстовой области ввести фамилию, имя, отчество, учебный шифр и номер варианта.
- Выполнить задание 1.
Задание 1. Решить уравнение 
Решение.
Решение данного уравнения будем проводить в два этапа: отделение корней уравнения графически, уточнение корней уравнения.
Определим функцию f(x), равную левой части данного уравнения, когда правая равна нулю:
Зададим ранжированную переменную x на некотором диапазоне с мелким шагом, например:
Вставим в документ графическую область. Для этого выберем дважды пиктограмму с изображением графика 
Снизу по оси абсцисс наберем x, а сбоку по оси ординат введем f(x).
Для появления графика щелкнем левой клавишей мыши вне графической области.
Отформатируем график функции f(x). Для этого щелкнем правой клавишей мыши в области графика и выберем в контекстном меню команду Format (Формат). Установим пересечение осей графика (Crossed – Только оси), добавим вспомогательные линии по координатным осям (Grid Lines – Вспомогательные линии). Отменим при этом автосетку (Autogrid – Автосетка) и установим количество линий сетки, равное 10.
Для подтверждения внесенных изменений нажмем последовательно кнопки Apply (Применить) и ОК.
После указанных преобразований график функции f(x) будет выглядеть следующим образом:
Из графика функции f(x) видно, что уравнение 
Этап отделения корней завершен.
Уточним теперь корни уравнения с помощью функции root.
Присвоим начальное приближение переменной x и укажем точность поиска корня:
Уточним заданное приближение к значению корня с помощью функции root:
Выполним проверку, подтверждающую, что первый корень найден с заявленной точностью:
Начальное приближение можно не задавать при использовании в качестве аргументов root границ отрезка нахождения корня, например, второй корень можно уточнить:
Задание 2. Решить уравнение 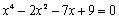
Решение.
Напечатаем левую часть уравнения, не приравнивая выражение к 0, и выделим синим курсором переменную x:
Выберем из главного меню Symbolics / Polynomial Coefficients (Символика / Коэффициенты полинома). Появившийся вектор коэффициентов полинома выделим целиком синим курсором и вырежем в буфер обмена, используя кнопку Вырезать 
Напечатаем v := и вставим вектор из буфера обмена, используя кнопку Вставить 
Для получения результата напечатаем polyroots(v) =:
Задание 3. Решить систему линейных уравнений 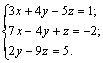
Решение.
1-й способ. Использование блока Given … Find.
Зададим всем неизвестным, входящим в систему уравнений, произвольные начальные приближения, например:
Напечатаем слово Given. Установим визир ниже и наберем уравнения системы, каждое в своем блоке. Используем при этом логический знак равенства (Ctrl + =).
После ввода уравнений системы напечатаем X := Find(x, y, z) и получим решение системы в виде вектора, состоящего из трех элементов:
Сделаем проверку, подставив полученные значения неизвестных в уравнения системы, например, следующим образом
После набора знака «=» в каждой строке должен быть получен результат, равный или приблизительно равный правой части системы. В данном примере системная переменная ORIGIN = 1.
2-й способ. Использование блока Given…Minerr.
Порядок решения системы этим способом аналогичен порядку использования блока Given … Find и представлен ниже вместе с проверкой:
3-й способ. Решение системы линейных уравнений матричным способом.
Создадим матрицу А, состоящую из коэффициентов при неизвестных системы. Для этого напечатаем A := , вызовем окно создания массивов (Ctrl + M). Число строк (Rows) и столбцов (Columns) матрицы данной системы равно 3. Заполним пустые места шаблона матрицы коэффициентами при неизвестных системы, как показано ниже:
Зададим вектор b свободных членов системы. Сначала напечатаем b :=, затем вставим шаблон матрицы(Ctrl + M), где количество строк (Rows) равно 3, а количество столбцов (Columns) равно 1. Заполним его:
Решим систему матричным способом по формуле
Решим систему с помощью функции lsolve:
Для проверки правильности решения системы, полученного матричным способом, достаточно вычислить произведение A·X, которое должно совпасть с вектором-столбцом свободных членов b:
Решение систем линейных алгебраических уравнений. Системы линейных алгебраических уравнений можно решать также, используя команду solve
Системы линейных алгебраических уравнений можно решать также, используя команду solve. Такое решение в силу простоты записи может быть предпочтительным. Для решения система уравнений и перечень неизвестных задаются в виде множеств, то есть с использованием фигурных скобок.
Если для дальнейших вычислений необходимо использовать полученные решения уравнений, то команде solve следует присвоить какое-нибудь имя name. Затем выполняется присвоения команда assign(name). После этого над решениями можно будет производить математические операции.
Решение систем из трех линейных уравнений имеет наглядную геометрическую интерпретацию – в виде точки, в которой пересекаются три плоскости, каждая из которых описывается функцией двух переменных. Это позволяет сделать функция импликативной графики implicitplot3d.
f, expr1 – уравнение поверхности, которая должна быть построена;
a,b,c,d,p,q – пределы изменения соответствующих переменных;
options –параметры, с помощью которых можно в широких пределах управлять видом трехмерных графиков.
С помощью команды solve можно также решить систему неравенств. Например:
ПРАКТИЧЕСКАЯ ЧАСТЬ
Задание 1
Построить графики трех функций sin(x),sin(x)/x, sin(x 3 /100) линиями трех цветов и трех типов.
> plot([sin(x),sin(x)/x, sin(x^3/100)],
x=10..10,color=[black,blue,red],style=[line,line,point]);
Результат представлен на рисунке 5.2.
Рис.5.2 – Графики трех функций
Задание 2
Построить поверхность h 2 в цилиндрической системе координат.
> plot3d(h^2,a=-Pi..Pi,h=-5..5, coords=cylindrical, style=patch, color=sin(h));
Результат представлен на рисунке 5.3
Рис.5.3 – Пример трехмерного графика
Задание 3
Построить поверхности 2*sin(x*y), x^2+y^2-10, -x^2-y^2+10 в одной системе координат
Результат представлен на рисунке 5.4.
Рис.5.4 – Поверхности, построенные в одной системе координат
Задание 4
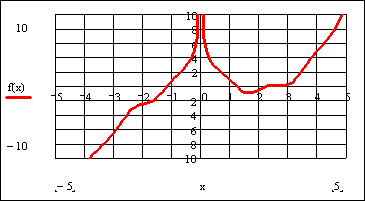
Решить нелинейное уравнение вида y=2x 2 +1.25x-3.2. Выделить графически интервал изоляции корня уравнения и вычислить корень с точностью e = 10 -5 .
Сеанс работы с Maple:
> fn:=2*x^2+1.25*x-3.2; # Определение функции через оператор присваивания
> plot(fn,x=-4..4,y=-5..15);# Графическое выделение интервала изоляции корня
> ans:=evalf(solve(fn,x),5);# Pешение уравнения и присвоение значений корней переменной ans
> x1=ans[1]; # Выделение первого корня уравнения
> x2:=ans[2]; # Выделение второго корня уравнения
> subs(x=ans[1],fn); );# Подстановка первого корня в уравнение
> subs(x=ans[2],fn); );# Подстановка второго корня в уравнение
Задание 5
Решить тригонометрическое уравнение вида y=sin(x 2 )+cos(x 2 ). Выделить графически интервал изоляции корней уравнения на отрезке [-5..5] и вычислить все корни на этом отрезке.
Сеанс работы с Maple:
> fn:=sin(x^2)+cos(x^2); # Определение функции через оператор присваивания
> plot(fn,x=-5..5); # Графическое выделение корней на заданном интервале
> ans:=solve(fn,x); #Pешение уравнения и присвоение значений корней переменной ans
> _EnvAllSolutions:=true;# Получение всех решений
> x1:=ans[1]; # Выделение первого корня уравнения
> x2:=ans[2]; # Выделение второго корня уравнения
> x1*x2; # Действия над корнями
Задание 6
По известным данным о коэффициентах прямых затрат (аij) и конечном продукте(Y)в межотраслевом балансе для трех отраслей (промышленность, строительство, сфера услуг) определить общий выпуск продукции по каждой отрасли (xij). Исходные данные приведены в таблице 5.1.
Таблица 5.1. Исходные данные д ля межотраслевого баланса
| Отрасль-производитель Отрасль-потребитель | Коэффициенты прямых затрат | Конечный продукт, усл. ед. |
| 0,1 | 0,3 | 0,2 |
| 0,2 | 0,2 | 0,3 |
| 0,1 | 0,1 | 0,4 |
Как известно, матричная форма записи межотраслевого баланса имеет вид
где А – матрица коэффициентов прямых затрат;
Y– вектор конечного продукта;
Х – вектор объемов производства.
В натуральном балансе коэффициенты прямых затрат аij означают расход i-той продукции на изготовление единицы j-той продукции.
В стоимостном балансе коэффициенты аij означают затраты i-той отрасли на каждый рубль валовой продукции j-той отрасли.
Помножив вектор Х на единичную матрицу, соотношение (5.1) можно преобразовать как
При известных значениях коэффициентов прямых затрат соотношение (5.3) можно использовать для анализа и планирования и решить следующие задачи:
· определить объемы валовой продукции отраслей X1, X2, …, Xn по заданным объемам конечной продукции по формуле
· определить объемы конечного продукта отраслей Y1, Y2, … , Yn по заданным объемам валовой продукции X1, X2, …, Xn по формуле
На основании вышесказанного по данным таблицы 5.1 можно записать следующую систему уравнений:

X2 = 0.2X1 + 0.2X2 + 0.3X3 + 11
X3 = 0.1X1 + 0.1X2 + 0.47X3 + 8
Превратив конечные продукты отраслей в свободные члены , получим:

X2 — 0.2X1 — 0.2X2 — 0.3X3 = 11
X3 — 0.1X1 — 0.1X2 — 0.4X3 = 8

— 0.2X1 + 0.8X2 — 0.3X3 = 11
— 0.1X1 — 0.1X2 + 0.6X3 = 8
Решение данной системы уравнений осуществляется известными методами линейной алгебры.
Найдем решение этой системы уравнений при помощи функции solve СКМ Maple.
Сеанс работы с Maple:
> ans:=solve(sys,
> subs(ans=
Таким образом, объемы валовой продукции отраслей X1, X2, X3 составят 60, 40 и 30 усл. ед. соответственно.
Задания для самостоятельной работы
Задание 1. Решить нелинейное уравнение (см. таблицу 5.2). Выделить графически интервал изоляции корня уравнения, определить метод решения уравнения и вычислить корень с точностью e = 10 -4 .
| Вариант | Уравнение | Вариант | Уравнение |
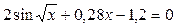 |  | ||
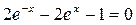 | 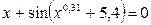 | ||
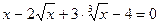 |  | ||
 | 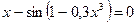 | ||
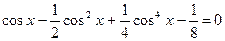 |  | ||
 | 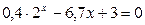 | ||
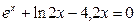 | 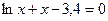 | ||
 | 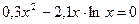 | ||
 |  | ||
 | 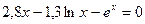 |
Задание 2. Решить неравенство (см. таблицу 5.3).
| Вариант | Неравенство | Вариант | Неравенство |
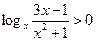 |  | ||
 |  | ||
 |  | ||
 | 9 | 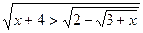 | |
| 5 |  |  |
Задание 3. Решить систему уравнений.
По известным данным о коэффициентах прямых затрат (аij) и конечном продукте (Y) в межотраслевом балансе для трех отраслей (промышленность, строительство, сфера услуг) определить общий выпуск продукции по каждой отрасли (xij).
Предположив, что в прогнозном периоде конечный спрос на продукцию отраслей может измениться (Y1), определить темпы роста промышленного производства.
Вариант 1
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | Изменение конечного спроса Y1, % |
| 0,1 | 0,3 | 0,4 | +20 |
| 0,2 | 0,2 | 0,5 | |
| 0,2 | 0,2 | 0,1 |
Вариант 2
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | Изменение конечного спроса Y1, % |
| 0,2 | 0,2 | 0,1 | |
| 0,5 | 0,3 | 0,2 | +10 |
| 0,2 | 0,1 | 0,4 |
Вариант 3
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | Изменение конечного спроса Y1, % |
| 0,3 | 0,4 | 0,2 | |
| 0,2 | 0,1 | 0,3 | +25 |
| 0,1 | 0,5 | 0,2 |
Вариант 4
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | Изменение конечного спроса Y1, % |
| 0,2 | 0,4 | 0,4 | |
| 0,1 | 0,5 | 0,2 | |
| 0,1 | 0,2 | 0,1 | +10 |
Вариант 5
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | Изменение конечного спроса Y1, % |
| 0,1 | 0,4 | 0,5 | -5 |
| 0,1 | 0,5 | 0,4 | |
| 0,2 | 0,2 | 0,1 |
Вариант 6
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | Изменение конечного спроса Y1, % |
| 0,1 | 0,3 | 0,4 | +10 |
| 0,2 | 0,2 | 0,5 | |
| 0,2 | 0,2 | 0,1 |
Вариант 7
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | Изменение конечного спроса Y1, % |
| 0,3 | 0,1 | 0,1 | |
| 0,4 | 0,3 | 0,5 | +5 |
| 0,5 | 0,2 | 0,1 |
Вариант 8
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | Изменение конечного спроса Y1, % |
| 0,2 | 0,3 | 0,3 | |
| 0,1 | 0,1 | 0,1 | |
| 0,4 | 0,5 | 0,4 | +15 |
Вариант 9
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | Изменение конечного спроса Y1, % |
| 0,1 | 0,5 | 0,4 | |
| 0,2 | 0,2 | 0,1 | -10 |
| 0,2 | 0,4 | 0,4 |
Вариант 10
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | Изменение конечного спроса Y1, % |
| 0,2 | 0,2 | 0,1 | -15 |
| 0,5 | 0,3 | 0,2 | |
| 0,2 | 0,4 | 0,3 |
Задание 4.Решить систему неравенств (см. таблицу 5.4).
| Таблица 5.4.Вариант | Условие | Вариант | Условие |
 |  | ||
 |  | ||
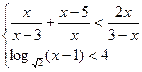 |  | ||
 |  | ||
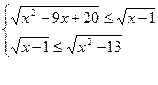 | 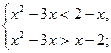 |
Задание 5. Построить поверхность (см. таблицу 5.5):
Методы решения систем линейных алгебраических уравнений (СЛАУ) с примерами
Содержание:
Методы решения систем линейных алгебраических уравнений (СЛАУ)
Метод Крамера
Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение
Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы
Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на 
Второй столбец умножим на 



Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е.
Определение: Определитель 
Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:
31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов.
Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины 
- если главный определитель системы отличен от нуля (
), то система имеет единственное решение;
- если главный определитель системы равен нулю (
), а хотя бы один из вспомогательных определителей отличен от нуля (
или
, или, . или
), то система не имеет решений (деление на нуль запрещено);
- если все определители системы равны нулю (
), то система имеет бесчисленное множество решений.
Пример:
Решить СЛАУ методом Крамера
Решение:
Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом
Найдем главный определитель СЛАУ (раскрываем по первой строке)
Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя
Воспользуемся формулами Крамера
Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений.
Выполним проверку 
Матричный способ решения СЛАУ
Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных 

Тогда СЛАУ можно записать в матричном виде 





Пример:
Решить СЛАУ матричным способом
Решение:
Введем в рассмотрение следующие матрицы
Найдем матрицу 
Пример:
Решение:
Найдем алгебраические дополнения всех элементов 


Отсюда находим, что х = 1; y = l; z = l.
Метод Гаусса
Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции. Расширенная матрица для СЛАУ имеет вид:
Замечание: В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы.
Обменяем в расширенной матрице первую и вторую строки местами, получим 

Умножим элементы первой строки на (—1) и прибавим к соответствующим элементам третьей строки 

Из первого уравнения находим, что х = 1.
Вывод: Из вышеизложенного материала следует, что вне зависимости от
способа решения СЛАУ всегда должен получаться один и тот же ответ.
Замечание: После нахождения решения СЛАУ надо обязательно выполнить проверку, то есть подставить полученные значения неизвестных в заданную СЛАУ и убедиться в тождественности левой части всех равенств системы соответствующим правым частям. Отметим, что задание СЛАУ всегда верно, то есть, если проверка показывает нарушение оговоренной тождественности, то надо искать ошибку в проведенных вычислениях.
Ранг матрицы. Теорема Кронекера-Капелли
Определение: Рангом матрицы 
Если 
При вычислении ранга необходимо начинать вычислять миноры 2 порядка, затем миноры 3 порядка и так далее, пока не будут найдены миноры, обращающиеся в нуль. Если все миноры порядка p равны нулю, то и все миноры, порядок которых больше p, равны нулю.
Пример:
Найти ранг матрицы
Решение:
Очевидно, что среди миноров второго порядка есть миноры отличные от нуля, например, 


Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах.
Следствия из теоремы Кронекера — Капелли
Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).
Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).
В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Экстремум функции
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://lektsii.org/6-64826.html
http://www.evkova.org/metodyi-resheniya-sistem-linejnyih-algebraicheskih-uravnenij-slau

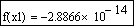
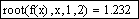
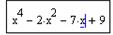
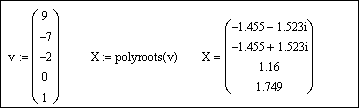
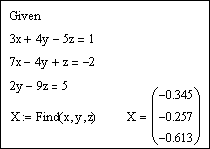
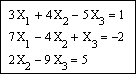


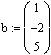
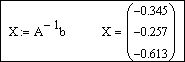
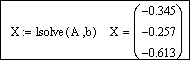






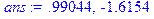


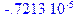

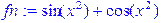





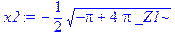


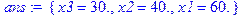
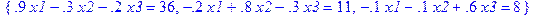







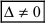 ), то система имеет единственное решение;
), то система имеет единственное решение;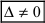 ), а хотя бы один из вспомогательных определителей отличен от нуля (
), а хотя бы один из вспомогательных определителей отличен от нуля ( 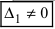 или
или 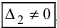 , или, . или
, или, . или 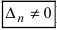 ), то система не имеет решений (деление на нуль запрещено);
), то система не имеет решений (деление на нуль запрещено);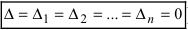 ), то система имеет бесчисленное множество решений.
), то система имеет бесчисленное множество решений.












