Системы дифференциальных уравнений первого порядка с постоянными коэффициентами

Системы дифференциальных уравнений 1-го порядка

Оглавление

Системы обыкновенных дифференциальных уравнений. 1

2. Системы дифференциальных уравнений 1-го порядка. 3

3. Системы линейных дифференциальных уравнений 1-го порядка. 2

4. Системы линейных однородных дифференциальных уравнений с постоянными коэффициентами. 3

5. Системы неоднородных дифференциальных уравнений 1-го порядка с постоянными коэффициентами. 2

Преобразование Лапласа. 1

7. Свойства преобразования Лапласа. 3

8. Приложения преобразования Лапласа. 2

Введение в интегральные уравнения. 1

10. Элементы общей теории линейных интегральных уравнений. 3

11. Понятие об итерационном решении интегральных уравнений Фредгольма 2-го рода. 2

12. Уравнение Вольтерра. 2

13. Решение уравнений Вольтерра с разностным ядром с использованием преобразования Лапласа. 2

Системы обыкновенных дифференциальных уравнений

Введение

Системы обыкновенных дифференциальных уравнений состоят из нескольких уравнений, содержащих производные неизвестных функций одного переменного. В общем случае такая система имеет вид

где – неизвестные функции, t – независимая переменная, – некоторые заданные функции, индекс нумерует уравнения в системе. Решить такую систему – значит найти все функции , удовлетворяющие этой системе.

В качестве примера рассмотрим уравнение Ньютона, описывающее движение тела массы под действием силы :

где – вектор, проведенный из начала координат к текущему положению тела. В декартовой системе координат его компонентами являются функции Таким образом, уравнение (1.2) сводится к трем дифференциальным уравнениям второго порядка

Для нахождения функций в каждый момент времени , очевидно, надо знать начальное положение тела и его скорость в начальный момент времени – всего 6 начальных условий (что отвечает системе из трёх уравнений второго порядка):

Уравнения (1.3) вместе с начальными условиями (1.4) образуют задачу Коши, которая, как ясно из физических соображений, имеет единственное решение, дающее конкретную траекторию движения тела, если сила удовлетворяет разумным критериям гладкости.

Важно отметить, что эта задача может быть сведена к системе из 6 уравнений первого порядка введением новых функций. Обозначим функции как , и введем три новые функции , определенные следующим образом

Систему (1.3) теперь можно переписать в виде

Таким образом, мы пришли к системе из шести дифференциальных уравнений первого порядка для функций Начальные условия для этой системы имеют вид

Первые три начальных условия дают начальные координаты тела, последние три – проекции начальной скорости на оси координат.

Пример 1.1. Свести систему двух дифференциальных уравнений 2-го порядка

к системе из четырех уравнений 1-го порядка.

Решение. Введем следующие обозначения:

При этом исходная система примет вид

Еще два уравнения дают введенные обозначения:

Окончательно, составим систему дифференциальных уравнений 1-го порядка, эквивалентную исходной системе уравнений 2-го порядка

Эти примеры иллюстрируют общую ситуацию: любая система дифференциальных уравнений может быть сведена к системе уравнений 1-го порядка. Таким образом, в дальнейшем мы можем ограничиться изучением систем дифференциальных уравнений 1-го порядка.

Системы дифференциальных уравнений 1-го порядка

В общем виде систему из n дифференциальных уравнений 1-го порядка можно записать следующим образом:

где – неизвестные функции независимой переменной t, – некоторые заданные функции. Общее решение системы (2.1) содержит n произвольных констант, т.е. имеет вид:

При описании реальных задач с помощью систем дифференциальных уравнений конкретное решение, или частное решение системы находится из общего решения заданием некоторых начальных условий. Начальное условие записывается для каждой функции и для системы n уравнений 1-го порядка выглядит так:

Решения определяют в пространстве линию, которая называется интегральной линией системы (2.1).

Сформулируем теорему существования и единственности решения для систем дифференциальных уравнений.

Теорема Коши. Система дифференциальных уравнений 1-го порядка (2.1) вместе с начальными условиями (2.2) имеет единственное решение (т.е. из общего решения определяется единственный набор констант ), если функции и их частные производные по всем аргументам ограничены в окрестности этих начальных условий.

Естественно речь идет о решении в какой-то области переменных .

Решение системы дифференциальных уравнений можно рассматривать как вектор-функцию X, компонентами которого являются функции а набор функций – как вектор-функцию F, т.е.

Используя такие обозначения, можно кратко переписать исходную систему (2.1) и начальные условия (2.2) в так называемой векторной форме:

(2.1a)

(2.2a)

Одним из методов решения системы дифференциальных уравнений является сведение этой системы к одному уравнению более высокого порядка. Из уравнений (2.1), а также уравнений, полученных их дифференцированием, можно получить одно уравнение n-го порядка для любой из неизвестных функций Интегрируя его, находят неизвестную функцию Остальные неизвестные функции получаются из уравнений исходной системы и промежуточных уравнений, полученных при дифференцировании исходных.

Пример 2.1. Решить систему двух дифференциальных первого порядка

сведя его к одному уравнению 2-го порядка.

Решение. Продифференцируем второе уравнение:

Производную выразим через первое уравнение

Из второго уравнения

Мы получили линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами. Его характеристическое уравнение

откуда получаем Тогда общим решением данного дифференциального уравнения будет

Мы нашли одну из неизвестных функций исходной системы уравнений. Пользуясь выражением можно найти и :

Решим задачу Коши при начальных условиях

Подставим их в общее решение системы

и найдем константы интегрирования:

Таким образом, решением задачи Коши будут функции

Графики этих функций изображены на рисунке 1.

Рис. 1. Частное решение системы примера 2.1 на интервале

Пример 2.2.Решить систему

сведя его к одному уравнению 2-го порядка.

Решение. Дифференцируя первое уравнение, получим

Пользуясь вторым уравнением, приходим к уравнению второго порядка для x:

Нетрудно получить его решение, а затем и функцию , подставив найденное в уравнение . В результате имеем следующее решение системы:

Замечание. Мы нашли функцию из уравнения . При этом на первый взгляд кажется, что можно получить то же самое решение, подставив известное во второе уравнение исходной системы

и проинтегрировав его. Если находить таким образом, то в решении появляется третья, лишняя константа:

Однако, как нетрудно проверить, исходной системе функция удовлетворяет не при произвольном значении , а только при Таким образом, определять вторую функцию следует без интегрирования.

Сложим квадраты функций и :

Полученное уравнение дает семейство концентрических окружностей с центром в начале координат в плоскости (см. рисунок 2). Полученные параметрические кривые называются фазовыми кривыми, а плоскость, в которой они расположены – фазовой плоскостью.

Подставляя какие-либо начальные условия в исходное уравнение, можно получить определенные значения констант интегрирования , а значит окружность с определенным радиусом в фазовой плоскости. Таким образом, каждому набору начальных условий соответствует конкретная фазовая кривая. Возьмем, например, начальные условия . Их подстановка в общее решение дает значения констант , таким образом, частное решение имеет вид . При изменении параметра на интервале мы следуем вдоль фазовой кривой по часовой стрелке: значению отвечает точка начального условия на оси , значению — точка на оси , значению — точка на оси , значению — точка на оси , при мы возвращаемся в начальную точку .

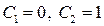
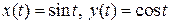
Рис. 2. Фазовая плоскость для примера 2.2

Иногда систему дифференциальных уравнений удается легко решить, подобрав интегрируемые комбинации неизвестных функций. Рассмотрим этот метод решения на примере.

Пример 2.3. Решить систему

подобрав интегрируемую комбинацию.

Решение. Складывая эти два уравнения, получим

Разделяя переменные, решаем это дифференциальное уравнение относительно :

или

Вычтем из первого уравнения второе и решим полученное дифференциальное уравнение относительно :

Из двух полученных уравнений теперь нетрудно выразить и :

(множитель 1/2 был внесен в константы интегрирования).

Задачи

Решить следующие системы дифференциальных уравнений повышением порядка и решить задачу Коши с произвольными начальными условиями.

2.1 2.6

2.2 2.7

2.3 2.8

2.4 2.9

2.5 2.10

Ответы

2.1 2.6

2.2 2.7

2.3 2.8

2.4 2.9

2.5 2.10

Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)

Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

Линейные системы дифференциальных уравнений с постоянными коэффициентами

Линейные системы дифференциальных уравнений с постоянными коэффициентами

1. Общий вид линейной системы дифференциальных уравнений. Однородные и неоднородные системы. Случаи системы с постоянными коэффициентами

2. Основные свойства линейной системы дифференциальных уравнений

3. Основные способы решения однородной линейной системы

4. Понятие о фундаментальной системе решений однородной линейной системы

5. Построение общего решения однородной линейной системы по фундаментальной системе решений

6. Построение фундаментальной системы решения однородной системы с постоянными коэффициентами методом Эйлера

7. Структура общего решения неоднородной линейной системы

1. Общий вид линейной системы дифференциальных уравнений. Однородные и неоднородные системы. Случаи системы с постоянными коэффициентами

Для решения многих задач математики, физики, техники (задач динамики криволинейного движения; задач электротехники движения; задач электротехники для нескольких электрических цепей; определения состава системы, в которой протекают несколько последовательных химических реакций I порядка; отыскания векторных линий поля и других) нередко требуется несколько функций. Нахождение этих функций может привести к нескольким дифференциальным уравнении ям (ДУ), образующим систему.

Системой ДУ называется совокупность ДУ, каждое из которых содержит независимую переменную, искомые функции и их производные.

Нормальной системой линейных ДУ с действительными коэффициентами, называется система вида:

или более коротко

(2)

где — действительная матрица, а — действительный вектор, определенный при .

Однородной системой линейных уравнений, соответствующей системе (2), называется система уравнений

(3)

Система линейных дифференциальных уравнений с постоянными коэффициентами имеет вид

, (1.1)

где — -мерный вектор, — постоянная квадратная матрица размера .

2. Основные свойства линейной системы дифференциальных уравнений

Теорема 1. Линейная комбинация решений однородной системы (3) также является решением этой системы.

Теорема 2. Разность любых двух решений неоднородной системы уравнений (2) есть решение однородной системы (3).

Сумма любого частного решения неоднородной системы (2) и решения соответствующей однородной системы (3) есть решение неоднородной системы (2).

Теорема 3. Если и — решения систем уравнений

— решение системы уравнений

.

Теорема 4. Пусть () – решение системы уравнений (2), матрица и вектор непрерывны на отрезке . Пусть (где означает норму матрицы : ) и . Тогда для имеет место следующая оценка:

(4)

В частности, для линейной однородной системы (3) имеем оценку ():

(5)

Теорема 5. Пусть матрица системы (2) непрерывна на отрезке и . Тогда решение системы (2) однозначно определяется на отрезке условием

. (6)

Итак, из оценки (5) вытекает единственность решения задачи Коши для линейной системы (2) с непрерывной матрицей .

Следствие 1. Пусть матрица непрерывна на отрезке , тогда и для решения однородной системы (3) имеет место оценка

(7)

Иначе говоря, рост функции ограничен экспонентой.

Следствие 2. Решение однородной линейной системы с непрерывной матрицей тождественно равно нулю, если оно равно нулю в какой либо точке отрезка .

3. Основные способы решения однородной линейной системы

Линейные системы можно интегрировать различными способами, например методом исключения, путем нахождения интегрируемых комбинаций и т. д.

Для интегрирования однородных линейных систем с постоянными коэффициентами применяется метод Эйлера, который будет рассмотрен ниже.

4. Понятие о фундаментальной системе решений однородной линейной системы

Определение 1. Решения однородной системы (3) называются линейно независимыми на отрезке , если в каждой точке векторы линейно независимы.

Пусть задана система решений однородной системы (3), определенных на :

() (8)

Определение 2. Определитель

(9)

называется определителем Вронского системы решений .

Определение 3. Система из решений однородной системы уравнений (3), линейно независимых на отрезке называется фундаментальной.

5. Построение общего решения однородной линейной системы по фундаментальной системе решений

Определение 4. Общим решением линейной системы уравнений (2) называется множество всех решений этой системы.

Теорема 8. Пусть — фундаментальная система решений однородной системы уравнений (3), тогда формула

(15) где — произвольные постоянные, дает общее решение этой системы. Множество всех решений однородной системы уравнений (3) образует -мерное векторное пространство, базисом которого может служить любая фундаментальная система решений.

6. Построение фундаментальной системы решения однородной системы с постоянными коэффициентами методом Эйлера

Система линейных дифференциальных уравнений с постоянными коэффициентами имеет вид

, (1.1)

где — -мерный вектор, — постоянная квадратная матрица размера .

Метод Эйлера заключается в следующем. Решение системы (1.1) ищем в виде

,. (2.1)

Функция (2.1) является решением системы (1.1), если — собственное значение матрицы , а — собственный вектор этой матрицы, соответствующий числу . Если собственные значения матрицы попарно различны и — соответствующие собственные векторы этой матрицы, то общее решение системы уравнений (1.1) определяется формулой

,

где — произвольные числа. Если для кратного собственного значения матрицы имеется столько линейно независимых собственных векторов , какова его кратность, то ему соответствуют линейно независимых решений исходной системы: .

Если для собственного значения кратности имеется только линейно независимых собственных векторов, то решения, соответствующие , можно искать в виде произведения векторного многочлена степени на , т. е. в виде

.

Чтобы найти векторы , надо подставить выражение (2.1) в систему (1). Приравняв коэффициенты в левой и правой частях системы, получим уравнения для нахождения векторов .

Если среди собственных чисел матрицы имеются комплексные числа, то указанным выше методом строится соответствующее такому собственному числу решение системы (1.1) через комплексные функции. Чтобы выразить решение через действительные функции (в случае действительной матрицы ), надо воспользоваться тем, что вещественная и мнимая части комплексного решения, соответствующего собственному числу (), являются линейно независимыми решениями.

7. Структура общего решения неоднородной линейной системы,

Пусть — частное решение неоднородное решение неоднородной системы уравнений (2), а — фундаментальная система решений однородной системы уравнений (3). Тогда формула

, (16)

где — произвольные постоянные, дает общее решение неоднородной системы уравнений (2).

Теорема 9. Пусть на отрезке матрица и вектор непрерывны, и пусть известна фундаментальная система решений для однородной системы уравнений (3). Тогда общее решение неоднородной системы уравнений (2) находится с помощью квадратур.

Доказательство. Пусть — фундаментальная система решений для уравнения (3), тогда

()

или в матричной форме

, (17)

где — матрица, называемая фундаментальной матрицей системы уравнений (3). Определитель фундаментальной матрицы есть определитель Вронского и поэтому отличен от нуля на отрезке : .

Будем искать решение системы уравнений (2) в виде

, (18) где .

Подставляя выражение (18) в (2), получим

. (19)

В силу (17) уравнение (19) примет вид

(20) Так как и матрица непрерывна на , то существует непрерывная на обратная матрица .

Умножая обе части уравнения (20) слева на , получим

,

( 21)

где — произвольный постоянный вектор. Подставляя найденное выражение (21) для в формулу (18), получим

(22) Формула (22) дает общее решение неоднородной системы уравнений (2). Решение задачи Коши для системы (2) задается формулой

.

Метод нахождения решения системы (2) называется методом вариации постоянных или методом неопределенных коэффициентов Лагранжа.

Практически удобно поступать следующим образом: Уравнение (20) в развернутом виде

представляет собой систему линейных уравнений относительно :

,

,

.

Решая эту систему относительно (), получим или

.

Подставляя найденные выражения для в (18) получим общее решение для системы (2).

1. , Рождественский дифференциальные уравнения и основы вариационного исчисления. – М.: Наука, с.

2. и др. Сборник задач по обыкновенным дифференциальным уравнениям: Учеб. пособие для втузов. – М.: Высш. шк., с.: ил.

3. , , Перестюк уравнения: примеры и задачи: Учеб. пособие. – М.: Высш. шк., с.: ил.