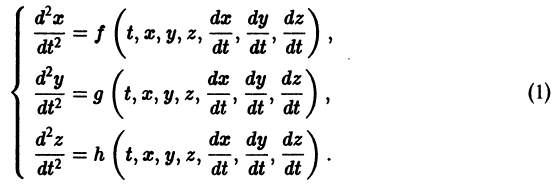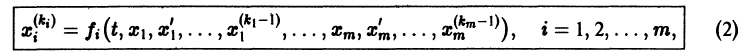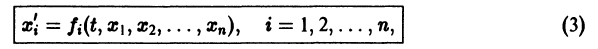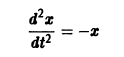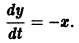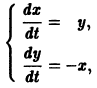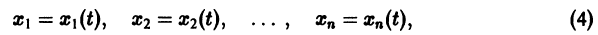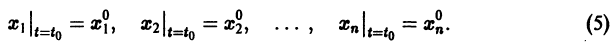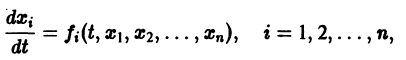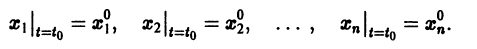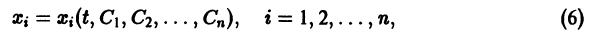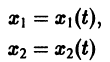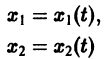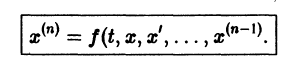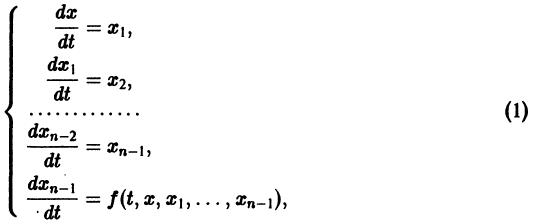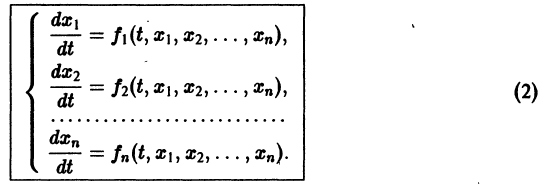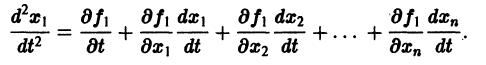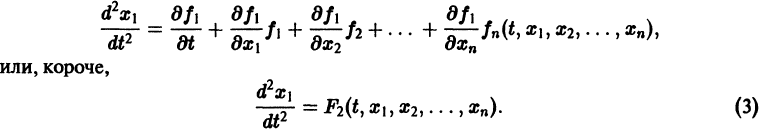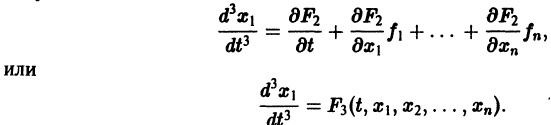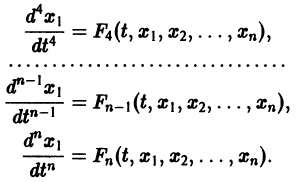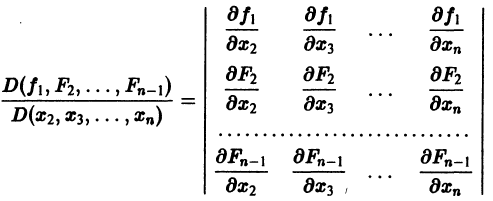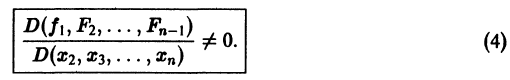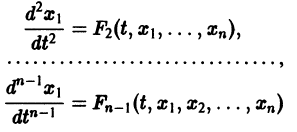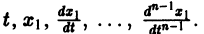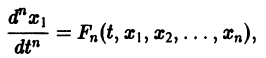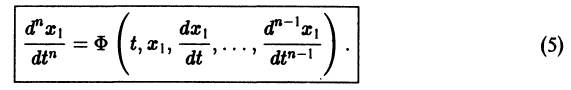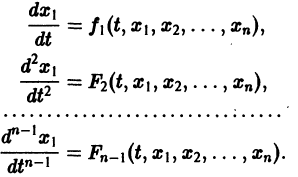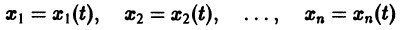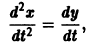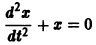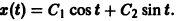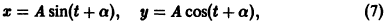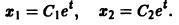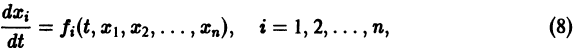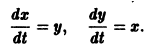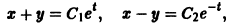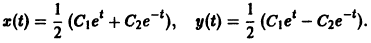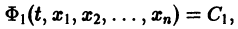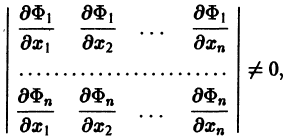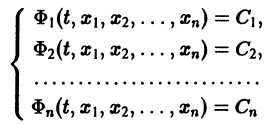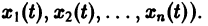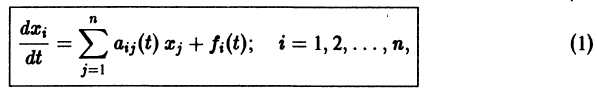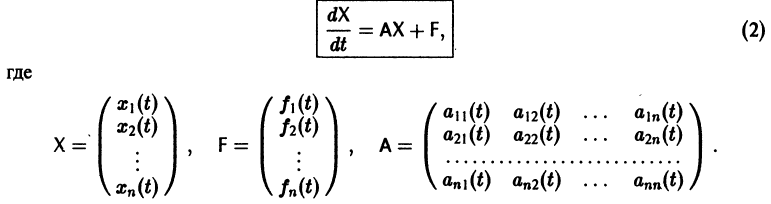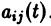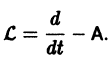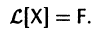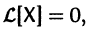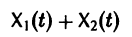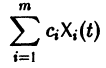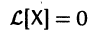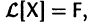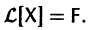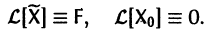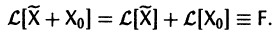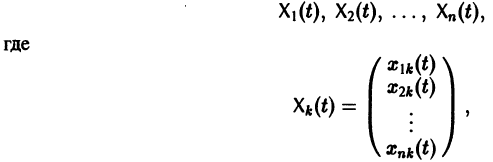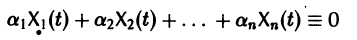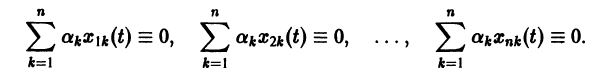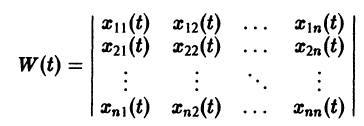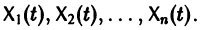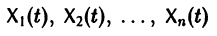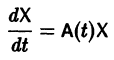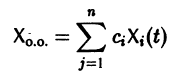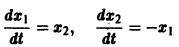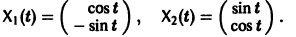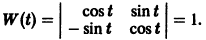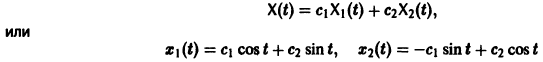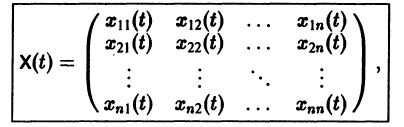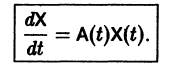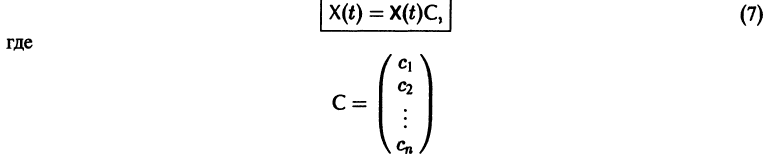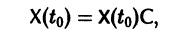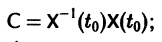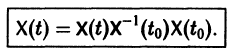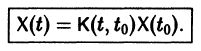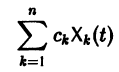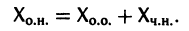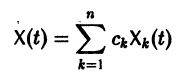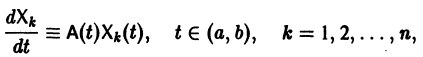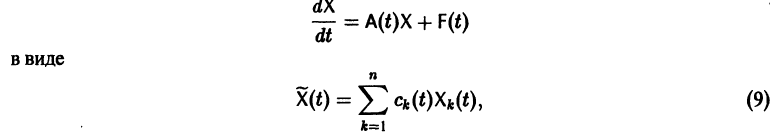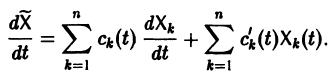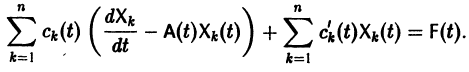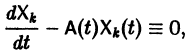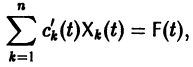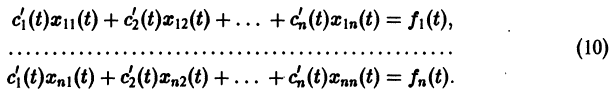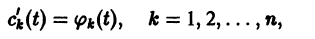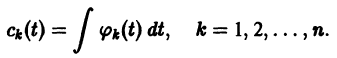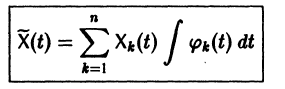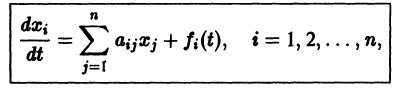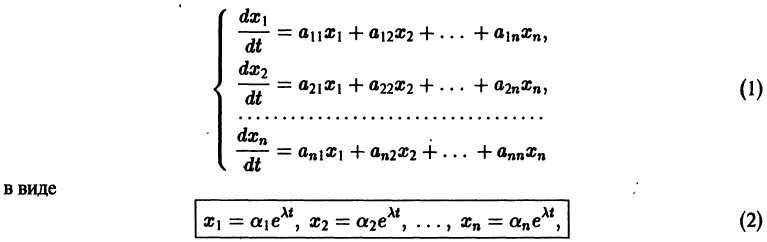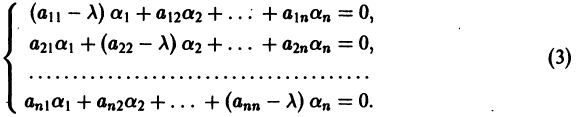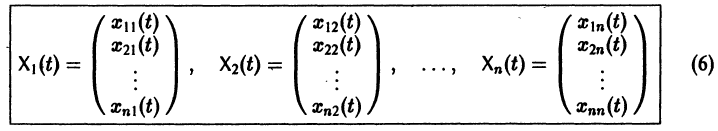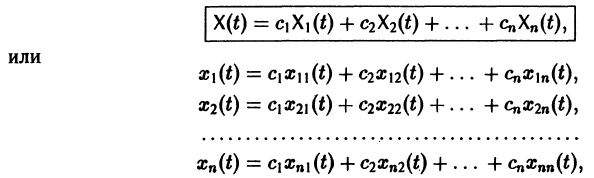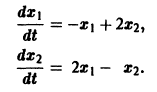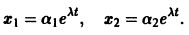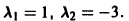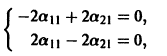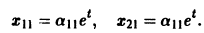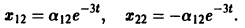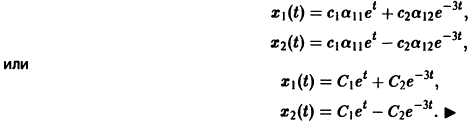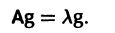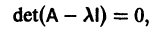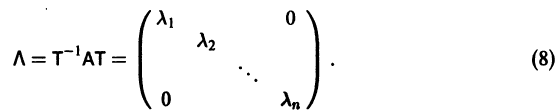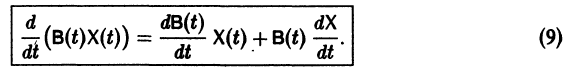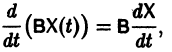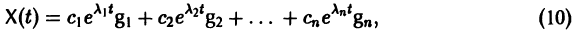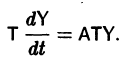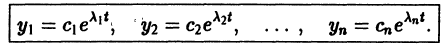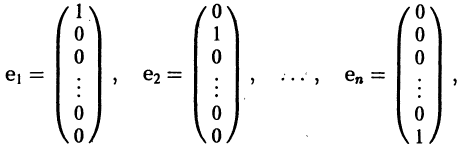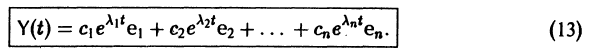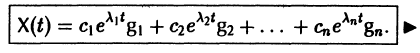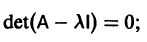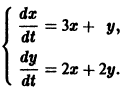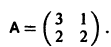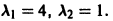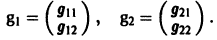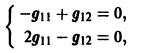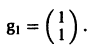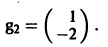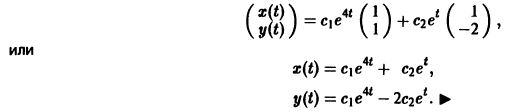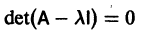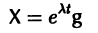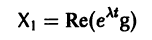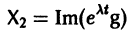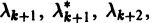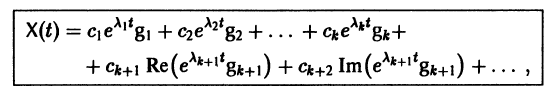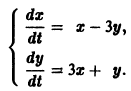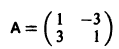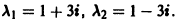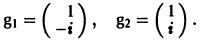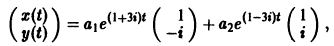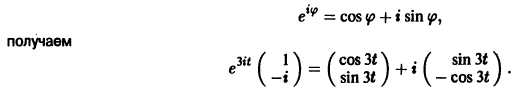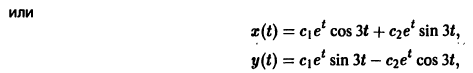Системы дифференциальных уравнений с параметром

Параметрическая идентификация линейной динамической системы

Введение

Немного из теории

Для начала нужно понять, что такое динамическая система. Если говорить как можно проще, то это система, параметры которой изменяются во времени. Подробнее здесь. Практически любую динамическую систему можно описать дифференциальным уравнением какого-либо порядка, например:

Данная система дифференциальных уравнений характеризуется своими параметрами. В нашем случае это a, b, c и d. Они могут быть как статическими так и динамическими .

Так вот задача параметрической идентификации это определение этих самых коэффициентов параметров a, b, c и d.

Задача наблюдения и измерения

Стоит отметить, что для решения задачи параметрической идентификации необходимо получить «измерения» одной (или всех) фазовой координаты (в нашем случае это x₁ и (или) x₂).

Для того чтобы система была идентифицируема, она должна быть наблюдаема. То есть ранг матрицы наблюдаемости должен быть равен порядку системы. Подробнее про наблюдаемость здесь.

Наблюдение процессов, происходящих в объекте, происходит следующим образом:

где:

• у — вектор наблюдаемых параметров;
• H — матрица связи параметров состояния и наблюдаемых параметров;

— помеховая составляющая (в ней спрятаны все погрешности наблюдения);

Измерение процессов, происходящих в объекте, описывается следующим образом:

Как мы видим погрешность измерения может быть как аддитивной (в первом случае), так и мультипликативной(во втором)

Задача идентификации

Рассмотрим решение задачи параметрической идентификации в случае когда не известен один коэффициент. Перейдем к конкретному примеру. Пусть дана следующая система:

Видно, что параметры равны b = 1, c = 0.0225 и d = -0.3. Параметр a нам неизвестен. Попробуем дать его оценку с помощью метода наименьших квадратов.

Задача состоит в следующем: по имеющимся выборочным данным наблюдений за выходным сигналами с интервалом дискретизации Δt требуется оценить значения параметра, обеспечивающего минимум величины функционала невязки между модельными и фактическими данными.

где — невязка, определённая как разность между выходом исследуемого объекта и реакцией, вычисленной по математической модели объекта.

Невязка складывается из неточностей структуры модели, погрешностей измерений и неучтённых взаимодействий среды и объекта. Однако, независимо от природы возникающих ошибок, метод наименьших квадратов минимизирует сумму квадратичной невязки для дискретных значений. В принципе, МНК не требует никакой априорной информации о помехе. Но для того, чтобы полученные оценки обладали желательными свойствами, будем предполагать, что помеха является случайным процессом типа белого шума.

Оценка по методу наименьших квадратов, минимизирующая критерий J, находится из условия существования минимума функционала:

Важным свойством оценок по МНК является существование только одного локального минимума, совпадающего с глобальным. Поэтому оценка является единственной. Ее значение определяется из условия экстремума функционала J:

То есть необходимо от функционала взять производную по a и приравнять ее к нулю.

Обращаю внимание, что — это «измеренные» значения фазовых координат и (или) , а — это фазовые координаты и (или) вычисленные по математической модели объекта. Но ведь в модели объекта, представленной в виде системы дифференциальных уравнений, и не выражены в явном виде. Для того, чтобы избавиться от этого безумия необходимо решить данную систему дифференциальных уравнений с заданными начальными условиями.

Решать можно как «вручную», так и используя какое-либо программное обеспечение. Ниже будет показано решение в MatLab. В итоге должна получится система алгебраических уравнений для каждого момента времени :

Затем подставляя вместо значения «измеренных» фазовых координат, находим оценку параметра для каждого момента времени .

Где взять эти «измеренные» значения фазовых координат?

Вообще эти значения берутся из эксперимента. Но так как мы никакой эксперимент не проводили, то возьмем эти значения из численного решения нашей системы дифференциальных уравнений методом Рунге-Кутта 4-5 порядка. Выберем параметр

Решение найдем встроенными функциями пакета MatLab. Подробнее здесь. Решение данным методом показано ниже.

Ниже показан код на MatLab и график.

На графике синей пунктирной линией обозначена оценка параметра , а красной сплошной линией обозначено непосредственно «истинное» значение параметра модели . Мы видим, что примерно на 3,5 секунде процесс стабилизируется. Небольшое расхождение оценки параметра и «истинного» значения вызвано ошибками при решении системы дифференциальных уравнений методом Рунге-Кутта.

Системы дифференциальных уравнений с примерами решения и образцами выполнения

Также как и обыкновенные дифференциальные уравнения, системы дифференциальных уравнений применяются для описания многих процессов реальной действительности. В частности, к ним относятся различного рода физические и химические процессы, процессы нефте- и газодобычи, геологии, экономики и т.д. Действительно, если некоторые физические величины (перемещение тела, пластовое давление жидкости в фиксированной точке с тремя координатами, концентрация веществ, объемы продаж продуктов) оказываются меняющимися со временем под воздействием тех или иных факторов, то, как правило, закон их изменения по времени описывается именно системой дифференциальных уравнений, т.е. системой, связывающей исходные переменные как функции времени и производные этих функций. Независимой переменной в системе дифференциальных уравнений может выступать не только время, но и другие физические величины: координата, цена продукта и т.д.

Решение систем дифференциальных уравнений

К системе дифференциальных уравнений приводит уже простейшая задача динамики точки: даны силы, действующие на материальную точку; найти закон движения, т. е. найти функции 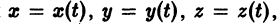выражающие зависимость координат движущейся точки от времени. Система, которая при этом получается, в общем случае имеет вид

Здесь x, у, z — координаты движущейся точки, t — время, f, g, h — известные функции своих аргументов.

Система вида (1) называется канонической. Обращаясь к общему случаю системы т дифференциальных уравнений с т неизвестными функциями 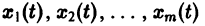аргумента t, назовем канонической систему вида

разрешенную относительно старших производных. Система уравнений первого порядка, разрешенных относительно производных от искомых функций,

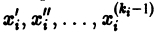
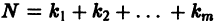
Если в (2) принять за новые вспомогательные функции, то общую каноническую систему (2) можно заменить эквивалентной ей нормальной системой, состоящей из уравнений. Поэтому достаточно рассматривать лишь нормальные системы.

Например, одно уравнение

является мастным случаем канонической системы. Положив 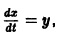в силу исходного уравнения будем иметь

В результате получаем нормальную систему уравнений

эквивалентную исходному уравнению.

Определение:

Решением нормальной системы (3) на интервале (а, Ь) изменения аргумента t называется всякая система n функций

дифференцируемых на интервале а

Теорема:

Существования и единственности решения задачи Коши. Пусть имеем нормальную систему дифференциальных уравнений

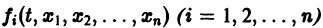
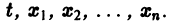
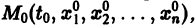
и пусть функции определены в некоторой (n + 1) — мерной области D изменения переменных Если существует окрестность точки в которой функции fi непрерывны по совокупности аргументов и имеют ограниченные частные производные по переменным то найдется интервал изменения t, на котором существует единственное решение нормальной системы (3), удовлетворяющее начальным условиям

Определение:

Система n функций

зависящих от t и n произвольных постоянных называется общим решением нормальной системы (3) в некоторой области существования и единственности решения задачи Коши, если

1) при любых допустимых значениях система функций (6) обращает уравнения (3) в тождества,

2) в области функции (6) решают любую задачу Коши.

Решения, получающиеся из общего при конкретных значениях постоянных называются частными решениями.

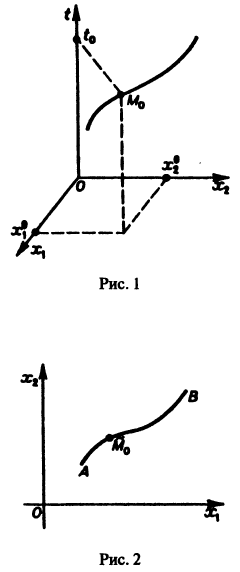
Обратимся для наглядности к нормальной системе двух уравнений,

Будем рассматривать систему значений t, x1, х2 как прямоугольные декартовы координаты точки трехмерного пространства, отнесенного к системе координат 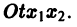Решение

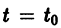
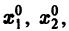
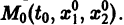
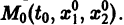
системы (7), принимающее при значения определяет в пространстве некоторую линию, проходящую через точку Эта линия называется интегральной кривой нормальной системы (7). Задача Коши для системы (7) получает следующую геометрическую формулировку: в пространстве переменных t, x1, х2 найти интегральную кривую, проходящую через данную точку (рис. 1). Теорема 1 устанавливает существование и единственность такой кривой.

Нормальной системе (7) и ее решению можно придать еще такое истолкование: будем независимую переменную t рассматривать как параметр, а решение

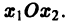
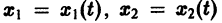
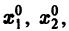
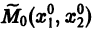
системы — как параметрические уравнения кривой на плоскости Эту плоскость переменных х1х2 называют фазовой плоскостью. В фазовой плоскости решение системы (7), принимающее при t = to начальные значения изображается кривой АВ, проходящей через точку (рис. 2). Эту кривую называют траекторией системы (фазовой траекторией). Траектория системы (7) есть проекция интегральной кривой на фазовую плоскость. По интегральной кривой фазовая траектория определяется однозначно, но не наоборот.

Методы интегрирования систем дифференциальных уравнений

Метод исключения

Один из методов интегрирования — метод исключения. Частным случаем канонической системы является одно уравнение n-го порядка, разрешенное относительно старшей производной

Введя новые функции 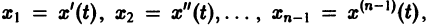заменим это уравнение следующей нормальной системой n уравнений:

т. е. одно уравнение n-го порядка эквивалентно нормальной системе (1)

Можно утверждать и обратное, что, вообще говоря, нормальная система п уравнений первого порядка эквивалентна одному уравнению порядка n. На этом и основан метод исключения для интегрирования систем дифференциальных уравнений.

Делается это так. Пусть имеем нормальную систему

Продифференцируем первое из уравнений (2) по t. Имеем

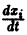
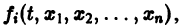
Заменяя в правой части производные их выражениями получим

Уравнение (3) снова дифференцируем по t. Принимая во внимание систему (2), получим

Продолжая этот процесс, найдем

Предположим, что определитель

(якобиан системы функций отличен от нуля при рассматриваемых значениях

Тогда система уравнений, составленная из первого уравнения системы (2) и уравнений

будет разрешима относительно неизвестных При этом выразятся через

Внося найденные выражения в уравнение

получим одно уравнение n-го порядка

Из самого способа его построения следует, что если 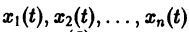есть решения системы (2), то функция х1(t) будет решением уравнения (5).

Обратно, пусть Х1(t) — решение уравнения (5). Дифференцируя это решение по t, вычислим 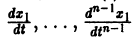и подставим найденные значения как известные функции

от t в систему уравнений

По предположению эту систему можно разрешить относительно т. е найти как функции от t.

Можно показать, что так построенная система функций

составляет решение системы дифференциальных уравнений (2). Пример:

Требуется проинтегрировать систему

Дифференцируя первое уравнение системы, имеем

откуда, используя второе уравнение, получаем

— линейное дифференциальное уравнение второго порядка с постоянными коэффициентами с одной неизвестной функцией. Его общее решение имеет вид

В силу первого уравнения системы находим функцию

Найденные функции x(t), y(t), как легко проверить, при любых значениях С1 и С2 удовлетворяют заданной системе.

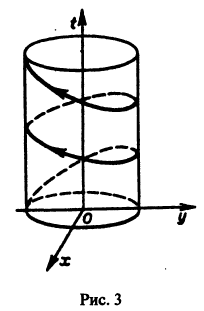
Функции x(t), y(t) можно представить в виде

откуда видно, что интегральные кривые системы (6) — винтовые линии с шагом 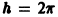и с общей осью х = у = 0, которая также является интегральной кривой (рис. 3).

Исключая в формулах (7) параметр t, получаем уравнение

так что фазовые траектории данной системы суть окружности с центром в начале координат — проекции винтовых линий на плоскость хОу.

При А = 0 фазовая траектория состоит из одной точки х = 0, у = 0, называемой точкой покоя системы.

Замечание:

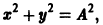
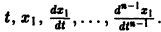
Может оказаться, что функции нельзя выразить через Тогда уравнения n-го порядка, эквивалентного исходной системе, мы не получим. Вот простой пример. Систему уравнений

нельзя заменить эквивалентным уравнением второго порядка относительно х1 или x2. Эта система составлена из пары уравнений 1-го порядка, каждое из которых интегрируется независимо, что дает

Метод интегрируемых комбинаций

Интегрирование нормальных систем дифференциальных уравнений

иногда осуществляется методом интегрируемых комбинаций.

Интегрируемой комбинацией называется дифференциальное уравнение, являющееся следствием уравнений (8), но уже легко интегрирующееся.

Пример:

Складывая почленно данные уравнения, находим одну интегрируемую комбинацию:

Вычитая почленно из первого уравнения системы второе, получаем вторую интегрируемую комбинацию:

Мы нашли два конечных уравнения

из которых легко определяется общее решение системы:

Одна интегрируемая комбинация дает возможность получить одно уравнение

связывающее независимую переменную t и неизвестные функции Такое конечное уравнение называется первым интегралом системы (8). Иначе: первым интегралом системы дифференциальных уравнений (8) называется дифференцируемая функция не равная тождественно постоянной, но сохраняющая постоянное значение на любой интегральной кривой этой системы.

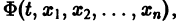
Если найдено п первых интегралов системы (8) и все они независимы, т. е. якобиан системы функций отличен от нуля:

то задача интефирования системы (8) решена (так как из системы

определяются все неизвестные функции

Системы линейных дифференциальных уравнений

Система дифференциальных уравнений называется линейной, если она линейна относительно неизвестных функций и их производных, входящих в уравнение. Система n линейных уравнений первого порядка, записанная в нормальной форме, имеет вид

или, в матричной форме,

Теорема:

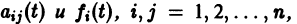
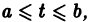
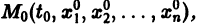
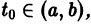
Если все функции непрерывны на отрезке то в достаточно малой окрестности каждой точки где выполнены условия теоремы существования и единственности решения задачи Коши, следовательно, через каждую такую точку проходит единственная интегральная кривая системы (1).

Действительно, в таком случае правые части системы (1) непрерывны по совокупности аргументов t, и их частные производные по ограничены, так как эти производные равны непрерывным на отрезке [а,b] коэффициентам

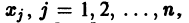
Введем линейный оператор

Тогда система (2) запишется в виде

Если матрица F — нулевая, т. е. 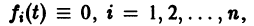на интервале (а,b), то система (2) называется линейной однородной и имеет вид

Приведем некоторые теоремы, устанавливающие свойства решений линейных систем.

Теорема:

Если X(t) является решением линейной однородной системы

то cX(t), где с — произвольная постоянная, является решением той же системы.

Теорема:

двух решений 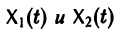однородной линейной системы уравнений является решением той же системы.

Следствие:

с произвольными постоянными коэффициентами сi решений 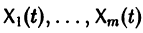линейной однородной системы дифференциальных уравнений

является решением той же системы.

Теорема:

Если 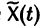есть решение линейной неоднородной системы

a Xo(t) — решение соответствующей однородной системы

будет решением неоднородной системы

Действительно, по условию,

Пользуясь свойством аддитивности оператора 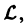получаем

Это означает, что сумма 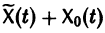есть решение неоднородной системы уравнений

Определение:

называются линейно зависимыми на интервале a

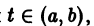
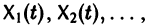
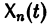
при причем по крайней мере одно из чисел аi, не равно нулю. Если тождество (5) справедливо только при то векторы называются линейно независимыми на (а, b).

Заметим, что одно векторное тождество (5) эквивалентно n тождествам:

называется определителем Вронского системы векторов

Определение:

Пусть имеем линейную однородную систему

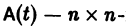
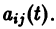
где матрица с элементами Система n решений

линейной однородной системы (6), линейно независимых на интервале а

с непрерывными на отрезке коэффициентами является линейная комбинация п линейно независимых на интервале а

() — произвольные постоянные числа).

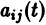
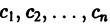
Пример:

имеет, как нетрудно проверить, решения

Эти решения линейно независимы, так как определитель Вронского отличен от нуля:

Общее решение системы имеет вид

(с1, с2 — произвольные постоянные).

Фундаментальная матрица

Квадратная матрица

столбцами которой являются линейно независимые решения 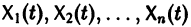системы (6), называется фундаментальной матрицей этой системы. Нетрудно проверить, что фундаментальная матрица удовлетворяет матричному уравнению

Если Х(t) — фундаментальная матрица системы (6), то общее решение системы можно представить в виде

— постоянная матрица-столбец с произвольными элементами. Полагая в (7) t = t0, имеем

Матрица 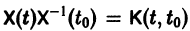называется матрицей Коши. С ее помощью решение системы (6) можно представить так:

Теорема:

О структуре общего решения линейной неоднородной системы дифференциальных уравнений. Общее решение в области 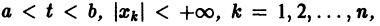линейной неоднородной системы дифференциальных уравнений

с непрерывными на отрезке коэффициентами aij(t) и правыми частями fi(t) равно сумме общего решения

соответствующей однородной системы и какого-нибудь частного решения 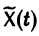неоднородной системы (2):

Метод вариации постоянных

Если известно общее решение линейной однородной системы (6), то частное решение неоднородной системы можно находить методом вариации постоянных (метод Лагранжа).

есть общее решение однородной системы (6), тогда

причем решения Xk(t) линейно независимы.

Будем искать частное решение неоднородной системы

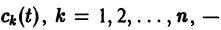
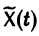
где неизвестные функции от t. Дифференцируя по t, имеем

Подставляя 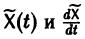в (2), получаем

то для определения 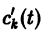получаем систему

или, в развернутом виде,

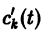
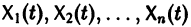
Система (10) есть линейная алгебраическая система относительно определителем которой является определитель Вронского W(t) фундаментальной системы решений . Этот определитель отличен от нуля всюду на интервале a

где 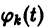— известные непрерывные функции. Интегрируя последние соотношения, находим

Подставляя эти значения 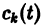в (9), находим частное решение системы (2)

(здесь под символом 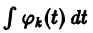понимается одна из первообразных для функции

Системы линейных дифференциальных уравнений с постоянными коэффициентами

Рассмотрим линейную систему дифференциальных уравнений

в которой все коэффициенты 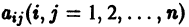— постоянные. Чаще всего такая система интегрируется сведением ее к одному уравнению более высокого порядка, причем это уравнение будет также линейным с постоянными коэффициентами. Другой эффективный метод интегрирования систем с постоянными коэффициентами — метод преобразования Лапласа.

Мы рассмотрим еще метод Эйлера интегрирования линейных однородных систем дифференциальных уравнений с постоянными коэффициентами. Он состоит в следующем.

Метод Эйлера

Будем искать решение системы

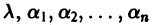
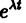
где — постоянные. Подставляя Xk в форме (2) в систему (1), сокращая на и перенося все члены в одну часть равенства, получаем систему

Для того, чтобы эта система (3) линейных однородных алгебраических уравнений с n неизвестными имела нетривиальное решение, необходимо и достаточно, чтобы ее определитель был равен нулю:

Уравнение (4) называется характеристическим. В его левой части стоит многочлен относительно степени n. Из этого уравнения определяются те значения , при которых система (3) имеет нетривиальные решения . Если все корни характеристического уравнения (4) различны, то, подставляя их по очереди в систему (3), находим соответствующие им нетривиальные решения этой системы n, следовательно, находим п решений исходной системы дифференциальных уравнений (1) в виде

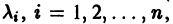
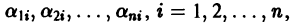
где второй индекс указывает номер решения, а первый — номер неизвестной функции. Построенные таким образом п частных решений линейной однородной системы (1)

образуют, как можно проверить, фундаментальную систему решений этой системы.

Следовательно, общее решение однородной системы дифференциальных уравнений (1) имеет вид

где произвольные постоянные.

Случай, когда характеристическое уравнение имеет кратные корни, мы рассматривать не будем.

Пример:

Ищем решение в виде

имеет корни

Система (3) для определения a1, а2 выглядит так:

Подставляя в (*) 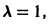получаем

откуда а21 = а11. Следовательно,

Полагая в 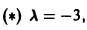находим a22 = — a12, поэтому

Общее решение данной системы:

Матричный метод

Изложим еще матричный метод интегрирования однородной системы (1). Запишем систему (1) в виде

матрица с постоянными действительными элементами

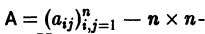
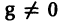
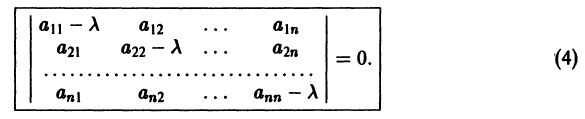
Напомним некоторые понятия из линейной алгебры. Вектор называется собственным вектором матрицы А, если

Число называется собственным значением матрицы А, отвечающим собственному вектору g, и является корнем характеристического уравнения

где I — единичная матрица.

Будем предполагать, что все собственные значения матрицы А различны. В этом случае собственные векторы g1, g2, …gn линейно независимы и существует матрица Т, приводящая матрицу А к диагональному виду, т. е. такая, что

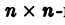
Столбцами матрицы Т являются координаты собственных векторов g1, g2 …, gn матрицы А.

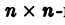
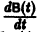
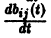
Введем еще следующие понятия. Пусть В(t) — матрица, элементы которой суть функции аргумента t, определенные на множестве . Матрица В(t) называется непрерывной на , если непрерывны на все ее элементы . Матрица В(t) называется дифференцируемой на , если дифференцируемы на все элементы этой матрицы. При этом производной матрицы называется матрица, элементами которой являются производные у соответствующих элементов матрицы В(t).

Пусть B(t) — n х n-матрица,

— вектор-столбец. Учитывая правила алгебры матриц, непосредственной проверкой убеждаемся в справедливости формулы

В частности, если В — постоянная матрица, то

так как 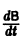есть нуль-матрица.

Теорема:

Если собственные значения матрицы А различны, то общее решение системы (7) имеет вид

где g1, g2,…, gn — собственные векторы-столбцы матрицы А, произвольные постоянные числа.

Введем новый неизвестный вектор-столбец Y(t) по формуле

где Т — матрица, приводящая матрицу А к диагональному виду. Подставляя X(t) из (11) в (7), получим систему

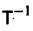
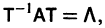
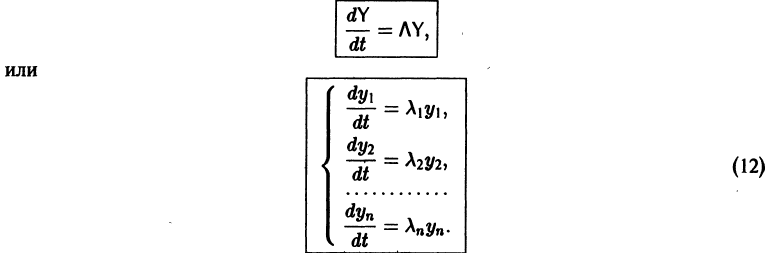
Умножая обе части последнего соотношения слева на и учитывая, что придем к системе

Мы получили систему из n независимых уравнений, которая без труда интегрируется:

Здесь 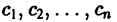— произвольные постоянные числа.

Вводя единичные n-мерные векторы-столбцы

решение Y(t) можно представить в виде

В силу (11) Х(t) = TY(t). Так как столбцы матрицы Т есть собственные векторы матрицы 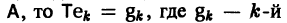собственный вектор матрицы А. Поэтому, подставляя (13) в (11), получим формулу (10):

Таким образом, если матрица А системы дифференциальных уравнений (7) имеет различные собственные значения, для получения общего решения этой системы:

1) находим собственные значения матрицы как корни алгебраического уравнения

2) находим все собственные векторы g1, g2,…, gn;

3) выписываем общее решение системы дифференциальных уравнений (7) по формуле (10).

Пример:

Матрица А системы имеет вид

1) Составляем характеристическое уравнение

Корни характеристического уравнения

2) Находим собственные векторы

Для = 4 получаем систему

откуда g11 = g12, так что

Аналогично для = 1 находим

3) Пользуясь формулой (10), получаем общее решение системы дифференциальных уравнений

Корни характеристического уравнения могут быть действительными и комплексными. Так как по предположению коэффициенты 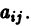системы (7) действительные, то характеристическое уравнение

будет иметь действительные коэффициенты. Поэтому наряду с комплексным корнем оно будет иметь и корень *, комплексно сопряженный с . Нетрудно показать, что если g — собственный вектор, отвечающий собственному значению , то * — тоже собственное значение, которому отвечает собственный вектор g*, комплексно сопряженный с g.

При комплексном решение

системы (7) также будет комплексным. Действительная часть

этого решения являются решениями системы (7). Собственному значению * будет отвечать пара действительных решений X1 и -Х2, т. е. та же пара, что и для собственного значения . Таким образом, паре , * комплексно сопряженных собственных значений отвечает пара действительных решений системы (7) дифференциальных уравнений.

Пусть — действительные собственные значения, — комплексные собственные значения. Тогда всякое действительное решение системы (7) имеет вид

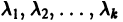
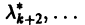
где сi — произвольные постоянные.

Пример:

1) Характеристическое уравнение системы

Его корни

2) Собственные векторы матриц

3) Решение системы

где а1, а2 — произвольные комплексные постоянные.

Найдем действительные решения системы. Пользуясь формулой Эйлера

Следовательно, всякое действительное решение системы имеет

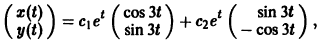
где с1, с2 — произвольные действительные числа.

Понятие о системах дифференциальных уравнений

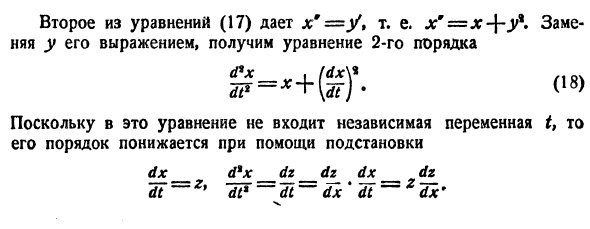
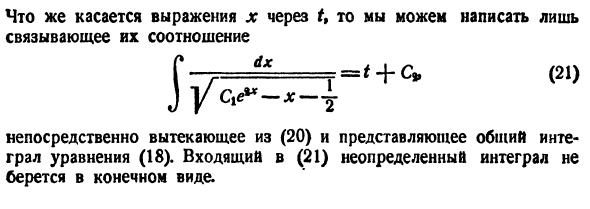
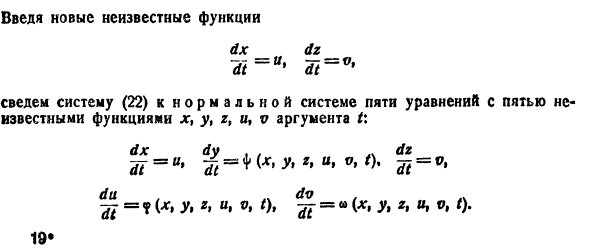
Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

23. Нормальные системы линейных однородных дифференциальных

Уравнений с постоянными коэффициентами.

При рассмотрении систем дифференциальных уравнений ограничимся случаем системы трех уравнений (n = 3). Все нижесказанное справедливо для систем произвольного порядка.

Определение. Нормальная система дифференциальных уравнений c постоянными коэффициентами называется Линейной однородной, если ее можно записать в виде:

(2)

Решения системы (2) обладают следующими свойствами:

Решения системы ищутся в виде:

Подставляя эти значения в систему (2) и перенеся все члены в одну сторону и сократив на Ekx, получаем:

Для того, чтобы полученная система имела ненулевое решение необходимо и достаточно, чтобы определитель системы был равен нулю, т. е.:

В результате вычисления определителя получаем уравнение третьей степени относительно K. Это уравнение называется Характеристическим уравнением И имеет три корня K1, K2, K3. Каждому из этих корней соответствует ненулевое решение системы (2):

Линейная комбинация этих решений с произвольными коэффициентами будет решением системы (2):

Пример. Найти общее решение системы уравнений:

Составим характеристическое уравнение:

Решим систему уравнений:

Для K1:

Полагая (принимается любое значение), получаем:

Для K2:

Полагая (принимается любое значение), получаем:

Общее решение системы:

Этот пример может быть решен другим способом:

Продифференцируем первое уравнение:

Подставим в это выражение производную У¢ =2X + 2Y из второго уравнения.

Подставим сюда У, выраженное из первого уравнения:

Обозначив , получаем решение системы:

Пример. Найти решение системы уравнений

Эта система дифференциальных уравнений не относится к рассмотренному выше типу, т. к. не является однородным (в уравнение входит независимая переменная Х).

Для решения продифференцируем первое уравнение по Х. Получаем:

Заменяя значение Z’ из второго уравнения получаем: .

С учетом первого уравнения, получаем:

Решаем полученное дифференциальное уравнение второго порядка.

Общее решение однородного уравнения:

Теперь находим частное решение неоднородного дифференциального уравнения по формуле

Общее решение неоднородного уравнения:

Подставив полученное значение в первое уравнение системы, получаем:

Пример. Найти решение системы уравнений:

Составим характеристическое уравнение:

Если принять g = 1, то решения в этом случае получаем:

Если принять g = 1, то получаем:

Если принять g = 3, то получаем:

Общее решение имеет вид:

Элементы теории устойчивости.

Теория устойчивости решений дифференциальных уравнений является одним из разделов Качественной теории дифференциальных уравнений, которая посвящена не нахождению какого – либо решения уравнения, а изучению характера поведения этого решения при изменении начальных условий или аргумента.

Этот метод особенно важен, т. к. позволяет делать вывод о характере решения без непосредственного нахождения этого решения. Т. е. даже в тех случаях, когда решение дифференциального уравнения вообще не может быть найдено аналитически.

Пусть имеется некоторое явление, описанное системой дифференциальных уравнений:

(1)

И начальные условия:

Для конкретного явления начальные условия определяются опытным путем и поэтому неточны.

Теорема. (о непрерывной зависимости решения от начальных условий)

Если правая часть дифференциального уравнения Непрерывна и по переменной у имеет ограниченную частную производную на области прямоугольника, ограниченного , то решение

, удовлетворяющее начальным условиям , непрерывно зависит от начальных данных, т. е. для любого , при котором если

то при условии, что

где

Эта теорема справедлива как для одного дифференциального уравнения, так и для системы уравнений.

Определение. Если — решение системы дифференциальных уравнений, то это решение называется Устойчивым по Ляпунову, если для любого , такое, что для любого решения той же системы, начальные условия которого удовлетворяют неравенствам

(Ляпунов Александр Михайлович (1857 – 1918) академик Петерб. АН)

Т. е. можно сказать, что решение j(t) устойчиво по Ляпунову, если близкие к нему по начальным условиям решения остаются близкими и при T ³ T0.

Если , то решение j(t) называется Асимптотически устойчивым.

Исследование на устойчивость по Ляпунову произвольного решения системы Можно свести к исследованию на устойчивость равного нулю решения некоторой другой системы, которая получена из данной заменой неизвестных функций:

(2)

Система (2) имеет тривиальное (равное нулю) решение

Теорема. Решение системы (1) устойчиво по Ляпунову тогда и только тогда, когда устойчиво по Ляпунову тривиальное решение системы (2).

Это тривиальное решение называется Положением равновесия Или Точкой покоя.

Определение. Точка покоя Системы (2) устойчива по Ляпунову, если для любого такое, что из неравенства

.

Теорема. (Теорема Ляпунова). Пусть задана система

Имеющая тривиальное решение .

Пусть существует дифференцируемая функция , удовлетворяющая условиям:

1) ³0 и V = 0 только при у1 = у2 = … = уN =0, т. е. функция V Имеет минимум в начале координат.

2) Полная производная функции V Вдоль фазовой траектории (т. е. вдоль решения Yi(T) системы (1)) удовлетворяет условию:

при

Тогда точка покоя устойчива по Ляпунову.

Если ввести дополнительное требование, чтобы вне сколь угодно малой окрестности начала координат выполнялось условие

Где B — постоянная величина, то точка покоя асимптотически устойчива.

Функция V называется Функцией Ляпунова.

Классификация точек покоя.

Рассмотрим систему двух линейных дифференциальных уравнений с постоянными коэффициентами

Характеристическое уравнение этой системы имеет вид:

Рассмотрим следующие возможные случаи:

1) Корни характеристического уравнения действительные, отрицательные и различные.

Точка покоя будет устойчива. Такая точка покоя называется Устойчивым узлом.

2) Корни характеристического уравнения действительны и

или .

В этом случае точка покоя также будет устойчива.

3) Хотя бы один из корней положителен.

В этом случае точка покоя Неустойчива, и такую точку называют Неустойчивым седлом.

4) Оба корня характеристического уравнения положительны .

В этом случае точка покоя Неустойчива, и такую точку называют Неустойчивым узлом.

Если полученного решения Системы исключить параметр T, то полученная функция дает траекторию движения в системе координат XOY.

Возможны следующие случаи:

b b

Устойчивый узел. Неустойчивый узел. Седло.

5) Корни характеристического уравнения комплексные .

Если Р = 0, т. е. корни чисто мнимые, то точка покоя (0, 0) устойчива по Ляпунову.

Такая точка покоя называется Центром.

Если P 0, то точка покоя неустойчива и называется Неустойчивым фокусом.

Уравнения математической физики.

Уравнения в частных производных.

Определение. Дифференциальным уравнением в частных производных Называется уравнение относительно неизвестной функции нескольких переменных, ее аргументов и ее частных производных различных порядков.

Порядком Дифференциального уравнения в частных производных называется порядок старшей производной, входящей в это уравнение. Решением Уравнения будет некоторая функция , которая обращает уравнение в тождество.