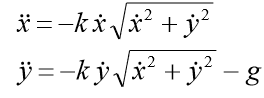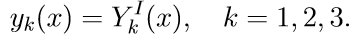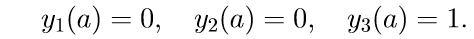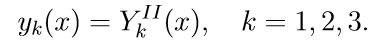Системы дифференциальных уравнений в приложениях
Дифференциальные уравнения широко используются для моделирования реальных систем, зависящих от времени, в частности, для описания и исследования экономических и биологических систем.
В динамике популяций есть много примеров, когда изменение численности популяций во времени носит колебательный характер. Одним из самых известных примеров описания динамики взаимодействующих популяций являются уравнения Вольтерра—Лотка. Рассмотрим модель взаимодействия хищников и их добычи, когда между особями одного вида нет соперничества.
Пусть x1 и x2 — число жертв и хищников соответственно. Предположим, что относительный прирост жертв x1‘/x1 равен a-bx2, a>0, b>0, где a — скорость размножения жертв в отсутствие хищников, —bx2 — потери от хищников. Развитие популяции хищников зависит от количества пищи (жертв), при отсутствии пищи ( x1=0 ) относительная скорость изменения популяции хищников равна 

Таким образом, система Вольтерра—Лотка имеет вид: 
где a, b, c, d >0.
Рассмотренная модель может описывать поведение конкурирующих фирм, рост народонаселения, численность воюющих армий, изменение экологической обстановки, развитие науки и пр.
Рассмотрим фазовый портрет системы Вольтерра—Лотка для a=4, b=2.5, c=2, d=1 и графики ее решения с начальным условием x1(0)=3, x2(0)=1, построенные программой ОДУ.
Видно, что процесс имеет колебательный характер. При заданном начальном соотношении числа особей обоих видов 3 : 1 , обе популяции сначала растут. Когда число хищников достигает величины b=2.5 , популяция жертв не успевает восстанавливаться и число жертв начинает убывать. Уменьшение количества пищи через некоторое время начинает сказываться на популяции хищников и когда число жертв достигает величины x1=c/d =2 (в этой точке x2‘=0), число хищников тоже начинает сокращаться вместе с сокращением числа жертв. Сокращение популяций происходит до тех пор, пока число хищников не достигнет величины x2=a/b =1.6 (в этой точке x1‘=0).С этого момента начинает расти популяция жертв, через некоторое время пищи становится достаточно, чтобы обеспечить прирост хищников, обе популяции растут, и . процесс повторяется снова и снова. На графике четко виден периодический характер процесса. Количество жертв и хищников колеблется возле величин x1=2, x2=1.6 соответственно (дробные числа здесь не означают “половину волка”, величины могут измеряться в сотнях, тысячах и т.п.). Периодичность процесса явственно видна на фазовой плоскости — фазовая кривая (x1(t), x2(t)) — замкнутая линия. Самая левая точка, этой кривой, — это точка, в которой число жертв достигает наименьшего значения. Самая правая точка x1=4, x2=1.6 , — точка пика популяции жертв. Между этими точками количество хищников сначала убывает, до нижней точки фазовой кривой,x1=2 , где достигает наименьшего значения, а затем растет до верхней точки фазовой кривой (x1=2, x2=2.5). Фазовая кривая охватывает точку x1=2, x2=1.6.
На языке дифференциальных уравнений это означает, что система имеет стационарное состояние
x1‘ =0, x2‘ =0,
которое достигается в точке x1=2, x2=1.6. Если в начальный момент система находилась в стационарной точке, то решения x1(t), x2(t) не будут изменяться во времени, останутся постоянными. Всякое же другое начальное состояние приводит к периодическому колебанию решений. Неэллиптичность формы траектории, охватывающей центр, отражает негармонический характер колебаний.
Рассмотренная модель может описывать поведение конкурирующих фирм, рост народонаселения, численность воюющих армий, изменение экологической обстановки, развитие науки и т.п.
Рассмотрим модель конкурирующих видов с “логистической поправкой”: 
В этом случае поведение решений в окрестности стационарной точки меняется в зависимости от величины и знака параметра a.
Рассмотрим фазовый портрет системы Вольтерра—Лотка для a =0.1, a=4, b=2.5, c=2, d=1 и графики ее решения с начальным условием x1(0)=3, x2(0)=1, построенные программой ОДУ.
Видно, что в этом случае стационарная точка превращается в устойчивый фокус, а решения — в затухающие колебания. При любом начальном условии состояние системы через некоторое время становится близким к стационарному и стремится к нему при 
Графики решений и фазовая кривая при отрицательном значении параметра a, a =-0.1, приведены ниже.
Как видно, в этом случае стационарная точка является неустойчивым фокусом и амплитуда колебаний численности видов растет. В этом случае как бы близко ни было начальное состояние к стационарному, с течением времени состояние системы будет сильно отличаться от стационарного.
ПРИМЕР 2. Модель «хищник-жертва» с логистической поправкой.
На примере модели Вольтерра—Лотка и модели Вольтерра—Лотка с логистической поправкой было продемонстрировано одно из важнейших качественных свойств центров — они легко разрушаются даже при самых малых изменениях правой части. Большинство моделей является идеализацией действительности; в них внимание сосредоточено на некоторых основных переменных и соотношениях между ними. Поэтому устойчивость моделей относительно малых возмущений чрезвычайно важна в приложениях. Модели, не чувствительные к малым возмущениям, называются грубыми.
Модель Вольтерра—Лотка неустойчива относительно возмущений, поскольку ее стационарное состояние — центр.
Существует другой вид моделей, в которых возникают незатухающие колебания, — это модели, имеющие на фазовых портретах предельные циклы. Такая модель существует для системы конкурирующих видов — это модель Холлинга—Тэннера.
Скорость роста популяции жертв x‘1 в этой модели равна сумме трех величин:
- скорости размножения в отсутствие хищников — r x1;
- влиянию межвидовой конкуренции за пищу при ограниченных ресурсах (для случая конкурирующих производителей это влияние ограниченных сырьевых ресурсов) —
- влиянию хищников , в предположении, что хищник перестает убивать, когда насыщается —
Скорость роста популяции хищников x‘2 строится так же, как в модели Вольтерра—Лотка, в предположении, что жертвы встречаются редко. Если для поддержания жизни одного хищника нужно J жертв, то популяция из x1 жертв сможет обеспечить пищей x1/J хищников. Модель роста популяции хищников, в которой их число не может превысить эту критическую величину, имеет вид 
Таким образом, имеем модель Холлинга—Тэннера: 
где r, s, K, D, J > 0.
Можно показать, что при 
на фазовом портрете системы будет устойчивый предельный цикл. Ниже приведено решение системы при r=1, K=7, w=1, D=1, s=0.2, J=0.5 и двух различных начальных состояниях и фазовый портрет системы, построенные программой ОДУ.
Модель выравнивания цен по уровню актива интересна тем, что в ней можно наблюдать гармонические колебания решений возле стационарного состояния. Предположим, что изменение уровня актива q пропорционально разности между предложением s и спросом d, т.е. q‘=k(s—d), k > 0. Предположим далее, что изменение цены p пропорционально отклонению актива q от некоторого фиксированного уровня q0 так, что p‘=-m(q—q0 ) , m > 0. Таким образом, модель выравнивания цен по уровню актива имеет вид
q‘ = k(s(p) — d(p)),
p‘ = — m(q—q0).
Видно, что цена и актив колеблются возле стационарного состояния. Фазовая траектория представляет собой эллипс, охватывающий стационарную точку. Это означает, что колебания актива и цены — гармонические.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Численное решение математических моделей объектов заданных системами дифференциальных уравнений
Введение:
При математическом моделировании ряда технических устройств используются системы дифференциальных нелинейных уравнений. Такие модели используются не только в технике, они находят применение в экономике, химии, биологии, медицине, управлении.
Исследование функционирования таких устройств требуют решения указанных систем уравнений. Поскольку основная часть таких уравнений являются нелинейными и нестационарными, часто невозможно получить их аналитическое решение.
Возникает необходимость использовать численные методы, наиболее известным из которых является метод Рунге — Кутты [1]. Что касается Python, то в публикациях по численным методам, например [2,3], данных по применение Рунге — Кутты крайне мало, а по его модификации — методу Рунге-Кутта-Фельберга вообще нет.
В настоящее время, благодаря простому интерфейсу, наибольшее распространение в Python имеет функцию odeint из модуля scipy.integrate. Вторая функция ode из этого модуля реализует несколько методов, в том числе и упомянутый пятиранговый метод Рунге-Кутта-Фельберга, но, вследствие универсальности, имеет ограниченное быстродействие.
Целью настоящей публикации является сравнительный анализ перечисленных средств численного решения систем дифференциальных уравнений с модифицированным автором под Python методом Рунге-Кутта-Фельберга. В публикации так же приведены решения по краевым задачам для систем дифференциальных уравнений (СДУ).
Краткие теоретические и фактические данные по рассматриваемым методам и программным средствам для численного решения СДУ
Для одного дифференциального уравнения n – го порядка, задача Коши состоит в нахождении функции, удовлетворяющей равенству:
и начальным условиям
Перед решением эта задача должна быть переписана в виде следующей СДУ
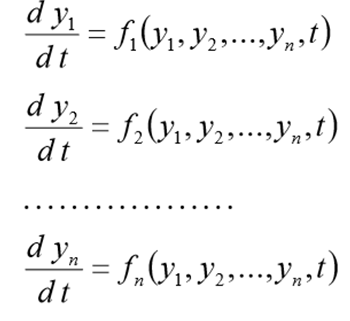
с начальными условиями
Модуль имеет две функции ode() и odeint(), предназначенные для решения систем обыкновенных дифференциальных уравнений (ОДУ) первого порядка с начальными условиями в одной точке (задача Коши). Функция ode() более универсальная, а функция odeint() (ODE integrator) имеет более простой интерфейс и хорошо решает большинство задач.
Функция odeint() имеет три обязательных аргумента и много опций. Она имеет следующий формат odeint(func, y0, t[,args=(), . ]) Аргумент func – это имя Python функции двух переменных, первой из которых является список y=[y1,y2. yn], а второй – имя независимой переменной.
Функция func должна возвращать список из n значений функций 
Второй аргумент y0 функции odeint() является массивом (или списком) начальных значений 
Третий аргумент является массивом моментов времени, в которые вы хотите получить решение задачи. При этом первый элемент этого массива рассматривается как t0.
Функция odeint() возвращает массив размера len(t) x len(y0). Функция odeint() имеет много опций, управляющих ее работой. Опции rtol (относительная погрешность) и atol (абсолютная погрешность) определяют погрешность вычислений ei для каждого значения yi по формуле
Они могут быть векторами или скалярами. По умолчанию
Вторая функция модуля scipy.integrate, которая предназначена для решения дифференциальных уравнений и систем, называется ode(). Она создает объект ОДУ (тип scipy.integrate._ode.ode). Имея ссылку на такой объект, для решения дифференциальных уравнений следует использовать его методы. Аналогично функции odeint(), функция ode(func) предполагает приведение задачи к системе дифференциальных уравнений вида (1) и использовании ее функции правых частей.
Отличие только в том, что функция правых частей func(t,y) первым аргументом принимает независимую переменную, а вторым – список значений искомых функций. Например, следующая последовательность инструкций создает объект ODE, представляющий задачу Коши.
При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.
При численном решении задачи Коши
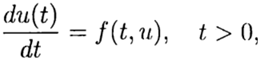

по известному решению в точке t =0 необходимо найти из уравнения (3) решение при других t. При численном решении задачи (2),(3) будем использовать равномерную, для простоты, сетку по переменной t с шагом т > 0.
Приближенное решение задачи (2), (3) в точке 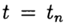

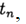


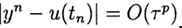

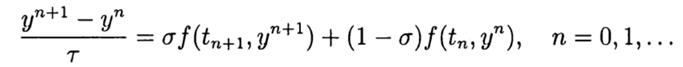
При 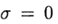
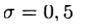
Явные схемы второго и более высокого порядка аппроксимации удобно строить, ориентируясь на метод предиктор-корректор. На этапе предиктора (предсказания) используется явная схема
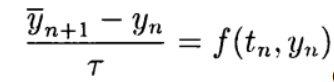
а на этапе корректора (уточнения) — схема
В одношаговых методах Рунге—Кутта идеи предиктора-корректора реализуются наиболее полно. Этот метод записывается в общем виде:

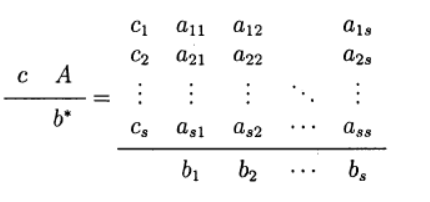
Формула (6) основана на s вычислениях функции f и называется s-стадийной. Если 
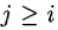

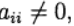

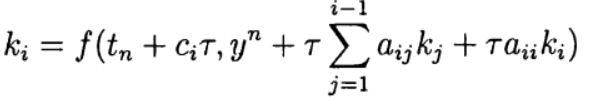
О таком методе Рунге—Кутта говорят как о диагонально-неявном. Параметры 
Одним из наиболее распространенных является явный метод Рунге—Кутта четвертого порядка

Метод Рунге—Кутта— Фельберга
Привожу значение расчётных коэффициентов 
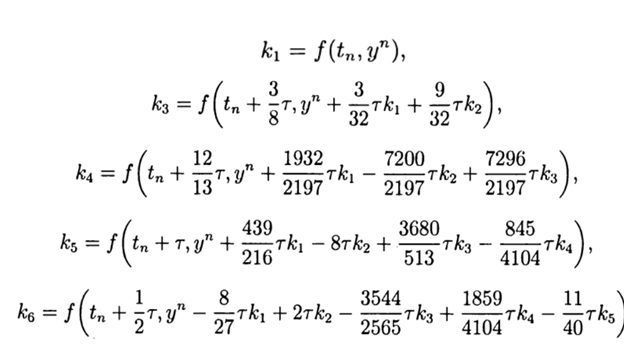
С учётом(9) общее решение имеет вид:
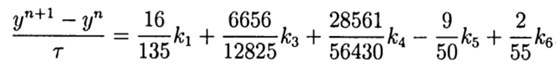
Это решение обеспечивает пятый порядок точности, остаётся его адаптировать к Python.
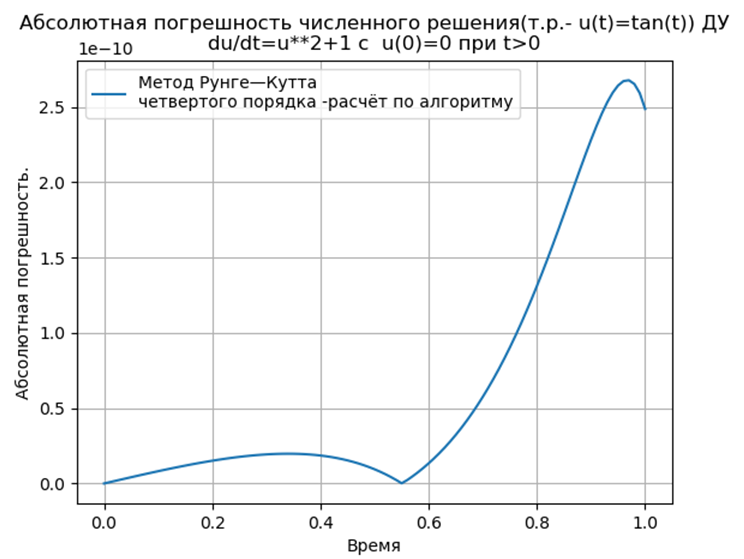
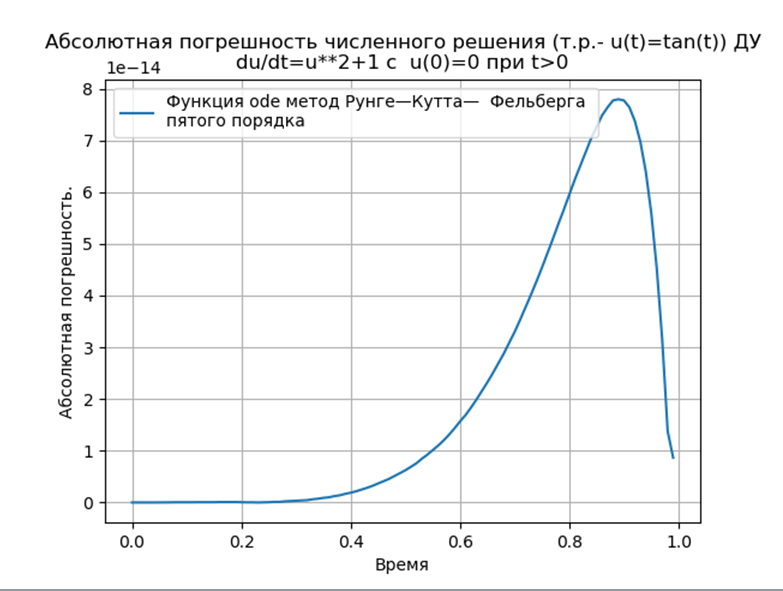
Вычислительный эксперимент по определению абсолютной погрешности численного решения нелинейного дифференциального уравнения  с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
Адаптированные к Python методы Рунге—Кутта и Рунге—Кутта— Фельберга имеют меньшую абсолютную, чем решение с применением функции odeint, но большую, чем с использованием функции edu. Необходимо провести исследование быстродействия.
Численный эксперимент по сравнению быстродействия численного решения СДУ при использовании функции ode с атрибутом dopri5 (метод Рунге – Кутты 5 порядка) и с использованием адаптированного к Python метода Рунге—Кутта— Фельберга
Сравнительный анализ проведём на примере модельной задачи, приведенной в [2]. Чтобы не повторять источник, приведу постановку и решение модельной задачи из [2].
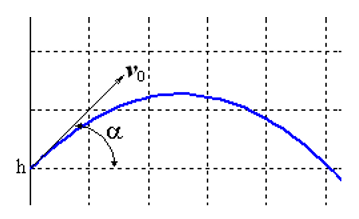
Решим задачу Коши, описывающую движение тела, брошенного с начальной скоростью v0 под углом α к горизонту в предположении, что сопротивление воздуха пропорционально квадрату скорости. В векторной форме уравнение движения имеет вид
где 



Особенность этой задачи состоит в том, что движение заканчивается в заранее неизвестный момент времени, когда тело падает на землю. Если обозначить 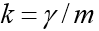
К системе следует добавить начальные условия: 

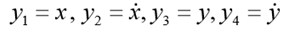
Для модельной задачи положим 
Flight time = 1.2316 Distance = 5.9829 Height =1.8542
Flight time = 1.1016 Distance = 4.3830 Height =1.5088
Flight time = 1.0197 Distance = 3.5265 Height =1.2912
Flight time = 0.9068 Distance = 2.5842 Height =1.0240
Время на модельную задачу: 0.454787
Для реализации средствами Python численного решения СДУ без использования специальных модулей, мною была предложена и исследована следующая функция:
def increment(f, t, y, tau
k1=tau*f(t,y)
k2=tau*f(t+(1/4)*tau,y+(1/4)*k1)
k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2)
k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3)
k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4)
k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5)
return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6
Функция increment(f, t, y, tau) обеспечивает пятый порядок численного метода решения. Остальные особенности программы можно посмотреть в следующем листинге:
Время на модельную задачу: 0.259927
Предложенная программная реализация модельной задачи без использования специальных модулей имеет почти в двое большее быстродействие, чем с функцией ode, однако нельзя забывать, что ode имеет более высокую точность численного решения и возможности выбора метода решения.
Решение краевой задачи с поточно разделёнными краевыми условиями
Приведем пример некоторой конкретной краевой задачи с поточно разделенными краевыми условиями:
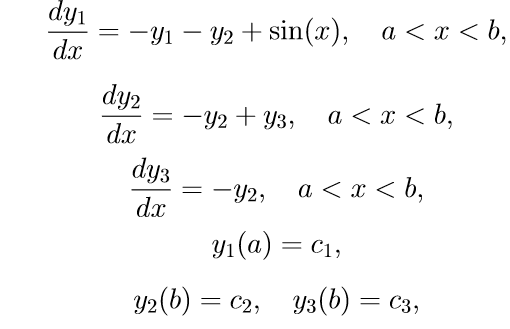
Для решения задачи (11) используем следующий алгоритм:
1. Решаем первые три неоднородные уравнения системы (11) с начальными условиями 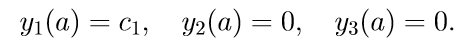
Введем обозначение для решения задачи Коши:
2. Решаем первые три однородные уравнения системы (11) с начальными условиями 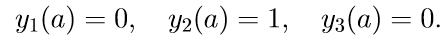
Введем обозначение для решения задачи Коши:
3. Решаем первые три однородные уравнения системы (11) с начальными условиями
Введем обозначение для решения задачи Коши:
4. Общее решение краевой задачи (11) при помощи решений задач Коши записывается в виде линейной комбинации решений: 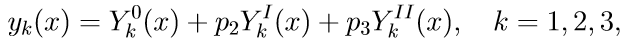
где p2, p3 — некоторые неизвестные параметры.
5. Для определения параметров p2, p3, используем краевые условия последних двух уравнений (11), то есть условия при x = b. Подставляя, получим систему линейных уравнений относительно неизвестных p2, p3:

Решая (12), получим соотношения для p2, p3.
По приведенному алгоритму с применением метода Рунге—Кутта—Фельберга получим следующую программу:
y0[0]= 0.0
y1[0]= 1.0
y2[0]= 0.7156448588231397
y3[0]= 1.324566562303714
y0[N-1]= 0.9900000000000007
y1[N-1]= 0.1747719838716767
y2[N-1]= 0.8
y3[N-1]= 0.5000000000000001
Время на модельную задачу: 0.070878
Вывод
Разработанная мною программа отличается от приведенной в [3] меньшей погрешностью, что подтверждает приведенный в начале статьи сравнительный анализ функции odeint с реализованным на Python метода Рунге—Кутта—Фельберга.
3. Н.М. Полякова, Е.В. Ширяева Python 3. Создание графического интерфейса пользователя (на примере решения методом пристрелки краевой задачи для линейных обыкновенных дифференциальных уравнений). Ростов-на-Дону 2017.
Системы дифференциальных уравнений в приложениях
Если строка в кавычках «. «, то найдутся страницы со словосочетанием в точно такой форме.
Если слова указаны через пробел или оператор «&», то найдутся страницы, содержащие все введенные слова в одном предложении.
Если указано несколько слов через оператор «|», то найдутся страницы, содержащие любое из введенных слов.
Если указано два слова через оператор «
», то найдутся страницы, содержащие первое, но не содержащие второе слово в одном предложении.
По вашему запросу ничего не найдено.
Убедитесь, что слова написаны без ошибок или попробуйте выбрать другие значения.
http://habr.com/ru/post/418139/
http://www.mathedu.ru/text/amelkin_differentsialnye_uravneniya_v_prilozheniyah_1987/














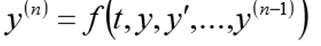
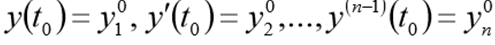


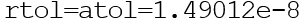
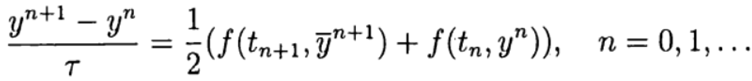
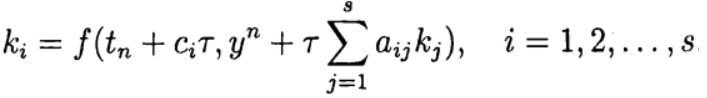
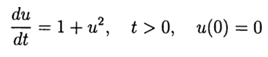 с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга