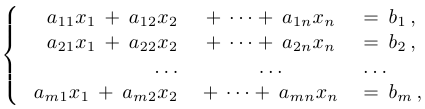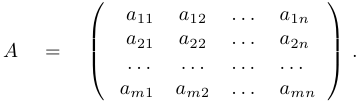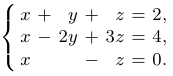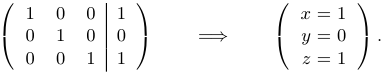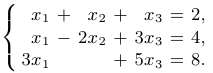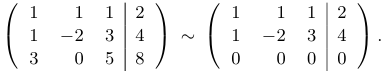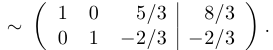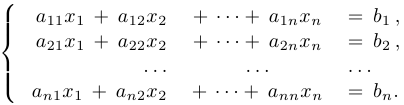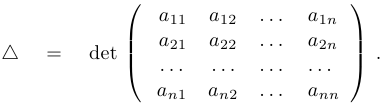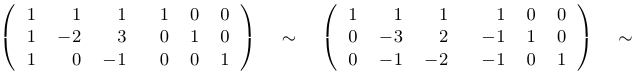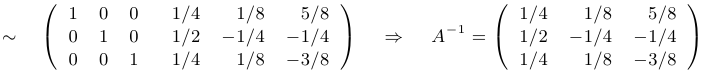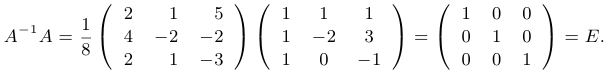Курсовая работа: Решение системы линейных уравнений
| Название: Решение системы линейных уравнений Раздел: Рефераты по информатике, программированию Тип: курсовая работа Добавлен 01:57:05 25 июня 2010 Похожие работы Просмотров: 2073 Комментариев: 21 Оценило: 5 человек Средний балл: 4.2 Оценка: неизвестно Скачать | |||||||||||||||||||||||||||||
 |
Метод Зейделя сходится примерно так же, как геометрическая прогрессия со знаменателем || G | | . Если норма матрицы G близка к 1, то скорость сходимости очень медленная. Для ускорения сходимости используется метод релаксации . Суть его в том, что полученное по методу Зейделя очередное значение пересчитывается по формуле:
Здесь 0 1 – верхняя релаксация . Параметр w подбирают так, чтобы сходимость метода достигалась за минимальное число итераций.
Метод Зейделя является одношаговым итерационным методам , когда для нахождения x ( k +1) требуется помнить только одну предыдущую итерацию x ( k ) .
Погрешность итерации вычисляется по формуле:
n — порядок матрицы A.
Если d меньше заданной точности e, то итерационный процесс прекращают.
Элементы главной диагонали называются главными. Заметим, что если в ходе расчётов по данному алгоритму на главной диагонали окажется нулевой элемент, то произойдет сбой программы. Для того, чтобы избежать этого, следует перестановку строк таким образом, чтобы на главной диагонали находились максимальные элементы строк. Т. е., если в k-й строке максимальным является i-й элемент, необходимо поменять местами k-ю и i-ю строки, и поменять местами соответствующие элементы вектора b. Такой выбор главного элемента необходим для сходимости итерационного процесса.
Приведём блок-схему реализации данного метода:
 |
 |
 |
 |
 |
 | ||
 | ||
 |  | |
 | ||
 |  |  |
 |  |
 |
 | ||
 | ||
3. Анализ результатов.
Скорость сходимости итерационного процесса зависит от заданной матрицы коэффициентов. В зависимости от вида исходных данных( матрицы коэффициентов и матрицы b) программа подбирает оптимальный параметр релаксации w(при котором решение достигается за минимальное число итераций).
Для достижения наивысшей скорости сходимости итерационного процесса для уравнения, заданного на рис.3 программой был выбран параметр релаксации w=1,26. Таким образом, была применена верхняя релаксация. Заданная точность e=0,0001 была достигнута за 40 итераций.
График зависимости количества итераций от параметра релаксации приведен на рис 1.
 |
Рис. 1
Для достижения наивысшей скорости сходимости итерационного процесса для уравнения, заданного на рис.4 программой был выбран параметр релаксации w=0,98. Таким образом, была применена нижняя релаксация. Заданная точность e=0,0001 была достигнута за 17 итераций. График зависимости количества итераций от параметра релаксации приведен на рис 2.
 |
Рис. 2
Правильность решения СЛАУ была проверена с помощью программного пакета Mathcad 2000 professional. Отметим, что программа даёт правильное решение СЛАУ почти во всех случаях, когда каждый элемент главной диагонали является максимальным в своей строке.
Программа, разработанная в данной курсовой работе, реализует метод Зейделя для решения СЛАУ 6-го порядка. Она даёт гарантированно правильное решение системы линейных уравнений, если каждый элемент главной диагонали матрицы коэффициентов является единственным максимальным в своей строке, ненулевым, либо справедливы условия: максимальный элемент строки является единственным максимальным в своём столбце, ненулевым, а ни один из остальных элементов столбца не является максимальным в своей строке, все элементы каждой строки кроме максимального одинаковы.
При исходных данных:
была достигнута точность 0,0001 в решении:
 |
за 2 итерации при параметре релаксации w=0,97.
Программа строит график зависимости количества итераций от параметра релаксации для данной СЛАУ, находит параметр релаксации w, при котором решение достигается за минимальное количество итераций и, разумеется, само решение. Программа проста в эксплуатации и нетребовательна к ресурсам. Реализованная в современной среде разработки Delphi 5.0, она без труда может быть доработана или исправлена.
Недостатки программы: 1) применима не для всех систем линейных уравнений; 2)оптимальный параметр релаксации w вычисляется методом подбора, и, поэтому, количество итераций, требуемое для его отыскания достаточно велико(около 18000), однако, для современных ПК, это не является затруднением.
Список использованной литературы
1. Волков Е.А. Численные методы. ¾ М.: Наука, 1987. ¾ 254 с.
2. Калиткин Н.Н. Численные методы. ¾ М.: Наука, 1978. ¾ 512 с.
3. Мудров А.Е. Численные методы для ПЭВМ на языках БЕЙСИК, ФОРТРАН и ПАСКАЛЬ. ¾ Томск, МП «Раско», 1992. ¾270 с.
4. Самарский А.А., Гулин А.В. Численные методы. ¾ М.: Наука, 1989. ¾432с.
5. Кэнту М. Delphi 4 для профессионалов ¾ СПб: «Питер», 1999 ¾1200с.
6. Delphi 5.0 help.
Приложение(распечатка программы, результатов)
Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs,
Grids, StdCtrls, ComCtrls, ToolWin, Menus, Unit1, TeEngine, Series,
Системы линейных уравнений — курсовая работа (Теория) по математике
 |
|
Тезисы:
- Таким образом, однородная система линейных уравнений всегда совместна.
- Матрицы дают возможность кратко записать систему линейных уравнений.
- Основные понятия и теоремы систем линейных уравнений.
- Критерий совместности общей системы линейных уравнений.
- Однородная система п линейных уравнений с n неизвестными.
- Основные методы решения систем линейных уравнений.
- Матричный метод решения систем линейных уравнений.
- В самом общем случае система линейных уравнений имеет следующий вид.
- Однородная система п линейных уравнений с п неизвестными имеет вид.
- Рассмотрим систему 3-х линейных уравнений с тремя неизвестными.
Похожие работы:
32 Кб / 11 стр / 267 слов / 1836 букв / 20 ноя 2010
2 Мб / 39 стр / 2705 слов / 18573 букв / 1 окт 2011
74 Кб / 19 стр / 1194 слов / 8848 букв / 23 окт 2013
79 Кб / 30 стр / 2963 слов / 15846 букв / 1 дек 2012
84 Кб / 45 стр / 5589 слов / 49671 букв / 1 ноя 2012
137 Кб / 33 стр / 3727 слов / 21749 букв / 13 янв 2020
250 Кб / 28 стр / 1954 слов / 12842 букв / 10 дек 2015
89 Кб / 21 стр / 2467 слов / 17346 букв / 24 янв 2019
378 Кб / 39 стр / 5063 слов / 36156 букв / 1 авг 2015
116 Кб / 14 стр / 525 слов / 4034 букв / 31 окт 2014
Системы линейных уравнений
Мы рассматриваем системы линейных алгебраических уравнений вида
где 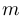
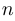
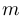
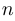
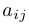
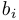
Матрицей системы называется следующая матрица (прямоугольная таблица чисел), составленная из коэффициентов системы
Расширенной матрицей системы называется матрица системы, к которой справа приписан столбец свободных членов. Обычно его отделяют от матрицы системы вертикальной чертой:
Решением системы называется такой набор постоянных 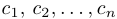
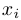
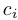
Системы линейных уравнений классифицируются по числу решений следующим образом:
- совместная система — система линейных уравнений, имеющая хотя бы одно решение;
- несовместная (противоречивая) система — система, не имеющая ни одного решения;
- определенная система — система, имеющая единственное решение;
- неопределенная система — система, имеющая более одного решения.
Существуют два основных способа решения линейных систем: метод Гаусса и, если 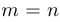
Метод Гаусса.
Для решения системы не обязательно «таскать за собой» полную запись системы — достаточно работать с расширенной матрицей. При этом с ней можно производить операции, которые называются элементарными преобразованиями. К таковым относятся следующие действия со строками расширенной матрицы:
- перемена мест строк;
- умножение одной из строк на число, отличное от нуля;
- прибавление к одной из строк линейной комбинации нескольких других.
Отметим, что лучше не производить операции со столбцами расширенной матрицы, ибо без этих преобразований всегда можно обойтись, хотя они иногда и упрощают вид системы. Неудобство, связанное с ними, состоит в том, что при этом приходится «вести протокол», чтобы затем правильно интерпретировать ответ. Например, перемена мест столбцов означает соответствующее изменение нумерации переменных и после получения ответа ее надо восстановить.
Если в процессе преобразований появляется нулевая строчка, то мы ее вычеркиваем, уменьшая количество строк на единицу.
При элементарных преобразованиях может получиться матрица, у которой есть строчка, все элементы которой слева от черты равны нулю, а справа стоит ненулевое число. В этом случае мы отмечаем, что система несовместна (противоречива), то есть не имеет решения. То же самое происходит, если совпадают две строчки за исключением свободных членов, которые различны. Например, несовместной является следующая система:
Желательной целью цепочки элементарных преобразований является приведение расширенной матрицы к такому виду, что на месте основной матрицы системы стоит единичная матрица, то есть единичная матрица стоит слева от черты в расширенной матрице. В этом случае процедура закончена и система является определенной, то есть имеет одно решение (один набор значений переменных). Этот набор переменных указан столбцом свободных членов.
Пример 1.
Выпишем расширенную матрицу системы и сделаем пару элементарных преобразований:
Из первой и второй строк мы вычли третью. После этого все элементы второй строки разделим на 2 и полученную строку сложим с первой, записав сумму на место первой строки:
В получившейся матрице все элементы первой строки сократим на 4, элементы второй строки умножим на —1 и затем поменяем первую и третью строки местами, чтобы получилась треугольная матрица, то есть матрица, у которой все элементы ниже главной диагонали равны 0:
Наконец, мы приводим матрицу к диагональному виду и выписываем ответ:
Таким образом, мы нашли некоторое решение. Это означает, что система совместна.
Найденное решение оказалось единственным. Это означает, что система определённа.
Если к единичной матрице не удается привести левую часть, но в то же время система не является противоречивой, то в этом случае система является совместной, но неопределенной, то есть имеет бесконечное множество решений. В этом случае одной или нескольким переменным можно придать произвольные значения, которые обычно не фиксируются, условно обозначаются буквами, например 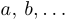
Пример 2.
Выпишем расширенную матрицу системы и сделаем естественные преобразования:
Из третьей строки мы вычли вторую и удвоенную первую. После этого вычеркнем нулевую строку и из второй строки вычтем первую. Затем выделим единичную матрицу коэффициентов перед 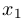
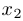
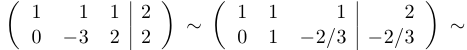
Отсюда следует, что 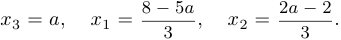
Таким образом, система имеет решение, то есть она совместна. Найденное решение оказалось не единственным. Это означает, что система является неопределенной. Если ставится задача найти какое-нибудь решение, то мы можем положить а равным, например, 1, и тогда 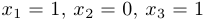
Правило Крамера.
Этот метод используется для решения систем в случае, когда число уравнений совпадает с числом неизвестных, то есть 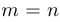
Обозначим через 
Предполагается, что определитель системы не равен нулю (в противном случае система является либо неопределенной, либо несовместной). Обозначим через 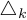
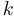
Формулы Крамера: 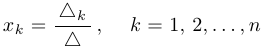
Теорема Крамера. Рассматривается линейная система, в которой число уравнений совпадает с числом неизвестных.
Если определитель матрицы системы равен нулю, то система является либо несовместной, либо неопределенной.
Если определитель матрицы системы не равен нулю, то система является совместной и определенной, причем решения системы находятся по формулам Крамера.
Обратная матрица.
Квадратная матрица 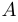
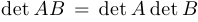
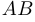
Пусть 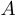

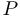
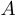
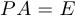
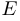
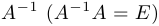
Теорема об обратной матрице. Квадратная матрица 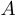
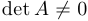
1) 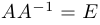
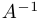
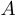
2) обратная матрица (если она существует) единственна:
3) если 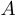
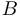
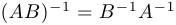
4) 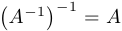
Метод Гаусса нахождения обратной матрицы.
Существует несколько способов нахождения обратной матрицы. Покажем, как это делается методом Гаусса.
Для произвольной квадратной матрицы 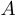
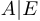
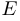
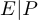
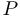
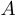
Пример 3.
Найти матрицу, обратную к матрице 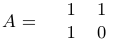
Решение:
Выпишем спаренную матрицу, вычтем из первой строки вторую, а затем поменяем строки местами:
Таким образом, обратная матрица найдена: 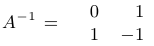
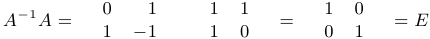
Пример 4.
Найти матрицу, обратную к матрице 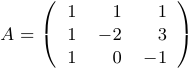
Решение:
Выпишем спаренную матрицу и сделаем пару элементарных преобразований:
Из второй и третьей строк мы вычли первую. После этого у всех элементов третьей строки поменяем знак и трижды прибавим ко второй строке. Далее разделим вторую строку на 8, а затем вычтем вторую строку из первой и дважды из третьей)


Таким образом, обратная матрица найдена. Произведем проверку:
Матричная запись решения линейной системы.
Рассмотрим линейную систему, в которой число уравнений совпадает с числом неизвестных, то есть систему вида
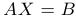
Если 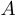
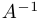
Это и есть решение системы.
На этой странице найдёте другие готовые курсовые работы во высшей математике:
Можете посмотреть другие готовые курсовые работы по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://studentlib.com/kursovaya_rabota_teoriya-230068-sistemy_lineynyh_uravneniy.html
http://lfirmal.com/kursovaya-rabota-na-temu-sistemyi-linejnyih-uravnenij/
 .
.
 .
. или
или  .
. .
. .
. , то метод Якоби сходится при любом начальном приближении x (0 ) .
, то метод Якоби сходится при любом начальном приближении x (0 ) . ,
, , или
, или ,
, .
. .
. .
. ,
, .
. или
или  .
. .
.
 , то метод Зейделя сходится при любом начальном приближении x (0 ) .
, то метод Зейделя сходится при любом начальном приближении x (0 ) .