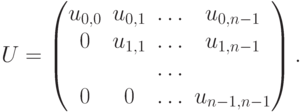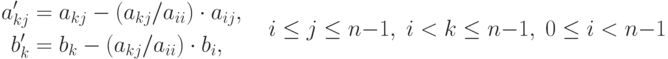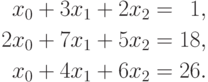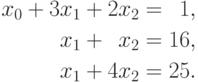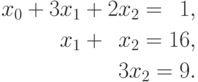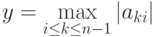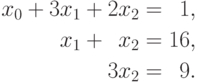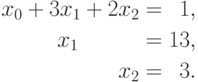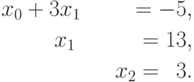Системы линейных уравнений параллельных алгоритмов
В данном разделе приводятся примеры параллельных алгоритмов решения следующих задач: умножения матрицы на матрицу, задача Дирихле, решение систем линейных уравнений (СЛАУ) методом Гаусса и методом простой итерации. Здесь рассматривается простой вариант сеточной задачи (задача Дирихле), когда шаг сетки в пространстве вычислений одинаков и не меняется в процессе вычислений. При динамически изменяющемся шаге сетки потребовалось бы решать такую задачу параллельного программирования, как перебалансировка вычислительного пространства между компьютерами, для выравнивания вычислительной нагрузки компьютеров, а эта задача здесь не рассматривается.
В этой главе приводятся только общие схемы решения указанных задач, а тексты программ приведены в следующих разделах, т.к. для понимания общих схем решения знать MPI не обязательно. Приведенные здесь параллельные алгоритмы решения задач являются иллюстрационными, демонстрирующими применение и возможности функций MPI , а не универсальными, предназначенными для библиотек алгоритмов.
Рассматриваемые задачи распараллеливаются крупнозернистыми методами. Для представления алгоритмов используется SPMD — модель вычислений ( распараллеливание по данным). Однородное распределение данных по компьютерам – основа для хорошего баланса времени, затрачиваемого на вычисления, и времени, затрачиваемого на взаимодействия ветвей параллельной программы. При таком распределении преследуется цель: равенство объёмов распределяемых частей данных и соответствие нумерации распределяемых частей данных нумерации компьютеров в системе. Исходными данными рассматриваемых здесь алгоритмов являются матрицы, векторы и 2 D (двумерное) пространство вычислений. В этих алгоритмах применяются следующие способы однородного распределения данных: горизонтальными полосами, вертикальными полосами и циклическими горизонтальными полосами. При распределении горизонтальными полосами матрица, вектор или 2 D пространство «разрезается» на полосы по строкам (далее слово «разрезанная» будем писать без кавычек и матрицу, вектор или 2 D пространство обозначать для краткости словом — данные). Пусть M – количество строк матрицы, количество элементов вектора или количество строк узлов 2 D пространства, P – количество виртуальных компьютеров в системе, С1 = М / Р – целая часть от деления, С2 = М % Р – дробная часть. Данные разрезаются на Р полос. Первые (Р–С2) полос имеют по С1 строки, а остальные С2 полосы имеют по С1+1 строки. Полосы данных распределяются по компьютерам следующим образом. Первая полоса помещается в компьютер с номером 0, вторая полоса – в компьютер 1, и т. д. Такое распределение полос по компьютерам учитывается в параллельном алгоритме. Распределение вертикальными полосами аналогично предыдущему, только в распределении участвуют столбцы матрицы или столбцы узлов 2 D пространства. И, наконец, распределение циклическими горизонтальными полосами. При таком распределении данные разрезаются на количество полос значительно большее, чем количество компьютеров. И чаще всего полоса состоит из одной строки. Первая полоса загружается в компьютер 0, вторая – в компьютер 1, и т.д., затем, Р-1-я полоса снова в компьютер 0, Р-я полоса в компьютер 1, и т.д.
Приведенные два алгоритма решения СЛАУ методом Гаусса показывают, что однородность распределения данных сама по себе еще недостаточна для эффективности алгоритма. Эффективность алгоритмов зависит еще и от способа распределения данных. Разный способ представления данных влечет, соответственно, и разную организацию алгоритмов, обрабатывающих эти данные.
2.1 Запуск параллельной программы
Под виртуальным компьютером понимается программно реализуемый компьютер. Виртуальный компьютер работает в режиме интерпретации его физическим процессором. В одном физическом компьютере, в общем случае, может находиться и работать одновременно виртуальных компьютеров — столько, сколько позволяет память физического компьютера. На системе МВС1000 в одном физическом компьютере создается только один виртуальный. Под виртуальной топологией здесь понимается программно реализуемая топология связей между виртуальными компьютерами на физической системе.
Создаваемая пользователем виртуальная среда позволяет обеспечивать хорошую переносимость параллельных программ, а значит и независимость от конкретных вычислительных систем. Для пользователя очень удобно решать свою задачу в рамках виртуальной среды, использовать столько компьютеров, сколько необходимо для решения его задачи и задавать такую топологию связей между компьютерами, какая необходима.
Запуск параллельной программы продемонстрируем на примере. Допустим, требуется решить задачу program.c . Алгоритм задачи распараллелен на N процессов, независимо выполняющихся и взаимодействующих друг с другом. Задана нужная для решения задачи топология связей между этими процессами: — top (например, двумерная решетка). Для решения этой задачи было бы оптимально иметь вычислительную систему из N компьютеров (Для МВС1000 должно быть N ), с той же структурой связей, что и top . Далее в каждый компьютер необходимо загрузить по одному исполняемому модулю, реализующему ветвь параллельной программы, и стартовать эти модули. Ветви параллельной программы могут реализовываться копиями одной и той же программы (для МВС1000), а могут реализовываться разными программами (в общем случае). Опции и подробности загрузки нужно смотреть в соответствующих инструкциях.
Программа предварительно компилируется:
mpicc [ ] -o program.exe program.c
В квадратных скобках стоят опции нужной оптимизации. Для разных программ, разных компьютеров в вычислительной системе, для одинаковых компьютеров, но с разными операционными системами, нужно осуществлять отдельную компиляцию.
Здесь рассматривается команда запуска параллельной программы на системе МВС1000. Предполагается, что ветви параллельной программы реализуются копиями одной и той же программы. Необходимое количество физических компьютеров и виртуальных компьютеров задаются пользователем в командной строке:
mpirun -np N program.exe
N = <1,2,3,…>— указывает количество виртуальных компьютеров, необходимых для решения рассматриваемой программы с именем — program.exe . По этой команде система MPI создает (в оперативной памяти системы из N физических компьютеров) N виртуальных компьютеров, объединенных виртуальными каналами связи со структурой полный граф. И этой группе виртуальных компьютеров присваивается стандартное системное имя MPI_COMM_WORLD . После чего пользовательская программа program.exe загружается в память каждого из созданных виртуальных компьютеров и стартует.
Отображение виртуальных компьютеров и структуры их связи на конкретную физическую систему осуществляется системой MPI автоматически, т.е. пользователю не нужно переделывать свою программу для разных физических систем (с другими компьютерами и другой архитектурой). (Рассматриваемая версия MPI не позволяет пользователю осуществлять это отображение, либо осуществлять пересылку виртуальных компьютеров в другие физические компьютеры, т.е. не позволяет перераспределять виртуальные компьютеры по физическим компьютерам).
2.2 Умножение матрицы на матрицу
Умножение матрицы на вектор и матрицы на матрицу являются базовыми макрооперациями для многих задач линейной алгебры, например итерационных методов решения систем линейных уравнений и т. п. Поэтому приведенные алгоритмы можно рассматривать как фрагменты в алгоритмах этих методов. В этой секции приведено три алгоритма умножения матрицы на матрицу. Разнообразие вариантов алгоритмов проистекает от разнообразия вычислительных систем и размеров задач. Рассматриваются и разные варианты загрузки данных в систему: загрузка данных через один компьютер; и загрузка данных непосредственно каждым компьютером с дисковой памяти. Если загрузка данных осуществляется через один компьютер, то данные считываются этим компьютером с дисковой памяти, разрезаются и части рассылаются по остальным компьютерам. Но данные могут быть подготовлены и заранее, т.е. заранее разрезаны по частям и каждая часть записана на диск в виде отдельного файла со своим именем; затем каждый компьютер непосредственно считывает с диска, предназначенный для него файл.
2.2.1 Алгоритм 1
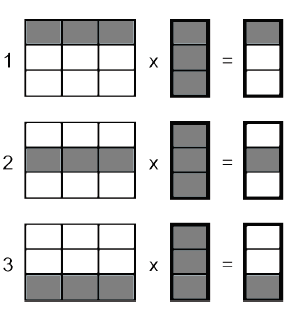
Заданы две исходные матрицы A и B . В ычисляется произведение C = А х B , где А — матрица n1 х n2 , и B — матрица n2 х n3 . Матрица результатов C имеет размер n1 х n3 . Исходные матрицы предварительно разрезаны на полосы, полосы записаны на дисковую память отдельными файлами со своими именами и доступны всем компьютерам. Матрица результатов возвращается в нулевой процесс.
Реализация алгоритма выполняется на кольце из p1 компьютеров. Матрицы разрезаны как показано на рисунке 2.1: матрица А разрезана на p1 горизонтальных полос, матрица B разрезана на p1 вертикальных полос, и матрица результата C разрезана на p1 полосы. Здесь предполагается, что в память каждого компьютера загружается и может находиться только одна полоса матрицы А и одна полоса матрицы B .
Решение систем линейных уравнений
Системы линейных уравнений возникают при решении ряда прикладных задач, описываемых дифференциальными, интегральными или системами нелинейных ( трансцендентных) уравнений . Они могут появляться также в задачах математического программирования, статистической обработки данных, аппроксимации функций, при дискретизации краевых дифференциальных задач методом конечных разностей или методом конечных элементов и др.
Матрицы коэффициентов систем линейных уравнений могут иметь различные структуру и свойства. Матрицы решаемых систем могут быть плотными, и их порядок может достигать несколько тысяч строк и столбцов. При решении многих задач могут появляться системы, обладающие симметричными положительно определенными ленточными матрицами с порядком в десятки тысяч и шириной ленты в несколько тысяч элементов. И, наконец, при рассмотрении большого ряда задач могут возникать системы линейных уравнений с разреженными матрицами с порядком в миллионы строк и столбцов.
8.1. Постановка задачи
Линейное уравнение с n неизвестными x0, x1, ѕ, xn-1 может быть определено при помощи выражения
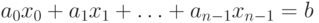 | ( 8.1) |
Множество из n линейных уравнений
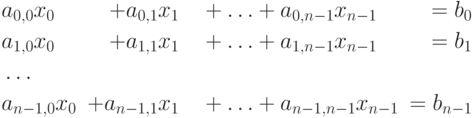 | ( 8.2) |
где A=(ai,j) есть вещественная матрица размера nxn , а векторы b и x состоят из n элементов.
Под задачей решения системы линейных уравнений для заданных матрицы А и вектора b обычно понимается нахождение значения вектора неизвестных x , при котором выполняются все уравнения системы.
8.2. Алгоритм Гаусса
Метод Гаусса – широко известный прямой алгоритм решения систем линейных уравнений , для которых матрицы коэффициентов являются плотными. Если система линейных уравнений невырожденна, то метод Гаусса гарантирует нахождение решения с погрешностью, определяемой точностью машинных вычислений. Основная идея метода состоит в приведении матрицы А посредством эквивалентных преобразований (не меняющих решение системы (8.2)) к треугольному виду, после чего значения искомых неизвестных могут быть получены непосредственно в явном виде.
В подразделе дается общая характеристика метода Гаусса, достаточная для начального понимания алгоритма и позволяющая рассмотреть возможные способы параллельных вычислений при решении систем линейных уравнений . Более полное изложение алгоритма со строгим обсуждением вопросов точности получаемых решений может быть получено, например, в работах [ [ 6 ] , [ 22 ] , [ 47 ] ] и др.
8.2.1. Последовательный алгоритм
Метод Гаусса основывается на возможности выполнения преобразований линейных уравнений , которые не меняют при этом решения рассматриваемой системы (такие преобразования носят наименование эквивалентных ). К числу таких преобразований относятся:
- умножение любого из уравнений на ненулевую константу;
- перестановка уравнений;
- прибавление к уравнению любого другого уравнения системы.
Метод Гаусса включает последовательное выполнение двух этапов. На первом этапе – прямой ход метода Гаусса – исходная система линейных уравнений при помощи последовательного исключения неизвестных приводится к верхнему треугольному виду
где матрица коэффициентов получаемой системы имеет вид
На обратном ходе метода Гаусса (второй этап алгоритма) осуществляется определение значений неизвестных. Из последнего уравнения преобразованной системы может быть вычислено значение переменной xn-1 , после этого из предпоследнего уравнения становится возможным определение переменной xn-2 и т.д.
8.2.1.1. Прямой ход алгоритма Гаусса
Прямой ход метода Гаусса состоит в последовательном исключении неизвестных в уравнениях решаемой системы линейных уравнений . На итерации i, 0 , метода производится исключение неизвестной i для всех уравнений с номерами k , большими i (т.е. i ). Для этого из этих уравнений осуществляется вычитание строки i , умноженной на константу ( aki/aii ), с тем чтобы результирующий коэффициент при неизвестной xi в строках оказался нулевым – все необходимые вычисления могут быть определены при помощи соотношений:
Поясним выполнение прямого хода метода Гаусса на примере системы линейных уравнений вида:
На первой итерации производится исключение неизвестной x0 из второй и третьей строки. Для этого из этих строк нужно вычесть первую строку, умноженную соответственно на 2 и 1. После этих преобразований система уравнений принимает вид:
В результате остается выполнить последнюю итерацию и исключить неизвестную x1 из третьего уравнения. Для этого необходимо вычесть вторую строку, и в окончательной форме система имеет следующий вид:
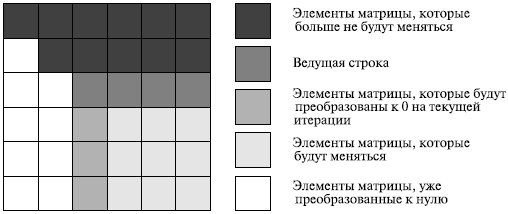
На рис. 8.1 представлена общая схема состояния данных на i -й итерации прямого хода алгоритма Гаусса . Все коэффициенты при неизвестных, расположенные ниже главной диагонали и левее столбца i , уже являются нулевыми. На i -й итерации прямого хода метода Гаусса осуществляется обнуление коэффициентов столбца i , расположенных ниже главной диагонали, путем вычитания строки i , умноженной на нужную ненулевую константу. После проведения (n-1) подобной итерации матрица, определяющая систему линейных уравнений , становится приведенной к верхнему треугольному виду.
При выполнении прямого хода метода Гаусса строка, которая используется для исключения неизвестных, носит наименование ведущей, а диагональный элемент ведущей строки называется ведущим элементом. Как можно заметить, выполнение вычислений является возможным только, если ведущий элемент имеет ненулевое значение. Более того, если ведущий элемент ai,i имеет малое значение, то деление и умножение строк на этот элемент может приводить к накоплению вычислительной погрешности и вычислительной неустойчивости алгоритма.
Возможный способ избежать подобной проблемы может состоять в следующем: при выполнении каждой очередной итерации прямого хода метода Гаусса следует определить коэффициент с максимальным значением по абсолютной величине в столбце, соответствующем исключаемой неизвестной, т.е.
Вычислительная сложность прямого хода алгоритма Гаусса с выбором ведущей строки имеет порядок O(n 3 ) .
8.2.1.2. Обратный ход алгоритма Гаусса
После приведения матрицы коэффициентов к верхнему треугольному виду становится возможным определение значений неизвестных. Из последнего уравнения преобразованной системы может быть вычислено значение переменной xn-1 , после этого из предпоследнего уравнения становится возможным определение переменной xn-2 и т.д. В общем виде выполняемые вычисления при обратном ходе метода Гаусса могут быть представлены при помощи соотношений:
Поясним, как и ранее, выполнение обратного хода метода Гаусса на примере рассмотренной в п. 8.2.1.1 системы линейных уравнений
Из последнего уравнения системы можно определить, что неизвестная x2 имеет значение 3 . В результате становится возможным разрешение второго уравнения и определение значение неизвестной x1=13 , т.е.
На последней итерации обратного хода метода Гаусса определяется значение неизвестной x0 , равное -44 .
С учетом последующего параллельного выполнения можно отметить, что вычисление получаемых значений неизвестных может выполняться сразу во всех уравнениях системы (и эти действия могут выполняться в уравнениях одновременно и независимо друг от друга). Так, в рассматриваемом примере после определения значения неизвестной x2 система уравнений может быть приведена к виду
Вычислительная сложность обратного хода алгоритма Гаусса составляет O(n 2 ) .
Участник:Макарова Алёна/Итерационный метод решения системы линейных алгебраических уравнений GMRES (обобщенный метод минимальных невязок)
| Обобщенный метод минимальных невязок | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(nm^2)[/math] |
| Объём входных данных | [math]n(n + 1)[/math] |
| Объём выходных данных | [math]n[/math] |
Содержание
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Метод минимальных невязок представляет собой итерационный метод для численного решения несимметричной системы линейных уравнений. Метод приближает решение вектором в подпространстве Крылова с минимальной невязкой. Чтобы найти этот вектор используется итерация Арнольди.
Впервые метод минимальных невязок был описан в книге Марчука и Кузнецова «Итерационные методы и квадратичные функционалы» [1] и представлял собой геометрическую реализацию метода минимальных невязок.
Алгебраическая реализация метода минимальных невязок была предложена Саадом и Шульцем в 1986 году [2] . С их подачи за методом закрепилась аббревиатура GMRES (обобщенный метод минимальных невязок).
1.2 Математическое описание алгоритма
Для решения системы [math]Ax = b[/math] с невырожденной матрицей [math]A[/math] , выбирается начальное приближение [math]x_0[/math] , затем решается редуцированная система [math]Au = r_0[/math] , где [math]r_0 = b — Ax_0, x = x_0 + u[/math] . Подпространства Крылова строятся для редуцированной системы (в предположении, что [math]r_0 \neq 0[/math] ).
Пусть [math]x_i = x_0 + y[/math] , где [math] y \in \mathcal
[math] r_i \perp A\mathcal
Таким образом, для реализации [math]i[/math] -го шага требуется опустить перпендикуляр из вектора [math]r_0[/math] на подпространство [math]A\mathcal
1.2.1 Геометрическая реализация
Геометрическая реализация метода минимальных невязок заключается в построении последовательности векторов [math]q_1, q_2. [/math] таким образом, что [math]q_1, q_2. q_i[/math] дают базис в подпространстве Крылова [math]\mathcal
[math] q_
Его можно получить с помощью процесса ортогонализации, применённого к вектору [math]p = Aq[/math] , где [math]q = Aq_i[/math] . В геометрической реализации необходимо хранить две системы векторов: [math]q_1, . q_i[/math] и [math]p_1, . p_i[/math] .
1.2.2 Алгебраическая реализация
Алгебраическая реализация метода минимальных невязок использует лишь одну систему векторов, образующих ортогональные базисы в подпространствах [math]\mathcal
[math]q_1 = r_0/||r_0||_2[/math] . Чтобы получить ортонормированный базис [math]q_1, . q_
[math] AQ_i = Q_
где [math]H_i[/math] — верхняя хессенбергова матрица порядка [math]i[/math] .
Далее рассмотрим [math]QR[/math] -разложение прямоугольной матрицы [math]\hat
[math] \hat
Тогда минимум невязки [math]||r_0 — AQ_iy||_2[/math] по всем [math]y[/math] будет достигаться в том случае, если [math]y = y_i[/math] удовлетворяет уравнению
[math] R_iy_i = z_i \equiv ||r_0||_2U^T_ie_1, e_1 = \begin
Матрица [math]R_i[/math] невырожденная, следовательно,
[math] x_i = x_0 + Q_iy_i = x_0 + Q_iR_i^<-1>z_i [/math] .
1.2.3 Сходимость метода
Метод минимизации невязок на подпространствах Крылова за конечное число итераций приводит к точному решению и по этой причине является прямым методом. Но чаще его рассматривают как итерационный метод — с типичными для итерационных методов оценками сходимости. Идея заключается в том, что спустя некоторое небольшое (относительно размера матрицы — [math]m[/math] ) количество итераций [math]n[/math] , полученное приближение уже является хорошей оценкой ответа.
Но об этом не верно говорить в общем. Согласно теореме (Greenbaum, Pták and Strakoš) [4] , для каждой монотонной последовательности [math] a_1. a_
На практике для матрицы порядка [math]m[/math] число шагов может оказаться равным [math]m[/math] , а норма невязки может оставаться равной норме начальной невязки на всех шагах, кроме последнего.
[math] \begin
Если [math] x_0 = 0 [/math] , то [math] r_0 = b[/math] . Подпространства Крылова получаются такие:
[math] \mathcal
Точное решение системы имеет вид [math]x = e_1[/math] , а на итерациях получаются следующие векторы:
[math] x_0 = x_1 = . = x_
Для получения оценок требуются дополнительные предположения относительно матрицы коэффициентов.
1.2.3.1 Сходимость для положительно определенной матрицы
Если матрица [math]A[/math] положительно определена, то
где [math]\lambda_<\mathrm
1.2.3.2 Сходимость для симметричной матрицы
Если матрица [math]A[/math] является симметричной и положительно определена, тогда
где [math]\kappa_2(A)[/math] число обусловленности матрицы [math]A[/math] в Евклидовой норме.
Если не требовать положительной определённости
где [math]P_n[/math] обозначает множество полиномов степени не выше [math]n[/math] и [math]p(0) = 1[/math] , матрица [math]V[/math] появляется из спектрального разложения матрицы [math]A[/math] и [math]\sigma(A)[/math] — спектр матрицы [math]A[/math] . Грубо говоря, это означает, что быстрая сходимость имеет место, когда собственные значения матрицы [math]A[/math] невелики и [math]A[/math] не сильно отклоняется от нормальной матрицы. [6]
Все эти неравенства связаны с невязкой вместо фактической ошибки, т.е. расстоянием между текущей итерацией и точным решением.
1.3 Вычислительное ядро алгоритма
Самой трудоёмкой процедурой в методе является [math]QR[/math] -разложение [math]\hat
1.4 Макроструктура алгоритма
Алгоритм начинается с выбора начального приближения [math]x_0[/math] . Далее для [math]i = 1,2 ..[/math]
1. Вычисляем матрицу [math]\hat
Алгоритм завершается, когда норма вектора невязки становится достаточно малой. При большом числе итераций вычислительные затраты и требуемая для хранения векторов [math]p_i[/math] память могу оказаться чрезмерно большими. В таких случаях применяют алгоритм с перезапусками (restart): задают максимальную допустимую размерность [math]K[/math] пространств Крылова [math]\mathcal
1.5 Схема реализации последовательного алгоритма
- Инициализация начальных значений
1. Выбрать начальное приближение [math]x_0[/math] и точность решения [math]\epsilon[/math] .
2. Для [math] k = 1, 2, .. [/math]
3. [math]r_0 = b — Ax_0[/math] , [math]\beta = ||r_0||[/math] , [math]q_1 = r_0/\beta[/math] .
4. Цикл по [math] j = 1, 2, .. k [/math] .
5. Для каждого [math] i = 1, 2, .. j [/math] вычислим:
[math]h_
6. Построим вектор: [math]z_
7. Вычислим его норму [math]h_
8. Если [math]h_
9. Построим очередной вектор базиса [math]q_
10. Конец цикла по [math]j[/math] .
11. Процесс требует хранения всех предыдущих элементов базиса: [math]q_1, .. q_k[/math] . Будем хранить их в виде матриц [math]Q_k[/math] .
- Задача наименьших квадратов
12. Чтобы вычислить [math]x_k = x_0 + Q_ky_k[/math] , решаем задачу: [math] y_k = argmin ||r_0 — AP_ky_k||_2[/math] .
- Проверка достижения требуемой точности приближения
13. Если [math]||b — Ax_k|| \lt \epsilon[/math] , где [math]x_k = x_0 + Q_ky_k[/math] перейти к п.15
14. [math]x_0 = x_k[/math] , перейти к п.2
15. [math]x^* = x_k[/math]
1.6 Последовательная сложность алгоритма
Будем предполагать, что матрица решаемой СЛАУ является разреженной. Количество внедиагональных ненулевых элементов в которой равно [math]k[/math] .
Тогда при [math] m \lt \lt n [/math] можно говорить, что один GMRES-цикл имеет сложность [math]\mathcal
Требования по памяти с учетом [math]1 \lt m \lt \lt n[/math] и [math]k \lt \lt n[/math] составляют [math]\mathcal
1.7 Информационный граф
Основным ресурсом параллелизма будут являться умножение матрицы на вектор [8] и вычисление скалярных произведений [9] . Представим информационные графы для данных алгоритмов:
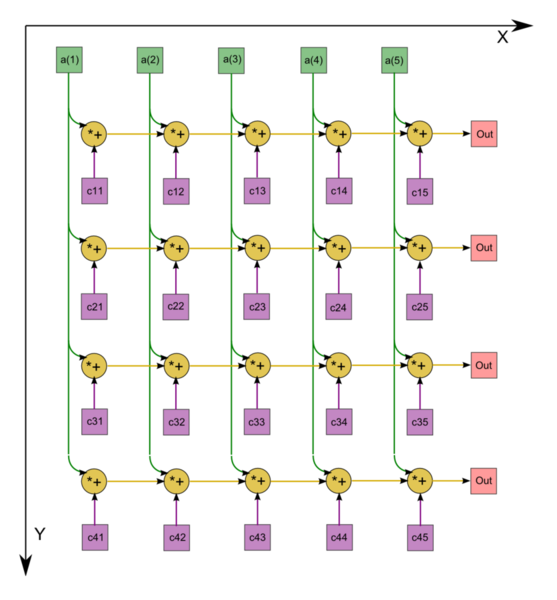
Рисунок 1. Граф последовательного умножения плотной матрицы на вектор с отображением входных и выходных данных
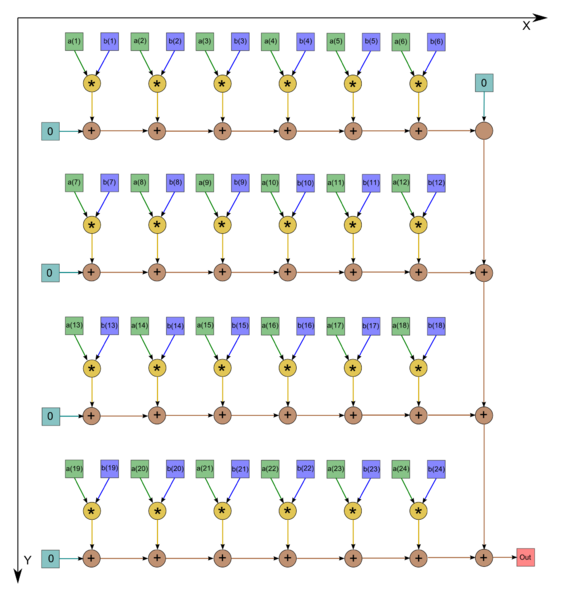
Рисунок 2. Последовательно-параллельное вычисление скалярного произведения
Граф алгоритма умножения плотной матрицы на вектор состоит из одной группы вершин, расположенной в целочисленных узлах двумерной области, соответствующая ей операция [math]a+bc[/math] .
Описанный граф выполнен для случая [math]m = 4 , n = 5[/math] . Изображена подача только входных данных из вектора [math]x[/math] , подача элементов матрицы [math]A[/math] , идущая во все вершины, на рисунке не представлена.
Для алгоритма нахождения скалярного произведения двух векторов граф состоит из двух групп вершин, им соответсвуют операции [math]a*b[/math] и [math] c+d[/math] . Данный граф изображен для случая [math]n = 24[/math] .
1.8 Ресурс параллелизма алгоритма
В вычислительной схеме присутствуют два интенсивных в вычислительном плане этапа:
1. Умножение матрицы СЛАУ на вектор (для нахождения невязок).
Для нахождения матрично-векторных произведений, при вычислении невязок, матрица должна быть подвергнута декомпозиции на строчные блоки.
2. Нахождение скалярных произведений векторов (при построении ортонормального базиса подпространства Крылова).
Для наиболее эффективного вычисления скалярных проихведений и линейных комбинаций векоров базиса каждый из векторов [math]p_i[/math] должен быть разбит на блоки равного размера по числу процессоров.
Кроме того, на хранение векторов базиса приходится бОльшая часть затрат памяти.
1.9 Входные и выходные данные алгоритма
Входные данные: Обязательные параметры:
[math]A[/math] — квадратная матрица (n x n). [math]b[/math] — вектор правой части (n x 1).
[math]x_0[/math] — начальное приближение (может не передаваться и быть всегда нулевым). [math]\epsilon[/math] — погрешность (может не передаваться и быть заданным по умолчанию, обычно равна 1e-6). Максимальное число итераций.
Выходные данные: [math]x^*[/math] — решение системы [math]Ax = b[/math]
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
Реализация GMRES с преобуславливанием на python, доступная в пакете scipy (scipy.sparse.linal) [10] .
2.2 Локальность данных и вычислений
2.2.1 Локальность реализации алгоритма
2.2.2 Структура обращений в память и качественная оценка локальности
2.2.3 Количественная оценка локальности
2.3 Возможные способы и особенности параллельной реализации алгоритма
Возможный способ реализации приведен в работе Буренкова С.А. [11] . А также рассмотрены особенности параллельной реализации алгоритма.
2.3.1 Распределение данных
При выполнении параллельного алгоритма решения систем линейных алгебраических уравнений необходимо распределить входные данные наиболее рациональным способом. Матрица коэффициентов разбивается на непрерывные горизонтальные полосы. Распределение вектора правой части и начального приближения выполнено по принципу дублирования, т.е. все элементы векторов скопированы на все процессоры. Для рассматриваемой задачи решения СЛАУ такой подход распределения допустим, т.к. векторы содержат столько же элементов, сколько и одна строка или один столбец матрицы коэффициентов. Если процессор хранит строку матрицы и одиночные элементы векторов правой части и начального приближения, то общее число сохраняемых элементов имеет порядок . Если же процессор хранит строку матрицы и все элементы векторов, то общее число сохраняемых элементов также порядка . Таким образом, при дублировании и при разделении векторов требования к объему памяти из одного класса сложности.
2.3.2 Выполнение параллельных операций
Рассмотрим операции, которые выполняются неоднократно в процессе выполнения алгоритма: умножение матрицы на вектор, произведение векторов, расчет нормы вектора, линейной комбинации векторов. Эти подзадачи можно разделить на 2 группы: операции между матрицей и вектором (например, умножение матрицы на вектор) и операции между двумя векторами (например, скалярное умножение, взвешенная сумма векторов и пр.). Подзадачи умножения константы на вектор и определение нормы вектора будем относить ко второй группе, так как их трудоемкость одного порядка.
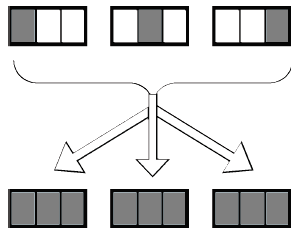
Особенности выполнения операций между матрицей и вектором определены способом распределения входных данных. На рис. 2 схематично изображен процесс параллельного умножения матрицы на вектор на трех процессорах.
Заштрихованные участки соответствуют данным, расположенным в памяти процессора исполнителя. Каждый исполнитель получает свою часть результата выполнения операции.
По схожему принципу организовано параллельное выполнение операций между двумя векторами. Несмотря на то, что каждому процессу доступна полная информация о векторах, вычисления производятся лишь над участком, соответствующим процессу-исполнителю. На рис. 3 изображен пример параллельного выполнения операций между двумя векторами.
Таким образом, параллельное выполнение любой из выделенных подзадач привело к распределению вычислительной нагрузки между всеми исполнителями.
2.3.3 Объединение результатов расчетов
Результатом выполнения рассматриваемых операций является, чаще всего, вектор, части которого расположены на участвовавших в вычислениях процессорах. Для объединения результатов расчета и получения полного вектора на каждом процессоре вычислительной системы необходимо выполнить операцию сбора данных. В качестве обменных взаимодействий в модели с распределённой памятью могут выступать операции массовых коммуникационных обменов. С их помощью каждый процессор передаст свой вычисленный элемент вектора всем остальным процессорам (см. рис. 4).
2.4 Масштабируемость алгоритма и его реализации
2.4.1 Масштабируемость алгоритма
2.4.2 Масштабируемость реализации алгоритма
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Алгоритм GMRES достаточно популярен и его реализацию можно найти во многих пакетах прикладных программ.
Список пакетов, в которых присутствует реализация метода минимизации обобщенной невязки:
1.ATLAS (Automatically Tuned Linear Algebra Software) – оптимизированная библиотека, включающая реализацию процедур BLAS и часть функциональности LAPACK; 2.AZTEC – библиотека параллельных подпрограмм для решения больших систем линейных алгебраических уравнений с разреженными матрицами; 3.BLAS (Basic Linear Algebra Subprograms) – библиотека высококачественных процедур, «строительными блоками» для которых являются вектора, матрицы или их части. Уровень 1 BLAS используется для выполнения операций вектор-вектор, уровень 2 :BLAS – для выполнения матрично-векторных операций, наконец, уровень 3 BLAS – для выполнения матрично-матричных операций. Поскольку программы BLAS являются эффективными, переносимыми и легко доступными, они используются как базовые компоненты для развития высококачественного программного обеспечения для задач линейной алгебры. Так были созданы широко известные пакеты LINPACK, EISPACK, которые затем были перекрыты пакетом LAPACK, получившим большое распространение. Перечисленные пакеты разработаны на языке Fortran; 4.BLACS (Basic Linear Algebra Communication Subprograms) – набор базовых коммуникационных процедур линейной алгебры, созданных для линейной алгебры. Вычислительная модель состоит из одномерной или двумерной решетки процессов, где каждый процесссодержит часть матрицы или вектора. BLACS используется как коммуникационный слой проекта ScaLAPACK, который переносит библиотеку LAPACK на машины с распределенной памятью; 5.BlockSolve95 – параллельная библиотека для решения разреженных систем линейных уравнений; 6.BPKIT2 – пакет блочных способов предобусловливания, ориентированных на разреженные матрицы; 7.CAPSS – пакет для параллельного решения разреженных линейных систем; 8.CXML (The Compaq Extended Math Library) – расширенная математическая библиотека, включающая в себя часть функциональности BLAS, LAPACK, Direct Sparse Solvers и Iterative-solvers; 9.Direct Sparse Solvers – пакет программ для решения разреженных систем прямыми методами; 10.EISPACK (Eigensystem Package) – пакет программ решения алгебраической проблемы собственных значений; 11.Expokit – пакет программ для решения не больших СЛАУ с плотной матрицей и больших разреженных систем; 12.ILUPACK – библиотке, содержащая способы предобусловливания, ориентированная на разреженные СЛАУ. Пакет включает реализацию процедур BLAS, SPARSEKIT. Реализована на языке С и Fortran; 13.IML++ (Iterative Methods Library) – библиотека итерационных методов решения разреженных СЛАУ, позволяющая использовать несколько простых способов предобусловливания. Пакет включает часть BLAS и MV; 14.Intel MKL (Intel Math Kernel Library) включает несколько стандартных библиотек для высокопроизводительных системах (BLAS, LAPACK и FFTPACK – подпрограммы быстрого преобразования Фурье); 15.IOMDRV – пакет подпрограмм для решения симметричных и несимметричных линейных систем методами крыловских подпространств; 16.Iterative-solvers – пакет подпрограмм решения разреженных систем итерационными методами; 17.ITL (Iterative Template Library) – библиотека программ итерационных методов и способов предобусловливания, являющаяся составной частью MTL. 18.ITPACK (Iterative Package) – пакет программ для решения разреженных систем итерационными методами; 19.ITSOL (The New Sparskit Preconditionning Module) – пакет, содержащий способы предобусловливания, ориентированные на разреженные матрицы. Является составной частью пакета SPARSKIT; 20.JAMA/C++ – библиотека для решения СЛАУ прямыми методами; 21.LAPACK (Linear Algebra Package) – набор реализаций «продвинутых» методов линейной алгебры. LAPACK содержит процедуры для решения систем линейных уравнений, задач нахождения собственных значений и факторизации матриц. Обрабатываются заполненные и ленточные матрицы, но не разреженные матрицы общего вида. Во всех случаях можно обрабатывать действительные и комплексные матрицы с одиночной и удвоенной точностью. Процедуры LAPACK построены таким образом, чтобы как можно больше вычислений выполнялось с помощью обращений к BLAS с использованием всех его трех уровней. Вследствие крупнозернистости операций уровня 3 BLAS, их использование обеспечивает высокую эффективность на многих высокопроизводительных компьютерах, в частности, если производителем создана специализированная реализация. ScaLAPACK является успешным результатом переноса пакета LAPACK на системы с передачей сообщений. Но в таких системах необходимы процедуры, обеспечивающие обмен данными между взаимодействующими процессами. Для этого в ScaLAPACK используется библиотека BLACS; 22.Laspack – пакет программ для решения разреженных систем итерационными методами; 23.LGSOLV – библиотека для решения СЛАУ прямыми методами; 24.LINPACK (Linear Package) – пакет программ решения систем линейных алгебраических уравнений и линейной задачи наименьших квадратов прямыми методами; 25.LinPar – пакет предназначенный для решения плохообусловленных СЛАУ, включая прямоугольные. Если для решения задачи необходимо предобусловливание СЛАУ, то оно выполняется отдельно и методы применяются к уже предобусловленной системе. Соответственно, по окончании процесса решения найденный вектор должен быть пересчитан согласно выполненному предобусловливанию. В схемы методов эти процедуры не включаются; 26.MET (Matrix Expression Templates) – реализованная на языке C++ программа для инженеров и научных работников; 27.MINOS – пакет подпрограмм решения больших разреженных задач линейного и нелинейного программирования; 28.MTL (The Matrix Template Library) – реализованная на языке C++ библиотека базовых операций линейной алгебры, позволяющая решать СЛАУ с разреженными матрицами итерационными методами с предобусловлмванием, за счет включенного пакета ITL; 29.MV++ – небольшая библиотека, содержащая базовые операции линейной алгебры. Данный пакет часто является составной частью более крупных и высокопроизводительных библиотек; 30.ParPre – пакет параллельных версий способов предобусловливания, ориентированных на разреженные матрицы, являющийся составной частью PETs; 31.Parallel Algorithms Project – пакет параллельных версий итерационных методов Крыловского типа для решения разреженных систем; 32.PASVA – пакет подпрограмм решения разреженных систем с блочно-двухдиагональной структурой; 33.PBLAS – Параллельные версии базовых процедур линейной алгебры (BLAS) ; 34.PCGPAK (Preconditioned Conjugate Gradient PAcKage) – пакет программ для решения симметричных и несимметричных разреженных линейных систем методом сопряженных градиентов; 35.PIM (The Parallel Iterative Methods) – набор процедур на Фортран-77, реализующих параллельные версии различных итеративных методов решения разреженных систем линейных уравнений; 36.PSparselib (A Portable Library of Parallel Sparse Iterative Solvers) – библиотека параллельных итерационных методов для разреженных линейных систем; 37.PSPASES (Parallel Sparse Symmetric Direct Solver) – библиотека параллельных версий прямых методов для решения симметричных линейных систем; 38.RALAPACK – пакет подпрограмм для различных операций с разреженными матрицами; 39.ScaLAPACK (Scalable LAPACK) – параллельная версия LAPACK. Широкий набор подпрограмм для решения стандартных задач линейной алгебры; 40.SIRSM – пакет подпрограмм для решения разреженных несимметричных линейных систем; 41.Software Iterative Methods: GMRESR and BiCGstab(ell) – пакет прогамм решения больших разреженных систем с несимметричной матрицей; 42.SPAI (Sparse Approximate Inverse Preconditioner) – пакет способов предобусловливания, ориентированных на разреженные матрицы; 43.SPARKS – пакет подпрограмм для решения разреженных линейных систем в полунеявных методах Рунге-Кутта численного интегрирования систем обыкновенных дифференциальных уравнений; 44.SparseLib++ – библиотка, реализованная на языке C++, позволяющая решать разреженные СЛАУ итерационными методами с предобусловливанием. Включает часть процедур BLAS и IML; 45.SPARSKIT – мощный пакет для решения разреженных СЛАУ итерационными методами с предобусловливанием. Библиотека реализованна на языке Fortran; 46.SPARSPAK (Sparsee Iinear Equations Package) – пакет программ решения разреженных систем линейных алгебраических уравнений с симметричными положительно определенными матрицами; 47.SPLIB – библиотека, позволяющая решать СЛАУ с разреженной матрицей итерационными методами с предобусловливанием, реализованная на языке Fortran; 48.SPLP (Sparse Linear Programming Subprogram) – пакет программ решения задач линейного программирования; 49.SPOOLES – библиотека для решения СЛАУ с разреженной матрицей прямыми методами; 50.SSLES – пакет подпрограмм для решения разреженных несимметричных линейных систем; 51.TCHLIB – пакет подпрограмм для решения симметричных и несимметричных линейных систем методом Чебышева; 52.TNT (Template Numerical Toolkit) – библиотека базовых операций линейной алгебры, ориентированная на разреженные матрицы. Библиотека разработана на языке Fortran; 53.WSMP (Watson Sparse Matrix Package) – пакет программ решения разреженных систем линейных алгебраических уравнений; 54.XMP – пакет подпрограмм для решения задач линейного программирования; 55.YI2M – комплекс программ решения разреженных систем;
http://intuit.ru/studies/courses/1156/190/lecture/4956
http://algorithms.parallel.ru/ru/%D0%A3%D1%87%D0%B0%D1%81%D1%82%D0%BD%D0%B8%D0%BA:%D0%9C%D0%B0%D0%BA%D0%B0%D1%80%D0%BE%D0%B2%D0%B0_%D0%90%D0%BB%D1%91%D0%BD%D0%B0/%D0%98%D1%82%D0%B5%D1%80%D0%B0%D1%86%D0%B8%D0%BE%D0%BD%D0%BD%D1%8B%D0%B9_%D0%BC%D0%B5%D1%82%D0%BE%D0%B4_%D1%80%D0%B5%D1%88%D0%B5%D0%BD%D0%B8%D1%8F_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D1%8B_%D0%BB%D0%B8%D0%BD%D0%B5%D0%B9%D0%BD%D1%8B%D1%85_%D0%B0%D0%BB%D0%B3%D0%B5%D0%B1%D1%80%D0%B0%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D1%85_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B9_GMRES_(%D0%BE%D0%B1%D0%BE%D0%B1%D1%89%D0%B5%D0%BD%D0%BD%D1%8B%D0%B9_%D0%BC%D0%B5%D1%82%D0%BE%D0%B4_%D0%BC%D0%B8%D0%BD%D0%B8%D0%BC%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D1%85_%D0%BD%D0%B5%D0%B2%D1%8F%D0%B7%D0%BE%D0%BA)