Системы материальных точек как уравнение движения

Уравнение движения материальной точки

Движение материальной точки в пространстве – это изменение ее положения относительно других тел с течением времени.

Имеет смысл говорить только о движении в некоторой системе отсчета.

Система отсчета. Системы координат

Точки, располагаемые в пустом пространстве, не различаются. Поэтому о точке рассуждают при условии нахождения в ней материальной точки. Определить ее положение можно при помощи измерений в системе координат, где и проводится нахождение пространственных координат. Если рассматривать в виде примера поверхность Земли, то следует учитывать широту и долготу располагаемой точки.

В теории используется декартова прямоугольная система координат, где определение точки возможно при наличии радиус-вектора r и трех проекций x , y , z – ее координат. Могут быть применены другие:

• сферическая система с положением точек и ее радиус-вектором, определенных координатами r , υ , φ ;
• цилиндрическая система с координатами p , z , α ;
• на полярной плоскости с параметрами r , φ .

В теории зачастую не принимают во внимание реальную систему отсчета, а сохраняют только ту, которая представляет собой ее математическую модель, применяемую во время практических измерений.

Кинематическое уравнение движения материальной точки

Любая система отсчета или координат предполагает определение координат материальной точки в любой момент времени.

При условии положения и определения материальной точки в данной системе отсчета считается, что ее движение задано или описано.

Это возможно при использовании кинематического уравнения движения:

Аналитически положение точки определяется совокупностью трех независимых между собой чисел. Иначе говоря, свободная точка имеет три степени свободы движения.

Ее перемещение по уравнению ( 1 ) определено, если имеется указанное положение в любой момент времени t . Для этого следует задавать декартовы координаты точки в качестве однозначных и непрерывных функций времени:

x ( t ) = x , y ( t ) = y , z ( t ) = z ( 2 ) .

Прямоугольные декартовы координаты x , y , z — это проекции радиус-вектора r ¯ , проведенного из начала координат. Очевидно, что длину и направление r ¯ можно найти из соотношений, где a , β , γ являются образованными радиус-вектором углами с координатными осями.

Равенства ( 2 ) считают кинематическими уравнениями движения материальной точки в декартовых координатах.

Они могут быть записаны в другой системе координат, которая связана с декартовой взаимно однозначным преобразованием. Если движение точки происходит в плоскости О х у , тогда применимы полярные координаты r , φ , относящиеся к декартовым преобразованиям. Данный случай подразумевает использование уравнения движения точки следующего вида:

r = r ( t ) , φ = φ ( t ) ( 3 ) .

Кинематическое уравнение движения точки в криволинейных координатах q 1 , q 2 , q 3 , связанных с декартовыми преобразованиями вида x = x ( q 1 , q 2 , q 3 ) , y = y ( q 1 , q 2 , q 3 ) , z = z ( q 1 , q 2 , q 3 ) ( 4 ) , записывается как

q 1 = q 1 ( t ) , q 2 = q 2 ( t ) , q 3 = q 3 ( t ) ( 5 ) .

Кривая радиус-вектора, описываемая концом вектора r при движении точки, совпадает с ее траекторией. Параметрическое уравнение траектории с t представлено кинематическими уравнениями ( 2 ) , ( 5 ) . Чтобы получить координатное уравнение траектории следует исключить время из кинематических уравнений.

Определение движения точки возможно с помощью задания траектории и мгновенного положения точки на ней. Ее положение на кривой определяется с помощью указания только одной величины: расстояния вдоль кривой от некоторой начальной точки с положительным направлением:

Это и есть уравнение движения точки по траектории. Способ его задания относят к естественному или траекторному.

Понятия координатного и естественного способа задания движения точки физически эквивалентны. С математической стороны это рассматривают как возможность применения разных методов, исходя из случая математической задачи.

Задание такого закона возможно аналитическим, графическим путем или с использованием таблицы, последние два из которых зачастую рассматривают в виде графиков и расписаний движений поездов.

Дано уравнение движения материальной точки x = 0 , 4 t 2 . Произвести запись формулы зависимости υ x ( t ) , построить график зависимости скорости от времени. На графике отметить площадь, численно равную пути, пройденному точкой за 4 секунды, произвести вычисление.

Дано: x = 0 , 4 t 2 , t = 4 c

Найти: υ x ( t ) , S — ?

Решение

При решении необходимо учитывать зависимость скорости от времени:

υ x = υ 0 x + a x t .

Зависимость координаты от времени и сравнение уравнения с заданным принимает вид:

x = x 0 + υ 0 x t + a x t 2 2 , x = 0 , 4 t 2 .

Очевидно, что x 0 = 0 , υ 0 x = 0 , a x = 0 , 8 м / с 2 .

После подстановки данных в уравнение:

Определим точки, изобразим график:

υ x = 0 , t = 0 , υ x = 4 , t = 5

Путь, по которому двигалось тело, равняется площади фигуры, ограниченной графиком, и находится с помощью формулы:

Система материальных точек. Вывод уравнения движения системы материальных точек на примере двух жестко связанных тел(хз)

Системой материальных точек называется такая их совокупность, в которой положение и движение каждой точки зависит от положения и движения всех точек данной системы. Часто систему материальных точек называют механической системой.

Центр масс системы материальных точек. Определение радиус-вектора центра масс. Свойства центра масс. Скорость центра масс. Вывод уравнения движения центра масс. Закон сохранения координаты центра масс системы материальных точек.

тром масс (или центром инерции)

системы материальных точек называет-

ся воображаемая точка С, положение

которой характеризует распределение

массы этой системы. Ее радиус-вектор

Центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается неподвижным.

Скорсть центра масс

Для непрерывного распределения массы с плотностью r . Если силы тяжести, приложенные к каждой частице системы, направлены в одну сторону, то центр масс совпадает с центром тяжести. Но если не параллельны, то центр масс и центр тяжести не совпадают.
Взяв производную по времени от , получим:

т.е. полный импульс системы равен произведению ее массы на скорость центра масс.

Подставляя это выражение в закон изменения полного импульса, находим:

Центр масс системы движется как частица, в которой сосредоточена вся масса системы и к которой приложена результирующая внешних сил.

При поступательном движении все точки твердого тела движутся так же, как и центр масс (по таким же траекториям), поэтому для описания поступательного движения достаточно записать и решить уравнение движения центра масс.

Так как , то центр масс замкнутой системыдолжен сохранять состояние покоя или равномерного прямолинейного движения, т.е. =const. Но при этом вся система может вращаться, разлетаться, взрываться и т.п. в результате действия внутренних сил.

Rс(t1) = Rc(t2) закон сохранения координаты центра масс

Работа потенциальных (консервативных) силы на примере силы тяжести. Определение потенциальных (консервативных) силовых полей. Введение понятия потенциальной энергии через работу силы. Связь силы и потенциальной энергии

Потенциальная сила — сила, работа к-рой зависит только от начального и конечного положения точки её приложения и не зависит ни от вида траектории, ни от закона движения этой точки. Консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0.
Потенциальное (консервативное) силовое поле:Потенциальным называется поле, работа которого при переходе из одной точки поля в другую не зависит от формы траектории. Потенциальными являются поле силы тяжести и электростатическое поле.
Введения понятия потенц. Энергии через работу сил — Потенциальная энергия — скалярная физическая величина, характеризует запас энергии некоего тела (или материальной точки), находящегося в потенциальном силовом поле, который идет на приобретение (изменение) кинетической энергии тела за счет работы сил поля.
Связь силы и потенциальной энергии — Каждой точке потенциального поля соответствует некоторое значение силы , действующей на тело, и некоторое значение потенциальной энергии U. Значит, между силой и U должна быть связь , с другой стороны, dA = –dU,

Система материальных точек. Уравнение поступательного движения системы материальных точек. Центр инерции

Совокупность тел, рассматриваемых как единое целое, называют механической системой.

Силы, с которыми взаимодействуют материальные точки системы между собой, называют внутренними силами. Силы, с которыми на материальные точки системы действуют тела, не входящие в данную систему (внешние тела), называют внешними силами.

Механическая система тел, на которую не действуют внешние силы, называется замкнутой, или изолированной, системой.

Для простоты рассуждений рассмотрим вначале систему, состоящую из двух материальных точек с массами и , которые расположены на оси абсцисс в точках с координатами и (рис. 1). Расстояние между этими точками . Точку С, которая делит это расстояние на отрезки, обратно пропорциональные массам, называют центром масс.

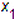
Следовательно, по определению

(1)

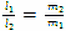
Пусть координата этой точки тогда . Подставим в уравнение (1), .

(2)

Формула (2) позволяет определить координату центра масс системы, состоящей из двух материальных точек.

Выражение (2) можно обобщить на систему n материальных точек, расположенных произвольным образом. Координата центра масс

(3)

Аналогичные выражения получаются и для координат и .

Положение центра масс можно также определить с помощью радиуса-вектора:

,

где и — масса и радиус-вектор i-й частицы.

При движении материальных точек системы координаты их изменяются. Записав выражение (3) для двух моментов времени и , вычтем одно из другого и получим:

Разделив обе части этого выражения на промежуток времени , имеем:

где — проекции на ось Ox векторов скорости движения центра масс и материальных точек 1, 2 . n.

Аналогичные выражения можно записать и для проекции скорости на оси Оу и Oz.

Выражение для нахождения скорости движения центра масс в векторном виде:

(4)

При движении материальных точек системы центр масс перемещается. Определим, от чего зависит характер движения центра масс.

Для этого рассмотрим систему двух материальных точек. Пусть на эти материальные точки действуют внешние силы и и эти точки взаимодействуют между собой силами (рис. 2).

Запишем для каждой материальной точки второй закон Ньютона:

Выразим ускорение точек через их начальные и конечные скорости:

Подставим полученные выражения во второй закон Ньютона:

Складывая эти равенства, имеем:

(5)

Поскольку по третьему закону Ньютона . Из формулы (4) получаем:

где — скорости движения центра масс в начальный момент времени и через промежуток времени . Тогда равенство (5) можно записать так:

(6)

Выражение (6) показывает, что изменить скорость движения центра масс системы материальных точек могут только внешние силы, внутренние силы изменяют скорости движения отдельных материальных точек.

Обозначим — суммарная масса материальных точек системы. Следовательно,

(7)

т. е. центр масс системы движется как материальная точка в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему. Выражение (7) представляет собой закон движения центра масс.

Если система материальных точек замкнутая, т. е.

Следовательно, центр масс замкнутой системы материальных точек движется равномерно и прямолинейно либо остается неподвижным независимо от того, как движутся отдельные материальные точки системы.

Так, если в инерциальной системе отсчета центр масс замкнутой системы был неподвижен в какой-то момент времени, то он будет оставаться в покое, несмотря на движение отдельных материальных точек системы в результате их взаимодействия.

Таким образом, центр масс (центр инерции) системы, положение которого характеризует распределение масс этой системы и определяется формулой (3), а скорость которого определяется формулой (4), является характерной точкой для системы, поведение которой подчиняется законам Ньютона и не зависит от природы сил взаимодействия в системе.

Понятие центра масс относится и к одиночному телу, которое можно представить как совокупность материальных точек. Центр масс тела можно рассматривать как точку (находящуюся внутри тела или вне его), в которой пересекаются линии действия сил, приводящих данное тело в поступательное движение. Центр масс тела совпадает с его центром тяжести.