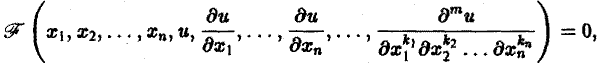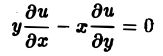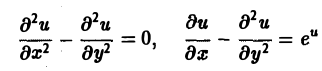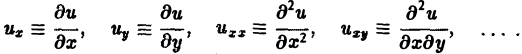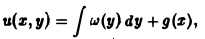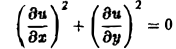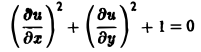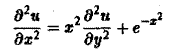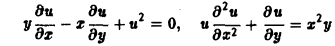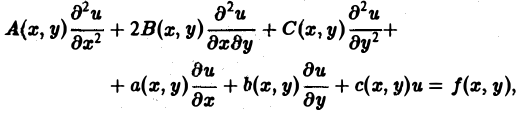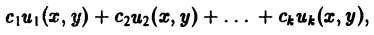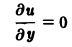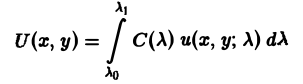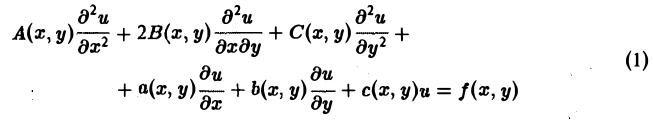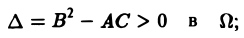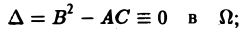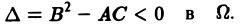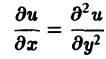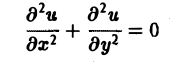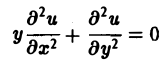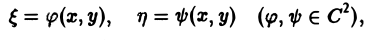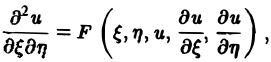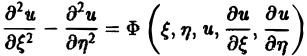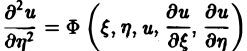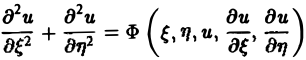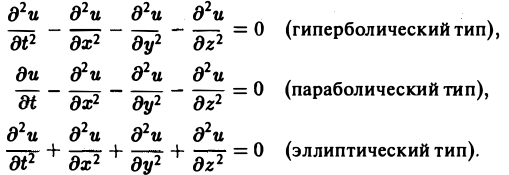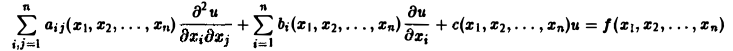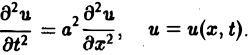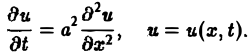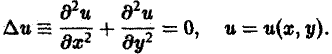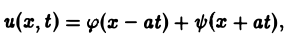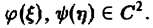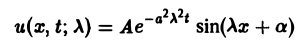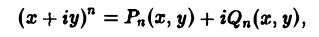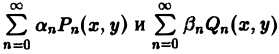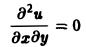Системы нелинейных дифференциальных уравнений в частных производных

РЕШЕНИЕ СИСТЕМЫ НЕЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА СО МНОГИМИ ПЕРЕМЕННЫМИ

Аширбаева А.Ж. 1 , Мамбетов Ж.И. 2

1 ORCID: 0000-0001-7706-0608, Доктор физико-математических наук, 2 ORCID: 0000-0003-4455-5887, Старший преподаватель,

1,2 Ошский технологический университет имени академика М.М. Адышева, г. Ош, Кыргызская Республика

РЕШЕНИЕ СИСТЕМЫ НЕЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА СО МНОГИМИ ПЕРЕМЕННЫМИ

Аннотация

Исследование системы нелинейных дифференциальных уравнений в частных производных первого порядка, методом характеристик, сводится к исследованию нелинейной системы интегральных уравнений, где всегда присутствует суперпозиция неизвестных функций. И найдя решение в характеристических переменных, для получения решения исходной задачи требуется перейти от характеристических переменных к исходным переменным. Последняя задача во многих случаях бывает настолько сложной, что её не решают, а принимают допустимость обратного преобразования переменных в качестве условия.

Целью данной работы является исследование решений системы нелинейных дифференциальных уравнений в частных производных первого порядка со многими переменными методом дополнительного аргумента, при помощи которого рассмотренная система уравнений приводится к системам интегральных уравнений. При этом в системе интегральных уравнений не присутствует суперпозиция неизвестных функций. Доказательство существования решения системы интегральных уравнений проводится с более строгим способом записи операторов в функциональных пространствах с использованием принципа «сжимающих отображений» для операторов запаздывающего типа.

Ключевые слова: уравнение в частных производных, система уравнений, начальные условия, дополнительный аргумент, оператор запаздывающего типа, принцип сжимающих отображений.

Ashirbaeva A.Zh. 1 , Mambetov Zh.I. 2

1 ORCID: 0000-0001-7706-0608, PhD in Physics and Mathematics, 2 ORCID: 0000-0003-4455-5887, Senior Lecturer,

1,2 Osh Technological University named after academician M. Adyshev, Osh, Kyrgyz Republic

SOLUTION OF SYSTEM OF NONLINEAR DIFFERENTIAL EQUATIONS IN PRIVATE FIRST ORDER WITH MULTIPLE VARIABLES

Abstract

The investigation of a system of first-order nonlinear partial differential equations by the method of characteristics reduces to the study of a nonlinear system of integral equations, where a superposition of unknown functions is always present. After finding a solution in the characteristic variables, in order to obtain the solution of the original problem, it is required to go from the characteristic variables to the original variables. The latter problem in many cases is so complex that it is unsolvable, but accept the possibility of inverse transformation of variables as a condition.

The aim of this paper is to investigate solutions of a system of nonlinear differential equations in first-order partial derivatives with many variable methods by an additional argument, by means of which the system of equations considered is reduced to systems of integral equations. In this case, the superposition of unknown functions is not present in the system of integral equations. The existence of a solution of integral equations system is proved with a more rigorous method of writing operators in function spaces using the principle of “contracting mappings” for operators of a retarded type.

Keywords: partial differential equation, system of equations, initial conditions, additional argument, delayed type operator, the principle of contracting mappings.

Введение

В настоящее время метод дополнительного аргумента (м.д.а.) развивается для систем нелинейных уравнений в частных производных (в.ч.п.) [4, С. 410-414], [5, С. 17-23] [10, С. 111-115]. М.И. Иманалиев в своей работе «Нелинейные интегро-дифференциальные уравнения с частными производными» [1, С. 55-100] c использованием разработанного м.д.а., на основе принципа «сжимающих отображений» различные нелинейные дифференциальные уравнения в частных производных (д.у. в ч.п.) с начальными условиями на оси были сведены к интегральным уравнениям (и.у.), и найдены достаточные условия существования и единственности в некоторых областях.

Аксиоматические основы этого метода были выявлены в работе П.С. Панкова, Т.М. Иманалиева [2, С. 30-34], где также введены соответствующие новые понятия и определения. Показано, что в м.д.а. основным является то, что дифференциальные операторы с частными производными являются в некотором смысле перестановочными с интегральными операторами, что было названо кратко «квазикоммутативностью».

М.д.а. применяется и для численного решения начальных задач для нелинейных д.у. в ч.п., при этом он имеет преимущества перед методами, использующими фиксированные сетки (не производится численное дифференцирование) и перед методами типа метода характеристик (расчет ведется не вдоль ломаных, а вдоль прямых). Кроме того, этот метод, как использующий результаты для и.у., более удобен для получения гарантированных результатов [8, С. 164].

Построена общая схема м.д.а. при исследовании широкого класса начальных задач для нелинейных операторно-дифференциальных уравнений (о.-д.у.) с композицией дифференциальных операторов любого порядка [9, С. 12-24]. Показана применимость этой схемы для различных конкретных типов уравнений, второго, третьего, четвертого, а также произвольного порядка [9, С. 52-76], в конце обобщается для уравнений со многими пространственными переменными [9, С. 91-123]. Для отдельных примеров получены решения в виде сходящихся рядов, также в случае, когда метод характеристик, как показано, применить невозможно [9, С. 59-61]. Предложенная схема реализована в виде компьютерной программы, произведены расчеты, показывающие возможности превосходства м.д.а. [3, С. 37-40].

Используя м.д.а. исследованы д.у. в ч.п. и и.-д.у. в ч.п. типа Кортевега-де Фриза, а также нелинейные волновые д.у. в ч.п. [6, С. 543-546], [7, С. 17-19].

Постановка задачи

В данной работе рассматривается следующая система нелинейных д.у. в ч.п.:

(1)

с начальными условиями

(2)

где через обозначены любые неизвестные функции:

Для определенности возьмем i=1,2,…,n

М.И. Иманалиев, С.Н. Алексеенко в работе [10, С. 111-115] рассматривали случай i=1,2,…,n.

Используем следующие обозначения:

– класс функций, определенных, непрерывных и ограниченных вместе со своими производными до порядка α по j-му аргументу, j=1,…,l, на некотором подмножестве Ω евклидова пространства R i , где мульти индекс (0,…,0) будем опускать [4, С. 410].

– класс функций, удовлетворяющих условию Липшица по переменной U с коэффициентом N, по переменной v с коэффициентом M,в случае функции одной переменной индекс будем опускать [9, С. 11].

Для удобства ссылок приведем известные результаты. Мы сформулируем их применительно к множествам банаховых пространств, как они будут использоваться в настоящей работе.

Лемма 1 (следствие принципа сжимающих отображений Банаха)

Если оператор A в шаре S= банахова пространства удовлетворяет условию ||Ax-Ay||≤ ½||x-y||, и ||A(0)||≤r, то он имеет в этом множестве точно одну неподвижную точку.

Лемма 2

Доказательство

Тогда в силу Леммы 1 решение в шаре существует.

Теорема

Тогда существует такое 0≤T*≤T, явно определяемое на основе исходных данных, что задача (1), (2) имеет единственное ограниченное во всей области G_n₊₁(T)=[0,T]×R n решение, которое совпадает при s=t с решением системы и у.

(3)

Доказательство

Представим основные этапы доказательства теоремы в виде лемм.

Лемма 3

В классе задача (1), (2) с – определяемых из

(4)

эквивалентна системе и.у.

(5)

(6)

Доказательство леммы 3

Из (4) следует (6) и следующие равенства

На основании последнего соотношения из (1) имеем

(7)

(8)

Определяя из (5) частные производные по t и x_k, k=1,…n с учетом (8) получаем (1).

Лемма 4

Пусть для i=1,…n функции , где являются решениями задачи (1), (2), а – решениями задачи (4) и они удовлетворяют системе и.у. (3), и наоборот, если функции являющиеся решениями системы и.у. (3), непрерывно дифференцируемы по всем своим аргументам, то в пределах некоторого интервала изменения переменной t, определяемого на основе исходных данных, при s=t ,будет удовлетворять системе д.у. в ч.п. (1) и начальному условию (2).

Доказательство леммы 4

Пусть функции , , i=1, 2…n являются решениями задач (1), (2) и (4). В силу леммы 3 они удовлетворяют равенствам (7) и (6). Подставив , i=1, 2…n из (6) в (7), получим систему и.у.

Обозначив приходим к (3).

Напротив, пусть непрерывно дифференцируемые функции , i=1, 2…n обращают систему и.у. (3) в тождество.

Непосредственным дифференцированием из (3) выводится тождество

На основании этого тождества определяется интервал изменения аргумента t, в котором W=0. Кроме этого, из (3) вытекает, что . С учетом отмеченных фактов, подставляя в (1) и (2), убеждаемся, что на всем интервале изменения t, на котором W=0, удовлетворяют начальной задаче (1), (2).

Лемма 5

Существует такое T*>0, что система и.у. (3) имеет единственное решение, принадлежащее

Доказательство леммы 5

Записываем систему и.у. (3) в виде одного (векторного) равенства – вектор-функция от переменных , с компонентами-искомыми функциями , а компоненты оператора определены равенствами:

Таким образом, условия Леммы 2 выполнены и мы заключаем, что уравнение (3) имеет решение в пространстве функций с нормой, не превышающей 2Ω₀(T * ). Доказательство теоремы проведено.

Заключение

Получены достаточные условия существования и единственности решения начальной задачи для системы нелинейных д.у. в ч.п. первого порядка со многими переменными. Полученные результаты свидетельствуют о том, что м.д. а. применяется и для решения системы нелинейных д.у. в ч.п. Приведенную схему применения м.д.а. для решения системы нелинейных д.у. в ч.п. можно использовать при решении системы нелинейных уравнений других классов.

Список литературы / References

Иманалиев М.И. Нелинейные интегро-дифференциальные уравнения с частными производными / М.И.Иманалиев. – Бишкек: Илим, 1992. – 112 с.
Панков П.С. Квазикоммутативность дифференциальных операторов и ее приложение к обоснованию метода дополнительного аргумента / П.С. Панков, Т.М. Иманалиев // Исследования по интегро-дифференциальным уравнениям, Выпуск. 28. – Бишкек: Илим, 1999. – С. 30 – 34.
Аширбаева А.Ж. Приближенное решение начальной задачи для нелинейных дифференциальных уравнений в частных производных второго порядка методом дополнительного аргумента / А.Ж. Аширбаева // Исследования по интегро-дифференциальным уравнениям. – Бишкек: Илим, 2014. – Выпуск. – С. 37 – 40.
Иманалиев М.И. К теории нелинейных интегро-дифференциальных уравнений в частных производных типа Уизема/ М.И. Иманалиев, С.Н. Алексеенко // Доклады Российской АН. – 1992. – Т. 323. – № 3. – С. 410 – 414.
Иманалиев М.И. К теории почти солитонных решений нелинейного дифференциального уравнения в частных производных типа Кортевега-де Фриза четвертого порядка / М.И. Иманалиев, Т.М. Иманалиев, У.М. Иманалиев // Исследования по интегро-дифференциальным уравнениям. – Бишкек: Илим, 2003. – Выпуск 32. – С.17 – 23.
Иманалиев М.И. К теории нелинейных уравнений с дифференциальным оператором типа полной производной по времени / М.И. Иманалиев, С.Н. Алексеенко // Доклады Российской АН. – 1993. – Т. 329. – № 5. – С. 543 – 546.
Иманалиев М.И. К теории нелинейных дифференциальных уравнений в частных производных типа Кортевега – де Фриза / М.И. Иманалиев, П.С. Панков, Т.М. Иманалиев // Доклады Российской АН. – 1995. – Т. 342. – № 1. – С.17 – 19.
Панков П.С. Приближенное решение начальной задачи для нелинейных дифференциальных уравнений в частных производных методом дополнительного аргумента / П.С.Панков, Т.М. Иманалиев, Г.М. Кененбаева // Юбилейная научная конференция, посвященная 50-летию развития математики в Академии наук Казахстана: Тезис, доклады – Алматы, 1995. – С. 164.
Аширбаева А.Ж. Решение нелинейных дифференциальных и интегро-дифференциальных уравнений в частных производных высокого порядка методом дополнительного аргумента. – Бишкек: Илим, 2013. – 134 с.
Иманалиев М.И. К теории систем нелинейных интегро-дифференциальных уравнений в частных производных типа Уизема / М.И. Иманалиев, С.Н. Алексеенко // Доклады АН. – – Т. 325. – № 6. – С.1111 – 1115.

Список литературы на английском языке / References in English

Дифференциальные уравнения в частных производных с примерами решения и образцами выполнения

Дифференциальным уравнением с частными производными называется уравнение вида
(1)

связывающее независимые переменные x1, х2, … , хn искомую функцию и = и(х1, х2,…, хn) и ее частные производные (наличие хотя бы одной производной обязательно). Здесь ki,k2,… ,кn — неотрицательные целые числа, такие, что к1 + к2 + … + кп = т.

Порядком дифференциального уравнения называется наивысший порядок входящие в уравнение частных производных. Так, если х, у — независимые переменные, и = и(х, у) — искомая функция, то

— дифференциальное уравнение 1-го порядка;

— дифференциальные уравнения 2-го порядка.

Для упрощения записи пользуются также следующими обозначениями:

Пусть имеем дифференциальное уравнение с частными производными (1) порядка т. Обозначим через С m (D) множество функций, непрерывных в области D вместе со всеми производными до порядка m включительно.

Определение:

Решением дифференциального уравнения (1) в некоторой области D изменения независимых переменных x1, x2…xn,. называется всякая функция и = и(х1, х2,…, xп) ∈ С m (D) такая, что подстановка этой функции и ее производных в уравнение (1) обращает последнее в тождество по x1, x2, …., хп в области D.

Пример:

Найти решение и = и(х,у) уравнения

Равенство (2) означает, что искомая функция и не зависит опт х, но может быть любой функцией от у,

u = φ(y). (3)

Таким образом, решение (3) уравнения (2) содержит одну произвольную функцию. Это — общее решение уравнения (2).

Приме:

Найти решение u = u(z, у) уравнения

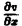
Положим = о. Тогда уравнение (4) примет вид = 0. Его общим решением будет произвольная функция v = w(у). Поскольку v= приходим к уравнению = w(у). Интегрируя по у (считая х параметром), получим

где g(x) — произвольная функция. Так как w(у) — произвольная функция, то и интеграл от нее также является произвольной функцией; обозначим его через f(у). В результате получим решение уравнения (4) в виде

u(x, y) = f(y) + g(x) (5)

произвольные дифференцируемые функции).

Решение (5) уравнения с частными производными 2-го порядка (4) содержит уже две произвольные функции. Его называют общим решением уравнения (4), так как всякое другое решение уравнения (4) может быть получено из (5) подходящим выбором функций f и g.

Мы видим, таким образом, что уравнения с частными производными имеют целые семейства решений. Однако существуют уравнения с частными производными, множества решений которых весьма узки и, в некоторых случаях, да же пусты.

Пример:

Множество действительных решений уравнения

исчерпывается функцией u(x, y) = const, а уравнение

вовсе не имеет действительных решений.

Мы не ставим пока вопрос об отыскании частных решений. Позже будет выяснено, какие дополнительные условия нужно задать, чтобы с их помощью можно было выделить частное решение, т.е. функцию, удовлетворяющую как дифференциальному уравнению, так и этим дополнительным условиям.

Линейные дифференциальные уравнения с частными производными. Свойства их решений

Уравнение с частными производными называется линейным, если оно линейно относительно искомой функции и всех ее производных, входящих в уравнение; в противном случае уравнение называется нелинейным.

Пример:

— линейное уравнение; уравнения

Линейное дифференциальное уравнение 2-го порядка для функции двух независимых переменных х, у в общем случае имеет вид
(1)

где А(х, у), В(х, у), …, с(х,у), f(x,y) — функции переменных х, у, заданные в некоторой области D плоскости хОу. Если f(x,y) ≡ 0 в D, то уравнение (1) называется однородным, в противном случае — неоднородным.

Обозначив левую часть уравнения (1) через L[u], запишем (1) в виде

L[u] = f(x, у). (2)

Соответствующее однородное уравнение запишется так:

L[u] = 0. (3)

Здесь L — линейный дифференциальный оператор, определенный на линейном пространстве C 2 (D) функций и = и(х, у).

Пользуясь свойством линейности оператора L, легко убедиться в справедливости следующих теорем, выражающих свойства решений линейных однородных дифференциальных уравнений с частными производными.

Теорема:

Если и(х, у) есть решение линейного однородного уравнения (3), то си(х, у), где с — любая постоянная, есть также решение уравнения (3).

Теорема:

Если и₁(х, у) и и₂(х, у) — решения линейного однородного уравнения (3), то сумма и₁(х, у) + и₂(x, у) есть также решение этого уравнения.

Следствие:

Если каждая из функций и₁(х, у) и и₂(х, у), u k(x, у) является решением уравнения (3), то линейная комбинация

где c1, c2 …, сk — произвольные постоянные, также является решением этого уравнения.

В отличие от обыкновенного линейного однородного дифференциального уравнения, имеющего конечное число линейно независимых частных решений, линейная

комбинация которых дает общее решение этого уравнения, уравнение с частными производными может иметь бесконечное множество линейно независимых частных решений.

Пример:

имеет общее решение k = φ(х), так что решениями его будут, например, функции 1,х,…, х n ,… . В соответствии с этим в линейных задачах для уравнений с частными производными нам придется иметь дело не только с линейными комбинациями конечного числа решений, но и с рядами 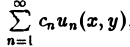, членами которых являются произведения постоянных Сп на частные решения иn(х, у) дифференциального уравнения.

Возможны случаи, когда функция и(х, у; λ) при всех значениях параметра λ из некоторого интервала (λо, λ1), конечного или бесконечного, является решением уравнения (3). В этом случае говорят, что решения уравнения зависят от непрерывно меняющегося параметра λ. Если теперь взять функцию С(λ) такую, что первые и вторые производные интеграла

по х и по у могут быть получены с помощью дифференцирования под знаком интеграла, то этот интеграл также будет решением уравнения (3). Для линейного неоднородного уравнения

L[u] = f (4)

справедливы следующие предложения.

Теорема:

Если и(х, у) есть решение линейного неоднородного уравнения (4), a v(x, у) — решение соответствующего однородного уравнения (3), то сумма и + v есть решение неоднородного уравнения (4).

Теорема:

Принцип суперпозиции. Если и1(х, у) —решение уравнения L[u] = f1, a u2(x,y) — решение уравнения L[u] = f2, то и1 + u2 — решение уравнения L[u] = f1 + f2.

Классификация линейных дифференциальных уравнений второго порядка с двумя независимыми переменными

Определение:

Линейное дифференциальное уравнение второго порядка

в некоторой области Q на плоскости хОу называется

1) гиперболическим в Ω, если

2) параболическим в Ω, если

3) эллиптическим в Ω, если

Пользуясь этим определением, легко проверить, что уравнения

— гиперболические при всех х и у, уравнение

— параболическое при всех х и у, а уравнение

— эллиптическое при всех х и у. Уравнение

— эллиптическое при у > 0, параболическое на линии у = 0 и гиперболическое в полуплоскости у

с помощью которой уравнение (1) преобразуется к более простому, каноническому виду, своему для каждого типа уравнения.

Уравнение гиперболического типа (∆ > 0) преобразуется к вшу

(два канонических вида уравнений гиперболического типа).

Уравнение параболического типа (∆ ≡ 0) преобразуется к виду

(канонический вид уравнения параболического типа).

Уравнение эллиптического типа (∆

(канонический вид уравнения эллиптического типа). Здесь F и Ф — некоторые функции, зависящие от искомой функции и, ее первых производных 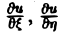и независимых переменных ξ, η. Вид функций F и Ф определяется исходным уравнением (1).

В некоторых случаях каноническая форма уравнения позволяет найти общее решение исходного уравнения.

Как правило, приведениеуравнения(1) к каноническому виду путем замены независимых переменных имеет локальный характер, т. е. осуществимо лишь в некоторой достаточно малой окрестности рассматриваемой точки Mo(xo, уo).

Когда число п независимых переменных больше двух, также различают уравнения гиперболического, параболического и эллиптического типов. Например, при п = 4 простейшая каноническая форма таких уравнений имеет вид

Здесь и = и(х, у, z, t).

Замечание:

В общем случае, когда число независимых переменных больше двух, приведение линейною уравнения с переменными коэффициентами

к каноническому виду возможно только в данной точке 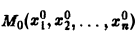и невозможно в любой сколь угодно малой окрестности этой точки.

Мы ограничимся рассмотрением линейных дифференциальных уравнений 2-го порядка. К таким уравнениям приводит большое количество различных физических задач.

Так, колебательные процессы различной природы (колебания струн, мембран, акустические колебания газа в трубах, электромагнитные колебания и т. д.) описываются уравнениями гиперболического типа. Простейшим из таких уравнений является уравнение колебаний струны (одномерное волновое уравнение): (2)

Здесь х — пространственная координата, t — время, 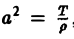где Т — натяжение струны, р — ее линейная плотность.

Процессы теплопроводности и диффузии приводят к уравнениям параболического типа. В одномерном случае простейшее уравнение теплопроводности имеет вид
(3)

Здесь 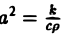где р — плотность среды, с — удельная теплоемкость, k — коэффициент теплопроводности.

Наконец, установившиеся процессы, когда искомая функция не зависит от времени, определяются уравнениями эллиптического типа, типичным представителем которых является уравнение Лапласа
(4)

Непосредственной проверкой убеждаемся в том, что решением уравнения (2) является всякая функция и(х, t) вида

Можно показать, что решениями уравнения (3) являются функции вида

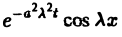
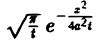
произвольные постоянные, А — числовой параметр). Интегрируя решение и(х, t; λ) = уравнения (3) по параметру λ в пределах от — ∞ до + ∞ , получим так называемое фундаментальное решение U(x, t) = уравнения теплопроводности.

Наконец, нетрудно убедиться, что действительнозначные функции Рn(х,у) и Qn(x, у), определяемые из соотношения

являются решениями уравнения Лапласа (4) для п = 0, 1, 2…..Этот последний результат есть частный, случай общего утверждения, что и действительная и мнимая части аналитической функции

f(z) = u(x, у) + iv(x, у)

комплексного переменного z = х + iy являются решениями уравнения Лапласа (4).

В силу линейности уравнения (4) ряды

тоже будут решениями уравнения (4), если они сходятся равномерно, как и ряды, полученные из них двукратным почленным дифференцированием по каждому из аргументов х, у.

Таким образом, для простейшей — канонической — формы уравнений гиперболического, параболического и эллиптического типов мы располагаем о решениях этих уравнений некоторой информацией.

Постановка основных задач для линейных дифференциальных уравнений второго порядка

Для полного описания того или иного физического процесса мало иметь только дифференциальное уравнение процесса, надо еще задать начальное состояние этого процесса (начальные условия) и режим на границе S той области Ω, в которой процесс происходит (граничные условия). Это обусловлено неединственностью решения дифференциальных уравнений.

Пример:

Общее решение уравнения

имеет вид и(х, у) = f(x) + g(y), где f(x) и g(y) — произвольные дифференцируемые функции. Поэтому чтобы выделить решение, описывающее данный физический процесс, необходимо задать дополнительные условия.

Различают три основных типа задач для дифференциальных уравнений с частными производными (число независимых переменных равно п):

а) задача Коши для уравнений гиперболического и параболического типов: задаются начальные условия, область Ω совпадает со всем пространством R n , граничные условия отсутствуют;

б) краевая задача для уравнений эллиптического типа: задаются граничные условия на границе S области Ω, начальные условия отсутствуют;

в) смешанная задача для уравнений гиперболического и параболического типов: задаются начальные и граничные условия, Ω ≠ R n

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

источники:

http://lfirmal.com/differencialnye-uravneniya-v-chastnyh-proizvodnyh/