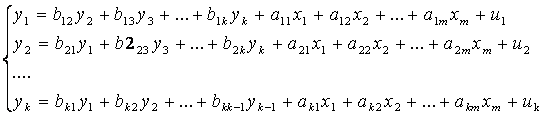Системы одновременных уравнений в r

Системы эконометрических уравнений

Пример . Рассмотрим модель зависимости общей величины расходов на питание от располагаемого личного дохода (х) и цены продуктов питания (р):у = а₀ + а₁х + а₂р + ε. Определим класс модели и вид переменных модели: регрессионная модель с одним уравнением; эндогенная переменная — расходы на питание, экзогенные переменные — располагаемый личный доход и цена продуктов питания.

Принципиальные сложности применения систем эконометрических уравнений связаны с ошибками спецификации модели.

Система уравнений в эконометрических исследованиях может быть построена по-разному. Выделяют следующие 3 вида систем уравнений.

1. Система независимых уравнений, когда каждая зависимая переменная (y ) рассматривается как функция только от предопределенных переменных (х):
   
2. Система рекурсивных уравнений, когда в каждом последующем уравнении системы зависимая переменная представляет функцию от зависимых и предопределенных переменных предшествующих уравнений:

От структурной формы легко перейти к так называемой приведенной форме модели. Число уравнений в приведенной форме равно числу эндогенных переменных модели. В каждом уравнении приведенной формы эндогенная переменная выражается через все предопределенные переменные модели:

Так как правая часть каждого из уравнений приведенной формы содержит только предопределенные переменные и остатки, а левая часть только одну из эндогенных переменных, то такая система является системой независимых уравнений. Поэтому параметры каждого из уравнений системы в приведенной форме можно определить независимо обычным МНК.
Зная оценки этих приведенных коэффициентов можно определить параметры структурной формы модели. Но не всегда, а только если модель является идентифицируемой.

Проблема идентификации

Количество структурных и приведенных коэффициентов одинаково в модели идентифицируемой.

Правила идентификации

Ранг данной матрицы равен 1, что меньше К-1=2, следовательно, 1-ое уравнение модели неидентифицированно.
Составим матрицу А для 2-ого уравнения системы. Во 2-ом уравнении отсутствуют переменные y₃, x₂, х₃:
y₃ x ₂ x₃
b₁₃ a ₁₃ 0 — в 1-ом уравнении
1 a₃₂ a₃₃ — в 3-ем уравнении
Ранг данной матрицы равен 2, что равно К-1=2, следовательно, 2-ое уравнение модели точно идентифицированно.
Составим матрицу А для 3-его уравнения системы. В 3-ем уравнении отсутствуют переменные y₁, x₂:
y ₁ x ₂
1 a₁₂ — в 1-ом уравнении
b₂₁ 0 — во 2-ом уравнении
Ранг данной матрицы равен 1, что меньше К-1=2, следовательно, 3-е уравнение модели неидентифицированно.

Сделаем выводы: 1-ое и 3-е уравнения системы неидентифицированны (т.к. не выполняются достаточные условия идентификации, а в случае 1-ого уравнения и необходимое условие также). 2-ое уравнение системы сверхидентифицированно. Следовательно, система в целом является неидентифицируемой.
Для оценки параметров 2-ого уравнения можно применить двухшаговый МНК. Параметры 1-ого и 3-его уравнений определить по коэффициентам приведенной формы нельзя. Поэтому модель должна быть модифицирована.

Система одновременных эконометрических уравнений

Вы будете перенаправлены на Автор24

Общие сведения о системе одновременных эконометрических уравнений

Система одновременных экономических уравнений – это совокупность уравнений, которые позволяют исследователям установить наличие и степень связи (взаимозависимости) между эконометрическими переменными.

Выделяют две группы экономических переменных, из которых образуют эконометрические уравнения:

• эндогенные переменные, чьи значения определяют в результате функционирования изучаемой экономической системы (эндогенные переменные зависят как от экзогенных, так и от других эндогенных переменных);
• экзогенные переменные, чьи значения задаются извне (т.е. определяются вне эконометрической модели) и являются основой для определения значений эндогенных переменных (экзогенные переменные являются независимыми).

Функционирование сложных экономических систем может быть объяснено благодаря построению изолированных уравнений регрессии и измерению на их основе тесноты связи между переменными. Однако истинное влияние отдельных признаков на вариацию результирующей переменной не может быть описано одним отдельно взятым уравнением регрессии. В связи с этим в изучении экономических процессов важное значение приобрело структурирование связей между системой переменных.

В качестве примера системы одновременных эконометрических уравнений можно привести простейшую макроэкономическую (кейнсианскую) модель, которая состоит из двух уравнений:

В данной модели эндогенными переменными являются C (расходы на потребление) и Y (доход), а экзогенной переменной – I (инвестиции). b представляет собой коэффициент, который выражает предельную склонность к потреблению.

Характеристика структурной и приведенной форм системы уравнений

Данная система от всех других систем уравнения отличается наличием определенной структурной формы эконометрической модели. Это форма предполагает, что в правых и левых частях разных уравнений системы находятся одни и те же экономические переменные. Структурная форма системы одновременных эконометрических уравнений в случае переноса всех эндогенных переменных в левую часть может быть представлено в следующем матричном виде: YA = XB + E.

Готовые работы на аналогичную тему

Кроме структурной также выделяют приведенную (прогнозную) форму системы. По сути она есть представление системы, в котором эндогенные переменные выражены через экзогенные, то есть в каждом уравнении имеется только одна эндогенная переменная. Тогда она выглядит так: Y = XП + U.

Приведенную форму системы всегда можно получить, если задана структурная форма. Однако обратное действие не всегда возможно, а если оно и возможно, то не всегда получается однозначный результат.

Если через коэффициенты приведенной формы можно выразить коэффициенты структурного уравнения, то оно называется идентифицируемым (в противном случае оно – неидентифицируемое). Точная индентифицируемость свойственна ситуации, когда способ подобного выражения является единственным. Если же их несколько, то говорят о сверхидентифицируемости.

Чтобы имела место идентифицируемость, требуется выполнение такого необходимого условия, как непревышение количества переменных правой части уравнения над количеством всех экзогенных переменных системы. Формулировка этого условия может отличаться. Так, часто говорят: количество экзогенных переменных, которые исключены из данного уравнения, должно быть не меньше количества эндогенных переменных, которые включены в уравнение, за вычетом единицы.

Также выделяют условие, достаточное для признания идентифицируемости системы. Оно заключается в том, чтобы общее число эндогенных переменных системы за вычетом единицы не превышало ранг матрицы, который составлен из коэффициентов (в других уравнениях) при переменных, отсутствующих в данном уравнении.

Методы оценки систем одновременных эконометрических уравнений

Для того, чтобы оценить представленные в структурной форме уравнения системы, нецелесообразно непосредственно применять обычный метод наименьших квадратов. Это связано с тем, что подобное применение нарушит важнейшее условие регрессионного анализа — экзогенность (предопределенность, независимость) факторов. Тогда будут получены смещённые и несостоятельные оценки параметров.

Поэтому системы одновременных эконометрических уравнений оценивают посредством применения следующих методов:

• косвенный метод наименьших квадратов – подстановка в аналитическое выражение зависимости структурных коэффициентов от их приведённых оценок, которые получают в результате применения обычного метода наименьших квадратов;
• двухшаговый метод наименьших квадратов – оценивание сначала зависимости эндогенных переменных от всех экзогенных (первый шаг), а затем – структурной формы модели, в которой эндогенные переменные заменены на их оценки, полученные на первом шаге (второй шаг);
• трехшаговый метод наименьших квадратов – предыдущий метод дополняется третьим шагом, с помощью которого оценивают ковариационную матрицу вектора случайных ошибок системы уравнений;
• методы максимального правдоподобия – использование всей информации об ограничениях на приведённую форму эконометрической модели.

Системы одновременных уравнений

Системы эконометрических уравнений включают множество зависимых или эндогенных переменных и множество предопределенных переменных (лаговые и текущие независимые переменные, а также лаговые эндогенные переменные). Как и эконометрические модели с одним уравнением, системы эконометрических уравнений направлены на объяснение текущих значений эндогенных переменных в зависимости от значений предопределенных переменных. В эконометрическом моделировании выделяют три вида систем уравнений.

1. Система независимых уравнений определяется тем, что каждая эндогенная переменная y является функцией только от одних и тех же переменных x:

(1)

2. Система рекурсивных уравнений определяется тем, что в каждом последующем уравнении эндогенная переменная выступает в качестве экзогенной переменной:

(2)

В таких системах каждое уравнение может рассматриваться самостоятельно, и неизвестные коэффициенты таких уравнений можно найти с помощью классического метода наименьших квадратов.

3. Система взаимозависимых уравнений определяется тем, что эндогенные переменные в одних уравнениях входят в левую часть(т. е. являются результативными признаками), а в других уравнениях — в правую часть (т. е. являются факторными признаками):

(3)

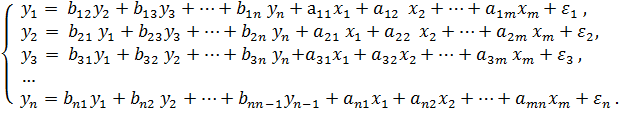
В системе взаимозависимых уравнений значения результативных и факторных переменных формируются одновременно под влиянием внешних факторов. Эта система — система одновременных, или совместных, уравнений.

Каждое уравнение системы одновременных уравнений не может рассматриваться как самостоятельная часть системы, вследствие чего применение традиционного метода наименьших квадратов для определения его параметров невозможно, так как нарушаются условия МНК:

1) одновременная зависимость между переменными модели, т. е. в первом уравнении y₁ — это функция от y₂, а во втором уравнении y₂ — это функция от y₁;

2) проблема мультиколлинеарности, т. е. во втором уравнении системы y₂ зависит от x₁, а в других уравнениях обе переменные выступают в качестве факторных;

3) случайные ошибки уравнения коррелируют с результативными переменными.

В результате применения обычного МНК к оцениванию одновременных уравнений оценки неизвестных параметров получаются смещенными и несостоятельными.

Часто приводимым примером системы взаимозависимых уравнений является моделирование одновременного формирования спроса Q d и предложения Q s товара в зависимости от его цены P в момент времени t:

где — предложение товара в момент времени t;

— спрос на товар в момент времени t;

P_t — цена товара в момент времени t;

P_t-1 — цена товара в предшествующий момент времени (t − 1);

I_t — доход потребителей в момент времени t.

Если рынок находится в состоянии равновесия, то имеет место следующее тождество равновесия:

1.1 Структурная и приведенная формы системы одновременных уравнений. Проблема идентификации модели.

Уравнения, из которых состоит исходная система одновременных уравнений, называются структурными уравнениями, а модель в данном случае имеет структурную форму. С помощью структурной формы модели непосредственно отражают реальный экономический процесс. Коэффициенты уравнений структурной формы называются структурными коэффициентами, или параметрами.

Структурные уравнения могут быть представлены либо поведенческими уравнениями, либо уравнениями — тождествами.

Поведенческие уравнения характеризуют все типы взаимодействия между эндогенными и экзогенными переменными.

Эндогенные переменные – это зависимые переменные, число которых равно числу уравнений в системе. Они обозначаются через y.

Экзогенные переменные – это предопределенные переменные, влияющие на эндогенные переменные, но не зависящие от них. Они обозначаются через x.

В поведенческих уравнениях значения параметров являются неизвестными и подлежат оцениванию. Примером поведенческого уравнения является уравнения спроса или предложения:

= a₀ +a₁ ×P_t +a₂ ×P_t−1 или = b₀ +b₁ ×P_t +b₂ ×I_t .

Тождествами называют равенства, выполняющиеся во всех случаях. Для них характерно, что их вид и значения параметров известны и они не содержат случайной компоненты. Примером уравнения тождества является тождество равновесия в модели «спрос — предложение»: .

Для определения неизвестных структурных параметров системы одновременных уравнений переходят к приведенной форме модели.

Приведенной формой модели называется система независимых уравнений, в которой все эндогенные переменные выражены только через экзогенные или предопределенные переменные и случайные компоненты, например:

(5)

Коэффициенты приведенной формы называются приведенными коэффициентами, или параметрами, которые можно оценить традиционным методом наименьших квадратов. С помощью МНК оценок приведенных коэффициентов определяются оценки структурных коэффициентов.

При переходе от структурной формы модели к приведенной форме возникает проблема идентификации модели.

Проблема идентификации заключается в возможности численной оценки неизвестных коэффициентов структурных уравнений по МНК оценкам коэффициентов приведенных уравнений. Исходная система одновременных уравнений является идентифицированной, если все ее уравнения точно идентифицированы. Уравнение является точно идентифицированным, если по оценкам коэффициентов приведенной модели можно однозначно найти оценки коэффициентов структурной модели. Признаком идентифицированности системы является равенство между количеством уравнений, определяющих структурные коэффициенты, и количеством этих коэффициентов, т. е. когда структурная система уравнений является квадратной.

Исходная система одновременных уравнений является сверх идентифицированной, если среди уравнений модели есть хотя бы одно сверхидентифицированное. Уравнение является сверхидентифицированным, если по оценкам коэффициентов приведенной модели можно получить более одного значения для коэффициентов структурной модели.

Исходная система одновременных уравнений является неидентифицированной, если среди уравнений модели есть хотя бы одно неидентифицированное. Уравнение является неидентифицированным, если по оценкам коэффициентов приведенной модели невозможно рассчитать оценки коэффициентов структурной модели.

Необходимые и достаточные условия идентификации модели

Необходимые и достаточные условия идентификации применяются только к структурной форме модели.

1) N — количество предопределенных переменных в модели;

2) n — количество предопределенных переменных в уравнении, проверяемом на идентифицируемость;

3) M — количество эндогенных переменных в модели;

4) m — количество эндогенных переменных в уравнении, проверяемом на идентифицируемость;

5) K — матрица коэффициентов при переменных, не входящих в уравнение, проверяемое на идентифицируемость.

Первое необходимое условие идентифицируемости уравнения модели.

Уравнение модели идентифицируемо в том случае, если оно исключает хотя бы N − 1 предопределенную переменную модели, т. е.:

Второе необходимое условие идентифицируемости уравнения модели.

Уравнение модели идентифицируемо в случае, если количество предопределенных переменных, не входящих в данное уравнение, будет не меньше числа эндогенных переменных этого уравнения минус единица, т. е.:

Достаточное условие идентифицируемости уравнения модели.

Уравнение модели идентифицируемо в случае, если ранг матрицы K равен N − 1.

Ранг матрицы — размер наибольшей ее квадратной подматрицы, определитель которой не равен нулю.

Исходя из перечисленных условий идентификации можно сформулировать необходимые и достаточные условия идентифицируемости уравнения модели:

1) если M − m > n − 1 и ранг матрицы K равен N − 1, то уравнение модели считается сверхидентифицированным;

2) если M − m = n − 1 и ранг матрицы K равен N − 1, то уравнение модели считается точно идентифицированным;

3) если M − m ≥ n − 1 и ранг матрицы K меньше N − 1, то уравнение модели считается неидентифицированным;