Системы решения уравнений на нигме

Нигма — поисковая система Nigma с уклоном в математику, химию, поиск музыки и многое другое

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня речь пойдет про очередную поисковую систему, которая когда-то называлась Nigma, но после ввода кириллических доменов претерпела ребрендиг и теперь гордо пишется русскими буквами — Нигма.рф.

Чуть раньше вы могли читать мои обзоры мастодонтов рынка поиска рунета: Яндекса и занимающего второе место по популярности среди русскоязычного интернет сообщества Гугла. Обзоры те были объемными и соразмерными с масштабами этих поисковиков.

Чуть менее подробно я писал про Майл, который частично использует выдачу Гугла, и про поиск Рамблера, который, в свою очередь, полностью перешел в нахлебники к Яндексу.

Еще менее подробно я коснулся мастодонтов из поискового мира буржунета: Яхуу, который сейчас использует выдачу Бинга, ну и сам, Bing, который серьезно увеличил свою долю после ассимиляции с Yahoo. Спел я реквием и Апорту, который почил в бозе и чей домен был продан за гроши под какой-то магазинчик.

Герой же сегодняшнего обзора по сути никогда не был на олимпе или даже близко к нему (в отличии от упомянутых выше систем), но тем не менее достоин внимания, ибо есть у него свои фичи, которых нет у других, и не смотря на скромные финансовые и людские ресурсы Нигма продолжает существовать как поисковая система в рунете и даже пытается осуществить экспансию (это как?) на рынок Вьетнама.

Принципы работы и отличия поисковой системы Nigma

Во-первых, сразу же хочу объяснить, почему я назвал Nigma надстройкой над популярными поисковиками. У них есть свой поисковый робот, который индексирует интернет (или только рунет), но кроме собственной индексной базы разработчики активно используют и общедоступные базы других систем (на данный момент, после выпадения Апорта из обоймы, остались Яндекс, Гугол, Рамблер, Бинг, Яху, Альтависта).

Насколько велика в этом многообразии данных доля базы самой Нигмы — остается загадкой. Но опираясь на достаточно скромные людские ресурсы (несколько десятков сотрудников, если я не ошибаюсь) и, наверное, скромные финансовые возможности, расходы на индексирование рунета своими силами должны быть небольшими, ибо в противном случае можно запросто вылететь в трубу.

Собственно, данный проект и задумывался, как некий инструмент раскладывающий выдачу по полочкам (категориям). Называется это действо в Nigma кластеризация и подразумевает она под собой следующее. Общая выдача по запросу пользователя имеет обычно чудовищные размеры и задача поиска в этом случае заключается в подборе и выдаче наиболее релевантных запросу пользователя документов (ссылок на них с заголовком и небольшим описанием — сниппетом).

Но не всегда понятно, что именно хотел видеть пользователь на первых местах в выдаче. В большинстве случаев имеет место быть многозначность (Яндекс с недавних пор частично решает эту проблему с помощью технологии Спектр). Поэтому разработчики решили вместе с общей выдачей по запросу предлагать пользователям еще и фильтры Нигмы, которые позволили бы либо выделить определенные кластеры, либо, наоборот, какие-то из них убрать из выдачи.

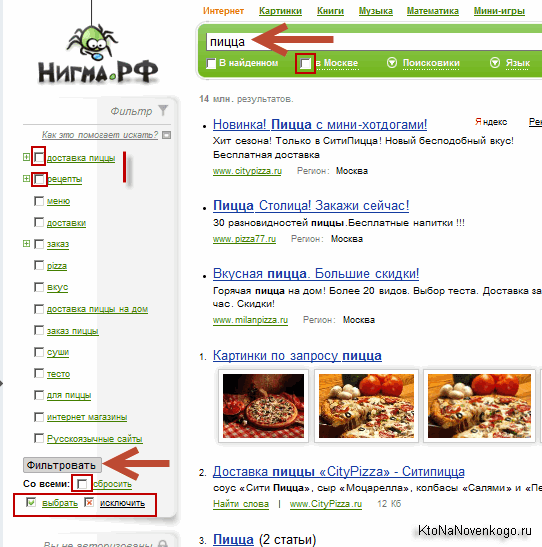
Выглядит это безобразие примерно так:

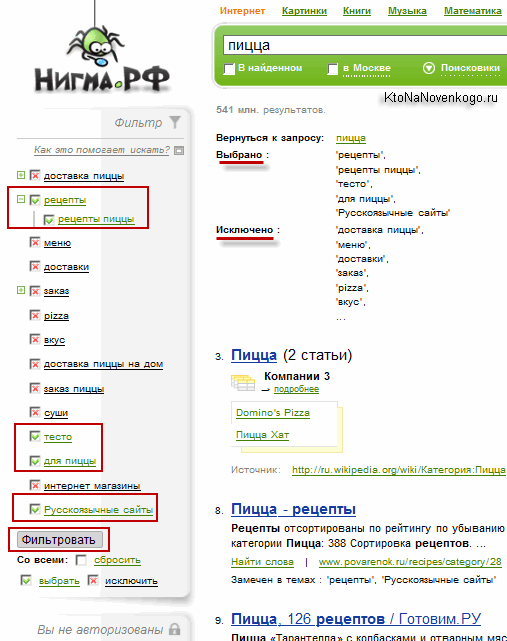
Слева выводится набор фильтров. Щелчок в чекбоксе напротив нужного кластера приводит к исключению его из поиска (крестик ставится), повторный щелчок, наоборот, приводит к обязательном показу этого кластера и так по кругу. Таким образом в Nigma можно довольно быстро и просто отфильтровать огромную выдачу по запросу и повысить ее релевантность для себя любимого:

Собственно, это и стало основной идеей, которая побудила разработчиков к созданию новой поисковой системы. Концепцию создания поисковика предложил бывший сотрудник Майла по фамилии Лавренко, а реализовал ее тогда еще студент последнего курса Высшей математики и кибернетики МГУ Владимир Чернышов и иже с ним. Дело был в 2004 году, а уже в начале апреля 2005 открылся сайт Nigma.ru.

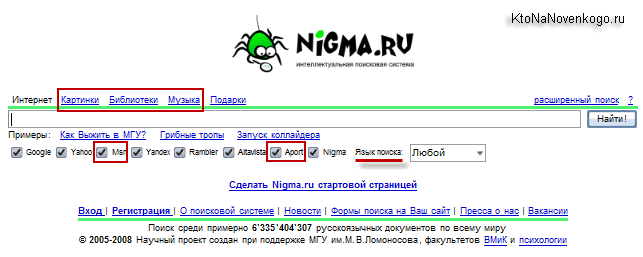
Выглядел он тогда довольно простенько:

Однако, я разделяю их чувство юмора, которое сподвигло сделать подпись «Самая умная поисковая система», ибо тоже иногда на скриншотах запечатлеваю надпись «Самый лучший блог», которая иногда даже вызывает «справедливый» гнев в комментариях.

К сожалению, как мне кажется, время для входа на рынок поиска на тот момент уже было упущено. Основные конкуренты Нигмы к этому времени уже успешно существовали и развивались в течении целого десятилетия. Яндекс окончательно встал на ноги в финансовом плане, а Гугл осуществлял успешную экспансию на рынок поиска рунета.

По началу, кстати, Nigma имела такое преимущество перед Google, как учет русской морфологии, и могла, гипотетически, иметь с этого дивиденды, используя базу Google. Но вскоре лидер мирового поиска сам освоился с русской морфологией и особых козырей в данном аспекте у этой системы уже не стало.

Ее разработчикам пришлось придумывать новые фичи, которыми стали в итоге расширенные подсказки, определение и выделение официальных сайтов, специальные надстройки над поисковой выдачей под названием Нигма математика и химия, а так же отдельный поиск по торрент файлам и музыке.

Последнее несколько диссонирует с классическими поисковиками, которые пытаются всячески дистанцироваться от таких скользких, в смысле защиты копирайта и авторского права, тем. Ибо подоить денег с жирных коров поиска желающих всегда найдется море. Но в нашем случае, скорее всего, срабатывает принцип «неуловимого Джо».

Если идти в хронологическом порядке, то к 2008 году изменяется немного интерфейс и добавляется возможность поиска в Nigma по музыке, книгам (в онлайн библиотеках), а также по картинкам (ну, точнее по словам в атрибуте Alt или стоящими рядом с ними, а не так, как это реализовано при реальном поиске по изображениям от Тинай или Гугла). Кроме этого добавляется возможность использования индексной базы Апорта и Бинга:

Ну, а в 2010 году внешний вид сайта принимает уже привычный вид, за исключение логотипа, где еще используется латинское написание поисковой системы:

Разработкой алгоритмов до сих пор занимаются люди имеющие отношение к МГУ и поэтому понятно и оправдано присутствие в Нигме.ру таких инструментов, как математика и химия. Кстати, довольно-таки прикольные вещи, которые с успехом используют многие школьники и студенты.

Нигма Математика, Химия и Музыка

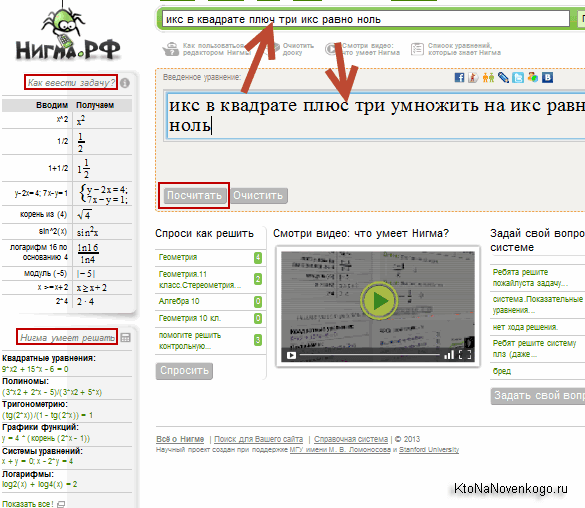
Лично я сейчас вам уже однозначно и не отвечу, с какой стороны можно безопасно подходить к дискриминанту, но мой сын по достоинству оценивает возможность ввода в адресной строке (а сейчас и в специальном разделе «Математика») уравнения или математического выражения и получения не только ответа, но, при желании, и хода решения:

Как видите, я использовал текстовое описание уравнения (кстати, с ошибкой, которая была без вопросов исправлена, т.к. в систему по умолчанию встроен модуль проверки правописания), ибо печатаю я вслепую и довольно быстро, а вот формулу со спецзнаками мне набирать гораздо муторнее.

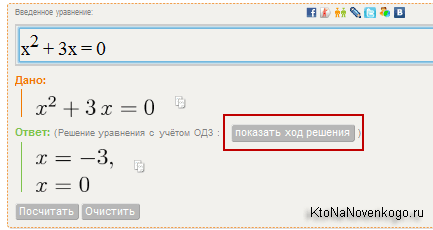
Однако, Nigma-математика без проблем перевела мой текст в формулу, нашла ответ и даже предложила просмотреть ход решения (его скриншот не привожу, ибо оно большое):

Там же вам предложат посмотреть небольшой ролик с экскурсом в математику от интеллектуальной поисковой системы:

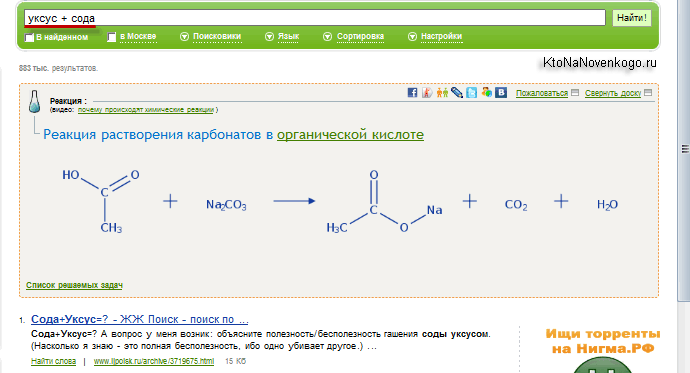
Еще прикольнее для меня выглядит Нигма-химия, ибо ее я тридцать лет назад изучал и полностью позабыл, хотя и давалась она мне тогда очень легко. Есть возможность получать формулы как из неорганической химии, так и частично из органической (где вообще мрак какой-то).

Причем запросы можно тупо вводить текстом, например, так (интересная реакция в желудке может произойти):

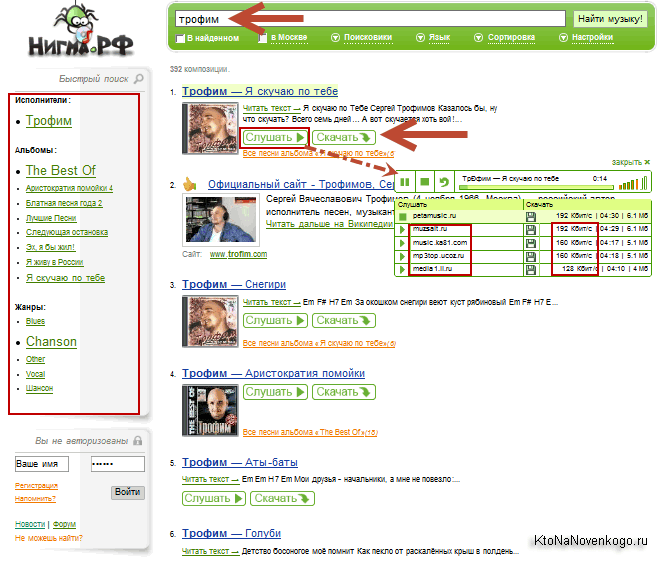
Nigma-музыка тоже не менее прикольна (над формой поиска для нее выделена специальная ссылка «Музыка»), ибо позволяет по запросу найти не только ссылку на песню, но и прослушать ее во встроенном плеере, или даже закачать к себе на компьютер:

При прослушивании вы сможете увидеть адреса сайтов, где данные музыкальные композиции имеют место быть с указанием битрейта и ссылок на скачивание. Кстати, если вы захотите загрузить свои музыкальные файлы, то для этого понадобится пройти регистрацию, форма которой расположена под левой колонкой с фильтрами.

На вопросы про попрание прав правообладателей представители Нигмы отвечают что-то вроде того, что данный поиск по музыкальным файлам, наоборот, поможет этим самым правообладателям отследить тех, кто их права попирает. И в этом есть разумное зерно.

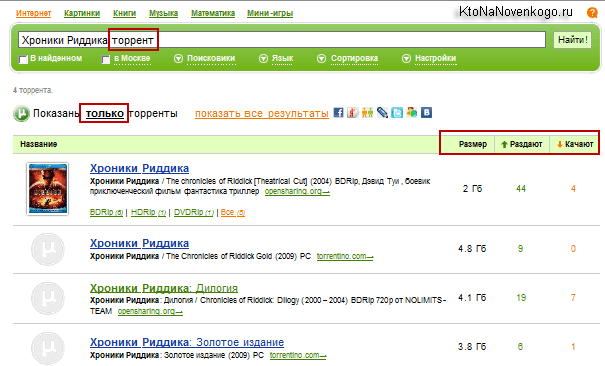
Ну, и понятное дело, что поиск по торрент файла от Nigma поможет уже правообладателям видео и софтовой продукции отследить источники попрания их прав. Почему-то отдельной ссылки для рысканья по торрентам не предусмотрели, но в правом верхнем углу выдачи периодически выскакивает рекламный баннер, призывающий совершенно бесплатно и без регистрации осуществить данный вид поиска.

Хотя, достаточно просто ввести запрос в адресной строке Нигмы и дописать через пробел слово «торрент», что бы получить сводную таблицу всех найденных файлов с указанием их названия, веса, количества пиров и сидов, а так же адреса сайтов, где все это богатство было найдено.

Поисковые подсказки Нигмы.ру и другие особенности

Ну, и еще стоит сказать про немного необычные поисковые подсказки в этой системе. В последнее время мы все привыкли, что поиск сам зачастую знает, что мы хотим у него спросить, и по мере ввода запроса в строке он предлагает свои варианты.

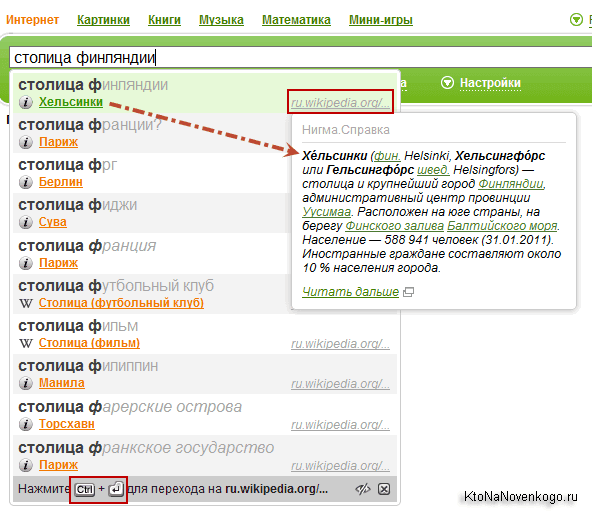
Это удобно, но Nigma пошла еще дальше и в некоторых случаях уже в выпадающем списке подсказок пытается дать краткий или даже развернутый ответ на вводимый вами запрос (а кто же тогда по контекстной рекламе из выдачи будет щелкать, если все поисковики такую же фичу у себя реализуют):

Я набрал в строке запрос «столица ф», после чего мне показали выпадающий список с перечнем всех возможных государств на эту букву с указанием их столиц (краткий ответ), а при подведении курсора мыши к одному из этих кратких ответов, вам покажут более развернутую справку на основе информации, взятой из того, что мы называем Википедией.

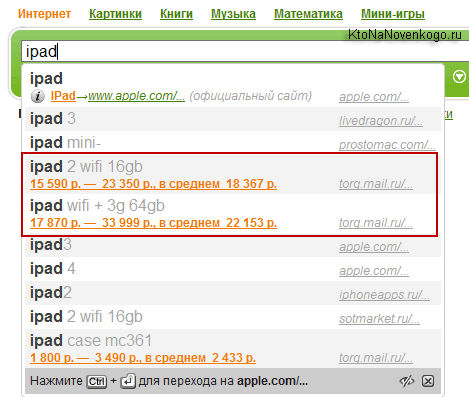
Заметьте, что ответ я получил вообще не нажимая Энтер и не видя выдачи по этому запросу (и рекламу вместе с ней). По-моему, удобно. Иногда так же удобно бывает получать ценовой диапазон по товарным запросам (цены берутся из Товаров Майла):

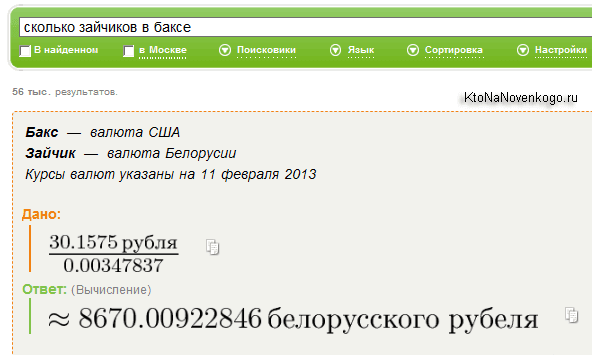
Еще у этого поисковика прикольно работает конвертер различных физический величин, валют и прочей ерунды. Причем, можно все это набирать словами и даже на жаргоне. Собственно, в статьях про то, как искать в Yandex.ru и как гуглить, я упоминал про похожие возможности лидеров рунета.

Как вам такой вариант запроса в Нигме: «сколько зайчиков в баксе». Ну, она говорит, что столько:

Вы знаете, мне довольно часто приходит в голову поискать в интернете расшифровку той или иной встретившейся аббревиатуры, но в выдаче Яндекса или Гугла не всегда это можно увидеть в сниппете и приходится заходить на сайты, искать там и тратить дополнительно время.

На Nigma.ru все реализовано в этом плане несколько более удобно. При вводе аббревиатуры в поисковой строке, можно будет увидеть ее наиболее частую расшифровку в левой колонке с фильтрами, а под спойлером Аббревиатуры можно будет найти более редкие варианты этого сокращения:

Если введенный запрос подразумевает в качестве ответа официальный сайт, то Нигма.рф помечает его в подсказках соответствующей надписью в скобках, а в выдаче перед его заголовком будет красоваться рука с поднятым большим (не средним) пальцем:

Фишечки довольно приятные. К ним бы еще и денежные вливания широкой рекой — вот тогда бы эта поисковая система заиграла совсем другими красками (они, кстати, одно время в контекстной рекламе Директа крутились, но потом Яндекс посчитал, что не гоже пиарить конкурента).

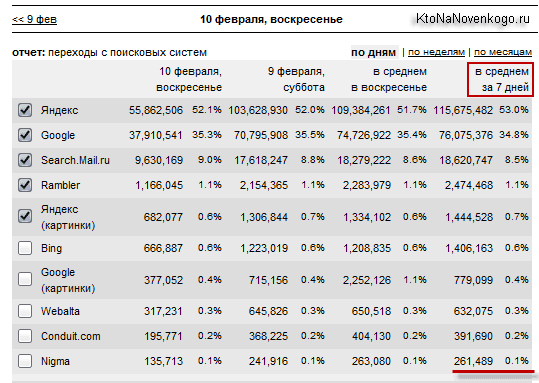
А пока все это по большому счету остается невостребованным, ибо доля Нигмы на поисковом рынке рунета крайне мала (по данным статистики счетчика LI):

Переходов с этого поисковика на сайты в доменной зоне ru в семьдесят раз меньше, чем с не самого популярного Майла. О его посещаемости можно косвенно судить и по показателю Алекса Ранк, но он даже меньше, чем у KtoNaNovenkogo.ru (в рунете этот показатель очень относителен, ибо тулбаров Алексы установлено у пользователей этого сегмента глобальной сети крайне не много) и фактически ни о чем не говорит.

Есть у них в планах выход на рынок поиска Вьетнама, но проект itim.vn до сих пор находится в разработке и доступен только по инвайтам, как уверяют разработчики Nigma. В то время, как начавший примерно в то же самое время экспансию во Вьетнам не безызвестный Ашманов (автор Сайт-аудитора), успешно запустил свой портал Wada.vn.

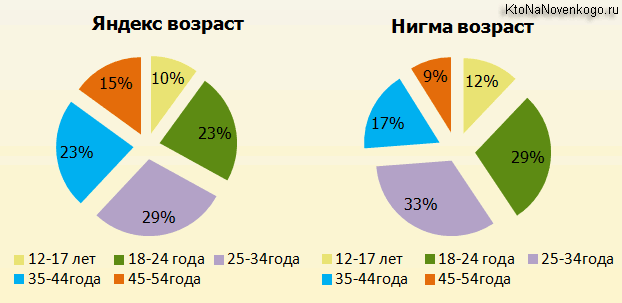
Что касается аудитории, которая присуща этому поисковику, то в силу наличия сервисов Нигма химия, математика и музыка, можно было бы сделать предположение о ее крайне небольшом среднем возрасте. Однако, на конференции РИФ, прошедшей более года назад, выступал представитель этой системы (по-моему, это был Владимир Чернышев) и приводил график ее возрастной аудитории в сравнении с Яндексом:

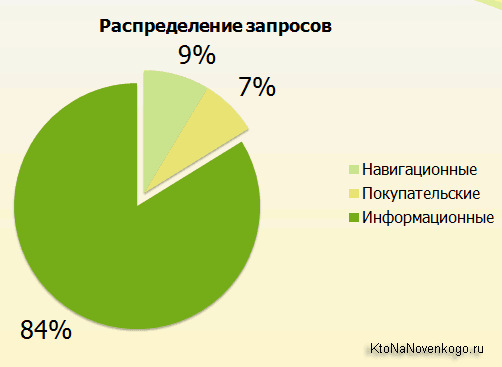
Особых отличий нет, как мы видим. То же самое касается, кстати, и половой принадлежности посетителей (примерно фифти-фифти). Это сравнение было важно для Сеошников, которые могли аппроксимировать изложенные после статистические данные по Nigma на Яндекс или Гугл. В частности приводился процент различных типов запросов к их системе:

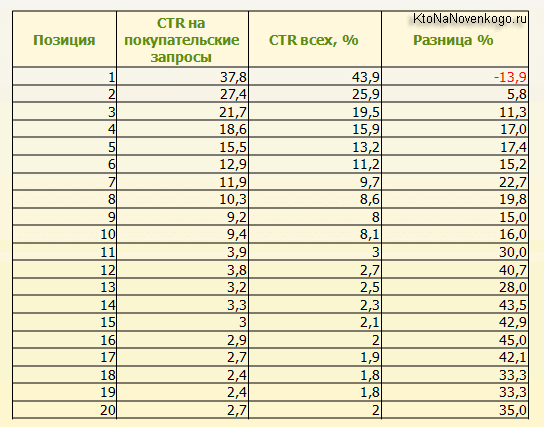
А так же очень любопытные данные по распределению пользовательских предпочтений (CTR) среди первых 20 мест в Топе:

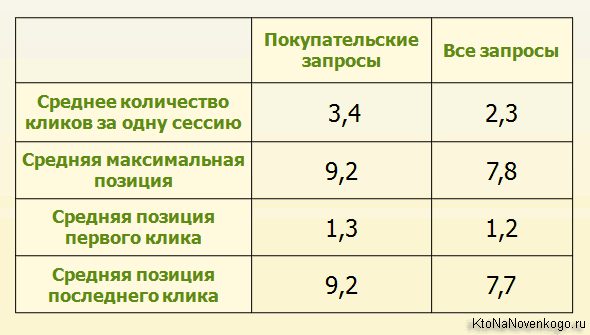
За время одной сессии пользователь часто кликает по разным объявлениям, поэтому любопытно среднее количество таких кликов, а так же диапазон позиций, в пределах которых в среднем эти клики совершаются:

Надеюсь, что кто-то, заинтересовавшись моим описанием, обратит внимание на этот поисковик, однако, в вопросе выбора «поиска по-умолчанию» зачастую первостепенную роль играют привычка и наличие мелочей, к которым прикипел. Ну, вот я, например, не могу пользоваться Гуглом из-за того, что там фавиконы сайтов не показываются.

Пустячок, а вот привык я совершать переходы по знакомым сайтам, которые легко в Яндексе могу узнавать по фавиконам и хоть ты тресни.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Комментарии и отзывы (10)

Заметил, что в приветствии в начале статьи последнее время ссылка на главную в «KtoNaNovenkogo.ru» — отсутствует, а перенесена в конец статьи. Это результат каких то наблюдений и соответствующих выводов или просто различные варианты ссылки на главную?

Нигма — огонь. жалко, что её не было, когда я в школе учился. и в универе. блин.

Приветствую. Хотелось бы что бы даный проект ширился и развивался, но боюсь если за ним не станет какой-либо большой дядя с гаспрома быть ему влитым в какой-нибудь маил или яндекс.

Кстати в хроме есть расширение, решающие проблему отображения фавиконов.

Я вообще заметил что перелинковка осталась кроме ссылки на главную, потому что при совещании у яши они намекали что в минус пойдёт если с каждой страницы сайта будет линк на главную.

опять в три часа ночи не могу уйти с блога;)

Года с три точно его использую при поиске.

Единственное, что иногда для особых целей приходится гуглом искать или яндексом, но в порядке исключения!

Увы во время учебы в школе и в вузе не было ещё такого функционала как в нигме

Пользуюсь со времени его появления на свет. Считаю его неизмеримо лучшим по сравнению с многими другими — Яндексом и, конечно, Гуглом или Мейлом, по выдаче результатов поиска и особенно их представлению. Идея кластеризации гениальна. Хороши мелкие фичи его. Лучший поисковик среди русских и иностранных (на английском, французском, немецком языках).7

Нигма — система поиска хорошая, одна из лучших, но для научных расчётов и поиска по библиотекам. Основная же — гугл.

Поиск очень хороший есть только три недостатка

1.Поиск для андроида только через гугл плей маркет а так только виджет

2.На большенстве браузеров его нет и во многих случаях не установить как скажем в UC для андроид или в опера 40 и выше для windows

и3. Слишком часто по непонятным причинам блокирует с предложением ввести капчу

Вот если с этим справятся то думаю обгонят конкурентов особенно гугла

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Вспомогательная страница к разделу ☞ ИНТЕРПОЛЯЦИЯ.

Метод наименьших квадратов

Пусть из физических соображений можно считать (предполагать), что величины $ x_<> $ и $ y_<> $ связаны линейной зависимостью вида $ y=kx+b $, а неизвестные коэффициенты $ k_<> $ и $ b_<> $ должны быть оценены экспериментально. Экспериментальные данные представляют собой $ m>1 $ точек на координатной плоскости $ (x_1,y_1), \dots, (x_m,y_m) $. Если бы эти опыты производились без погрешностей, то подстановка данных в уравнение приводила бы нас к системе из $ m_<> $ линейных уравнений для двух неизвестных $ k_<> $ и $ b_<> $: $$ y_1=k\,x_1+b, \dots, y_m=k\,x_m+b \ . $$ Из любой пары уравнений этой системы можно было бы однозначно определить коэффициенты $ k_<> $ и $ b_<> $.

Однако, в реальной жизни опытов без погрешностей не бывает

Дорогая редакция! Формулировку закона Ома следует уточнить следующим образом:«Если использовать тщательно отобранные и безупречно подготовленные исходные материалы, то при наличии некоторого навыка из них можно сконструировать электрическую цепь, для которой измерения отношения тока к напряжению, даже если они проводятся в течение ограниченного времени, дают значения, которые после введения соответствующих поправок оказываются равными постоянной величине».

Источник: А.М.Б.Розен. Физики шутят. М.Мир.1993.

Будем предполагать, что величины $ x_<1>,\dots,x_m $ известны точно, а им соответствующие $ y_1,\dots,y_m $ — приближенно. Если $ m>2 $, то при любых различных $ x_ $ и $ x_j $ пара точек $ (x_,y_i) $ и $ (x_,y_j) $ определяет прямую. Но другая пара точек определяет другую прямую, и у нас нет оснований выбрать какую-нибудь одну из всех прямых.

Часто в задаче удаленность точки от прямой измеряют не расстоянием, а разностью ординат $ k\,x_i+b-y_i $, и выбирают прямую так, чтобы сумма квадратов всех таких разностей была минимальна. Коэффициенты $ k_0 $ и $ b_ <0>$ уравнения этой прямой дают некоторое решение стоящей перед нами задачи, которое отнюдь не является решением системы линейных уравнений $$ k\,x_1+b=y_1,\dots, k\,x_+b=y_m $$ (вообще говоря, несовместной).

Рассмотрим теперь обобщение предложенной задачи. Пусть искомая зависимость между величинами $ y_<> $ и $ x_<> $ полиномиальная: $$ y_1=f(x_1),\dots , y_m=f(x_m), \quad npu \quad f(x)=a_0+a_1x+\dots+a_x^ $$ Величина $ \varepsilon_i=f(x_i)-y_i $ называется $ i_<> $-й невязкой 1) . Уравнения $$ \left\<\begin a_0+a_1x_1+\dots+a_x_1^&=&y_1, \\ a_0+a_1x_2+\dots+a_x_2^&=&y_2, \\ \dots & & \dots \\ a_0+a_1x_m+\dots+a_x_m^&=&y_m \end \right. $$ называются условными. Матрица этой системы — матрица Вандермонда (она не обязательно квадратная).

Предположим что данные интерполяционной таблицы $$ \begin x & x_1 & x_2 & \dots & x_m \\ \hline y & y_1 & y_2 &\dots & y_m \end $$ не являются достоверными: величины $ x_<> $ нам известны практически без искажений (т.е. на входе процесса мы имеем абсолютно достоверные данные), а вот измерения величины $ y_<> $ подвержены случайным (несистематическим) погрешностям.

Задача. Построить полином $ f_<>(x) $ такой, чтобы величина $$ \sum_^m [f(x_j)-y_j]^2 $$ стала минимальной. Решение задачи в такой постановке известно как метод наименьшик квадратов 2) .

В случае $ \deg f_<> =m-1 $ мы возвращаемся к задаче интерполяции в ее классической постановке. Практический интерес, однако, представляет случай $ \deg f_<> n $: $$S=\left(\begin 1 &1&1&\ldots&1\\ x_1 &x_2&x_3&\ldots&x_\\ \vdots&& & &\vdots\\ x_1^ &x_2^&x_3^&\ldots&x_m^ \end\right) \cdot \left(\begin 1 &x_1&x_1^2&\ldots&x_1^\\ 1 &x_2&x_2^2&\ldots&x_2^\\ \ldots&& & &\ldots\\ 1 &x_m&x_m^2&\ldots&x_m^ \end\right)$$ $$\det S = \sum_<1\le j_1 0 $. По теореме Крамера система нормальных уравнений имеет единственное решение.

Осталось недоказанным утверждение, что полученное решение доставляет именно минимум сумме квадратов невязок. Этот факт следует из доказательства более общего утверждения — о псевдорешении системы линейных уравнений. Этот результат приводится ☟ НИЖЕ. ♦

Собственно минимальное значение величины cуммы квадратов невязок, а точнее усреднение по количеству узлов $$ \sigma=\frac<1>\sum_^m (f(x_j) -y_j)^2 $$ называется среднеквадратичным отклонением.

Показать, что линейный полином $ y=a_<0>+a_1x $, построенный по методу наименьших квадратов, определяет на плоскости $ (x_<>,y) $ прямую, проходящую через центроид

Пример. По методу наименьших квадратов построить уравнение прямой, аппроксимирующей множество точек плоскости, заданных координатами из таблицы

$$ \begin x & 0.5 & 1 & 1.5 & 2 & 2.5 & 3 \\ \hline y & 0.35 & 0.80 & 1.70 & 1.85 & 3.51 & 1.02 \end $$

Решение. Имеем $$ s_0=6, s_1=0.5 + 1 + 1.5 + 2 + 2.5 + 3=10.5, $$ $$ s_2=0.5^2 + 1^2 + 1.5^2 + 2^2 + 2.5^2 + 3^2=22.75, $$ $$t_0=0.35 + 0.80 + 1.70 + 1.85 + 3.51 + 1.02=9.23, $$ $$ t_1 =0.5\cdot 0.35 + 1 \cdot 0.80 + 1.5 \cdot 1.70 + 2 \cdot 1.85 + $$ $$ +2.5 \cdot 3.51 + 3 \cdot 1.02=19.06 . $$ Решаем систему нормальных уравнений $$ \left( \begin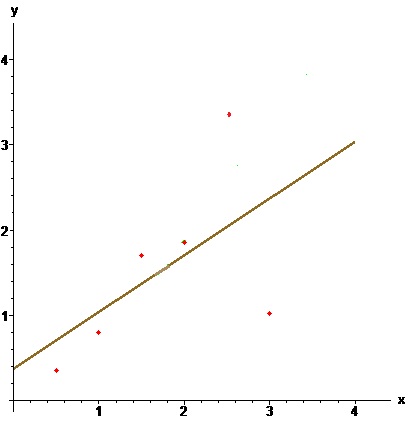 6 & 10.5 \\ 10.5 & 22.75 \end \right) \left( \begin a_0 \\ a_1 \end \right)= \left( \begin 9.23 \\ 19.06 \end \right), $$ получаем уравнение прямой в виде $$ y= 0.375 + 0.665\, x\ .$$

Вычислим и полиномы более высоких степеней. $$ f_2(x)=-1.568+3.579\, x-0.833\,x^2 \ , $$ $$ f_3(x)=2.217-5.942\,x+5.475\,x^2-1.201\, x^3 \ , $$ $$ f_4(x)= -4.473+17.101\,x-19.320\,x^2+9.205\, x^3-1.487\,x^4 \ , $$ $$ f_5(x)= 16.390-71.235\,x+111.233\,x^2-77.620\,x^3+25.067\,x^4-3.0347\, x^5 . $$

Среднеквадратичные отклонения: $$ \begin \deg & 1 & 2 & 3 & 4 & 5 \\ \hline \sigma & 0.717 & 0.448 & 0.204 &0.086 & 0 \end $$ ♦

Возникает естественный вопрос: полином какой степени следует разыскивать в МНК? При увеличении степени точность приближения, очевидно, увеличивается. Вместе с тем, увеличивается сложность решения системы нормальных уравнений и даже при небольших степенях $ n $ (меньших $ 10 $) мы столкнемся с проблемой чувствительности решения к точности представления входных данных.

Влияние систематических ошибок

Пример. Уравнение прямой, аппроксимирующей множество точек плоскости, заданных координатами из таблицы

$$ \begin x & 0.5 & 1 & 1.5 & 2 & 2.5 & 3 \\ \hline y & 0.35 & 0.80 & 1.70 & 1.85 & 2.51 & 2.02 \end $$ имеет вид (охра) $$ y=0.175+0.779\, x \, . $$ Теперь заменим значение $ y_5 $ на $ 0.2 $. Уравнение прямой принимает вид: $$ y=0.483+0.383\, x \, . $$ График (зеленый) существенно изменился. Почему это произошло? — Дело в том, что эффективность метода наименьших квадратов зависит от нескольких предположений относительно входных данных: в нашем случае — значений $ y $. Предполагается, что эти величины являлись результатами экспериментов, измерений, и, если они подвержены погрешностям, то эти погрешности носят характер несистематических флуктуаций вокруг истинных значений. Иными словами, изначально предполагается, что в действительности точки плоскости должны лежать на некоторой прямой. И только несовершенство наших методов измерений (наблюдений) демонстрирует смещение их с этой прямой. Ответ для исходной таблицы визуально подтвержает это предположение: экспериментальные точки концентрируются вокруг полученной прямой и величины невязок (отклонений по $ y $-координате) имеют «паритет» по знакам: примерно половина точек лежит выше прямой, а половина — ниже.

После замены значения $ y_5 $ на новое, значительно отличающееся от исходного, существенно меняется величина $ 5 $-й невязки $ \varepsilon_5= ax_5+b-y_5 $. А поскольку в минимизируемую функцию эта невязка входи еще и в квадрате, то понятно, что изначальная прямая просто не в состоянии правильно приблизить новую точку.

Эта проблема становится актуальной в тех случаях, когда в «истинно случайный» процесс привносятся намеренные коррективы. Данные начинают подвергаться существенным искажениям, возможно, даже имеющим «злой» умысел 3) .

Как бороться с ошибками такого типа? Понятно, что решение возможно в предположении, что число таких — систематических — ошибок должно быть существенно меньшим общего количества экспериментальных данных. Понятно, что каким-то образом эти «выбросы» надо будет исключить из рассмотрения, т.е. очистить «сырые» данные от «мусора» — прежде чем подсовывать их в метод наименьших квадратов (см. ☞ цитату). Как это сделать?

Псевдорешение системы линейных уравнений

Рассмотрим теперь обобщение задачи предыдущего пункта. В практических задачах часто бывает нужно найти решение, удовлетворяющее большому числу возможно противоречивых требований. Если такая задача сводится к системе линейных уравнений $$ \left\<\begin a_<11>x_1 +a_<12>x_2+\ldots+a_<1n>x_n &=&b_1\\ a_<21>x_1 +a_<22>x_2+\ldots+a_<2n>x_n &=&b_2\\ \ldots& & \ldots \\ a_x_1 +a_x_2+\ldots+a_x_n &=&b_m \end\right. \iff AX= <\mathcal B>$$ при числе уравнений $ m_<> $ большем числа неизвестных $ n_<> $, то такая переопределенная система, как правило, несовместна. В этом случае задача может быть решена только путем выбора некоторого компромисса — все требования могут быть удовлетворены не полностью, а лишь до некоторой степени.

Псевдорешением системы $ AX= <\mathcal B>$ называется столбец $ X\in \mathbb R^n $, обеспечивающий минимум величины $$ \sum_^m [a_x_1 +a_x_2+\ldots+a_x_n-b_i]^2 \ . $$

Теорема. Существует псевдорешение системы

$$ AX= <\mathcal B>$$ и оно является решением системы $$ \left[A^<\top>A \right]X=A^ <\top> <\mathcal B>\ . $$ Это решение будет единственным тогда и только тогда, когда $ \operatorname A =n $.

Система $ \left[A^<\top>A \right]X=A^ <\top> <\mathcal B>$ называется нормальной системой по отношению к системе $ AX= <\mathcal B>$. Формально она получается домножением системы $ AX= <\mathcal B>$ слева на матрицу $ A^ <\top>$. Заметим также, что если $ m=n_<> $ и $ \det A \ne 0 $, то псевдорешение системы совпадает с решением в традиционном смысле.

Доказательство ☞ ЗДЕСЬ.

Если нормальная система имеет бесконечное количество решений, то обычно в качестве псевдорешения берут какое-то одно из них — как правило то, у которого минимальна сумма квадратов компонент («длина»).

Пример. Найти псевдорешение системы

$$x_1+x_2 = 2, \ x_1-x_2 = 0,\ 2\, x_1+x_2 = 2 \ .$$

Решение. Имеем: $$A=\left( \begin 1 & 1 \\ 1 & -1 \\ 2 & 1 \end \right),\ \operatorname A =2,\ <\mathcal B>= \left( \begin 2 \\ 0 \\ 2 \end \right), \ A^<\top>A= \left( \begin 6 & 2 \\ 2 & 3 \end \right), \ A^ <\top> <\mathcal B>= \left( \begin 6 \\ 4 \end \right). $$

Ответ. $ x_1=5/7, x_2 = 6/7 $.

Показать, что матрица $ A^<\top>A $ всегда симметрична.

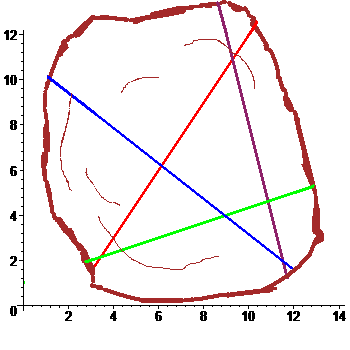
На дубовой колоде лежит мелкая монетка. К колоде

по очереди подходят четыре рыцаря и каждый наносит удар мечом, стараясь попасть по монетке. Все промахиваются. Расстроенные, рыцари уходят в харчевню пропивать злосчастную монетку. Укажите максимально правдоподобное ее расположение, имея перед глазами зарубки: $$ \begin 3\, x &- 2\, y&=& 6,\\ x &-3\,y&=&-3,\\ 11\,x& + 14\,y&=& 154, \\ 4\,x&+y&=&48. \end $$

Геометрическая интерпретация

Псевдообратная матрица

Пусть сначала матрица $ A_<> $ порядка $ m\times n_<> $ — вещественная и $ m \ge n_<> $ (число строк не меньше числа столбцов). Если $ \operatorname (A) = n $ (столбцы матрицы линейно независимы), то псевдообратная к матрице $ A_<> $ определяется как матрица $$ A^<+>=(A^<\top>A)^ <-1>A^ <\top>\ . $$ Эта матрица имеет порядок $ n \times m_<> $. Матрица $ (A^<\top>A)^ <-1>$ существует ввиду того факта, что при условии $ \operatorname (A) = n $ будет выполнено $ \det (A^ <\top>A) > 0 $ (см. упражнение в пункте ☞ ТЕОРЕМА БИНЕ-КОШИ или же пункт ☞ СВОЙСТВА ОПРЕДЕЛИТЕЛЯ ГРАМА ). Очевидно, что $ A^ <+>\cdot A = E_ $, т.е. псевдообратная матрица является левой обратной для матрицы $ A_<> $. В случае $ m=n_<> $ псевдообратная матрица совпадает с обратной матрицей: $ A^<+>=A^ <-1>$.

Пример. Найти псевдообратную матрицу к матрице $$ A= \left( \begin 1 & 0 \\ 0 & 1 \\ 1 & 1 \end \right) \ . $$

Решение. $$ A^<\top>= \left( \begin 1 & 0 & 1 \\ 0 & 1 & 1 \end \right) \ \Rightarrow \ A^ <\top>\cdot A = \left( \begin 2 & 1 \\ 1 & 2 \end \right) \ \Rightarrow $$ $$ \Rightarrow \ (A^ <\top>\cdot A)^ <-1>= \left( \begin 2/3 & -1/3 \\ -1/3 & 2/3 \end \right) \ \Rightarrow $$ $$ \Rightarrow \quad A^ <+>= (A^ <\top>\cdot A)^ <-1>A^ <\top>= \left( \begin 2/3 & -1/3 & 1/3 \\ -1/3 & 2/3 & 1/3 \end \right) \ . $$ При этом $$ A^ <+>\cdot A = \left( \begin 1 & 0 \\ 0 & 1 \end \right),\quad A \cdot A^ <+>= \left( \begin 2/3 & -1/3 & 1/3 \\ -1/3 & 2/3 & 1/3 \\ 1/3 & 1/3 & 2/3 \end \right) \ , $$ т.е. матрица $ A^ <+>$ не будет правой обратной для матрицы $ A_<> $. ♦

Вычислить псевдообратную матрицу для $$ \mathbf\ \left( \begin 1 & 0 \\ 1 & 1 \\ 1 & 1 \end \right) \quad ; \quad \mathbf\ \left( \begin x_1 \\ x_2 \\ x_3 \end \right) \ . $$

Концепция псевдообратной матрицы естественным образом возникает из понятия псевдорешения системы линейных уравнений . Если $ A^ <+>$ существует, то псевдорешение (как правило, переопределенной и несовместной!) системы уравнений $ AX=\mathcal B_<> $ находится по формуле $ X= A^ <+>\mathcal B $ при любом столбце $ \mathcal B_<> $. Верно и обратное: если $ E_<[1]>, E_<[2]>,\dots, E_ <[m]>$ – столбцы единичной матрицы $ E_m $: $$ E_<[1]>=\left( \begin 1 \\ 0 \\ 0 \\ \vdots \\ 0 \end \right),\ E_<[2]>=\left( \begin 0 \\ 1 \\ 0 \\ \vdots \\ 0 \end \right),\dots, E_<[m]>=\left( \begin 0 \\ 0 \\ 0 \\ \vdots \\ 1 \end \right),\ $$ а псевдорешение системы уравнений $ AX=E_ <[j]>$ обозначить $ X_ $ (оно существует и единственно при условии $ \operatorname (A) = n $), то $$ A^<+>=\left[X_1,X_2,\dots,X_m \right] \ . $$

Теорема. Пусть $ A_<> $ вещественная матрица порядка $ m\times n_<> $, $ m \ge n_<> $ и $ \operatorname (A) = n $. Тогда псевдообратная матрица $ A^ <+>$ является решением задачи минимизации

$$ \min_> \|AX-E_m\|^2 $$ где минимум разыскивается по всем вещественным матрицам $ X_<> $ порядка $ n\times m_<> $, а $ || \cdot || $ означает евклидову норму матрицы (норму Фробениуса) : $$ \|[h_]_\|^2=\sum_ h_^2 \ . $$ При сделанных предположениях решение задачи единственно.

С учетом этого результата понятно как распространить понятие псевдообратной матрицы на случай вещественной матрицы $ A_^<> $, у которой число строк меньше числа столбцов: $ m ☞ ЗДЕСЬ

Источники

[1]. Беклемишев Д.В. Дополнительные главы линейной алгебры. М.Наука.1983, с.187-234

Системы с нелинейными уравнениями

Нелинейные уравнения с двумя неизвестными

Системы из двух уравнений, одно из которых линейное

Однородные уравнения второй степени с двумя неизвестными

Системы из двух уравнений, одно из которых однородное

Системы из двух уравнений, сводящиеся к системам, в которых одно из уравнений однородное

Примеры решения систем уравнений других видов

Нелинейные уравнения с двумя неизвестными

Определение 1 . Пусть A – некоторое множество пар чисел (x ; y) . Говорят, что на множестве A задана числовая функция z от двух переменных x и y , если указано правило, с помощью которого каждой паре чисел из множества A ставится в соответствие некоторое число.

Задание числовой функции z от двух переменных x и y часто обозначают так:

причем в записи (1) числа x и y называют аргументами функции , а число z – значением функции , соответствующим паре аргументов (x ; y) .

Определение 2 . Нелинейным уравнением с двумя неизвестными x и y называют уравнение вида

где f (x , y) – любая функция, отличная от функции

где a , b , c – заданные числа.

Определение 3 . Решением уравнения (2) называют пару чисел (x ; y) , для которых формула (2) является верным равенством.

Пример 1 . Решить уравнение

Решение . Преобразуем левую часть уравнения (3):

Таким образом, уравнение (3) можно переписать в виде

Поскольку квадрат любого числа неотрицателен, то из формулы (4) вытекает, что неизвестные x и y удовлетворяют системе уравнений

решением которой служит пара чисел (6 ; 3) .

Пример 2 . Решить уравнение

вытекает, что уравнение (5) решений не имеет.

Ответ : Решений нет.

Пример 3 . Решить уравнение

Следовательно, решением уравнения (6) является бесконечное множество пар чисел вида

где y – любое число.

Системы из двух уравнений, одно из которых линейное

Определение 4 . Решением системы уравнений

называют пару чисел (x ; y) , при подстановке которых в каждое из уравнений этой системы получается верное равенство.

Системы из двух уравнений, одно из которых линейное, имеют вид

где a , b , c – заданные числа, а g(x , y) – функция двух переменных x и y .

Пример 4 . Решить систему уравнений

(7)

Решение . Выразим из первого уравнения системы (7) неизвестное y через неизвестное x и подставим полученное выражение во второе уравнение системы:

Таким образом, решениями системы (7) являются две пары чисел

и

Ответ : (– 1 ; 9) , (9 ; – 1)

Однородные уравнения второй степени с двумя неизвестными

Определение 5 . Однородным уравнением второй степени с двумя неизвестными x и y называют уравнение вида

где a , b , c – заданные числа.

Пример 5 . Решить уравнение

Решение . Для каждого значения y рассмотрим уравнение (8) как квадратное уравнение относительно неизвестного x . Тогда дискриминант D квадратного уравнения (8) будет выражаться по формуле

откуда с помощью формулы для корней квадратного уравнения найдем корни уравнения (8):

Ответ . Решениями уравнения (8) являются все пары чисел вида

( y ; y) или

где y – любое число.

Следствие . Левую часть уравнения (8) можно разложить на множители

Системы из двух уравнений, одно из которых однородное

Системы из двух уравнений, одно из которых однородное, имеют вид

где a , b , c – заданные числа, а g(x , y) – функция двух переменных x и y .

Пример 6 . Решить систему уравнений

(9)

рассматривая его как квадратное уравнение относительно неизвестного x :

.

В случае, когда x = – y , из второго уравнения системы (9) получаем уравнение

корнями которого служат числа y₁ = 2 , y₂ = – 2 . Находя для каждого из этих значений y соответствующее ему значение x , получаем два решения системы: (– 2 ; 2) , (2 ; – 2) .

,

из второго уравнения системы (9) получаем уравнение

которое корней не имеет.

Ответ : (– 2 ; 2) , (2 ; – 2)

Системы из двух уравнений, сводящиеся к системам, в которых одно из уравнений однородное

Пример 7 . Решить систему уравнений

(10)

Решение . Совершим над системой (10) следующие преобразования:

• второе уравнение системы оставим без изменений;
• к первому уравнению, умноженному на 5 , прибавим второе уравнение, умноженное на 3 , и запишем полученный результат вместо первого уравнения системы (10).

В результате система (10) преобразуется в равносильную ей систему (11), в которой первое уравнение является однородным уравнением:

(11)

рассматривая его как квадратное уравнение относительно неизвестного x :

.

В случае, когда x = – 5y , из второго уравнения системы (11) получаем уравнение

которое корней не имеет.

,

из второго уравнения системы (11) получаем уравнение

,

корнями которого служат числа y₁ = 3 , y₂ = – 3 . Находя для каждого из этих значений y соответствующее ему значение x , получаем два решения системы: (– 2 ; 3) , (2 ; – 3) .

Ответ : (– 2 ; 3) , (2 ; – 3)

Примеры решения систем уравнений других видов

Пример 8 . Решить систему уравнений (МФТИ)

Решение . Введем новые неизвестные u и v , которые выражаются через x и y по формулам:

(13)

Для того, чтобы переписать систему (12) через новые неизвестные, выразим сначала неизвестные x и y через u и v . Из системы (13) следует, что

(14)

Решим линейную систему (14), исключив из второго уравнения этой системы переменную x . С этой целью совершим над системой (14) следующие преобразования:

• первое уравнение системы оставим без изменений;
• из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.

В результате система (14) преобразуется в равносильную ей систему

из которой находим

(15)

Воспользовавшись формулами (13) и (15), перепишем исходную систему (12) в виде

(16)

У системы (16) первое уравнение – линейное, поэтому мы можем выразить из него неизвестное u через неизвестное v и подставить это выражение во второе уравнение системы:

Следовательно, решениями системы (16) являются две пары чисел

Из формул (13) вытекает, что , поэтому первое решение должно быть отброшено. В случае u₂ = 5, v₂ = 2 из формул (15) находим значения x и y :

Определение 6 . Решением системы из двух уравнений с тремя неизвестными называют тройку чисел (x ; y ; z) , при подстановке которых в каждое уравнение системы получается верное равенство.

Пример 9 . Решить систему из двух уравнений с тремя неизвестными

(17)

Решение . У системы (17) первое уравнение – линейное, поэтому мы можем выразить из него неизвестное z через неизвестные x и y и подставить это выражение во второе уравнение системы:

(18)

Перепишем второе уравнение системы (18) в другом виде:

Поскольку квадрат любого числа неотрицателен, то выполнение последнего равенства возможно лишь в случае x = 4, y = 4 .

Ответ : (4 ; 4 ; – 4)

Замечание . Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы линейных уравнений» и нашим учебным пособием «Системы уравнений».