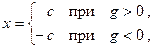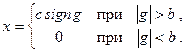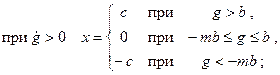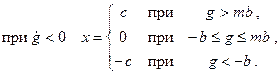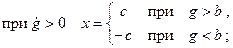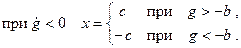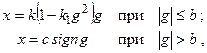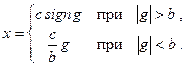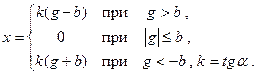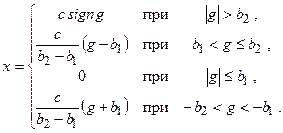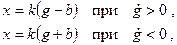Системы с нелинейными элементами в дифференциальных уравнениях

Нелинейные дифференциальные уравнения и системы со специальными свойствами решений Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы —

Изложены результаты исследований, касающиеся построения и исследования аналитических свойств решений нелинейных дифференциальных уравнений и систем (обыкновенных и в частных производных) специального вида.

Похожие темы научных работ по математике , автор научной работы —

NONLINEAR DIFFERENTIAL EQUATIONS AND SYSTEMS WITH SPECIAL PROPERTIES OF SOLUTIONS

The results concerning the construction and research of analytic properties of solutions to nonlinear (ordinary and partial) differential equations and systems of special type are presented.

Текст научной работы на тему «Нелинейные дифференциальные уравнения и системы со специальными свойствами решений»

НЕЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И СИСТЕМЫ СО СПЕЦИАЛЬНЫМИ СВОЙСТВАМИ РЕШЕНИЙ

Белорусский государственный университет информатики и радиоэлектроники П. Бровки, 6, Минск, 220013, Беларусь

Поступила в редакцию 23 января 2014

Изложены результаты исследований, касающиеся построения и исследования аналитических свойств решений нелинейных дифференциальных уравнений и систем (обыкновенных и в частных производных) специального вида.

Ключевые слова: уравнения Пенлеве, гамильтониан, модели случайно-матричного типа, автомодельное решение, системы с хаотическим поведением.

В настоящее время общепризнанным является тот факт, что неприводимые уравнения Пенлеве, полученные французским математиком Пенлеве и его коллегами в начале XX века, играют роль нелинейных аналогов для классических специальных функций. Основное свойство уравнений Пенлеве состоит в том, что их общие решения не имеют подвижных критических особых точек. Данное свойство часто называют Р-свойством, а уравнения с Р-свойством решений — уравнениями Пенлеве-типа или Р-типа. В связи с тем, что отмеченное свойство является в определенном смысле критерием интегрируемости, исключительно актуальной на протяжении трех последних десятилетий является задача построения и исследования аналитических свойств решений нелинейных уравнений и систем высших порядков с Р-свойством решений. Указанные уравнения и системы называют аналогами уравнений Пенлеве высших порядков или высшими аналогами уравнений Пенлеве. Высшие аналоги уравнений Пенлеве (как и сами уравнения Пенлеве) имеют весьма широкий спектр приложений, причем некоторые из них являются автомодельными редукциями хорошо известных высших аналогов нелинейных уравнений в частных производных, таких как Кортевега-де Фриза, Кодри-Додда-Гибона, Каупа-Купершмидта и др.

В данной работе излагаются некоторые результаты, полученные автором за последние пять лет и связанные с: 1) построением нелинейных систем обыкновенных дифференциальных уравнений (ОДУ) второго порядка и выше специального вида и исследованием аналитических свойств их решений; 2) исследованием аналитических свойств решений систем нелинейных ОДУ (связанных, в частности, с моделями случайно-матричного типа) на предмет принадлежности их к системам Р-типа; 3) построением точных автомодельных редукций систем нелинейных уравнений в частных производных (имеющих конкретные приложения) к системам ОДУ с Р-свойством решений.

Результаты предыдущих исследований автора по указанной тематике (начиная с 1983 г.) отражены в публикациях 24.

Преобразования Беклунда уравнений для полиномиальных гамильтонианов, ассоциированных со вторым и четвертым уравнениями Пенлеве

В работах [34] построены системы дифференциальных уравнений

ш» = уш’ — — а, у» = шу’ — уу’ — Ь; (1)

ш’у’ — 2а(у — ш)2 — (у2 — ш2) = в, ш’ + у’ + — у) + (ш — у)2 = 0, (2)

где ш, у — неизвестные функции независимой переменной г; а, Ь, а, в — произвольные постоянные параметры.

Показано, что система (1) является системой Пенлеве-типа, причем она может быть преобразована к виду

ш»2 = —2ш’3 — 2(а + Ь)ш’2 + 2(а + + а2, (3)

у»2 = —2у’3 — 2(а + Ь)у’2 + 2(а + Ь)уу’ + Ь2. (4)

Без ограничения общности можно считать а + Ь = 1, причем а = а — г — — , г2 = 1, а ■

произвольный параметр. Тогда уравнение (3) принимает вид

ш»2 = —2ш’3 — 2гш’2 + + (а — |)2. (5)

Уравнению (5) удовлетворяет функция = 2Я(г, и(г), Г(г)), где

Н(г, и, Г) = ^т + г + |) и — (а — |) — гамильтониан, ассоциированный со вторым уравнением Пенлеве

Г’ = 2Г3 + гГ + а. (Р2)

Для уравнения (5) построено преобразование Беклунда, а также получены нелинейные алгебраические соотношения, связывающие решения уравнения (5) при различных значениях параметра а.

С помощью преобразования У = = —— относительно новых неизвестных

функций и, V система (2) принимает вид

1 (и ‘2 — г’2) — 2а^2 + иг = и’ + + V2 = 0. (6)

Показано, что решения системы (6) выражаются через решения четвертого уравнения Пенлеве

=1_ + 1у3 + 42У2 + 2(22 —2а)+в. (Р4)

На основании этого доказана

Теорема 1. Система (2) является системой Пенлеве-типа. Показано, что функции ш, у удовлетворяют уравнениям

ш»2 — 4(ш — гш’)2 + 2(ш’ + 2а + 1)(2ш’2 + в) = 0, (7)

У2 — 4(у — гу’)2 + 2(у ‘ + 2а — 1)(2у’2 + в) = 0 (8)

Отметим, что по аналогии с уравнением (Р2) уравнение (7) есть уравнение для

полиномиального гамильтониана, ассоциированного с уравнением (Р4). Уравнение (8) получается из (7) преобразованием ш^у, а^а — 1.

Неполиномиальные гамильтонианы, ассоциированные с третьим и пятым

В последние три десятилетия наблюдается значительный интерес к исследованию определенных классов непрерывных и дискретных вероятностных моделей, известных под названием «модели случайно-матричного типа». Источники таких моделей весьма разнообразны.

Одной из наиболее важных характеристик указанных моделей является «нуль вероятность» — вероятность отсутствия частиц в заданном интервале или объединении

интервалов. Нуль вероятности, как правило, могут быть представлены в виде определителей Фредгольма det(1 — |о, где К — есть некоторый интегральный оператор с ядром специального вида, а 0 — множество, где не должно быть частиц. Единственный известный на настоящий момент способ вычисления таких определителей состоит в их характеризации как решений некоторого однородного дифференциального уравнения (ОДУ) или системы уравнений с частными производными.

Известно, что однопараметрическое семейство решений уравнения

Н—-— = — sh2ф + 2a0z 1 • sh ф (а0 — параметр),

являющегося частным случаем уравнения

zww» = zw’2 — ww’ + aw3 + ^w + yzw4 + 5z, (P3)

выражается в терминах определителей Фредгольма специального типа. В работах E. Barouch, B.M. Mc Coy, C.A.Tracy, T.T. Wu, посвященных решению классической проблемы вычисления спиновых корреляционных функций двумерной модели Изинга, был установлен следующий результат: скейлинговый предел двухточечной корреляционной функции модели Изинга допускает замкнутое выражение через решение уравнения (P3) при а=р = 0,у = —б = 1. Характерно, что главная часть этого выражения (формулы) содержит гамильтониан

=i[w2u2 — 3wu — 4- «z2w2 + 9 + —], (9)

0zL W2 4 4 2 J V/

ассоциированный с уравнением (P3) в случае а = в = 0,у = —б = 1. В работе [35] доказана

Теорема 2. Уравнение (Р3) представимо в виде системы Гамильтониана с гамильтонианом

^ _ apW2(u+P)2 ffoW(u+P) aw в__yzw2 5z

z z 2а0 2а0 4а0 4a0w2

где а0 ^ 0, р0 — произвольные постоянные; Р(г, ш), ш) — аналитические функции,

Формула (10) является обобщением (9), а также формулы гамильтониана Гарнье, ассоциированного с уравнением (Р3), и имеющего вид

1S 1 Го 2 2 о az I yz2w2 5z2T

1 z L 4 4w 8 8w2J

В работе [35] для пятого уравнения Пенлеве

— = г2(3ш — 1)ш’2 — — 1)ш’ + 2аш2(ш — 1)3 +

+2£(ш — 1)3 + — 1) + 2 Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

а = —/? = 1 (а2 + — с2), у = 0,5 = —2. Тогда функция д(5) = у(^)+1, 22 = ^ является

решением уравнения (20).

Теорема 4. Система (11) — (13) является системой Пенлеве-типа. Доказательство последнего утверждения основано на том, что общее решение уравнения (20) рациональным образом выражается через решение уравнения (Р5), которое не имеет подвижных критических особых точек. Остальные неизвестные функции р, и, V из системы (11) — (13) также не имеют подвижных критических особых точек, так как

— 1и = яд^д’У — (яд’)2 — ^д4 — ^

8^ = 4$д2 — 4и — и2 + ст,р = 5д’ — ^-ди.

2. Рассмотрим систему М. И18ака^ дифференциально-разностных уравнений

где £ — непрерывная независимая переменная, п — произвольный параметр. Система (21), (22) ассоциируется с уравнением (п + 1)5» = ¿(5п+т + 5п-1)(1 — 5»), представляющим второе дискретное уравнение Пенлеве и дискретным модифицированным уравнением Кортевега-де

Фриза = —(5»+т — 5»-т)(1 — 5»). Получена редукция системы (21), (22) к частному случаю

системы Пенлеве-типа [22], ассоциированной с уравнением (Р5) в случае 5 = 0.

3. Относительно переопределенной системы нелинейных уравнений в частных производных

где an — неизвестная функция независимых переменных х, у; n, р, q, — произвольные постоянные параметры;

Теорема 5. Система (23) совместна, если ху = z, а функция an = an(z) выражается через решения уравнения (Р5) с параметрами а = 2р, 2^ = —(п + 1)2,у = 2,5 = 2q, причем

Система (23) в случае р = q = 0 получена М. Hisakado при исследовании двумерного уравнения Тоды и струнных уравнений.

4. Рассмотрена система дифференциальных уравнений

q’ = р — qu + as, v’ = —pq — asq, (24)

p’ = sq — 2qv + pu + asu, u’ = — q2, (25)

где s — независимая переменная, a — произвольный постоянный параметр. В случае a = 0 система (24), (25) соответствует модели случайно-матричного типа с ядром Эйри. Характерной

особенностью системы (24), (25) является то, что она является системой Гамильтона с

гамильтонианом Н = ——— + q2v — pqu + asp — asqu и имеет первый интеграл

u2 — 2v — q2 = С, где С — произвольная постоянная. Имеет место

Теорема 6. Система (24), (25) является системой Пенлеве-типа. Ее решения выражаются через решения второго уравнения Пенлеве q» = 2q3 + (s + C)q + a’

5. Рассмотрена система нелинейных дифференциальных уравнений (отвечающая модели случайно-матричного типа с ядром Эрмита)

q’ = —sq + (V2N — 2u)p, w’ = p2, (26)

p’ = sp — (V2N + 2w)q, u’ = —q2, (27)

с неизвестными функциями q, w, p, u независимой переменной s и натуральным параметром N.

Теорема 7. Система дифференциальных уравнений (26), (27) удовлетворяет формальному тесту Пенлеве.

При этом получено представление решения системы (26), (27) в виде формальных рядов

q = a-1x-1 + a1x + a2x2 + ••• ,т = s — s0, w = (4a-1x)-1 + Ь0 + Ь1х + b2x2 + ••• p = (2a-1x)-1 + c1x + c2x2 +— u = a-1x-1 + u0 + u1x + u2x2 + •••,

содержащих четыре произвольных параметра s0, a-1 ^ 0, c1, c2.

6. Dyson процессы, описываемые системой нелинейных дифференциальных уравнений

r’ = —pu, u» = (x2 — 2n — 1)u + 2u2p, p» = (x2 — 2n + 1) + 2p2u , (28)

также ассоциируются с моделями случайно-матричного типа. В системе (28) р, г, и неизвестные функции независимой переменной х; п — произвольный постоянный параметр. Справедлива Теорема 8. Пусть w = w(x) решение уравнения

ш»’ — 6ш2ш’ + 2(х2 — 2п — 2)ш’ — 2ш2 + 4шх + 2х2 — 2(2п + 2) = 0. (29)

при фиксированном значении параметра п. Тогда функции и = ехр[/ ш(х^х], р = [и» — (х2 — 2п — 1)и](2и2)-1, г = т[—ш» + 2ш3 — 2ш(х2 — 2п — 1) — 2ст] (ст -произвольная постоянная) являются решениями системы (28).

Следует отметить, что последовательным преобразованием х ^ ¿х, ш ^ — ¿ш, ш = д(х) + х, ¿2 = —1 уравнение (29) сводится к уравнению третьего порядка относительно неизвестной функции д, первым интегралом которого является уравнение (Р4) с произвольным параметром в и 2а = п + 1.

Автомодельные редукции систем нелинейных уравнений в частных производных к

Как отмечалось во введении, одно из важнейших свойств уравнений Р—типа состоит в том, что они являются точными автомодельными редукциями хорошо известных нелинейных уравнений в частных производных и их высших аналогов. Указанное обстоятельство позволяет не только строить точные решения уравнений в частных производных, но и переносить некоторые хорошо известные свойства решений последних на решения уравнений Пенлеве-типа. 1. Система нелинейных уравнений в частных производных

Ф г — 3(ф^ + иф) = 0, (30)

с неизвестными функциями и, ф, ф независимых переменных х, £, (моделирующая процессы взаимодействия и распространения волн в плазме) введением новой независимой переменной = х + допускает редукцию к системе обыкновенных дифференциальных уравнений

ф’ — 3ф» — 3иф = 0, (31)

В системе (31) (‘) и (») обозначают производные первого и второго порядка соответственно по переменной г. Решения и(г), ф(г), ф(г), г = х + £ будем называть решениями типа бегущей волны системы (30). Наличие двух первых интегралов и + 6фф = сг, фф + 3(ф’ф — фф’) = с2 (с2,с2 — произвольные постоянные), а также первое уравнение системы (31) позволяют получить дифференциальное уравнение, которому удовлетворяет функция ф

(3с! — 18с2)ф2 + (1 + 18 с1)фф» + 9ф’2 + 27ф’ф» — 9фф»’ = 0. (32)

С помощью подстановки р(г) = ф’ф 1 уравнение (32) допускает понижение порядка

„„» ^2 1 + 18 С, СХ-6С2 „

р — 2р3 — р2——р——= 0. (33)

Решение уравнения (33) может быть представлено в терминах эллиптических функций Якоби.

2. В работах, связанных с исследованием моделей случайно-матричного типа, получено нелинейное уравнение в частных производных

где •Д» = £2=1х;2 —,п = 1,3; /- неизвестная функция независимых переменных

хг,х2, ^,х2Г. С уравнением (34) ассоциируется множество Е = и[=1[х2(-1,х2(] с М. Преобразованием = /(т), т = х1 + х2 + — х2г уравнение (34) сводится к уравнению

гш'»1 — 2тш’1 + + 6гш’2 = 0 = = «з^1), имеющему первый интеграл

ш»2 + 4ш’3 — ^тш’2 + ^^^ = сг, (35)

где — произвольная постоянная. Замена = А^, т = щ z, А]^ = 1, ц3 = г позволяет свести (35) к уравнению (5).

Теорема 9. Пусть w = — решение уравнения (5) при фиксированных значениях параметров а и 8. Тогда функция /(т) = А^^ш (— ),т = х1,х2, . х2Г, А^ = 1, ц3 = г является

решением уравнения (34).

3. Исследованы некоторые аналитические свойства автомодельных решений системы трех нелинейных уравнений в частных производных [36]

— а2и** — иуу — ид — аи2у = 0, (36)

у + а2^** + ууу + уд + аиу2 = 0, (37)

Чх* — а2дуу + = 0 (38)

с неизвестными функциями и, у, д независимых переменных х, у, £. В системе (36)-(38) а4 = 1, а — отличный от нуля параметр. Введением новой неизвестной функции ф = ехр(Я — ¿5), где Я = 11п(—иу),5 = 11п (— ¿2 = —1, система (36) — (38) сводится к резонансной системе Дэви-Стюартсона

¿ф + + фуу — 2ст2(|ф^| + ст2|фуу|)фЖ-1 — Чф + «Ж2ф = 0, (39)

9** — ^2Чуу — 2а(Ж2)^ = 0. (40)

Система (39), (40) является расширением хорошо известного резонансного уравнения Шредингера

Ж + — 2а2|ф**| • ф • |ф|-1 — а|ф|2ф = 0. (41)

Действительно, если неизвестные функции в системе (39)-(40) не зависят от у, то она вырождается в уравнение (41). При этом система (36)-(38) принимает вид

и£ — а2и** + аи2у = 0, (42)

и при редукционном ограничении у = и* (* — означает сопряжение к и), а также заменой £ ^ И она превращается в нелинейное уравнение Шредингера

— а2и** — а|и|2и = 0. (44)

Известно, что система (36)-(38) при выполнении определенного условия удовлетворяет тесту Вайса-Табора-Карневейла. Для случая, если система (36)-(38) не проходит тест Вайса-Табора- Карневейла, получены два семейства точных автомодельных решений, выражающихся через элементарные функции. Получена также редукция системы (36)-(38) к системе двух нелинейных связанных уравнений Шредингера с двумя независимыми переменными. На основании этого доказано существование у исследуемой системы автомодельных решений, порождаемых решениями уравнения (Р2), а также уравнения (Р4).

Говоря о приложениях уравнений Пенлеве-типа к моделям случайно-матричного типа, следует отметить, что важную роль здесь играют асимптотические свойства решений уравнений для полиномиальных гамильтонианов, ассоциированных с неприводимыми уравнениями Пенлеве. Важнейшей характеристикой системы в статистической физике, квантовой механики (где теория случайных матриц играет ведущую роль), как известно, является ее гамильтониан. Тест Пенлеве удобно применять к исследованию и других систем (подобных (26), (27)), ассоциированных с моделями случайно-матричного типа. При этом актуальным является доказательство сходимости формальных рядов Лорана, определяющих решение конкретной системы, если она проходит тест Пенлеве.

NONLINEAR DIFFERENTIAL EQUATIONS AND SYSTEMS WITH SPECIAL

PROPERTIES OF SOLUTIONS

V.V. TSEGELNIK Abstract

The results concerning the construction and research of analytic properties of solutions to nonlinear (ordinary and partial) differential equations and systems of special type are presented.

1. ГромакВ.И., ЦегельникВ.В. // Теорет. и матем. физика. 1983. Т. 55. №2. С. 189-196.

2. Цегельник В.В. // Теорет. и матем. физика. 1984. Т. 61. № 1. С. 155-160.

3. Цегельник В.В. // Докл. АН БССР. 1985. Т. 29. № 6. С. 497-500.

4. Громак В.И., Цегельник В.В. // Весщ АН БССР. Сер. ф1з.-мат. навук. 1988. № 1. С. 41-49.

5. Цегельник В.В. // Докл. АН БССР. 1988. Т. 32. № 5. С. 393-394.

6. Громак В.И., Цегельник В.В. // Теорет. и матем. физика. 1989. Т. 78. № 1. С. 22-34.

7. Громак В.И., Цегельник В.В. // Дифференц. уравнения. 1991. Т. 27. № 3. С. 396-402.

8. Громак В.И., Цегельник В.В. // Дифференц. уравнения. 1991. Т. 27. № 8. С. 1303-1312.

9. Цегельник В.В. // Весщ АН БССР. Сер. ф1з.-мат. навук. 1991. № 1. С. 118-120.

10. Цегельник В.В. // Дифференц. уравнения. 1994. Т.30. № 6. С. 992-997.

11. Громак В.И., Цегельник В.В. // Дифференц. уравнения. 1994. Т. 30. № 7. С. 1118-1124.

12. Цегельник В.В. // Теорет. и матем. физика. 1995. Т. 102. № 3. С. 364-366.

13. Фуксштейнер Б., Цегельник В.В. // Теорет. и матем. физика. 1995. Т. 105. № 2. С. 208-213.

14. Громак В.И., Цегельник В.В. // Дифференц. уравнения. 1996. Т. 32. № 8. С. 1018-1023.

15. Цегельник В.В. // Дифференц. уравнения. 1996. Т. 32. № 10. С. 1434-1435.

16. Цегельник В.В. // Теорет. и матем. физика. 1997. Т. 113. № 2. С. 285-288.

17. Цегельник В.В. // ДАН БССР. 1997. Т 41. № 3. С. 17-20.

18. Цегельник В.В. // Докл. АН БССР. Сер. ф1з.-мат. навук. 1997. № 3. С. 132-133.

19. Цегельник В.В. // Изв. ВУЗов. Прикл. нелинейная динамика. 1998. Т. 6. № 5. С. 84-88.

20. Цегельник В.В. // Весщ НАН Беларуси Сер. ф1з.-мат. навук. 1998. № 3. С. 61-63.

21. Tsegelnik V. V. //Reqular and chaotic dynamics. 1999. Vol. 4. № 4. P. 77-80.

22. Цегельник В.В. // Дифференц. уравнения. 1999. Т. 35. №7. С. 1003-1004.

23. Цегельник В.В. // Дифференц. уравнения. 2000. Т. 36. № 3. С. 425-426.

24. Цегельник В.В. // Докл. НАН Беларуси. 2000. Т. 44. № 3. С. 12-13.

25. Цегельник В.В. // Труды Ин-та математики НАН Беларуси. 2000. Т. 6. С. 139-141.

26. Цегельник В.В. // Докл. НАН Беларуси. 2001. Т. 45. № 2. С. 50-53.

27. Цегельник В.В. // Труды Ин-та математики НАН Беларуси. 2004. Т. 12. № 2. С. 176-179.

28. Цегельник В.В. // Докл. БГУИР. 2004. № 1. С. 64-72.

29. Цегельник В.В. // Докл. БГУИР. 2006. № 2. С. 142-148.

30. Цегельник В.В. // Докл. НАН Беларуси. 2006. Т. 50. № 5. С. 22-24.

31. Цегельник В.В. // Теорет. и матем. физика. 2007. Т. 151. № 1. С. 54-65.

32. Цегельник В.В. // Докл. БГУИР. 2008. № 2. С. 137-139.

33. Цегельник В.В. // Некоторые аналитические свойства и приложения решений уравнений Пенлеве-типа Минск 2007.

34. Цегельник В.В. // Докл. НАН Беларуси. 2010. Т. 54. № 1. С. 21-25.

35. Цегельник В.В. // Теорет. и матем. физика. 2010. Т. 162. № 1. С. 69-71.

36. Цегельник В.В. // Вестн. нац. исслед. ядерного университета «МИФИ». 2013. Т. 2. № 4. С. 422-424.

СВЕДЕНИЯ ОБ АВТОРE

Цегельник Владимир Владимирович родился (1954 г.р.). Окончил механико-математический факультет БГУ им. В.И. Ленина в 1977 г., в 1984 г. -заочную аспирантуру этого же университета по специальности дифференциальные уравнения и математическая физика. В 1985 г. защитил кандидатскую диссертацию, в 2002 г. — докторскую. С 1999 г. занимает должность заведующего кафедрой высшей математики БГУИР. Автор более 150 научных и научно-методических публикаций, среди которых ряд учебных пособий, монография и более 40 научных статей. Научные интересы — аналитическая теория нелинейных дифференциальных уравнений Пенлеве-типа и их приложения.

Общая характеристика нелинейных систем

1. Определение нелинейной системы

К нелинейным системам относятся все системы, которые не могут быть описаны линейными дифференциальными уравнениями. Нелинейные системы очень многообразны, поэтому практически нельзя говорить о едином “классе” нелинейных систем, противостоящем классу линейных систем. Исследование нелинейных систем связано с преодолением значительных математических трудностей. Основная трудность состоит в том, что не существует единого точного метода решения нелинейных уравнений и для каждого вида нелинейности приходится изыскивать специфический частный метод.

Для описания системы автоматического управления могут быть всегда выбраны такие n координат состояния объекта , при которых уравнения, описывающие процессы в системе, принимают вид

, (22.1)

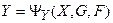
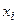
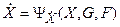
где вектор состояния X с координатами задается системой дифференциальных уравнений первого порядка в матричной форме

(22.2)

Здесь вектор Y выражает m управляемых переменных, вектор G выражает l задающих воздействий, а вектор F – соответственно k внешних воздействий.

Если рассматривать систему при детерминированных воздействиях, то есть внешние воздействия G и F являются известными функциями времени t, то в этом случае уравнения (22.1) и (22.2) примут вид:

, (22.3)

. (22.4)

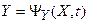
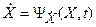
Уравнение (22.4) – это матричная запись n нелинейных дифференциальных уравнений первого порядка рассматриваемой системы порядка n:

. (22.5)

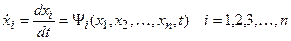
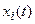
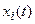
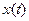
В матричном описании САУ весьма существенен рациональный выбор координат состояния, описывающих систему. Обычно руководствуются соображениями простоты уравнения (22.3), выражающего управляемую величину через координаты состояния и стремлением не иметь разрывов в функциях . Решение системы уравнений (22.5) при заданных начальных условиях дает возможность для каждой координаты состояния определить описывающую ее функцию времени , а процесс, наблюдаемый в системе, изобразить в виде линии в n – мерном пространстве координат состояния, для которого время t является параметром точки кривой, соответствующей уравнению .

Изображение процесса в пространстве состояний дает возможность наглядно проследить изменение всех координат состояния на любом интервале t от 0 до ¥.

Уравнения (22.5) охватывают широкий класс систем, хотя, конечно, и не исчерпывают всего их многообразия. Существенный интерес представляет класс систем, когда система уравнения состоит из ряда линейных элементов и связей, объединенных в одну линейную часть (ЛЧ) и одного нелинейного элемента. В этом случае дифференциальные уравнения системы могут быть записаны следующим образом:

(22.6)

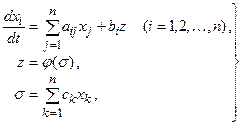
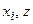
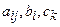
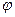
где — координаты;

— постоянные вещественные коэффициенты;

— нелинейная функция.

Система (22.6) интересна тем, что целый ряд практических систем управления одной величины может быть сведен к данной схеме. В дальнейшем ограничимся рассмотрением в основном нелинейных систем, уравнения которых могут быть приведены к виду (22.5) и к виду (22.6). Для этих систем характерно то, что исходная система уравнений может быть разрешена относительно первых производных всех координат по времени и, таким образом, приведена к виду, где под знаком нелинейной функции стоят только сами переменные, но не их производные.

Математический аппарат анализа нелинейных систем связан с необходимостью исследования нелинейных дифференциальных уравнений, теория которых содержит множество индивидуальных методов, присущих различным видам уравнений, описывающих систему. Сложность решения нелинейных дифференциальных уравнений вызывает необходимость создания ряда приближенных методов, позволяющих судить о характере процессов, наблюдаемых в системе. При этом нелинейные характеристики реальных элементов системы заменяют некоторыми идеализированными приближенными характеристиками, которые обусловлены как характером нелинейного элемента, так и принятым методом анализа системы.

Методы анализа и синтеза нелинейных САУ весьма разнообразны и выбор того или иного метода зависит от постановки задачи исследования, вида нелинейности и порядка дифференциального уравнения, описывающего систему.

Для решения нелинейных уравнений, кроме аналитических и графических методов, широко применяют методы моделирования с помощью аналоговой вычислительной техники (АВМ) и численного решения задач с помощью цифровых вычислительных машин (ЦВМ).

Простота моделирования нелинейных звеньев, наглядность получаемых решений фиксируемых обычно на осциллографе или самопишущих приборах, легкость изменения различных параметров моделируемой системы – все это обеспечило массовое применение АВМ для анализа и синтеза нелинейных систем управления.

Несмотря на большие трудности исследования нелинейных систем, интерес к ним за последнее время резко возрос. Это объясняется в частности, тем, что по показателям качества процесса регулирования (быстродействие, точность) нелинейные системы очень часто превосходят соответствующие линейные системы. Это относится к таким системам, в которые целенаправленно вводятся специальные нелинейности, определяющие эффективность динамических процессов.

Выдающаяся роль в создании и развитии методов исследования нелинейных систем принадлежит русским ученым. Наиболее важный вклад в эту область бал сделан А.М.Ляпуновым, опубликовавшим в 1892 году свою работу “Общая задача об устойчивости движения”. В этой работе было впервые дано определение понятия устойчивости движения и разработаны методы решения этой задачи. До настоящего времени методы, предложенные А.М.Ляпуновым, являются наиболее строгими при исследовании динамики нелинейных систем.

В 1937 году были опубликованы фундаментальные работы А.А.Андронова и С.Э.Хайкина “Теория колебаний”, а также Н.М.Крылова и Н.Н.Боголюбова “Введение в нелинейную механику”. Эти работы, получившие мировую известность, послужили основой для решения важных исследований нелинейных систем.

2.Типовые нелинейные характеристики и особенности процессов в нелинейных САУ

Нелинейности, встречающиеся в системах автоматического управления, могут иметь различный характер. Некоторые нелинейности вводится специально для получения требуемых динамических характеристик регулирования или из-за экономических соображений, т.е. тогда, когда проектируемая с преднамеренно вводимой нелинейностью система имеет выигрыш в весе, стоимости, размерах. При этом предполагается, что рабочие характеристики такой системы должны удовлетворять заданным требованиям.

Другие звенья с нелинейными характеристиками, встречающиеся в системах автоматического управления, нежелательны, и их появление объясняется физическими свойствами отдельных элементов системы. Например, кулоновское трение, прилипание, люфт, насыщение определяют нелинейные участки характеристик звеньев, которые необходимо учитывать при исследовании соответствующих систем.

Нелинейные характеристики в зависимости от вида могут быть разделены на две группы: аналитические и неаналитические. Аналитические характеристики нелинейных звеньев имеют вид плавных однозначных кривых или семейства плавных кривых.

Эти характеристики, как правило, можно описать достаточно простым уравнением. Характеристики неаналитические обычно представляются прерывными или неоднозначными с резкими перегибами.

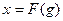
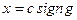
На рис. 22.1 показаны различные формы характеристики реле. Очевидно, такие характеристики невозможно линеаризовать. Идеальная характеристика реле без среднего положения (рис. 22.1,а) может быть представлена так:

,

где символ sign обозначает знак входного сигнала.

Релейные характеристики реле отличаются от рассмотренной выше. Релейная характеристика реле с зоной нечувствительности показана на рис. 22.1,б. Эта характеристика может быть описана следующим образом:

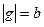
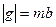
На рис. 22.1,в показана характеристика реле с зоной нечувствительности и петлей гистерезисного типа. Петля характеристики определяется тем, что входной сигнал срабатывания реле больше, чем сигнал отпускания , где m – коэффициент возврата. Аналитическая запись такой характеристики имеет вид:

Рис. 22.1. Релейные характеристики нелинейных элементов

Характеристика реле без среднего положения, имеющая только петлю гистерезисного типа, показана на рис. 22.1,г. Она может быть описана так:

Если реле работает в режиме включения входной цепи одной полярности, то соответствующая характеристика будет иметь несимметричный характер (рис. 22.1, д, е).

Выше рассмотрены были характеристики реле, которые имеют существенно нелинейный характер, однако характеристики и все другие релейных звеньев систем автоматического регулирования в той или иной мере отличаются от идеальной прямой линии. И только для ограниченного интервала изменения входного сигнала некоторые из этих характеристик приближенно можно считать линейными.

На рис. 22.2 показаны нелинейные характеристики некоторых других звеньев систем автоматического регулирования. Характеристика нелинейного элемента (рис. 22.2, а) может быть приближенно описана следующим образом:

где , .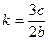

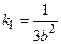
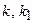
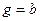
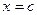
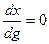
Коэффициенты найдены из условия при , и .

Как видно из рис. 22.2,а, эта характеристика имеет линейную зону и участки насыщения. Под зоной понимается участок характеристики, охватывающий начало координат.

Характеристика элемента с ограничением выходной координаты (рис. 22.2,б) может быть описана так:

Как и предыдущая, характеристика с ограничением выходной координаты имеет зону линейности и участки насыщения.

На рис. 22.2,в показана характеристика звена с зоной нечувствительности и линейными участками. Эта характеристика имеет следующую зависимость выходной координаты от входного сигнала:

Характеристика, изображенная на рис. 22.2,г, по сравнению с предыдущей имеет еще и участки насыщения. Поэтому уравнения для этой характеристики будут иметь вид:

На рис. 22.2,д показана нелинейная характеристика в виде гистерезисной петли. Такая характеристика, имеющая зону неоднозначности, становится особенно сложной, когда ее форма зависит от величины входного сигнала.

Нелинейная характеристика, учитывающая зазор соединений, изображена на рис. 22.2,е. Как и для предыдущего случая, определяющим участком этой характеристики является зона неоднозначности. Соответствующие уравнения имеют вид:

где .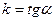

На рис. 22.2,ж показана характеристика нелинейного элемента, имеющего переменный коэффициент усиления.

Рис. 22.2. Характеристики нелинейных элементов

На примере рассмотренных характеристик нелинейных элементов (рис. 22.1, рис. 22.2) можно сделать вывод о том, что наиболее характерными участками этих характеристик являются зоны нечувствительности, зоны и участки линейности, зоны неоднозначности и участки насыщения.

Исследование нелинейных систем является весьма актуальной и важной задачей. Этому вопросу посвящено большое количество работ. Полученные результаты, однако, не являются универсальными и могут быть успешно использованы лишь для решения определенного класса задач.

3. Методы линеаризации нелинейных моделей

При проектировании нелинейных систем автоматического регулирования возникает необходимость в исследовании влияния нелинейных звеньев системы на динамические процессы при всевозможных режимах работы. Для такого рода исследований существует достаточно много различных методов, которые, однако, не могут рассматриваться как универсальные и успешно решают поставленную задачу лишь для определенного типа нелинейности.

Наиболее широкое распространение получили следующие методы анализа нелинейных систем:

— линейной аппроксимации (линеаризации);

Метод линейной аппроксимации. Этот метод применим для анализа таких нелинейных систем, характеристики которых могут быть представлены аналитическими функциями. В этом случае нелинейные функции могут быть разложены в ряд Тейлора. Примерами нелинейных характеристик такого типа являются кривые намагничивания из ферромагнитных материалов. В этом случае, когда нелинейная характеристика имеет резкие перегибы и разрывы, она не может быть описана аналитической функцией. Поэтому исследование таких нелинейностей, как люфт, трение и др., с помощью линейной аппроксимации не представляется возможным.

Если характер нелинейности известен и допускает линеаризацию, приступают к аппроксимации нелинейной характеристики в окрестности предполагаемой рабочей точки. При этом, обычно, используется два способа: метод касательных (разложение в ряд Тейлора) и метод наименьших квадратов. Метод касательных учитывает только первый член ряда Тейлора, поэтому он очень прост и легко может быть применен к характеристикам, заданным как аналитически, так и графически. Метод наименьших квадратов дает лучшую аппроксимацию по критерию минимума среднеквадратической ошибки. Этот метод целесообразно применять в том случае, если рабочая область нелинейной характеристики достаточно велика.

Основное преимущество линейной аппроксимации заключается в том, что в дальнейшем используется линейная методика исследования, что особенно важно при анализе сложных систем автоматического регулирования. Полученные результаты будут справедливы лишь в том случае, если величина входного воздействия нелинейного элемента не выходит за допустимые пределы, поэтому теоретические расчеты должны проверяться экспериментом.

Метод кусочно-линейной аппроксимации. Этот метод предназначен для случая больших вариаций возмущающих воздействий. При этом нелинейные характеристики могут иметь изломы и скачки. Вся характеристика разбивается на прямолинейные участки. Для каждого из этих участков составляются линейные дифференциальные уравнения. Решение этих уравнений производится для определенного диапазона изменения возмущающих сигналов и начальных условий. Рассматриваемый способ может дать очень точные результаты, но для этого потребуется выполнить большой объем вычислительной работы. Объем работы особенно возрастает при исследовании систем высокого порядка и в случае, когда нелинейная характеристика при аппроксимации разбивается на большое число отрезков.

Численные методы. Численные методы интегрирования позволяют решать нелинейные дифференциальные уравнения высокого порядка при больших вариациях возмущающих воздействий относительно рабочей точки. Основной недостаток этих методов заключается в том, что каждый полученный результат характеризует только данную конкретную задачу и не может быть использован при исследовании других нелинейных систем. Каждый из численных методов имеет свои особенности, поэтому задача исследователя заключается в выборе такого численного метода, который наиболее удобен при решении данной конкретной задачи.

Метод фазового пространства (фазовой плоскости). Этот метод является наиболее совершенным аппаратом исследования нелинейных систем, который позволяет получить полную картину возможного поведения системы для различных начальных условий и возмущающих воздействий в виде ступенчатого или линейно-возрастающего сигнала. Метод фазовой плоскости применим для исследования систем с нелинейными элементами с любыми характеристиками. Применяя графическое интегрирование, на основе этого метода можно получить динамические характеристики систем во временной области.

Основной недостаток этого метода заключается в том, что он полностью применим лишь для систем второго порядка. Применение этого метода даже для систем третьего порядка связано с очень большими вычислительными трудностями.

Метод гармонической линеаризации. Этот метод позволяет использовать обычный аппарат частотных характеристик, хорошо известный в линейном анализе. При этом нелинейному элементу приводится в соответствие линейный элемент с эквивалентным комплексным коэффициентом передачи (усиления), который можно рассматривать как своеобразный аналог передаточной функции. Эквивалентный комплексный коэффициент усиления может быть получен в предположении, что входной сигнал нелинейного элемента синусоидален, а выходная координата может быть представлена основной гармоникой ее разложения в ряд Фурье.

Метод гармонической линеаризации достаточно прост и особенно удобен для определения параметров автоколебаний в системе, причем точность этого метода возрастает с увеличением порядка системы. Это объясняется тем, что с увеличением порядка системы возрастают ее фильтрующие свойства, то есть способность подавлять высокочастотные составляющие сигнала. Недостатками этого метода являются малая точность при анализе простых систем, ограничение количества исследуемых нелинейностей и весьма приближенная оценка переходного процесса.

Моделирование. Использование моделирующей установки позволяет исследовать сложные системы со многими нелинейностями при широких вариациях как начальных условий, так и возмущающих воздействий. Такой подход является обязательным на заключительном этапе проектирования, когда объективная оценка системы становится особенно важной. Моделирование нашло применение и при выявлении влияния разброса отдельных параметров на динамические характеристики процесса регулирования.

Дата добавления: 2015-12-11 ; просмотров: 4392 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ