Системы уравнений, как математические модели реальных ситуаций
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Системы уравнений как математические модели реальных ситуаций
Вам известно, что система двух уравнений с двумя переменными может служить математической моделью реальной ситуации. Первый опыт в решении таких задач вы приобрели в курсе алгебры 7-го класса. Правда, там встречались только системы двух линейных уравнений с двумя переменными. В § 4 мы рассмотрели задачу, математическая модель которой представляла собой систему двух уравнений, но одно из них уже не было линейным. Вернитесь еще раз к этой задаче, и вы убедитесь, что в технологии ее решения ничего особенно нового не было — те же три этапа математического моделирования. То же относится и к задачам, которые рассматриваются в этом параграфе.
В райцентре два кинотеатра — «Факел» и «Слава», первый — на 400, а второй — на 600 мест. В зрительном зале кинотеатра «Слава» на 4 ряда больше, чем в кинотеатре «Факел», и, кроме того, в каждом ряду на 5 мест больше, чем в кинотеатре «Факел». Сколько рядов в зрительном зале кинотеатра «Факел», если известно, что в каждом ряду кинотеатра «Слава» более 25 мест?
Первый этап.
Составление математической модели.
Пусть х — число рядов в кинотеатре «Факел», у — число мест в каждом ряду кинотеатра «Факел». Тогда х + 4 — число рядов в кинотеатре «Слава», у + 5 — число мест в каждом ряду кинотеатра «Слава». Зная число рядов и число мест в ряду, можно найти общее число мест в каждом кинотеатре: ху — число мест в кинотеатре «Факел», (х + 4)(у +5) — число мест в кинотеатре «Слава». По условию, в кинотеатре «Факел» — 400 мест, т.е. ху — 400, а в кинотеатре «Слава» — 600 мест, т.е. (х + 4)<у + 5) = 600.
Таким образом, мы приходим к системе двух уравнений с двумя переменными:
Математическая модель задачи составлена.
Работа с составленной моделью. Имеем
Применим метод алгебраического сложения: вычтем первое уравнение из второго. Получим
Заменим этим уравнением второе уравнение системы (1):
Система (2) несколько проще, чем система (1), ее можно решить методом подстановки. Выразим у через х из второго уравнения системы
Подставим это выражение вместо у в первое уравнение системы (2):
(обе части предыдущего уравнения почленно разделили на 5); 
Так как 
то получаем: если х = 20, то у = 20; если x = 16, то у = 25.
Итак, система (2), а с ней и система (1) имеют два решения: (20; 20) и (16; 25).
Ответ на вопрос задачи.
Опираясь на полученные решения системы, мы должны проанализировать две возможности: либо в кинотеатре «Факел» 20 рядов по 20 мест в каждом ряду, либо 16 рядов по 25 мест в каждом ряду. Если выбрать первую возможность, то в кинотеатре «Слава» будет 24 ряда (по условию, там на 4 ряда больше) по 25 мест в каждом ряду (по условию, в каждом ряду «Славы» на 5 мест больше, чем в «Факеле»). Это нас не устраивает, поскольку, по условию, в каждом ряду «Славы» более 25 мест. Рассмотрим вторую возможность: в «Факеле» 16 рядов по 25 мест в каждом. Тогда в «Славе» будет 20 рядов по 30 мест в каждом. Это нас устраивает.
Ответ: 16 рядов.
На самом деле эта задача не является для вас новой, мы решали ее в учебнике «Алгебра-8», но по-другому: математической моделью задачи было рациональное уравнение с одной переменной. Приведем краткие наброски для составления такой модели:
Получаем уравнение 
Это математическая модель задачи.
Сравним два варианта решения задачи. В первом варианте была более сложная математическая модель (система уравнений), значит, более трудным был второй этап — работа с составленной моделью. Зато менее трудным был первый этап, сама математическая модель была составлена легче и быстрее. Поскольку первый этап, где больше творчества, сложнее, чем второй (технический), то часто предпочтительнее упрощать именно этап составления модели, т.е. работать с двумя переменными .
Пристани В и С находятся ниже пристани А по течению реки соответственно на 30 км и 45 км (рис. 41). Моторная лодка отходит от пристани А, доходит до С, сразу поворачивает назад и приходит в В, затратив на весь путь 4 ч 40 мин. В другой раз эта же лодка отошла от пристани С, дошла до А, сразу повернула назад и пришла в В, затратив на весь путь 7 ч. Чему равны собственная скорость лодки и скорость течения реки?
Составление математической модели. Введем две переменные: х км/ч — собственная скорость лодки, у км/ч — скорость течения реки. Тогда х + у км/ч — скорость движения лодки по течению реки, х-у км/ч — скорость движения лодки против течения реки. Рассмотрим первый рейс лодки. Он составил 45 км по течению и 15 км против течения. Имеем: 
— время движения лодки от А до С (в первом рейсе), 
время движения лодки от С до В (в первом рейсе). Всего на первый рейс лодка затратила 4 ч 40 мин, т.е. 
Таким образом, получаем уравнение 
Рассмотрим второй рейс лодки. Он составил 45 км против течения и 30 км по течению. Имеем: 
время движения лодки от С до А (во втором рейсе), 
время движения лодки от А до В (во втором рейсе). Всего на второй рейс лодка затратила 7 ч. Таким образом, получаем уравнение 
Математическая модель задачи представляет собой систему двух уравнений с двумя переменными: 
Второй этап.
Работа с составленной моделью. Для решения системы уравнений воспользуемся методом введения новых переменных. Положим: 
Тогда система примет вид 
Решив эту систему двух линейных уравнений с двумя переменными а и Ь (сделайте это!), получим 
Итак,
Остается решить совсем простую систему уравнений
Получаем х = 12, у = 3.
Третий этап. Ответ на вопрос задачи.
Требуется определить скорость лодки в стоячей воде и скорость течения реки. Первую скорость мы обозначили буквой х, получили х = 12; значит, собственная скорость лодки составляет 12 км/ч. Скорость течения мы обозначили буквой у, получили у = 3. Значит, скорость течения реки составляет 3 км/ч.
Ответ: 12 км/ч; 3 км/ч.
Мастер и его ученик планировали сообща выполнить некоторую работу за 6 дней. Сначала за дело взялся ученик. Выполнив 20% задания, он заболел. Остальная работа пришлась на долю мастера. В итоге выполнение задания растянулось на 11 дней. За сколько дней мог бы его выполнить мастер и за сколько дней ученик, действуя в одиночку, если известно, что и то и другое количество дней выражаются целыми числами?
Составление математической модели.
Если речь идет о выполнении некоторой работы, не охарактеризованной в количественном плане (т.е. не сказано, сколько деталей надо сделать, сколько кубометров земли вынуть и т.д.), то объем работы считают равным 1, а части работы выражают в долях единицы. Пусть х — число дней, необходимых мастеру, чтобы выполнить в одиночку всю работу, а у — число дней, необходимых ученику, чтобы справиться в одиночку со всей работой. Если объем всей работы (т.е. 1) разделить на число дней, то узнаем долю работы, выполняемую за 1 день.
Итак, 
— доля работы, которую выполняет мастер за 1 день, 
доля работы, которую выполняет ученик за 1 день.
По условию, работая вместе, мастер и ученик могли бы выполнить всю работу за 6 дней. Доля работы мастера за 6 дней выражается формулой — 
Доля работы ученика за 6 дней выражается формулой 
Поскольку вместе они выполнят всю работу (т.е. 1), составляем уравнение 
По условию, ученик выполнил, трудясь в одиночку до своей болезни, 20% задания, т.е. 
часть всей работы. Сколько времени он потратил? Естественно, что часть того времени, которое нужно ему на выполнение всей работы, т.е. 
дней. Потом пришел мастер, сделал оставшуюся работу, т.е. 
задания, на что затратил 
дней. По условию, выполнение задания растянулось на 11 дней, т.е. 
Таким образом, математическая модель задачи составлена — система двух уравнений с двумя переменными 
Работа с составленной моделью. Воспользуемся методом подстановки. Выразим у через х из второго уравнения системы: у = 55-4x. Подставим выражение 55-4x вместо у в первое уравнение системы: 
Решая это рациональное уравнение, последовательно получаем:
Оба найденных значения удовлетворяют условию 
т.е. являются корнями рационального уравнения с переменной х. Осталось найти соответствующие значения у. Для этого воспользуемся уравнением y = 55 — 4x. Если х = 10, то из этого уравнения находим у = 15; если 
то из того же уравнения находим у = 22. Итак, составленная система уравнений имеет два решения:
Ответ на вопрос задачи.
По условию, количество дней, необходимых как мастеру, так и ученику для выполнения в одиночку всего задания, выражается целым числом. Значит, пара 
нас не устраивает. Остается лишь одна возможность: х = 10, у = 15.
О т в е т: 10 дней; 15 дней.
Обратите внимание на то, что, решая системы уравнений, составленные в рассмотренных задачах, мы применили все методы, о которых шла речь в предыдущем параграфе: и подстановки, и алгебраического сложения, и введения новых переменных.
Системы уравнений как математические модели реальных ситуаций
Разделы: Математика
Классы: 8 , 9
Ключевые слова: Текстовые задачи , вызывают затруднения
Цели:
- Обобщить решение задач с помощью систем уравнений различными методами.
- Воспитывать интерес к предмету через межпредметные связи с химией и литературой, обращая внимание на аккуратность, дисциплинированность и самостоятельность.
- Развивать устную и письменную речь, внимание и логическое мышление.
Оборудование:
- компьютер и проектор;
- тексты задач для решения в классе;
- тексты задач для решения дома;
Тип урока: урок обобщения и систематизации знаний.
Подготовка к уроку: повторение способов решения задач с помощью систем уравнений различными методами.
Комментарий к уроку: использование презентации Microsoft Power Point.
Эпиграф к уроку: Учитель должен много знать, и не только свой предмет, он должен быть компетентным в разных областях. …
План урока:
- Организационный момент (сообщение о необходимости решения задач с помощью систем уравнений, связь темы урока с КИМами ГИА по математике).
- Актуализация опорных знаний (повторение методов решения систем уравнений).
- Закрепление материала (решение задач путем математического моделирования).
- Итоги урока. Домашнее задание.
Слайд 1: Системы уравнений как математические модели реальных ситуаций.
Слайд 2: “Все науки настолько связаны между собою, что легче изучать их все сразу, нежели какую-либо одну из них в отдельности от всех прочих”. Рене Декарт
Слайд 3: Методы решения систем уравнений:
– подстановки;
– алгебраического сложения;
– введения новых переменных;
– графический.
Слайд 4: Алгоритм решения задачи с помощью системы уравнений:
1. Обозначить неизвестные элементы переменными;
2. Составить по условию задачи систему уравнений;
3. Определить метод решения системы уравнений;
4. Выбрать ответ, удовлетворяющий условию задачи.
Слайд 5: Этапы решения задачи:
Первый этап.
Составление математической модели.
Второй этап.
Работа с составленной моделью.
Третий этап.
Ответ на вопрос задачи.
Слайд 6: Л.Н. Толстой “Арифметика”
У двух мужиков 35 овец. У одного на 9 овец больше, чем у другого. Сколько у каждого овец?
I этап. Обозначим х – число овец у первого мужика, у – у второго.
II этап. (Решаем методом алгебраического сложения.)
IIIэтап. Ответ: 13 и 22.
Слайд 7: Илья Ильф и Евгений Петров “Двенадцать стульев”
Слайд 8: Задача: Потом отец Федор подошел к комоду и вынул из конфетной коробки 50 рублей трехрублевками и пятирублевками. В коробке оставалось еще 20 рублей.
Сколько трех- и пятирублевок отец Федор взял и сколько оставил?
Ну, а чтобы обеспечить единственность решения, добавим условие: отец Федор взял с собой большую часть трехрублевок и большую часть пятирублевок. Теперь найдите решение.
а) Пусть взято x трехрублевок и y пятирублевок
3x+5y=50 находим пары: 5 и 7, 10 и 4, 15 и 1
б) а – осталось трехрублевок
b – осталось пятирублевок
3а+5b=20 находим пары: 5 и 1, 0 и 4
Значит, отец Федор взял 5 трехрублевок и 7 пятирублевок или 10 трехрублевок и 4 пятирублевок.
Слайд 10: Задачи от Н.Носова из книги “Витя Малеев школе и дома”
Задача 1.
Мальчик и девочка рвали в лесу орехи. Они сорвали всего 120 штук. Девочка сорвала в два раза меньше мальчика. Сколько орехов собрал каждый из них?I этап. Пусть мальчик сорвал х ор., а девочка у ор.
II этап. (Решаем методом подстановки.)
III этап. Ответ: мальчик сорвал 80 ор., а девочка сорвала 40 ор.
Задача 2.
В магазине было 8 пил, а топоров в три раза больше. Одной бригаде плотников продали половину топоров и три пилы за 84 рубля. Оставшиеся топоры и пилы продали другой бригаде плотников за 100 рублей. Сколько стоит один топор и одна пила?I этап. Пусть топор стоит х руб., а пила стоит у руб.
II этап. (Решаем методом алгебраического сложения.)
III этап. Ответ: топор стоит 5 руб. и пила стоит 8 руб.
Слайд 13: Задача из рассказа А.П. Чехова “Репетитор”
Купец купил 138 аршин черного и синего сукна за 540 руб. Спрашивается, сколько аршин купил он того и другого сукна, если синее стоило 5 руб. за аршин, а черное – 3 руб?
Слайд 14: Решение:
Пусть черного сукна приобрел купец – х м и синего сукна – у м. Так как синее сукно стоит 5 руб. за 1м, а черное – 3 руб. за 1м, то составим и решим систему уравнений:
II этап. (метод подстановки)
x = 138 – y
5(138 – y) + 3y = 540
5(138 – y) + 3y = 540
690 – 5y +3y = 540
-2y = -150
y = 75 x = 138 – 75 = 63.III этап. Ответ: 63 (аршина) – синего и 75 (аршин) – черного сукна приобрел купец.
Имеются два сплава меди со свинцом. Один сплав содержит 15% меди, а другой 65%. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?
I этап: Пусть первого сплава взяли х г и второго – у г.
Имеется руда из двух пластов с содержанием меди 6% и 11%. Сколько “бедной” руды надо взять, чтобы получить при смешивании с “богатой” 20 т руды с содержанием меди 8%?
Переведем проценты в дроби: 6%=0,06; 11%=0,11; 8%=0,08
I этап:
Пусть надо взять х т “бедной” руды, которая будет содержать 0,06х т меди, а “богатой” руды надо взять у т, которая будет содержать 0,11у т меди. Составим первое уравнение: х + у = 20.Так как получившиеся 20 т руды будут содержать 20*0,08=1,6 т меди, то получим уравнение:
II этап: (метод подстановки)
Решив систему уравнений, получим х = 12.
III этап: Ответ: 12 т руды с 6% содержанием меди
Имеются сплавы золота и серебра. В одном эти металлы находятся в отношении 2: 3, а в другом в отношении 3: 7. Сколько нужно взять от каждого сплава, чтобы получить 1 кг нового, в котором золото и серебро находились бы в отношении 5: 11?
I этап: По этой схеме уравнение х + у =1 показывает массу нового сплава.
Определяем массу золота в каждом сплаве и получаем уравнение
* х +
Аналогично массу серебра и получаем уравнение
II этап: Записываем одну из систем:
х + у = 1
х + у = 1
Решая ее, получаем х = 0,125 и у = 0,875
III этап: Ответ: 125 г золота и 875 г серебра.
Слайд 18: Задания из тестов ГИА:
1. Найти пары чисел, являющиеся решением системы уравнений
1) (1; 6); (6; 1) 2) (6; 1); (?0, 5; ?12)
Слайд 19:
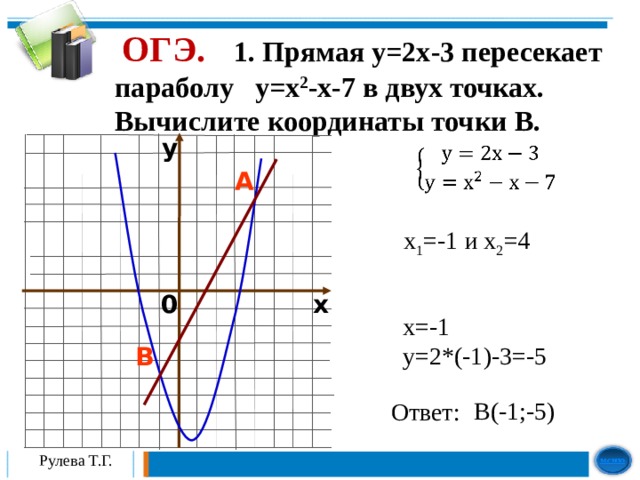
2. Прямая y=2x-3 пересекает параболу y=x2-x-7 в двух точках.
Вычислите координаты точки B.Слайд 20:
3. Вычислите координаты точки B.
Слайд 21:
Домашнее заданиеЗадачник под ред. Мордковича А.Г. №7.37, 7.40 и 7.53)
Спасибо всем за урок! Удачи! И помните: “Учение без размышления бесполезно, но и размышление без учения опасно”. (Конфуций.)
Системы уравнений как математические модели реальных ситуаций
Текстовые задачи, решаемые с помощью систем уравнений, включены в различные сборники заданий по математике ГИА. У учеников они вызывают затруднения, потому что таким задачам в школьном курсе уделяется мало внимания. Существуют различные способы решения задач, в том числе с помощью систем уравнений с двумя неизвестными. Важно показать, что такие задачи можно встретить даже в художественной литературе.
Просмотр содержимого документа
«Системы уравнений как математические модели реальных ситуаций»
МОУ «Средняя школа №43»
Системы уравнений как математические модели реальных ситуаций
Математике должно учить в школе еще с той целью, чтобы познания, здесь приобретаемые, были достаточными для обыкновенных потребностей в жизни. Л. Карно
Этапы решения задачи
Алгоритм решения задачи с помощью систем уравнений
Решение задач с помощью систем уравнений
Задания из тестов ОГЭ
1.Сумма двух чисел равна 15. Одно больше другого в 2
раза. Найти эти числа.
2.Разность двух чисел равна 8. Одно больше другого в 3
раза. Найти эти числа.
3.В классе 23 ученика. Мальчиков на 5 больше, чем девочек. Сколько девочек и сколько мальчиков в классе?
4.Скорость теплохода по течению 24 км/ч, а против течения 20 км/ч. Определите собственную скорость теплохода и скорость течения реки.
Задача на движение
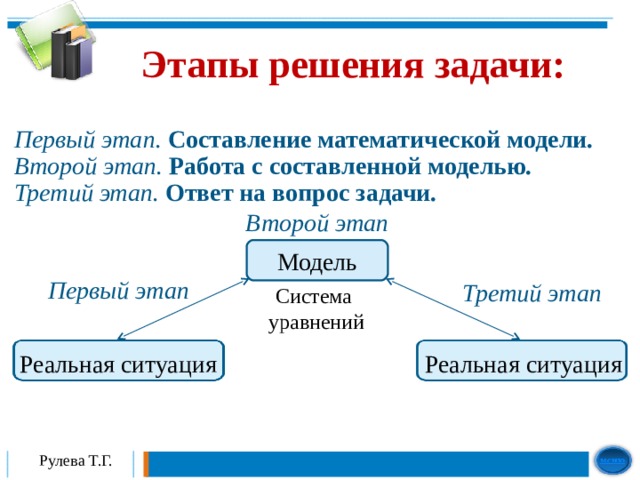
Из двух городов, расстояние между которыми 650 км, выехали навстречу друг другу два поезда, через 10 часов они встретились. Если же первый поезд отправится на 4ч 20мин раньше, то встреча произойдёт через 8 часов после отправления второго поезда. Сколько километров в час проходит каждый поезд?
Этапы решения задачи:
Первый этап. Составление математической модели. Второй этап. Работа с составленной моделью. Третий этап. Ответ на вопрос задачи.
Алгоритм решения задачи с помощью системы уравнений:
1. Обозначить неизвестные элементы переменными.
2. Составить по условию задачи систему уравнений.
3. Определить метод решения системы уравнений.
4. Выбрать ответ, удовлетворяющий условию задачи.
1 этап: «Составление математической модели».
2 этап: «Работа с составленной моделью».
Ответ: скорость поездов — 3 0км/ч и 35 км/ч .
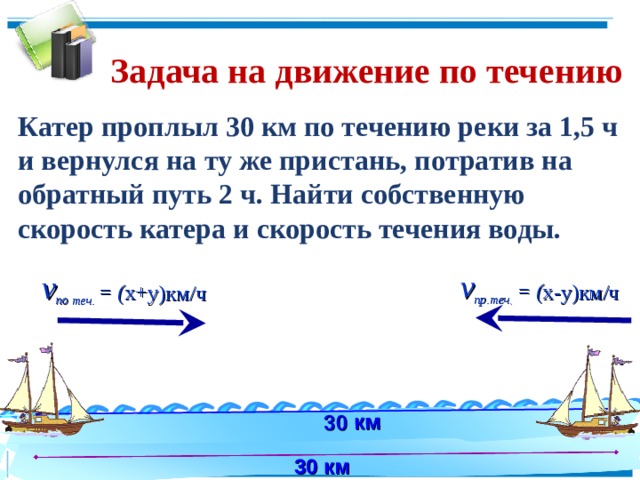
Задача на движение по течению
Катер проплыл 30 км по течению реки за 1,5 ч и вернулся на ту же пристань, потратив на обратный путь 2 ч. Найти собственную скорость катера и скорость течения воды.
1 этап: «Составление математической модели».
х – собст. скорость
у – скорость течения
2 этап: «Работа с составленной моделью».
3 этап. Ответ: собственная скорость катера – 17,5км/ч и скорость течения реки – 2,5 км/ч.
Бассейн наполняется двумя трубами при совместной работе за 1 час. Наполнение бассейна только через первую трубу длится вдвое дольше, чем через вторую трубу. За какой промежуток времени каждая труба отдельно может наполнить бассейн?
1 этап: «Составление математической модели».
2 этап: «Работа с составленной моделью».
3 этап. Ответ: вторая труба заполняет бассейн за 1,5 ч, а первая труба за 3ч .
Гимнастика для глаз!
ОГЭ. 1. Прямая y=2x-3 пересекает параболу y=x 2 -x-7 в двух точках. Вычислите координаты точки B .
источники:http://urok.1sept.ru/articles/600344
http://multiurok.ru/files/sistemy-uravnenii-kak-matematicheskie-modeli-realn.html
* х + 
* у = 
* 1
* х + 
* у = 
* 1
х + 
у =
х + 
у =
у 650 8 I II 2 этап: «Работа с составленной моделью». I II 3 этап. Ответ: скорость поездов — 3 0км/ч и 35 км/ч . Рулева Т.Г. » width=»640″
