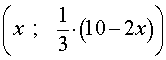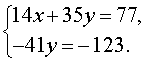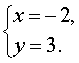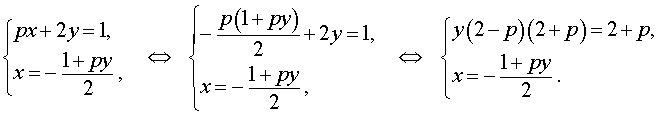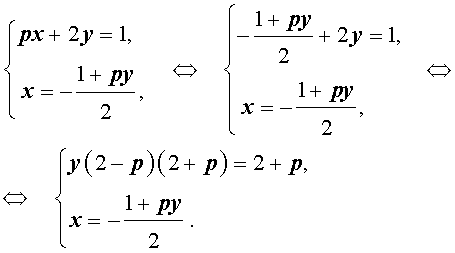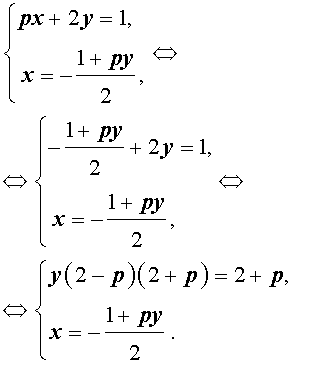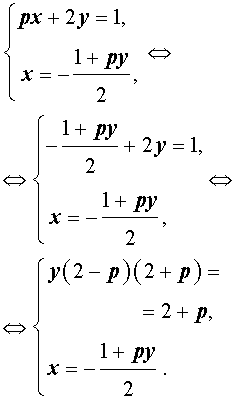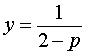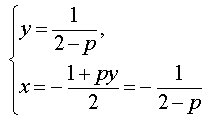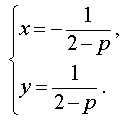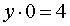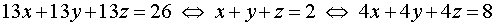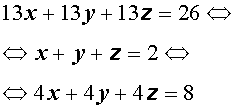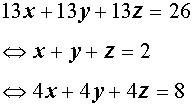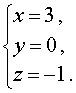Системы уравнений первой степени 9 класс

Системы линейных уравнений

Линейные уравнения (уравнения первой степени) с двумя неизвестными

Системы из двух линейных уравнений с двумя неизвестными

Системы из трех линейных уравнений с тремя неизвестными

Линейные уравнения (уравнения первой степени) с двумя неизвестными

Определение 1 . Линейным уравнением (уравнением первой степени) с двумя неизвестными x и y называют уравнение, имеющее вид

где a , b , c – заданные числа.

Определение 2 . Решением уравнения (1) называют пару чисел (x ; y) , для которых формула (1) является верным равенством.

Пример 1 . Найти решение уравнения

Решение . Выразим из равенства (2) переменную y через переменную x :

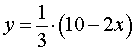(3)

Из формулы (3) следует, что решениями уравнения (2) служат все пары чисел вида

где x – любое число.

Замечание . Как видно из решения примера 1, уравнение (2) имеет бесконечно много решений. Однако важно отметить, что не любая пара чисел (x ; y) является решением этого уравнения. Для того, чтобы получить какое-нибудь решение уравнения (2), число x можно взять любым, а число y после этого вычислить по формуле (3).

Системы из двух линейных уравнений с двумя неизвестными

Определение 3 . Системой из двух линейных уравнений с двумя неизвестными x и y называют систему уравнений, имеющую вид

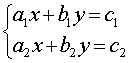(4)

Определение 4 . В системе уравнений (4) числа a₁ , b₁ , a₂ , b₂ называют коэффициентами при неизвестных , а числа c₁ , c₂ – свободными членами .

Определение 5 . Решением системы уравнений (4) называют пару чисел (x ; y) , являющуюся решением как одного, так и другого уравнения системы (4).

Определение 6 . Две системы уравнений называют равносильными (эквивалентными) , если все решения первой системы уравнений являются решениями второй системы, и все решения второй системы являются решениями первой системы.

Равносильность систем уравнений обозначают, используя символ «»

Системы линейных уравнений решают с помощью метода последовательного исключения неизвестных , который мы проиллюстрируем на примерах.

Пример 2 . Решить систему уравнений

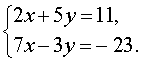(5)

Решение . Для того, чтобы решить систему (5) исключим из второго уравнения системы неизвестное х .

С этой целью сначала преобразуем систему (5) к виду, в котором коэффициенты при неизвестном x в первом и втором уравнениях системы станут одинаковыми.

Если первое уравнение системы (5) умножить на коэффициент, стоящий при x во втором уравнении (число 7 ), а второе уравнение умножить на коэффициент, стоящий при x в первом уравнении (число 2 ), то система (5) примет вид

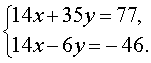(6)

Теперь совершим над системой (6) следующие преобразования:

• первое уравнение системы оставим без изменений;
• из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.

В результате система (6) преобразуется в равносильную ей систему

Из второго уравнения находим y = 3 , и, подставив это значение в первое уравнение, получаем

Пример 3 . Найти все значения параметра p , при которых система уравнений

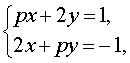(7)

а) имеет единственное решение;

б) имеет бесконечно много решений;

в) не имеет решений.

Решение . Выражая x через y из второго уравнения системы (7) и подставляя полученное выражение вместо x в первое уравнение системы (7), получим

Следовательно, система (7) равносильна системе

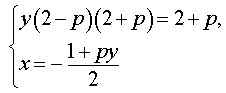(8)

Исследуем решения системы (8) в зависимости от значений параметра p . Для этого сначала рассмотрим первое уравнение системы (8):

Если , то уравнение (9) имеет единственное решение

Следовательно, система (8) равносильна системе

Таким образом, в случае, когда , система (7) имеет единственное решение

Если p = – 2 , то уравнение (9) принимает вид

,

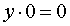
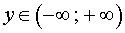
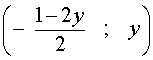
и его решением является любое число . Поэтому решением системы (7) служит бесконечное множество всех пар чисел

,

где y – любое число.

Если p = 2 , то уравнение (9) принимает вид

и решений не имеет, откуда вытекает, что и система (7) решений не имеет.

Системы из трех линейных уравнений с тремя неизвестными

Определение 7 . Системой из трех линейных уравнений с тремя неизвестными x , y и z называют систему уравнений, имеющую вид

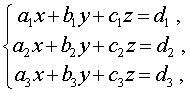(10)

Определение 9 . Решением системы уравнений (10) называют тройку чисел (x ; y ; z) , при подстановке которых в каждое из трех уравнений системы (10) получается верное равенство.

Пример 4 . Решить систему уравнений

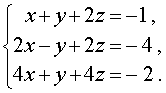(11)

Решение . Будем решать систему (11) при помощи метода последовательного исключения неизвестных .

Для этого сначала исключим из второго и третьего уравнений системы неизвестное y , совершив над системой (11) следующие преобразования:

• первое уравнение системы оставим без изменений;
• ко второму уравнению прибавим первое уравнение и заменим второе уравнение системы на полученную сумму;
• из третьего уравнения вычтем первое уравнение и заменим третье уравнение системы на полученную разность.

В результате система (11) преобразуется в равносильную ей систему

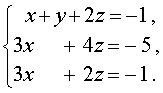(12)

Теперь исключим из третьего уравнения системы неизвестное x , совершив над системой (12) следующие преобразования:

• первое и второе уравнения системы оставим без изменений;
• из третьего уравнения вычтем второе уравнение и заменим третье уравнение системы на полученную разность.

В результате система (12) преобразуется в равносильную ей систему

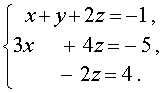(13)

Из системы (13) последовательно находим

Пример 5 . Решить систему уравнений

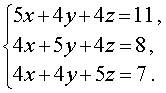(14)

Решение . Заметим, что из данной системы можно получить удобное следствие, сложив все три уравнения системы:

Если числа (x ; y ; z) являются решением системы (14), то они должны удовлетворять и уравнению (15). Однако в таком случае числа (x ; y ; z) должны также быть решением системы, которая получается, если из каждого уравнения системы (14) вычесть уравнение (15):

Поскольку мы использовали следствие из системы (14), не задумываясь о том, являются ли сделанные преобразования системы (14) равносильными, то полученный результат нужно проверить. Подставив тройку чисел (3 ; 0 ; –1) в исходную систему (14), убеждаемся, что числа (3 ; 0 ; –1) действительно являются ее решением.

Замечание . Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы с нелинейными уравнениями» и нашим учебным пособием «Системы уравнений».

Системы уравнений первой степени

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

МБОУ «Средняя общеобразовательная школа №14»

Урок «Системы уравнений первой степени»

(с использованием элементов игровых технологий)

Составила учитель высшей категории:

Гусева Тамара Михайловна.

Тема урока: « Системы уравнений первой степени»

Цель урока: 1 ) закрепление и углубление знаний по теме «Решение систем уравнений»

2)развитие логического мышления.

I . Организационный момент. Домашнее задание:

II. Повторение изученного.

Чтобы узнать тему урока, класс решает анаграмму.

и записывает тему урока.

При решении систем уравнений важно правильно выполнять вычисления, решать уравнения.

Вычислить: а) 2 ∙ — 1 = б) 3-3 ∙ = в) 2 — 1,2 ∙ 5 =

Решить уравнения: а) 2x = ; б) y = 6; в) = — 4.

Выразить X через Y и Y через Х:

Вопросы классу: а) что называется решением системы уравнений?

Проверить, какая пара чисел является решением системы уравнений.

а) (-2; 3) (3; -2)

б) (2; 2) (0,5; 1,5)

Вопросы классу: а) что значит решить систему уравнений?

б) какими способами мы решаем системы

в) в чем заключается каждый способ?

Разобрать способы решения домашних систем.

+ = 5,

+ =1;

III . Закрепление изученного.

Иногда можно с помощью системы уравнений записать ту или иную ситуацию.

а) Сумма двух чисел равна 17. Одно из чисел на 17 меньше другого.

б) Периметр прямоугольного участка 400 м. длина его в 3 раза больше ширины.

Я просила вас дома придумать задачи, которые можно описать следующими системами:

а)

Обратить внимание на тексты, т.к. решение системы (15,5; 10,5)

б)

Прочесть свою задачу: по тропинке вдоль кустов

сосчитать я также смог,

что шагало 30 ног.

Это вместе шли куда-то

петухи и поросята.

А теперь вопрос таков:

сколько было петухов?

И узнать я был бы рад,

Сколько было поросят?

А теперь решим систему тремя способами (по рядам):

(три человека решают за отворотами)

А сейчас познакомимся еще с одним способом решения этой же системы – по формулам Крамера.

(Группа сильных ребят заранее приготовила презентацию, в которой знакомит одноклассников со способом решения систем по формулам Крамера)

IV . В конце урока «Поле чудес». Классу раздаются карточки с системами. На доске «сетка» с

ответами. Ребята решают систему, выбирают ответ, записывают на листочке фамилию, номер

карточки, ответ и выбранную букву, и сдают ответ учителю. Учитель записывает под номером

соответствующую букву и в конце концов класс прочитает фразу:

«МАТЕМАТИКА УМ В ПОРЯДОК ПРИВОДИТ»

№1. (2; -1) М

№2. (1; -1) А

№3. (4; 3) Т

№4. (7,8; 0,8) Е

№5. (2; -1) М

№6. (1; -1) А

№7. (4;3) Т

№8. (2; 1) И

№9. (0,5; 1,5) К

№10. (1; -1) А

№11. ( — ; 2) У

№12. (2; -1) М

№13. (3; 3) В

№14. (1; 2) П

№15. (5; -1) О

№16. (-3,5; -3) Р

№17. (5,75; 6,5) Я

№18. (4; -3) Д

№19. (5; -1) О

№20. (0,5; 1,5) К

№21. (1; 2) П

№22. (-3,5; -3) Р

№23. (2; 1) И

№24. (3; 3) В

№25. (5; -1) О

№26. (4; -3) Д

№27. (2; 1) И

№28. (4; 3) Т

«Сетка» с ответами

( — ; 2)

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 949 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 681 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 314 человек из 70 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 567 169 материалов в базе

Другие материалы

• 14.12.2015
• 730
• 1

• 14.12.2015
• 1153
• 0

• 14.12.2015
• 713
• 0

• 14.12.2015
• 6150
• 10

• 14.12.2015
• 13799
• 216

• 14.12.2015
• 1555
• 7

• 14.12.2015
• 4059
• 15

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 14.12.2015 848
• DOCX 147 кбайт
• 5 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Гусева Тамара Михайловна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет и 2 месяца
• Подписчики: 0
• Всего просмотров: 909
• Всего материалов: 1

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Онлайн-конференция о создании школьных служб примирения

Время чтения: 3 минуты

Объявлен конкурс дизайн-проектов для школьных пространств

Время чтения: 2 минуты

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

В Воронеже продлили удаленное обучение для учеников 5-11-х классов

Время чтения: 1 минута

Рособрнадзор не планирует переносить досрочный период ЕГЭ

Время чтения: 0 минут

Количество бюджетных мест в вузах по IT-программам вырастет до 160 тыс.

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Уравнения и системы уравнений первой степени

Уравнения и системы уравнений первой степени

Два числа или какие-нибудь выражения, соединенные знаком « = », образуют равенство. Если данные числа или выражения при любых значениях букв равны, то такое равенство называют тождеством.

Например, когда утверждают, что при любом а действительном:

а + 1 = 1 + а, здесь равенство является тождеством.

Уравнением называется равенство, содержащее неизвестные числа, обозначенные буквами. Эти буквы называют неизвестными. Неизвестных в уравнении может быть несколько.

Например, в уравнении 2х + у = 7х – 3 два неизвестных: х и у.

Выражение, стоящее в уравнении слева (2х + у) называют левой частью уравнения, а выражение, стоящее в уравнении справа (7х – 3), называют правой его частью.

Значение неизвестного, при котором уравнение становится тождеством, называется решением или корнем уравнения.

Например, если в уравнение 3х + 7=13 вместо неизвестного х подставить число 2, получим тождество . Следовательно, значение х = 2 удовлетворяет данному уравнению и число 2 есть решение или корень данного уравнения.

Два уравнения называются равносильными (или эквивалентными), если все решения первого уравнения являются решениями второго и наоборот, все решения второго уравнения являются решениями первого. К равносильным уравнениям относятся также уравнения, не имеющие решений.

Например, уравнения 2х – 5 = 11 и 7х + 6 = 62 равносильны, так как они имеют один и тот же корень х = 8; уравнения х + 2 = х + 5 и 2х + 7 = 2х равносильны, потому что оба не имеют решений.

Свойства равносильных уравнений

1. К обеим частям уравнения можно прибавить любое выражение, имеющее смысл при всех допустимых значениях неизвестного; полученное уравнение будет равносильно данному.

Пример. Уравнение 2х – 1 = 7 имеет корень х = 4. Прибавив к обеим частям по 5, получим уравнение 2х – 1 + 5 = 7 + 5 или 2х + 4 = 12, которое имеет тот же корень х = 4.

2. Если в обеих частях уравнения имеются одинаковые члены, то их можно опустить.

Пример. Уравнение 9х + 5х = 18 + 5х имеет один корень х = 2. Опустив в обеих частях 5х, получим уравнение 9х = 18, которое имеет тот же корень х = 2.

3. Любой член уравнения можно перенести из одной части уравнения в другую, изменив его знак на противоположный.

Пример. Уравнение 7х — 11 = 3 имеет один корень х = 2. Если перенести 11 в правую часть с противоположным знаком, получим уравнение 7х = 3 + 11, которое имеет то же решение х = 2.

4. Обе части уравнения можно умножить на любое выражение (число), имеющее смысл и отличное от нуля при всех допустимых значениях неизвестного, полученное уравнение будет равносильно данному.

Пример. Уравнение 2х — 15 = 10 – 3х имеет корень х = 5. Умножив обе части на 3, получим уравнение 3(2х – 15) = 3(10 – 3х) или 6х – 45 =30 – 9х, которое имеет тот же корень х = 5.

5. Знаки всех членов уравнения можно изменить на противоположные (это равносильно умножению обеих частей на (-1)).

Пример. Уравнение – 3х + 7 = – 8 после умножения обеих частей на (-1) примет вид 3х — 7 = 8. Первое и второе уравнения имеют единственный корень х = 5.

6. Обе части уравнения можно разделить на одно и тоже число, отличное от нуля (то есть, не равное нулю).

Пример. Уравнение имеет два корня: и . Разделив все его члены на 3, получим уравнение , равносильное данному, так как оно имеет те же два корня: и .

7. Уравнение, в котором коэффициенты всех или нескольких членов дробные числа, можно заменить равносильным ему уравнением с целыми коэффициентами, для этого обе части уравнения надо умножить на наименьшее общее кратное знаменателей дробных коэффициентов.

Пример. Уравнение после умножения обеих частей на 14 примет вид:

. Легко убедиться в том, что первое и последнее уравнения имеют корень х = 10.

Уравнения первой степени

Уравнение с одним неизвестным, которое после раскрытия скобок и приведения подобных членов принимает вид , где произвольные числа, х – неизвестное, называется уравнением первой степени с одним неизвестным (или линейным уравнением с одним неизвестным).

Пример. 2х + 3 = 7 – 0,5х ; 0,3х = 0.

Уравнение первой степени с одним неизвестным всегда имеет одно решение; линейное уравнение может не иметь решений () или иметь их бесконечное множество ().

Пример. Решить уравнение .

Решение. Умножим все члены уравнения на наименьшее общее кратное знаменателей, равное 12.

.

После сокращения получим: . Раскроем скобки, чтобы отделить члены, содержащие неизвестное и свободные члены:

.

Сгруппируем в одной части (левой) члены, содержащие неизвестное, а в другой части (правой) — свободные члены:

. Приведем подобные члены: . Разделив обе части на (-22), получим х = 7.

Системы двух уравнений первой степени с двумя неизвестными

Уравнение вида , где называется уравнением первой степени с двумя неизвестными х и у. Если находят общие решения двух и более уравнений то говорят, что эти уравнения образуют систему, их записывают обычно одно под другим и объединяют фигурной скобкой, например .

Каждая пара значений неизвестных, которая одновременно удовлетворяет обоим уравнениям системы, называется решением системы. Решить систему – это значит найти все решения этой системы или показать, что она их не имеет. Две системы уравнений называются равносильными (эквивалентными), если все решения одной из них являются решениями другой и наоборот, все решения другой являются решениями первой.

Например, решением системы является пара чисел х = 4 и у = 3. Эти числа являются также единственным решением системы . Следовательно, эти системы уравнений равносильны.

Способы решения систем уравнений

1. Способ алгебраического сложения. Если коэффициенты при каком-нибудь неизвестном в обоих уравнениях равны по абсолютной величине, то складывая оба уравнения (или вычитая одно из другого), можно получить уравнение с одним неизвестным. Решая это уравнение, определяют одно неизвестное, а подставляя его в одно из уравнений системы, находят второе неизвестное.

Примеры: Решить системы уравнений: 1) .

Здесь коэффициенты при у по абсолютной величине равны между собой, но противоположны по знаку. Для получения уравнения с одним неизвестным уравнения системы почленно складываем:

Полученное значение х = 4 подставляем в какое-нибудь уравнение системы, например в первое, и находим значение у: .

2) .

Уравняем коэффициенты при х. Для этого умножим первое уравнение на 3, а второе на (– 2) и сложим полученные уравнения.

Ответ: .

2. Способ подстановки. Из любого уравнения системы одну из неизестных выражаем через остальные, а затем подставляем значение этой неизвестной в остальные уравнения. Рассмотрим этот способ на конкретных примерах:

1) Решим систему уравнений . Выразим из первого уравнения одно из неизвестных, например х: и подставим полученное значение х во второе уравнение системы, получим уравнение с одним неизвестным у:

Подставим у = 1 в выражение для х, получим .

Ответ: .

2) . В этом случае удобно выразить у из второго уравнения:

. Полученное значение у подставляем в первое уравнение и получаем уравнение с одним неизвестным х:

Подставим значение х = 5 в выражение для у, получим .

Ответ: .

3) Решим систему уравнений . Из первого уравнения находим . Подставив это значение во второе уравнение, получим уравнение с одним неизвестным у:

Подставим у = 5 в выражение для х, получим

Ответ: .

3. Способ замены. К cистемам двух линейных уравнений с двумя неизвестными можно приводить некоторые нелинейные системы. Это можно осуществлять способом замены.

Пример. Решить систему. .

Перепишем систему в виде: . Заменим неизвестные, положив , получим линейную систему . Из первого уравнения выразим неизвестное . Подставим значение во второе уравнение, получим уравнение с одним неизвестным:

. Подставив значение v в выражение для t, получим: . Из соотношений находим .

Ответ: .

Исследование системы уравнений

Исследуем сколько решений может иметь система уравнений , где — коэффициенты при неизвестных, — свободные члены.

А) Если , то система имеет единственное решение.

Б) Если , то система не имеет решений.

В) Если , то система имеет бесконечное множество решений.

Пример. . В данной системе отношение коэффициентов при одинаковых неизвестных не равны (), значит система имеет единственное решение.

Действительно, .

.

Ответ: .

Пример. . В данной системе или после сокращения , следовательно, система не имеет решений.

Пример. . В данной системе или после сокращения , значит, система имеет бесконечное множество решений.

Уравнения, содержащие модуль

При решении уравнений, содержащих модуль, используется понятие модуля действительного числа. Модулем (абсолютной величиной) действительного числа а называется само это число, если и противоположное число ( – а), если . Модуль числа а обозначается .

Итак, . Например, , так как число 3 > 0; , так как число – 5 0, то квадратное уравнение имеет два решения (корня): и .

Если D = 0, квадратное уравнение, очевидно, имеет два одинаковых решения (кратных корня).