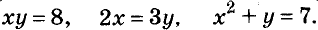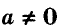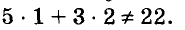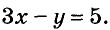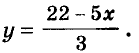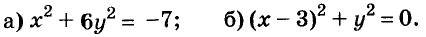Алгебра. 7 класс
Решение задач при помощи систем уравнений первой степени
Решение задач при помощи систем уравнений
Решение задач при помощи систем уравнений
Составление краткой записи к задаче
Решение системы уравнений
Составление системы уравнений по условию задачи
Необходимо запомнить
Решая задачу алгебраическим способом, вы можете составить как уравнение, так и систему уравнений. И в том, и другом случае, необходимо пройти 3 этапа:
- Разбор условия задачи и составление уравнения или системы уравнений. На данном этапе может быть выполнена краткая запись или рисунок к задаче.
- Решение составленного уравнения или системы уравнений.
- Использование полученного решения для ответа на вопрос задачи.
Системы уравнений первой степени с тремя неизвестными
Решим задачу алгебраическим способом.
Задача: Даны $3$ числа, сумма которых равна $23$. Если к удвоенному первому числу прибавить второе число и вычесть третье, то получится $32$. А если из первого числа вычесть удвоенное второе и прибавить третье, то получится $8$.
В задаче $3$ неизвестных, поэтому введем следующие обозначения:
Пусть $х$ – первое число, у – второе число, $z$ – ё третье число.
Мысленно разделим условие задачи на $3$ части, по каждой из которых составим уравнение с тремя неизвестными:
Сумма трех чисел равна $23$, значит $х + у + z = 23$.
Удвоенное первое число равно $2х$. Получаем уравнение: $2х + у – z = 32$.
Удвоенное второе число равно $2у$. Составляем уравнение: $х – 2у + z = 8$.
Объединяем три уравнения в систему:
Мы получили систему трёх уравнений первой степени с тремя неизвестными. Покажем, как можно решить эту систему уравнений способом подстановки. Из третьего уравнения системы выражаем $х$ через $y$ и $z$ : $х = 8 + 2у – z$. И подставляем $8 + 2у-z$ вместо $х$ в первое и второе уравнение. Получаем систему уравнений с двумя неизвестными:
Приведем подобные члены:
Таким образом, мы свели систему уравнений с тремя неизвестными к системе уравнений с двумя неизвестными.
Решая систему, находим, что $у_0 = 5$, $z_0 = 3$.
Подставим $у_0$ и $z_0$ в $х = 8 + 2у-z$, находим, что $х_0 = 15$.
Таким образом, мы решили систему трёх уравнений с тремя неизвестными.
Вернемся к условию задачи: первое число $15$, второе число $5$, третье число $3$.
Системы линейных уравнений с примерами решений
Содержание:
Системы уравнений, как и отдельные уравнения, используют для решения сложных и необходимых задач. Системы уравнений бывают с двумя, тремя и более переменными. В этой главе вы ознакомитесь с простейшими системами двух уравнений с двумя переменными. Основные темы лекции:
- уравнения с двумя переменными;
- график линейного уравнения;
- системы уравнений;
- способ подстановки;
- способ сложения;
- решение задач составлением системы уравнений.
Уравнения с двумя переменными
До сих пор мы рассматривали уравнение с одной переменной. Однако существуют задачи, решение которых приводит к уравнениям с двумя переменными.
Пример:
На 22 руб. купили несколько книжек по 5 руб. и географических карт — по 3 руб. Сколько купили книжек и карт?
Решение:
Пусть купили х книжки у карт. За книжки заплатили 5х руб., а за карты — 3у руб. Всего заплатили 22 руб., то есть, 5х + Зу = 22.
Это уравнение с двумя переменными. Приведём и другие примеры таких уравнений с двумя переменными:
Уравнение вида ах + by = с, где а, b, с — данные числа, называется линейным уравнением с двумя переменными х и у. Если
Примеры линейных уравнений:
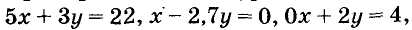
Паре чисел х = -1 и у = 9 удовлетворяет уравнение 5х + Зу -= 22, так как 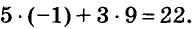
Каждая пара чисел, удовлетворяющая уравнение с двумя переменными, т. е. обращающая это уравнение в верное равенство, называется решением этого уравнения.
Обратите внимание: одно решение состоит из двух чисел, на первом месте записывают значение х, на втором — у. Корнями их не называют.
Чтобы найти решение уравнения с двумя переменными, следует подставить в уравнение произвольное значение первой неременной и, решив полученное уравнение, найти соответствующее значение второй переменной.
Для примера найдем несколько решений уравнения
Если х = 1, то 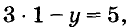
Уравнение 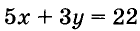
Два уравнения с двумя переменными называют равносильными, если каждое из них имеет те же решения, что и другое. Уравнения, не имеющие решений, также считаются равносильными.
Для уравнения с двумя переменными остаются справедливыми свойства, сформулированные для уравнений с одной переменной.
Обе части уравнения с двумя переменными можно умножить или разделить на одно и то же число, отличное от нуля. Любой член такого уравнения можно перенести из одной части уравнения в другую, изменив его знак на противоположный. В результате получается уравнение, равносильное данному.
Например, уравнение 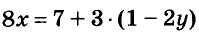
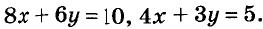
Иногда возникает потребность решить уравнение с двумя переменными во множестве целых чисел, то есть определить решения, являющиеся парами целых чисел. Способы решения таких уравнений определил древнегреческий математик Диофант (III в.), поэтому их называют диофантовыми уравнениями. Например, задача о книжках и картах сводится к уравнению 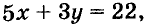
Переменную у из этого уравнения выразим через х:
Будем подставлять в равенство вместо х первые натуральные числа до тех пор, пока не получим целое значение переменной у. Это можно делать устно. Если х = 2, то у = 4. Других натуральных решений уравнение не имеет. Поэтому задача имеет единственное решение: 2 книги и 4 карты.
Пример:
Решение:
а) При любых значениях х и у значения выражения 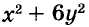
б) Значение выражения 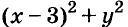
Пример:
Составьте уравнение с двумя переменными, решением которого будет пара чисел (1; -5).
Решение:
Пишем любой двучлен с переменными х и у, например 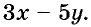
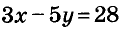
Есть много других линейных уравнений с двумя переменными, имеющих такое же решение (1; -5).
График линейного уравнения с двумя переменными
Рассмотрим уравнение 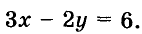
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Уравнения и системы уравнений первой степени
Уравнения и системы уравнений первой степени
Два числа или какие-нибудь выражения, соединенные знаком « = », образуют равенство. Если данные числа или выражения при любых значениях букв равны, то такое равенство называют тождеством.
Например, когда утверждают, что при любом а действительном:
а + 1 = 1 + а, здесь равенство является тождеством.
Уравнением называется равенство, содержащее неизвестные числа, обозначенные буквами. Эти буквы называют неизвестными. Неизвестных в уравнении может быть несколько.
Например, в уравнении 2х + у = 7х – 3 два неизвестных: х и у.
Выражение, стоящее в уравнении слева (2х + у) называют левой частью уравнения, а выражение, стоящее в уравнении справа (7х – 3), называют правой его частью.
Значение неизвестного, при котором уравнение становится тождеством, называется решением или корнем уравнения.
Например, если в уравнение 3х + 7=13 вместо неизвестного х подставить число 2, получим тождество 
Два уравнения называются равносильными (или эквивалентными), если все решения первого уравнения являются решениями второго и наоборот, все решения второго уравнения являются решениями первого. К равносильным уравнениям относятся также уравнения, не имеющие решений.
Например, уравнения 2х – 5 = 11 и 7х + 6 = 62 равносильны, так как они имеют один и тот же корень х = 8; уравнения х + 2 = х + 5 и 2х + 7 = 2х равносильны, потому что оба не имеют решений.
Свойства равносильных уравнений
1. К обеим частям уравнения можно прибавить любое выражение, имеющее смысл при всех допустимых значениях неизвестного; полученное уравнение будет равносильно данному.
Пример. Уравнение 2х – 1 = 7 имеет корень х = 4. Прибавив к обеим частям по 5, получим уравнение 2х – 1 + 5 = 7 + 5 или 2х + 4 = 12, которое имеет тот же корень х = 4.
2. Если в обеих частях уравнения имеются одинаковые члены, то их можно опустить.
Пример. Уравнение 9х + 5х = 18 + 5х имеет один корень х = 2. Опустив в обеих частях 5х, получим уравнение 9х = 18, которое имеет тот же корень х = 2.
3. Любой член уравнения можно перенести из одной части уравнения в другую, изменив его знак на противоположный.
Пример. Уравнение 7х — 11 = 3 имеет один корень х = 2. Если перенести 11 в правую часть с противоположным знаком, получим уравнение 7х = 3 + 11, которое имеет то же решение х = 2.
4. Обе части уравнения можно умножить на любое выражение (число), имеющее смысл и отличное от нуля при всех допустимых значениях неизвестного, полученное уравнение будет равносильно данному.
Пример. Уравнение 2х — 15 = 10 – 3х имеет корень х = 5. Умножив обе части на 3, получим уравнение 3(2х – 15) = 3(10 – 3х) или 6х – 45 =30 – 9х, которое имеет тот же корень х = 5.
5. Знаки всех членов уравнения можно изменить на противоположные (это равносильно умножению обеих частей на (-1)).
Пример. Уравнение – 3х + 7 = – 8 после умножения обеих частей на (-1) примет вид 3х — 7 = 8. Первое и второе уравнения имеют единственный корень х = 5.
6. Обе части уравнения можно разделить на одно и тоже число, отличное от нуля (то есть, не равное нулю).
Пример. Уравнение 





7. Уравнение, в котором коэффициенты всех или нескольких членов дробные числа, можно заменить равносильным ему уравнением с целыми коэффициентами, для этого обе части уравнения надо умножить на наименьшее общее кратное знаменателей дробных коэффициентов.
Пример. Уравнение 

Уравнения первой степени
Уравнение с одним неизвестным, которое после раскрытия скобок и приведения подобных членов принимает вид 

Пример. 2х + 3 = 7 – 0,5х ; 0,3х = 0.
Уравнение первой степени с одним неизвестным всегда имеет одно решение; линейное уравнение может не иметь решений (

Пример. Решить уравнение 
Решение. Умножим все члены уравнения на наименьшее общее кратное знаменателей, равное 12.

После сокращения получим: 

Сгруппируем в одной части (левой) члены, содержащие неизвестное, а в другой части (правой) — свободные члены:


Системы двух уравнений первой степени с двумя неизвестными
Уравнение вида 


Каждая пара значений неизвестных, которая одновременно удовлетворяет обоим уравнениям системы, называется решением системы. Решить систему – это значит найти все решения этой системы или показать, что она их не имеет. Две системы уравнений называются равносильными (эквивалентными), если все решения одной из них являются решениями другой и наоборот, все решения другой являются решениями первой.
Например, решением системы 

Способы решения систем уравнений
1. Способ алгебраического сложения. Если коэффициенты при каком-нибудь неизвестном в обоих уравнениях равны по абсолютной величине, то складывая оба уравнения (или вычитая одно из другого), можно получить уравнение с одним неизвестным. Решая это уравнение, определяют одно неизвестное, а подставляя его в одно из уравнений системы, находят второе неизвестное.
Примеры: Решить системы уравнений: 1) 
Здесь коэффициенты при у по абсолютной величине равны между собой, но противоположны по знаку. Для получения уравнения с одним неизвестным уравнения системы почленно складываем:
Полученное значение х = 4 подставляем в какое-нибудь уравнение системы, например в первое, и находим значение у: 
2) 
Уравняем коэффициенты при х. Для этого умножим первое уравнение на 3, а второе на (– 2) и сложим полученные уравнения.
Ответ: 
2. Способ подстановки. Из любого уравнения системы одну из неизестных выражаем через остальные, а затем подставляем значение этой неизвестной в остальные уравнения. Рассмотрим этот способ на конкретных примерах:
1) Решим систему уравнений 

Подставим у = 1 в выражение для х, получим 
Ответ: 
2) 



Ответ: 
3) Решим систему уравнений 

Подставим у = 5 в выражение для х, получим
Ответ: 
3. Способ замены. К cистемам двух линейных уравнений с двумя неизвестными можно приводить некоторые нелинейные системы. Это можно осуществлять способом замены.
Пример. Решить систему. 
Перепишем систему в виде: 








Ответ: 
Исследование системы уравнений
Исследуем сколько решений может иметь система уравнений 


А) Если 
Б) Если 
В) Если 
Пример. 

Действительно, 

Ответ: 
Пример. 


Пример. 


Уравнения, содержащие модуль
При решении уравнений, содержащих модуль, используется понятие модуля действительного числа. Модулем (абсолютной величиной) действительного числа а называется само это число, если 


Итак, 




Если D = 0, квадратное уравнение, очевидно, имеет два одинаковых решения (кратных корня).
http://www.evkova.org/sistemyi-linejnyih-uravnenij
http://pandia.ru/text/78/105/1499.php