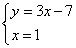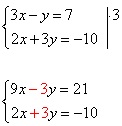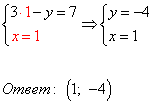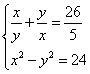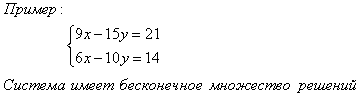Системы уравнений подстановка сложение и графическое

Математика

Тестирование онлайн

Система линейных уравнений

Обычно уравнения системы записывают в столбик одно под другим и объединяют фигурной скобкой

Система уравнений такого вида, где a, b, c — числа, а x, y — переменные, называется системой линейных уравнений.

При решении системы уравнений используют свойства, справедливые для решения уравнений.

Решение системы линейных уравнений способом подстановки

Рассмотрим пример

1) Выразить в одном из уравнений переменную. Например, выразим y в первом уравнении, получим систему:

2) Подставляем во второе уравнение системы вместо y выражение 3х-7:

3) Решаем полученное второе уравнение:

4) Полученное решение подставляем в первое уравнение системы:

Система уравнений имеет единственное решение: пару чисел x=1, y=-4. Ответ: (1; -4), записывается в скобках, на первой позиции значение x, на второй — y.

Решение системы линейных уравнений способом сложения

Решим систему уравнений из предыдущего примера методом сложения.

1) Преобразовать систему таким образом, чтобы коэффициенты при одной из переменных стали противоположными. Умножим первое уравнение системы на «3».

2) Складываем почленно уравнения системы. Второе уравнение системы (любое) переписываем без изменений.

3) Полученное решение подставляем в первое уравнение системы:

Решение системы линейных уравнений графическим способом

Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.

Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может: а) иметь единственное решение; б) не иметь решений; в) иметь бесконечное множество решений.

2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.

Графическое решение системы

Метод введения новых переменных

Замена переменных может привести к решению более простой системы уравнений, чем исходная.

Рассмотрим решение системы

Введем замену 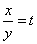, тогда

Переходим к первоначальным переменным

Особые случаи

Не решая системы линейных уравнений, можно определить число ее решений по коэффициентам при соответствующих переменных.

Пусть дана система

1) Если 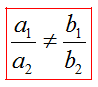, то система имеет единственное решение.

2) Если , то система решений не имеет. В этом случае прямые, являющиеся графиками уравнений системы, параллельны и не совпадают.

3) Если , то система имеет бесконечное множество решений. В этом случае прямые совпадают друг с другом.

Метод Гаусса*

Суть метода в последовательном исключении неизвестных, приводя систему линейных уравнений к ступенчатой форме.

Методы решения систем уравнений с двумя переменными

п.1. Метод подстановки

Вариант 1
Шаг 1. Из одного уравнения выразить y через x: y(x).
Шаг 2. Подставить полученное выражение во второе уравнение и найти x.
Шаг 3. Подставить найденный x в y(x) и найти y.
Шаг 4. Записать полученные пары решений. Работа завершена.

Вариант 2
Шаг 1. Из одного уравнения выразить x через y: x(y).
Шаг 2. Подставить полученное выражение во второе уравнение и найти y.
Шаг 3. Подставить найденный y в x(y) и найти x.
Шаг 4. Записать полученные пары решений. Работа завершена.

п.2. Метод сложения

п.3. Метод замены переменных

Иногда удобно ввести новые переменные и решить систему для них.
А затем, вернуться к исходным переменным и найти их значения.

п.4. Графический метод

Графический метод подробно рассмотрен в §15 данного справочника.

п.5. Примеры

Пример 1. Решите систему уравнений:
а) \( \left\< \begin < l >\mathrm & \\ \mathrm & \end\right. \)
Решаем методом подстановки: \( \left\< \begin < l >\mathrm & \\ \mathrm & \end\right. \)
Для нижнего уравнения: \( \mathrm \)
Подставляем в верхнее уравнение: \( \mathrm \)

б) \( \left\< \begin < l >\mathrm & \\ \mathrm <(x^2+y^2)xy=10>& \end\right. \)
Замена переменных: \( \left\< \begin < l >\mathrm & \\ \mathrm & \end\right. \)
Выразим (x 2 + y 2 ) через a и b:
x 2 + y 2 = (x 2 + y 2 + 2xy) – 2xy = (x + y) 2 – 2xy = a 2 – 2b
Подставляем: \( \left\< \begin < l >\mathrm & \\ \mathrm <(a^2-2b)b=10>& \end\right.\Rightarrow \left\< \begin < l >\mathrm & \\ \mathrm <9b-2b^2=10>& \end\right. \)
Решаем нижнее уравнение: 2b 2 – 9b + 10 = 0 $$ \mathrm< D=9^2-4\cdot 2\cdot 10=1,\ \ b=\frac<9\pm 1><4>> = \left[\begin < l >\mathrm & \\ \mathrm & \end\right. $$ Возвращаемся к исходным переменным: \( \left[\begin < l >\left\<\begin < l >\mathrm & \\ \mathrm & \end\right.& \\ \left\<\begin < l >\mathrm & \\ \mathrm & \end\right. \end\right. \)

Как решать системы уравнений с двумя переменными

Что такое система уравнений с двумя переменными

Системой уравнений в алгебре называется некое условие, смысл которого заключается в одновременном выполнении нескольких уравнений относительно нескольких (либо одной) переменных.

Это значит, что система представляет собой комплекс уравнений. Данные равенства могут содержать одну, две или более переменных. Основным условием понятия «система уравнений» является то, что все эти уравнения выполняются в одно время.

Объединить уравнения в систему можно с помощью фигурной скобки:

У р а в н е н и е 1 У р а в н е н и е 2 У р а в н е н и е 3 …

Графический метод решения

Принцип решения систем уравнений графическим способом заключается в построении графиков для каждого уравнения в общей системе координат. Тогда решения системы соответствуют точкам, в которых данные графики пересекаются. После объяснения решения ответ принято записывать, как координаты этих точек.

Разберем наглядный пример. Предположим, что дана некая система уравнений, решать которую нужно графическим способом. Выполним работу последовательно:

1. Запишем систему.
2. Выразим одну из переменных (пусть это будет у).
3. Построим на координатной прямой графики функций.
4. Найдем точки пересечения графиков.

2 x + 3 y = 12 3 x — y = 7 ⇔ y = 4 — 2 3 x y = 3 x — 7

Заметим, что точка пересечения графиков имеет следующие координаты:

Графический метод решения систем уравнений уступает в точности другим способам. Использовать график целесообразно в том случае, когда в задаче записана система линейных уравнений. Подобные задачи встречаются в средних классах школы. Такие уравнения имеют вид y = a x + b без квадратных членов, а их графики являются прямыми.

Метод подстановки

Алгоритм решения системы уравнений с помощью метода подстановки:

• выражение одной переменной через другие;
• подстановка выражения, которое получилось, в начальные уравнения на место выраженной переменной;
• повторение второго шага до тех пор, пока не будут определены другие переменные.

Рассмотрим последовательность действий на практике. Предположим, что имеется некая система уравнений, которую требуется решить:

2 x + 3 y = 12 3 x — y = 7

Выразим у из второго уравнения:

Выполним подстановку полученного выражения в первое равенство:

2 x + 3 3 x — 7 = 12

Для полученного уравнения с одной переменной несложно найти корни:

2 x + 3 3 x — 7 = 12

2 x + 3 · 3 x — 3 · 7 = 12

2 x + 9 x — 21 = 12

Зная х, выполним подстановку и найдем у:

y = 3 x — 7 = 3 · 3 — 7 = 2 .

Запишем в ответ значения двух переменных.

Ответ: x = 3 ; y = 2 , либо (3;2).

Метод сложения

При сложении левых частей пары (или более) уравнений выражение, полученное в результате, равно сложенным правым частям этих же равенств, согласно формуле:

a = b c = d ⇒ a + c = b + d

В обратную сторону записанное свойство не работает:

a + c = b + d ◃ ≠ ▹ a = b c = d

Таким образом, при решении систем уравнений можно увеличивать обе части уравнения на одинаковое число. Например, сложим первое уравнение с числом с:

a = b c = d ⇒ a + c = b + c

Исходя из того что c=d, можно выполнить замену c на d справа:

a = b c = d ⇒ a + c = b + c ⇒ a + c = b + d .

В качестве примера попробуем решить систему уравнений:

2 x + y = 12 3 x — y = 3

Следуя правилу, суммируем уравнения. В процессе левые части складываем друг с другом. Аналогичным образом поступим с правыми частями равенств. В результате:

2 x + y = 12 3 x — y = 3 ⇒ 2 x ¯ ¯ + y ¯ + 3 x ¯ ¯ — y ¯ = 15 ⇔ 5 x = 15 ⇔ x = 3 .

Получилось избавиться от переменной у. В итоге задача значительно упростилась. Подставим число 3 на место слагаемого с х:

2 x + y = 12 x = 3 ⇔ 2 · 3 + y = 12 x = 3 ⇔ y = 6 x = 3

В следующем примере система уравнений имеет следующий вид:

2 x + 3 y = 13 4 x + 5 y = 23

Заметим, что с помощью сложения задание не получится упростить. В этом случае можно воспользоваться умножением уравнения на какое-либо число, отличное от нуля. Важно выбрать такой множитель, который позволит избавиться от одной из переменных. В этом случае лучше использовать (-2):

2 x + 3 y = 13 · — 2 4 x + 5 y = 23 ⇔ — 4 x — 6 y = — 26 4 x + 5 y = 23

Приступим к сложению:

— 4 x — 6 y = — 26 4 x + 5 y = 23 ⇒ — 4 x — 6 y + 4 x + 5 y = — 26 + 23 ⇔ — y = — 3 ⇔

Выполним подстановку у=3 в первое уравнение:

2 x + 3 y = 13 y = 3 ⇔ 2 x + 9 = 13 y = 3 ⇔ x = 2 y = 3

Задания для самостоятельного решения

Нужно решить систему уравнений:

13 x + 6 y = 7 2 x — 4 y = 6

Выразим х с помощью второго уравнения:

Найти значения переменных:

2 x + 5 y = 10 8 y — 5 x = 57

Из первого равенства выразим х:

2 x + 5 y = 10 2 x = 10 — 5 y

Подставим полученное значение во второе уравнение и запишем ответ.

Дана система уравнений, которую требуется решить:

2 x + 5 y = 10 3 x — 2 y = 1

В данном случае следует умножить первое уравнение на число 2, а второе равенство умножить на число 5:

2 x + 5 y = 10 · 2 3 x — 2 y = 1 · 5 ⇔ 4 x + 10 y = 20 15 x — 10 y = 5

После сложения уравнений остается лишь определить х:

19 x = 25 ⇔ x = 25 19

При подстановке х в какое-либо из двух уравнений можно вычислить у и записать ответ.

Ответ: ( 25 19 ; 28 19 ) .

Требуется найти переменные:

3 y — 4 x = — 13 3 x + 7 y = 56

Здесь следует в первую очередь найти произведение первого уравнения и числа 3, умножить второе уравнение на множитель 4. Далее остается суммировать уравнения и записать ответ.

Нужно решить систему уравнений:

7 x + 3 y = 21 4 y — 5 x = — 15

Множителем для первого уравнения является число 4. Второе уравнение нужно умножить на -3. Полученные равенства следует сложить и записать ответ.

Решить систему уравнений:

6 x — 8 y = — 2 9 x + 10 y = 8

В данном случае предполагается умножение уравнений на дробные числа. Множителем для первого уравнения является дробь 1 4 . Второе уравнение следует умножить на 1 5 :

6 x — 8 y = — 2 · 1 4 9 x + 10 y = 8 · 1 5 ⇔ 6 4 x — 2 y = — 1 2 9 5 x — 2 y = 8 5

Далее выполним сложение:

6 4 x — 2 y = — 1 2 9 5 x — 2 y = 8 5 ⇔ 3 2 x + 9 5 x =-0,5+1,6 ⇔ ⇔ 15 10 x + 18 10 x = 1,1 ⇔ 33 10 x = 1 , 1 ⇔ ⇔ 33 = 11 x x = 3

Путем подстановки определим y:

6 3 — 8 y = — 2 x = 3 ⇔ — 8 y = — 4 x = 3 ⇔ y = 2 x = 3

Найти корни следующих систем уравнений:

2 x + 3 y = 11 3 x + 2 y = 9

3 x — y = 85 5 x + 2 y = 17

x — 3 y = 6 2 y — 5 x = — 4

y 4 — x 5 = 6 x 15 + y 12 = 0

y — x = 5 x + 3 y = 3

Ответ: (1; 3), (17; -34), (0; -2), (-15; 12), (-3; 2).