Системы уравнений с одной переменной 8 класс

Конспект урока «Понятие решения системы уравнений с одной переменной»
план-конспект урока по алгебре (8 класс) на тему

Цели урока: Развитие личности учащихся на основе усвоения предметных знаний УУД.

– ввести понятие системы неравенств с одной переменной, решения системы неравенств;

– составить алгоритм решения системы неравенств с одной переменной;

– отработать навыки применения данного алгоритма к решению системы неравенств;

— формировать умение решать системы неравенств с помощью геометрической модели числовых промежутков;

– развивать вычислительные навыки;

– развивать математическую речь.

Скачать:

Предварительный просмотр:

Конспект урока по алгебре 8 класс

«Понятие решения системы неравенств с одной переменной»

Цели урока: Развитие личности учащихся на основе усвоения предметных знаний УУД.

– ввести понятие системы неравенств с одной переменной, решения системы неравенств;

– составить алгоритм решения системы неравенств с одной переменной;

– отработать навыки применения данного алгоритма к решению системы неравенств;

— формировать умение решать системы неравенств с помощью геометрической модели числовых промежутков;

– развивать вычислительные навыки;

– развивать математическую речь.

Задачи урока: формирование УУД

Формирование коммуникативных УУД – учить высказывать суждения с использованием математических терминов и понятий таких, как числовые неравенства, свойства числовых неравенства, пересечение и объединение множеств, числовые промежутки; сотрудничать с товарищами при выполнении заданий в паре; сравнивать полученные результаты, выслушивать партнера, корректно сообщать товарищу об ошибках, задавать вопросы с целью получения нужной информации; организовывать взаимопроверку выполненной работы; высказывать свое мнение при обсуждении задания.

Формирование познавательных УУД – предлагать мыслительные операции в ходе поиска решения системы неравенств, применять правила – определение решения системы неравенств, перенос слагаемых, приведение подобных слагаемых, свойства неравенств, изображение решений неравенств на координатной прямой, запись ответа.

Формирование регулятивных действий – научить ученика контролировать, выполнять свои действия по заданному алгоритму, научить контролировать свою речь, помочь адекватно оценивать выполненную работу, проверять результаты вычислений, адекватно воспринимать указания на ошибки и исправлять найденные ошибки, оценивать собственные успехи в вычислительной деятельности.

Тип урока : урок получения новых знаний, изучения нового материала.

Предполагаемые результаты: повышение активности и самостоятельности на уроке.

Формы организации урока: индивидуальная, фронтальная, парная.

Как решать систему уравнений

О чем эта статья:

8 класс, 9 класс, ЕГЭ/ОГЭ

Основные понятия

Алгебра в 8 и 9 классе становится сложнее. Но если изучать темы последовательно и регулярно практиковаться в тетрадке и онлайн — ходить на уроки математики будет не так страшно.

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в исходное уравнение получилось верное числовое равенство.

Например, возьмем 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.

Уравнением можно назвать, например, равенство 3 + x = 7 с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Система уравнений — это несколько уравнений, для которых надо найти значения неизвестных, каждое из которых соответствует данным уравнениям.

Так как существует множество уравнений, составленных с их использованием систем уравнений также много. Поэтому для удобства изучения существуют отдельные группы по схожим характеристикам. Рассмотрим способы решения систем уравнений.

Линейное уравнение с двумя переменными

Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.

Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому уравнению и обращает его в верное числовое равенство.

Теорема, которую нужно запомнить: если в линейном уравнение есть хотя бы один не нулевой коэффициент при переменной — его графиком будет прямая линия.

Вот алгоритм построения графика ax + by + c = 0, где a ≠ 0, b ≠ 0:

Дать переменной 𝑥 конкретное значение x = x₁, и найти значение y = y₁ при ax₁ + by + c = 0.

Дать x другое значение x = x₂, и найти соответствующее значение y = y₂ при ax₂ + by + c = 0.

Построить на координатной плоскости xy точки: (x₁; y₁); (x₂; y₂).

Провести прямую через эти две точки и вуаля — график готов.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Система двух линейных уравнений с двумя переменными

Для ax + by + c = 0 можно сколько угодно раз брать произвольные значение для x и находить значения для y. Решений в таком случае может быть бесчисленное множество.

Система линейных уравнений (ЛУ) с двумя переменными образуется в случае, когда x и y связаны не одним, а двумя уравнениями. Такая система может иметь одно решение или не иметь решений совсем. Выглядит это вот так:

Из первого линейного уравнения a₁x + b₁y + c₁ = 0 можно получить линейную функцию, при условии если b₁ ≠ 0: y = k₁x + m₁. График — прямая линия.

Из второго ЛУ a₂x + b₂y + c₂ = 0 можно получить линейную функцию, если b₂ ≠ 0: y = k₂x + m₂. Графиком снова будет прямая линия.

Можно записать систему иначе:

Множеством решений первого ЛУ является множество точек, лежащих на определенной прямой, аналогично и для второго ЛУ. Если эти прямые пересекаются — у системы есть единственное решение. Это возможно при условии, если k₁ ≠ k₂.

Две прямые могут быть параллельны, а значит, они никогда не пересекутся и система не будет иметь решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ ≠ m₂.

Две прямые могут совпасть, и тогда каждая точка будет решением, а у системы будет бесчисленное множество решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ = m₂.

Метод подстановки

Разберем решение систем уравнений методом подстановки. Вот алгоритм при переменных x и y:

Выразить одну переменную через другую из более простого уравнения системы.

Подставить то, что получилось на место этой переменной в другое уравнение системы.

Решить полученное уравнение, найти одну из переменных.

Подставить поочередно каждый из найденных корней в уравнение, которое получили на первом шаге, и найти второе неизвестное значение.

Записать ответ. Ответ принято записывать в виде пар значений (x; y).

Потренируемся решать системы линейных уравнений методом подстановки.

Пример 1

Решите систему уравнений:

x − y = 4
x + 2y = 10

Выразим x из первого уравнения:

x − y = 4
x = 4 + y

Подставим получившееся выражение во второе уравнение вместо x:

x + 2y = 10
4 + y + 2y = 10

Решим второе уравнение относительно переменной y:

4 + y + 2y = 10
4 + 3y = 10
3y = 10 − 4
3y = 6
y = 6 : 3
y = 2

Полученное значение подставим в первое уравнение вместо y и решим уравнение:

x − y = 4
x − 2 = 4
x = 4 + 2
x = 6

Ответ: (6; 2).

Пример 2

Решите систему линейных уравнений:

x + 5y = 7
3x = 4 + 2y

Сначала выразим переменную x из первого уравнения:

x + 5y = 7
x = 7 − 5y

Выражение 7 − 5y подставим вместо переменной x во второе уравнение:

3x = 4 + 2y
3 (7 − 5y) = 4 + 2y

Решим второе линейное уравнение в системе:

3 (7 − 5y) = 4 + 2y
21 − 15y = 4 + 2y
21 − 15y − 2y = 4
21 − 17y = 4
17y = 21 − 4
17y = 17
y = 17 : 17
y = 1

Подставим значение y в первое уравнение и найдем значение x:

x + 5y = 7
x + 5 = 7
x = 7 − 5
x = 2

Ответ: (2; 1).

Пример 3

Решите систему линейных уравнений:

x − 2y = 3
5x + y = 4

Из первого уравнения выразим x:

x − 2y = 3
x = 3 + 2y

Подставим 3 + 2y во второе уравнение системы и решим его:

5x + y = 4
5 (3 + 2y) + y = 4
15 + 10y + y = 4
15 + 11y = 4
11y = 4 − 15
11y = −11
y = −11 : 11
y = −1

Подставим получившееся значение в первое уравнение и решим его:

x − 2y = 3
x − 2 (−1) = 3
x + 2 = 3
x = 3 − 2
x = 1

Ответ: (1; −1).

Метод сложения

Теперь решим систему уравнений способом сложения. Алгоритм с переменными x и y:

При необходимости умножаем почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами.

Складываем почленно левые и правые части уравнений системы.

Решаем получившееся уравнение с одной переменной.

Находим соответствующие значения второй переменной.

Запишем ответ в в виде пар значений (x; y).

Система линейных уравнений с тремя переменными

Системы ЛУ с тремя переменными решают так же, как и с двумя. В них присутствуют три неизвестных с коэффициентами и свободный член. Выглядит так:

Решений в таком случае может быть бесчисленное множество. Придавая двум переменным различные значения, можно найти третье значение. Ответ принято записывать в виде тройки значений (x; y; z).

Если x, y, z связаны между собой тремя уравнениями, то образуется система трех ЛУ с тремя переменными. Для решения такой системы можно применять метод подстановки и метод сложения.

Решение задач

Разберем примеры решения систем уравнений.

Задание 1. Как привести уравнение к к стандартному виду ах + by + c = 0?

5x − 8y = 4x − 9y + 3

5x − 8y = 4x − 9y + 3

5x − 8y − 4x + 9y = 3

Задание 2. Как решать систему уравнений способом подстановки

Выразить у из первого уравнения:

Подставить полученное выражение во второе уравнение:

Найти соответствующие значения у:

Задание 3. Как решать систему уравнений методом сложения

1. Решение систем линейных уравнений начинается с внимательного просмотра задачи. Заметим, что можно исключить у. Для этого умножим первое уравнение на минус два и сложим со вторым:

1. Решаем полученное квадратное уравнение любым способом. Находим его корни:

1. Найти у, подставив найденное значение в любое уравнение:

1. Ответ: (1; 1), (1; -1).

Задание 4. Решить систему уравнений

Решим второе уравнение и найдем х = 2, х = 5. Подставим значение переменной х в первое уравнение и найдем соответствующее значение у.

Задание 5. Как решить систему уравнений с двумя неизвестными

При у = -2 первое уравнение не имеет решений, при у = 2 получается:

Решение систем неравенств с одной переменной

Понятие системы неравенств с одной переменной и его решения

Несколько неравенств с одной переменной образуют систему , если нужно найти такое множество значений переменной, которое будет решением каждого из неравенств.

Решением системы неравенств с одной переменной является такое множество значений этой переменной, которое превращает каждое из неравенств в верное числовое неравенство.

Следствие: общим решением системы неравенств с одной переменной является пересечение частных решений каждого из неравенств системы .

Например: $<\left\< \begin x+7 \ge 2 \\ x-4 \lt 1 \end \right.> \iff <\left\< \begin x \ge -5 \\ x \lt 5 \end \right.> \iff -5 \le x \lt 5 или x \in \Bbb[-5;5)$ — полуинтервал

Алгоритм решения системы неравенств с одной переменной

Подробно о числовой прямой и видах числовых промежутков на ней рассказано в §16 данного справочника. Здесь мы изобразим числовые промежутки как решения неравенств на более простых примерах.

Шаг 1. Найти множество частных решений для каждого из неравенств системы. Если хотя бы одно из частных решений является пустым множеством, вся система неравенств не имеет решений; перейти к шагу 4.

Шаг 2. Начертить друг под другом числовые прямые, число которых равно числу полученных частных решений. Начала отсчёта числовых прямых должны находиться на общем перпендикуляре, единичный отрезок должен совпадать .

Шаг 3. На числовых прямых изобразить полученные частные решения, на отдельной прямой найти их пересечение – это и будет общим решением системы .

Шаг 4. Работа завершена.

Например: $<\left\< \begin x-2 \lt 1 \\ x+5 \ge 6 \end \right.> \iff <\left\< \begin x \lt 3 \\ x \ge 1 \end \right.> \iff 1 \le x \lt 3 или x \in \Bbb[1;3)$ — полуинтервал

Если в системе неравенств есть несколько неравенств со знаком «больше», то из них останется одно неравенство по принципу «больше большего».

Если в системе неравенств есть несколько неравенств со знаком «меньше», то из них останется одно неравенство по принципу «меньше меньшего» .

1) В системе $ <\left\< \begin x \gt 5 \\ x \gt 2 \\ x \gt 3 \end \right.> $ наибольшее число (условие) справа 5.

По принципу «больше большего» останется: $ <\left\< \begin x \gt 5 \\ x \gt 2 \\ x \gt 3 \end \right.> \iff x \gt 5 $

2) В системе $ <\left\< \begin x \lt 5 \\ x \lt 2 \\ x \lt 3 \end \right.> $ наименьшее число (условие) справа 2.

По принципу «меньше меньшего» останется: $ <\left\< \begin x \lt 5 \\ x \lt 2 \\ x \lt 3 \end \right.> \iff x \lt 2 $

Примеры

Пример 1. Решите системы уравнений:

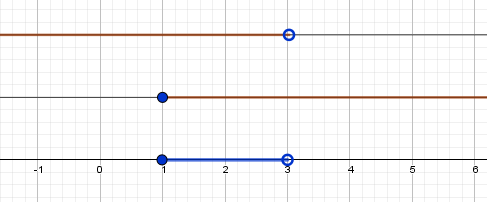
$а) <\left\< \begin 2(x-8) \ge x-16 \\ 3(x+1) \le 11 \end \right.> \iff <\left\< \begin 2x-x \ge -16+16 \\ 2x \le 11-3 \end \right.> \iff <\left\< \begin x \ge 0 \\ 2x \le 8 \end \right.> \iff <\left\< \begin x \ge 0 \\ x \le 4 \end \right.> \iff 0 \le x \le 4$

$x \in [0;4]$ — интервал

$б) <\left\< \begin 5(x-6) \gt x-10 \\ 4(x-1) \lt x+5 \end \right.> \iff <\left\< \begin 5x-x \gt 30-10 \\ 4x-x \lt 5+4 \end \right.> \iff <\left\< \begin 4x \gt 20 \\ 3x \lt 9 \end \right.> \iff <\left\< \begin x \gt 5 \\ x \lt 3 \end \right.> \iff x \in \varnothing$

$x \in \varnothing$ — решений нет

$в) <\left\< \begin -5 \lt 3x+1 \le 4 \\ 3 \lt 2x+5 \lt 9 \end \right.> \iff <\left\< \begin -5-1 \lt 3x \le 4-1 \\ 3-5 \lt 2x \lt 9-5 \end \right.> \iff <\left\< \begin -6 \lt 3x \le 3 \\ -2 \lt 2x \lt 4 \end \right.> \iff <\left\< \begin -2 \lt x \le 1 \\ -1 \lt x \lt 2 \end \right.> \iff$

$$\iff -1 \lt x \le 1$$

$x \in (-1;1] $ — полуинтервал

Пример 2. При каких значениях переменной x имеет смысл выражение:

$ <\left\< \begin x+2 \ge 0 \\ 4-x \ge 0 \end \right.> \iff <\left\< \begin x \ge -2 \\ x \le 4 \end \right.> \iff -2 \le x \le 4 $

$x \in [-1,5;4) \cup (4;+ \infty) $

$ <\left\< \begin x-5 \gt 0 \\ 1-x \gt 0 \end \right.> \iff <\left\< \begin x \gt 5 \\ x \lt 1 \end \right.> \iff x \in \varnothing$

$x \in \varnothing $ — решений нет

Пример 3*. У космического пирата Шутзема несколько затруднительное финансовое положение и только 510 астротугриков в кармане. Однако ему нужно пополнить запасы топлива и продовольствия. Одна капсула с топливом стоит 50 астротугриков, а одна капсула с едой – 30 астротугриков. Какой вариант покупок есть у Шутзема на всю сумму без сдачи, если топлива нужно не менее 4 капсул, а еды – не менее 5?

Пусть x — количество капсул с топливом, y – количество капсул с едой.

По условию задачи:

$$ <\left\< \begin 50x+30y \le 500 \\ x \ge 4 \\ y \ge 5 \\ x,y \in \Bbb N \end \right.> \iff <\left\< \begin 5x+3y \le 50 \\ x \ge 4 \\ y \ge 5 \\ x,y \in \Bbb N \end \right.> $$

Изобразим полученные полуплоскости графически и найдём их пересечение.

Прямая сверху – это бюджетное ограничение.

На этой прямой в области допустимых значений (закрашенный треугольник, стороны включительно) есть только одно целое решение: $ <\left\< \begin x = 6 \\ y = 7 \end \right.> $

Ответ: 6 капсул топлива и 7 капсул еды.