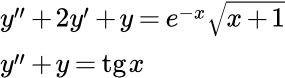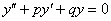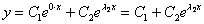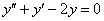Скачать решения дифференциальных уравнений второго порядка

Презентация на тему «Решение Дифференциальных Уравнений второго порядка .»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Описание презентации по отдельным слайдам:

Дифференциальные
уравнения второго порядка

1. Дифференциальные уравнения второго порядка, допускающие его понижение

Дифференциальное уравнение вида:
(1)
где х независимая переменная, у – неизвестная функция и
Общим решением такого уравнения является функция вида:
(2)
где х независимая переменная, у– неизвестная функция и две произвольных постоянные.
Задачей Коши для такого уравнения (1) с начальными условиями
является его решение в виде функции,удовлетворяющей (1), график которой проходит через точку

и имеет тангенс угла наклона касательной в этой точке к оси ОX, равный

ее производные
называется уравнением второго порядка.

Рассмотрим дифференциальные уравнения второго порядка, решение которых сводится к последовательному решению 2х дифференциальных уравнений первого порядка и общий интеграл имеет вид:
где — две произвольных постоянные.
Уравнение с помощью подстановки

cводится к уравнению первого порядка относительно p(x).
Уравнения
не содержат в явной форме искомую функцию и
приводятся подстановкой

к дифференциальным уравнениям первого порядка.
(4)
(3)

Рассмотрим дифференциальные уравнения второго порядка, решение которых сводится к последовательному решению 2х дифференциальных уравнений первого порядка и общий интеграл имеет вид:
где — две произвольных постоянные.

Уравнение
не содержит в явной форме переменную х и приводится подстановкой

к дифференциальным уравнениям первого порядка.
(7)
(3)

Пример 1 .
Решить дифференциальное уравнение
Решение (8).
Это уравнение не содержит явно функцию у . Сделаем замену (6) и получим:

Уравнение второго порядка перешло в линейное уравнение первого порядка, которое можно решить путем замены z = uv. Подставляем это выражение в (8) и получаем:
Приравниваем выражение в скобках к нулю:
и находим v:

Пример 1 .
Решить дифференциальное уравнение
Решение (8).
Подставляем это выражение в (10) и находим u:

2. Дифференциальные уравнения второго порядка с постоянными коэффициентами.

Линейное дифференциальное уравнение второго порядка с постоянными коэффициентами – уравнение вида:

(1)
где a,b,c – заданные действительные числа.
Если функция то уравнение (1) называется ОДНОРОДНЫМ,
если то уравнение (1) называется НЕОДНОРОДНЫМ
Общее решение у неоднородного уравнения складывается из общего решения У соответствующего однородного уравнения и некоторого
частного решения неоднородного дифференциального уравнения:
y = Y+ (2)
Для решения однородного уравнения составляют его характеристическое уравнение: (3)

В зависимости от корней характеристического уравнения общее решение Y находится по одной из формул, представленных в таблице:

Вид частного решения зависит от функции и корней характеристического уравнения.

Пример 1 .
Решить дифференциальное уравнение
Решение
Характеристическое уравнение данного дифференциального уравнения имеет вид (смотрите таблицу):

Легко увидеть, что корнями этого уравнения являются:

Следовательно, общее решение дифференциального уравнения имеет вид (смотрите таблицу):

Пример 2 .
Решить дифференциальное уравнение
Решение
Характеристическое уравнение данного дифференциального уравнения имеет вид (смотрите таблицу):

Легко увидеть, что корнями этого уравнения является кратный корень

Следовательно, общее решение дифференциального уравнения имеет вид (смотрите таблицу):

Система дифференциальных уравнений.

Системой дифференциальных уравнений называется совокупность уравнений, содержащих несколько неизвестных функций и их производные, причем в каждом уравнении имеется хотя бы одна производная.
Система называется линейной, если неизвестные функций и их производные входят в каждое из уравнений только в первой степени.
Линейная система имеет нормальный вид, если она решена относительно всех производных.
Так,например, система дифференциальных уравнений
— линейная и имеет
нормальный вид.
(*)

Система (*) является линейной системой с постоянными коэффициентами (коэффициенты при неизвестных функциях и их производных постоянны).
Решение.
Чтобы исключить y продифференцируем верхнее уравнение системы:

В верхнем уравнении системы находим у:

Подставляя (***) в нижнее уравнение системы, найдем
:

Решение.
Подставляя (****) в (**), получим линейное уравнение второго порядка:

Находим общее решение (*****):

Найденное в п.5 решение подставляем в верхнее уравнение системы и находим вторую неизвестную функцию:
:

В основе методов численного решения дифференциальных уравнений лежит преобразование дифференциальной задачи в разностную задачу, называемое аппроксимацией.
Чтобы лучше понять решение этой задачи в приложении к дифференциальным уравнениям, рассмотрим аппроксимацию простейших дифференциальных операторов, т.е. производных первого и второго порядков.
Рассмотрим функцию одной переменной u = u(x), для которой задан интервал её изменения x [a; b]. Разобьём интервал [a; b] на n равных частей (см. рисунок).
Введём следующие обозначения: u(xj) = uj — значение функции u(x) в точке xj; — величина интервала между точками.

Рассмотрим производную функции u в точке xj:
Аппроксимация этой производной может быть введена с помощью следующих разностных операторов:
с помощью правой конечной разности
с помощью левой конечной разности
с помощью центральной конечной разности

Кроме того, разностную аппроксимацию производной первого порядка можно задать в виде линейной комбинации этих выражений:

Видно, что при = 0 выражение (*) становится левой

конечной разностью, при = 1/2 — центральной конечной

разностью, при = 1 — правой конечной разностью.

Теперь рассмотрим дифференциальное уравнение вида:

Здесь u — функция двух независимых переменных: для которых

задан интервал их изменения:
Введём двумерную систему координат, отложив по оси абсцисс независимую переменную х, а по оси ординат — независимую переменную t, и отметим на осях заданные интервалы изменения переменных х и t. Разобьём интервал [a; b] на некоторое количество равных частей и проведём из каждой точки деления прямую, перпендикулярную оси х.

Выполним те же действия для интервала изменения другой независимой переменной. Тогда построенные прямые составят так называемую разностную сетку (см. рисунок). Точки пересечения проведённых прямых будем называть узлами разностной сетки, причём каждый из них будет соответствовать некоторым значениям независимых переменных х и t из заданных интервалов.
Введём следующие обозначения: j — порядковый номер точки деления по оси х;
n — порядковый номер точки деления по оси t;
— величина интервала между точками по оси х;

величина интервала между точками по оси t;
— значение функции u, соответствующее точкам tn, xj .
Введём нумерацию точек разностной сетки по каждой из осей следующим образом: по оси х — j = 1, 2, 3, . N; по оси t — n = 0, 1, 2, . M.
Рассмотрим производные в уравнении (**) в точке на разностной сетке.
Для аппроксимации производной функции u по времени будем использовать правую конечную разность, стабилизируя при этом значение независимой переменной х в точке с порядковым номером j:

Для аппроксимации второй производной функции u по координате будем использовать другой разностный оператор, стабилизируя при этом значение независимой переменной t в точке с порядковым номером n (или, иначе говоря, на n-ом шаге):
Если подставить записанные конечные разности в исходное дифференциальное уравнение (**), получим соотношение, аппроксимирующее это дифференциальное уравнение в точке на разностной сетке, и называемое разностной схемой:
(***)

В записанной разностной схеме (***) аппроксимация второй производной функции u по координате рассматривается на n-ом шаге по времени, то есть относительно точки tn , для которой рассматривается аппроксимация всего уравнения. Такая разностная схема называется явной.
Однако аппроксимацию второй производной функции u по координате можно рассматривать и на (n + 1)-ом шаге по времени, в точке tn+1; такая разностная схема называется неявной:
Отметим, что если в состав свободного члена входит сама функция u, то её значение должно соответствовать n-му шагу по времени при составлении явной разностной схемы и (n + 1)-му шагу по времени при составлении неявной разностной схемы. Значение же переменной t, входящей в состав свободного члена, всегда берётся на n-ом шаге.
Схематическое изображение узлов разностной сетки, связанных уравнением разностной схемы, называют разностным шаблоном. Разностный шаблон может служить хорошим ориентиром при выборе метода решения разностной схемы и составлении алгоритма решения.
(****)

Схематическое изображение узлов разностной сетки, связанных уравнением разностной схемы, называют разностным шаблоном. Разностный шаблон может служить хорошим ориентиром при выборе метода решения разностной схемы и составлении алгоритма решения.

Разностные шаблоны для разностных схем (***) и (****) имеют вид:

для явной разностной схемы для неявной разностной схемы

Примеры решений дифференциальных уравнений второго порядка методом Лагранжа

Здесь мы применим метод вариации постоянных Лагранжа для решения линейных неоднородных дифференциальных уравнений второго порядка. Подробное описание этого метода для решения уравнений произвольного порядка изложено на странице
Решение линейных неоднородных дифференциальных уравнений высших порядков методом Лагранжа >>> .

Пример 1

Решить дифференциальное уравнение второго порядка с постоянными коэффициентами методом вариации постоянных Лагранжа:
(1)

Шаг 1. Решение однородного уравнения

Вначале мы решаем однородное дифференциальное уравнение:
(2)
Ищем решение в виде . Составляем характеристическое уравнение:

Это уравнение второго порядка.

Решаем квадратное уравнение:
.
Корни кратные: . Фундаментальная система решений уравнения (2) имеет вид:
(3) .
Отсюда получаем общее решение однородного уравнения (2):
(4) .

Шаг 2. Вариация постоянных – замена постоянных функциями

Варьируем постоянные C ₁ и C ₂ . То есть заменим в (4) постоянные и на функции:
.
Ищем решение исходного уравнения (1) в виде:
(5) .

Находим вторую производную:
.
Подставляем в исходное уравнение (1):
(1) ;

.
Поскольку и удовлетворяют однородному уравнению (2), то сумма членов в каждом столбце последних трех строк дает нуль и предыдущее уравнение приобретает вид:
(7) .
Здесь .

Вместе с уравнением (6) мы получаем систему уравнений для определения функций и :
(6) :
(7) .

Решение системы уравнений

Решаем систему уравнений (6-7). Выпишем выражения для функций и :
.
Находим их производные:
;
.

Решаем систему уравнений (6-7) методом Крамера. Вычисляем определитель матрицы системы:

.
По формулам Крамера находим:
;
.

Итак, мы нашли производные функций:
;
.
Интегрируем (см. Методы интегрирования корней). Делаем подстановку
; ; ; .

Общее решение исходного уравнения:

;
.

Пример 2

Решить дифференциальное уравнение методом вариации постоянных Лагранжа:
(8)

Шаг 1. Решение однородного уравнения

Решаем однородное дифференциальное уравнение:

(9)
Ищем решение в виде . Составляем характеристическое уравнение:

Это уравнение имеет комплексные корни:
.
Фундаментальная система решений, соответствующая этим корням, имеет вид:
(10) .
Общее решение однородного уравнения (9):
(11) .

Шаг 2. Вариация постоянных – замена постоянных функциями

Теперь варьируем постоянные C ₁ и C ₂ . То есть заменим в (11) постоянные на функции:
.
Ищем решение исходного уравнения (8) в виде:
(12) .

Далее ход решения получается таким же, как в примере 1. Мы приходим к следующей системе уравнений для определения функций и :
(13) :
(14) .
Здесь .

Решение системы уравнений

Решаем эту систему. Выпишем выражения функций и :
.
Из таблицы производных находим:
;
.

Решаем систему уравнений (13-14) методом Крамера. Определитель матрицы системы:

.
По формулам Крамера находим:
;
.

Первый интеграл немного сложней (см. Интегрирование тригонометрических рациональных функций). Делаем подстановку :

.
Поскольку , то знак модуля под знаком логарифма можно опустить. Умножим числитель и знаменатель на :
.
Тогда
.

Общее решение исходного уравнения:

.

Автор: Олег Одинцов . Опубликовано: 05-08-2013 Изменено: 19-06-2017

823, 26.03.2020 «Решение дифференциальных уравнений 2-го порядка».

Изучить материал, составить конспект, выполнить задание, фото выполненной работы прислать в ВК.

Просмотр содержимого документа
«823, 26.03.2020 «Решение дифференциальных уравнений 2-го порядка».»

Практическая работа по теме: «Решение дифференциальных уравнений II-го порядка»

Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами

В теории и практике различают два типа таких уравнений – однородное уравнение и неоднородное уравнение.

Однородное ДУ второго порядка с постоянными коэффициентами имеет следующий вид:

, где и – константы (числа), а в правой части – строго ноль.

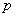
Неоднородное ДУ второго порядка с постоянными коэффициентами имеет вид:
, где и – константы, а – функция, зависящая только от «икс». В простейшем случае функция может быть числом, отличным от нуля.

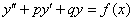
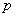
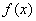
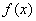
Какая мысль приходит в голову после беглого взгляда? Неоднородное уравнение кажется сложнее. На этот раз первое впечатление не подводит!

Кроме того, чтобы научиться решать неоднородные уравнения необходимо уметь решать однородные уравнения. По этой причине сначала рассмотрим алгоритм решения линейного однородного уравнения второго порядка:

Для того чтобы решить данное ДУ, нужно составить так называемое характеристическое уравнение:

По какому принципу составлено характеристическое уравнение, отчётливо видно:
вместо второй производной записываем ;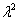
вместо первой производной записываем просто «лямбду»;
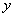
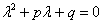
вместо функции ничего не записываем.

– это обычное квадратное уравнение, которое предстоит решить.

Существуют три варианта развития событий.
Они доказаны в курсе математического анализа, и на практике мы будет использовать готовые формулы.

Характеристическое уравнение имеет два различных действительных корня

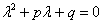
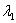
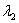
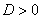
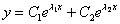
Если характеристическое уравнение имеет два различных действительных корня , (т.е., если дискриминант ), то общее решение однородного уравнения выглядит так:
, где – константы.

В случае если один из корней равен нулю, решение очевидным образом упрощается; пусть, например, 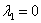, тогда общее решение:

Решить дифференциальное уравнение

Решение: составим и решим характеристическое уравнение:

,

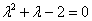
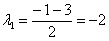
Ответ: общее решение:

Характеристическое уравнение имеет два кратных действительных корня

Если характеристическое уравнение 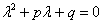имеет два кратных (совпавших) действительных корня (дискриминант ), то общее решение однородного уравнения принимает вид:
, где – константы.
Вместо в формуле можно было нарисовать , корни всё равно одинаковы.

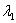
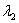
Если оба корня равны нулю , то общее решение опять же упрощается: . Кстати, является общим решением того самого примитивного уравнения , о котором я упоминал в начале урока. Почему? Составим характеристическое уравнение: – действительно, данное уравнение как раз и имеет совпавшие нулевые корни .

Решить дифференциальное уравнение

Решение: составим и решим характеристическое уравнение:

Здесь можно вычислить дискриминант, получить ноль и найти кратные корни. Но можно невозбранно применить известную школьную формулу сокращенного умножения:

Получены два кратных действительных корня

Ответ: общее решение:

Характеристическое уравнение имеет сопряженные комплексные корни

Если характеристическое уравнение 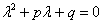имеет сопряженные комплексные корни , (дискриминант ), то общее решение однородного уравнения принимает вид:
, где – константы.
Примечание: Сопряженные комплексные корни почти всегда записывают кратко следующим образом:

Если получаются чисто мнимые сопряженные комплексные корни: , то общее решение упрощается:

Решить однородное дифференциальное уравнение второго порядка

Решение: Составим и решим характеристическое уравнение:

– получены сопряженные комплексные корни

Ответ: общее решение:

Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям ,

Решение: составим и решим характеристическое уравнение:

,
Получены два различных действительных корня, поэтому общее решение:

Алгоритм нахождения частного решения следующий:

Сначала используем начальное условие :

Согласно начальному условию, получаем первое уравнение: или просто

Далее берём наше общее решение и находим производную:

Используем второе начальное условие :

Согласно второму начальному условию, получаем второе уравнение: или просто

Составим и решим систему из двух найденных уравнений:

Подставим найденные значения констант в общее решение :

Ответ: частное решение:

Найти общее решение дифференциального уравнения 2-го порядка.

Найти частное решение дифференциального уравнения 2-го порядка.