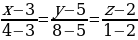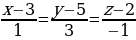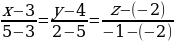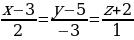Скачать уравнение прямой и плоскости

Уравнения сферы, плоскости и прямой
презентация к уроку по геометрии (10, 11 класс)

Уравнения сферы, плоскости и прямой

Скачать:

Предварительный просмотр:

Подписи к слайдам:

Понятие сферы и её элементов Уравнение сферы в заданной системе координат СФЕРА УРАВНЕНИЕ СФЕРЫ

Тело вращения — сфера

Определение сферы Элементы сферы Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки. т.О — центр сферы ОА – радиус сферы. Любой отрезок, соединяющий центр и какую-нибудь точку сферы называется радиусом сферы. ВС – диаметр сферы. Отрезок, соединяющий две точки сферы и проходящий через ее центр, называется диаметром сферы d=2r

? Какие из тел, изображенных на рисунках, являются сферой? 1 2 3 4 5 6

На плоскости В пространстве L М(х;у) х у L Сформулируйте определение линии L на плоскости Уравнение с двумя переменными х и у называется уравнением линии L , если этому уравнению удовлетворяют координаты любой точки линии L и не удовлетворяют координаты никакой точки, не лежащей на этой линии Уравнение с тремя переменными х,у, z называется уравнением поверхности, если этому уравнению удовлетворяют координаты любой точки поверхности и не удовлетворяют координаты никакой точки, не лежащей на этой поверхности Х z Сформулируйте определение уравнения поверхности в пространстве Х у М(х;у; z ) •

На плоскости В пространстве М(х;у) х у х у z (х;у; z ) С

Частные случаи 1.Уравнение окружности с центром в т.О(0;0) и радиусом r 1.Уравнение сферы с центром в т.О(0;0;0) и радиусом R

Выбрать из предложенных уравнений – уравнение сферы: 1. 2. 3. 4. 5. 6. 7. 8. 1.Ур-е окружности 2.Ур-е сферы 3.Ур-е прямой 4.Ур-е сферы 5.Ур-е параболы 6.Ур-е сферы 7.Ур-е сферы 8. ?

В данных уравнениях определите координаты центра сферы и радиус 1. 2. 3. 4.

Составьте уравнение сферы по следующим данным центра и радиуса сферы: Дано: С(-2;8;1); R =11 Дано: А(3;-2;0); R =0,7 Дано: О(0;0;0); R =1 Проверяем ответы:

Задача Определить принадлежит ли т.А сфере, заданной уравнением если: а) т.А(5;-2;6) б) т.А(-5;2;6) Решение: Равенство верное , следовательно А(5;-2;6) принадлежит сфере Равенство неверное , следовательно А(5;-2;6) не принадлежит сфере

Уравнение плоскости и прямой

совпадают, если существует такое число k , что параллельны, если существует такое число k , что В остальных случаях плоскости пересекаются.

Если известна какая-нибудь точка плоскости M 0 и какой-нибудь вектор нормали к ней , то через заданную точку можно провести единственную плоскость, перпендикулярную данному вектору. Общее уравнение плоскости будет иметь вид: n (A;B;C) M 0

Чтобы получить уравнение плоскости , имеющее приведённый вид, возьмём на плоскости произвольную точку M( x ; y ; z ) . Эта точка принадлежит плоскости только в том случае, когда вектор перпендикулярен вектору (рис), а для этого, необходимо и достаточно, чтобы скалярное произведение этих векторов было равно нулю, т.е. Вектор задан по условию. Координаты вектора найдём по формуле : Теперь, используя формулу скалярного произведения векторов , выразим скалярное произведение в координатной форме:

Используем формулу A ( x — x 0 )+B(y-y 0 )+C(z-z 0 )=0

Уравнение прямой в пространстве Поскольку прямую в пространстве можно рассматривать как линию пересечения двух плоскостей, то одним из способов аналитического задания прямой в пространстве является задание с помощью системы из двух уравнений задающих пару пересекающихся плоскостей.

Уравнение прямой в пространстве Прямую, проходящую через точку A 0 ( x 0 , y 0 , z 0 ) с направляющим вектором ( a , b , c ) можно задавать параметрическими уравнениями В случае, если прямая в пространстве задается двумя точками A 1 ( x 1 , y 1 , z 1 ), A 2 ( x 2 , y 2 , z 2 ), то, выбирая в качестве направляющего векто­ра вектор ( x 2 — x 1 , y 2 — y 1 , z 2 — z 1 ) и в качестве точки А 0 точку А 1 , получим следующие уравнения

Упражнение 1 Какими уравнениями задаются координатные прямые? Ответ: Ось Ox Ось O y Ось O z

Упражнение 2 Напишите параметрические уравнения прямой, проходящей через точку А (1,-2,3) с направляющим вектором, имеющим координаты (2,3,-1). Ответ:

Упражнение 3 Напишите параметрические уравнения прямой, проходящей через точки А 1 (-2,1,-3), А 2 (5,4,6). Ответ:

Упражнение 4 Напишите параметрические уравнения прямой, проходящей через точку M (1,2,-3) и перпендикулярную плоскости x + y + z + 1 = 0. Ответ:

Упражнение 5 В каком случае параметрические уравнения определяют перпендикулярные прямые? Ответ: Если выполняется равенство a 1 a 2 +b 1 b 2 +c 1 c 2 = 0 .

По теме: методические разработки, презентации и конспекты

Практическая работа «Построение углов между плоскостями, между прямой и плоскостью»

Практическая работа по геометрии ,10 класс. Хотя данную работу можно провести при подготовке к ЕГЭ по математике, при решении задач типа С2. Работа содержит 8 заданий на построение угла между прямой и.

Тест по теме «Параллельность прямых и плоскостей. Перпендикулярность прямых в пространстве» (геометрия 10 класс)

Данный тест можно предложить учащимся как входной перед изучением темы «Многогранники».

Параллельность прямых и плоскостей. Параллельные прямые в пространстве

Урок-презентация по геометрии 10 класс.

Тесты по теме «Прямые в пространстве. Параллельность прямых, прямой и плоскости», «Перпендикулярность прямых, прямой и плоскости»

Тесты предназначены для проверки усвоенияследующих понятий и определений: взаимное расположение прямых в пространстве, определение скрещивающихся прямых, определение параллельных прямых, признак парал.

Расстояние от точки до плоскости, от прямой до плоскости, расстояние между плоскостями, между скрещивающимися прямыми, между произвольными фигурами в пространстве

Материал для практической работы «Расстояние от точки до плоскости, от прямой до плоскости, расстояние между плоскостями, между скрещивающимися прямыми, между произвольными фигурами в пространств.

Расстояние от точки до плоскости, от прямой до плоскости

Материал для практической работы «Расстояние от точки до плоскости, от прямой до плоскости&quot.

Составление уравнений сферы, плоскости, прямой.

Составление уравнений сферы, плоскости, прямой.

Уравнение прямой, плоскости и сферы

306 гр. Математика. Дистанционное обучение. Тема 1-3.

Просмотр содержимого документа
«Уравнение прямой, плоскости и сферы»

Тема 1: Уравнение прямой в пространстве.

З адание: записать конспект и выполнить самостоятельную работу.

Пример 1. Составить уравнение прямой, проходящей через две точки:

Подставив в уравнение прямой соответствующие координаты, получим:

Упростим:

Ответ:

Пример 2. Составить уравнение прямой, проходящей через две точки:

Подставив в уравнение прямой соответствующие координаты, получим:

Упростим:

Ответ: 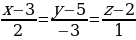Самостоятельная работа

Пример 1. Составить уравнение прямой, проходящей через две точки:

Пример 2. Составить уравнение прямой, проходящей через две точки:

Пример 3. Составить уравнение прямой, проходящей через две точки:

Тема 2: Уравнение плоскости в пространстве

Задание: записать конспект и выполнить самостоятельную работу

П 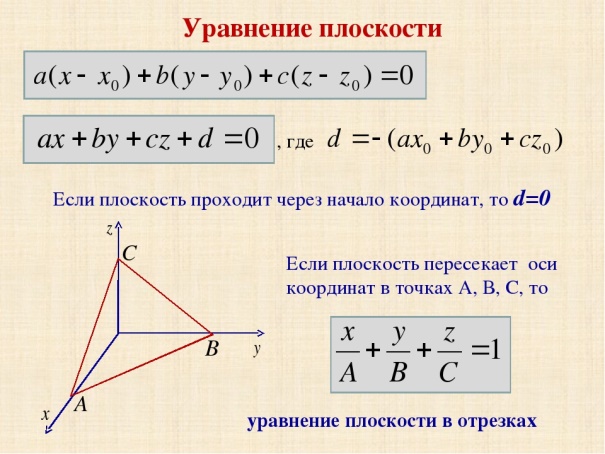ример 1: Принадлежит, ли точка В (-1; 2; 7) плоскости, заданной уравнением 2х+3у-z+3=0

Решение: Подставим координаты точки в уравнение и проверим верно ли равенство.

Ответ: точка В (-1; 2; 7) принадлежит плоскости.

Пример 2: Принадлежит, ли точка Е(0; 4; -6) плоскости, заданной уравнением х-5у-4z+2=0

Решение: Подставим координаты точки в уравнение и проверим верно ли равенство. х-5у-4z+2=0

0-5·4-4·(-6)+2=0-20+24+2=6≠0 не верно

Ответ: точка Е(0; 4; -6) не принадлежит плоскости.

Пример 3: При каком D точка А(1; 5;-2) принадлежит плоскости -3х+2у-z+D=0

Решение: Подставим координаты точки в уравнение и найдем D.

Пример 1: Принадлежит, ли точка В (-2; 3; 8) плоскости, заданной уравнением

Пример 2: Принадлежит, ли точка Е(3; 4; -2) плоскости, заданной уравнением

Пример 3: При каком D точка А(2; 4;-1) принадлежит плоскости -2х+5у-z+D=0

Решить задания №1, №2

О пределение. Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии R от данной точки О.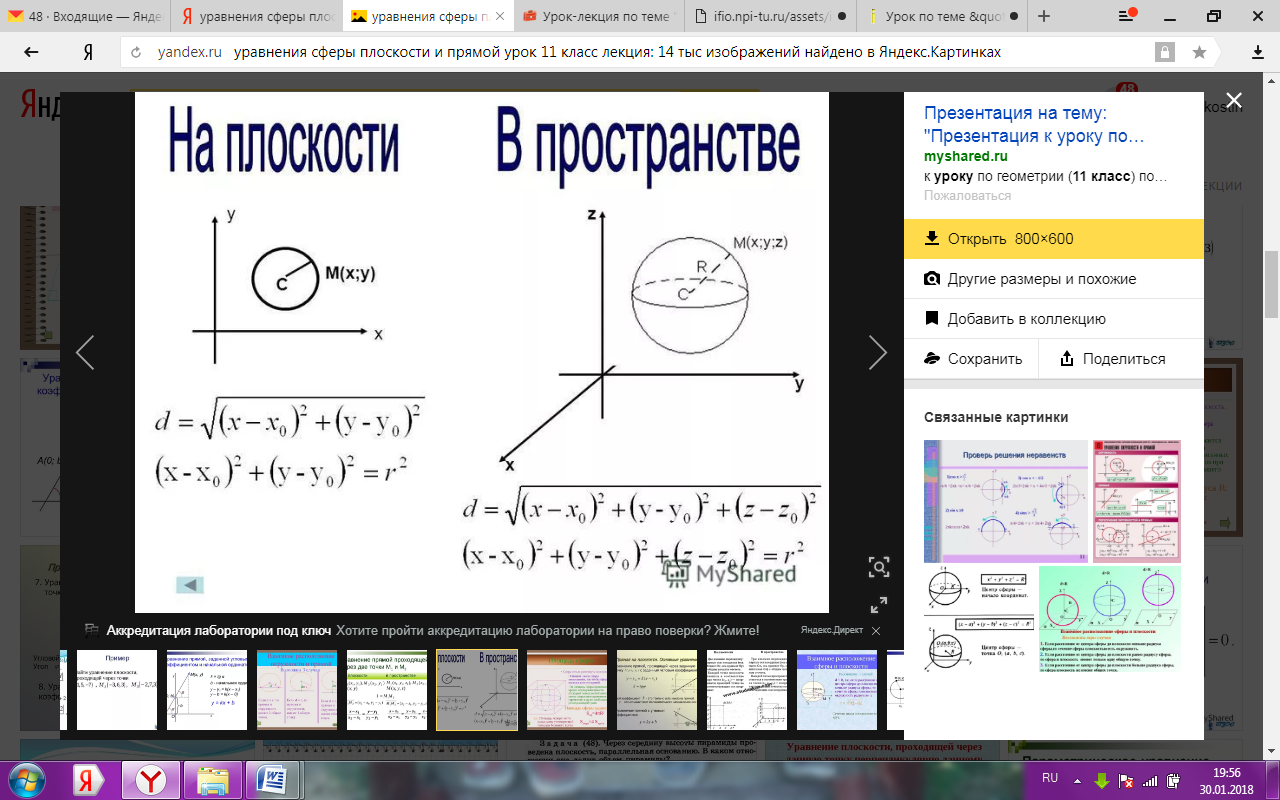

R – радиус сферы, т. О – центр сферы.

Написать уравнение сферы с центром в точке О(1; 2; -5) и радиусом R=3.

Подставим в уравнение сферы: (х-1) 2 +(у-2) 2 +(z-(-5)) 2 =3 2 .

Упростим: (х-1) 2 +(у-2) 2 +(z+5) 2 =9.

Ответ: (х-1) 2 +(у-2) 2 +(z+5) 2 =9.

Пример 2. Дано уравнение сферы: (х-6) 2 +(у+3) 2 +(z-4) 2 =64. Найти координаты центра и радиус сферы.

1)найдем координаты центра: (х-6) 2 +(у-(-3)) 2 +(z-4) 2 =64

2)найдем радиус: R 2 =64, R=√64=8,

Ответ: О(6, -3, 4), R = 8.

Задание 1. Написать уравнение сферы с центром в точке О(5; -2; 3) и радиусом R= 6

Задание 2. Дано уравнение сферы (х-3) 2 +(у+7) 2 +(z-8) 2 =25. Найти координаты центра и радиус сферы.

Презентация по математике на тему: «Прямая в пространстве. Взаимное положение прямой и плоскости. Уравнение прямой на плоскости»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Описание презентации по отдельным слайдам:

Прямая в пространстве Взаимное положение прямой и плоскости Уравнение прямой на плоскости

Прямая в пространстве Уравнение прямой, проходящей через точку в данном направлении Пусть точка принадлежит прямой , а направление совпадает с вектором . Возьмем произвольную точку . Тогда и по свойствам векторов , где – параметр. Равенство – векторное уравнение прямой. Представим его в координатной форме: – параметрическое уравнение прямой. Выразим . Тогда , приравняем эти выражения, получим каноническое уравнение прямой:

Уравнение прямой , проходящей через две точки Пусть точки и , которые принадлежат прямой . Примем вектор за , направляющий вектор, а точку за точку и подставим их в каноническое уравнение прямой. Тогда . Пример: Прямая, проходящая через точку с направляющим вектором . Взаимное расположение двух прямых в пространстве Рассмотрим две прямые , заданные точками и с направляющими векторами . Тогда уравнения этих прямых соответственно

Данные прямые могут быть скрещивающими или лежать на одной плоскости. Рассмотрим векторы . Составим смешанное произведение этих векторов: Тогда, если прямые скрещивающиеся, данные три вектора не могут лежать в одной плоскости, то есть через них нельзя провести плоскость и . Если же прямые лежат в одной плоскости, то есть данные векторы компланарны, то . Во втором случае может быть три случая: Прямые будут параллельны, тогда их направляющие векторы коллинеарны. , по свойствам векторов:

Прямые перпендикулярны, тогда их направляющие векторы перпендикулярны, то по свойствам векторов скалярное произведение равно нулю. Угол между прямыми равен углу между их направляющими векторами, а именно . Прямые будут совпадать, если все три вектор будут коллинеарными, другими словами все три строки определителя будут пропорциональны. Взаимное расположение прямой и плоскости Пусть плоскость задана общим уравнением , прямая параметрическим уравнением: . .

Подставим из уравнения прямой в уравнение плоскости. Тогда Если , то . Подставим полученное значение параметра в уравнение прямой, получим выраженные единственным образом значения , которые определяют координаты единственной точки, являющейся точкой пересечения прямой и плоскости. Таким образом, – условие пересечения прямой и плоскости. Если и , то получаем уравнение – любое число, другими словами имеем бесконечное число решений, то есть бесконечное число точек пересечения прямой плоскости, получается ,что прямая лежит на плоскости. Если и , то , получаем противоречие, следовательно, нет решений и нет общих точек, то есть прямая и плоскость параллельны.

Угол между прямой и плоскостью Пусть плоскость задана общим уравнением , а прямая каноническим уравнением: и пересекает данную плоскость. Возможны два варианта: а) Рис. 1 б) – угол между прямой и плоскостью, – угол между направляющим вектором прямой и нормальным вектором плоскости. Видно, что в случае а) (острый угол), а в случае б) (тупой угол). Объединив, эти формулы получим: .

Прямая на плоскости Общее уравнение прямой Так как мы будем рассматривать прямую на плоскости, то ее можно представить как пересечение плоскости с координатной плоскостью с уравнением z=0, то общее уравнение прямой примет вид: Тогда – общее уравнение прямой на плоскости. Частные случаи общего уравнения прямой , то есть прямая проходит через начало координат. , то есть прямая параллельна оси . , то есть прямая параллельна оси . , то есть прямая совпадает с осью . , то есть прямая совпадает с осью .

Уравнение прямой, проходящей через две точки Пусть и – точки через которые проходит заданная прямая. Вспомним соответствующее уравнение прямой в пространстве: Тогда отбрасывая координаты z, получим , где – направляющий вектор. Уравнение прямой в отрезках Пусть прямая проходит через точки и . Представим, что и подставим в уравнение прямой, проходящей через две точки. Тогда или . Пример: .

Уравнение прямой, проходящей через точку в заданном направлении Пусть направляющий вектор задан, как . Из уравнения прямой, проходящей через две точки получим Таким образом, получили уравнение прямой, проходящей через точку в данном направлении: , где . Уравнение прямой с угловым коэффициентом Пусть прямая проходит через точку , то есть . Тогда, подставив в предыдущее уравнение данные значения, получим , где – начальная ордината. Экономический смысл начальной ординаты: уравнение вида описывает процесс накопления капитала, где – время. Тогда при , получаем что – начальный капитал.

Взаимное расположение двух прямых на плоскости Рассмотрим две прямые и заданные общими уравнениями. По аналогии с плоскостью, прямые параллельны, если их нормальные векторы параллельны. Тогда условие параллельности прямых можно записать как или , так как . Прямые перпендикулярны, если их нормальные векторы перпендикулярны. Условие перпендикулярности можно записать как или . Угол между прямыми равен углу между нормальными векторами, а следовательно Прямые будут совпадать, если

Задания для самостоятельной работы. 1. Ответить на вопросы: Как убедиться, что данная точка лежит на данной линии? Как найти точку пересечения двух линий, заданных своими уравнениями? Что называется порядком алгебраической линии? Как расположена прямая относительно декартовой системы координат, если в ее уравнении отсутствует: а) свободный член; б) одна из координат; в) одна из координат и свободный член? Можно ли найти угловой коэффициент прямой, не составляя ее уравнения, если известны две ее точки? Если да, то как это сделать? Как найти расстояние от данной точки до прямой, заданной уравнением общего вида? Напишите уравнения осей декартовой системы координат. 2. Написать каноническое уравнение прямой 3. Найти точку пересечения прямой и плоскости 4. Даны вершины треугольника АВС: А(1;-1), В(-5; 2) и С(-2; 3). Написать уравнение высоты, опущенной из вершины В. Составить уравнение прямой, проходящей через точку А(1;-1) и образующей с осью Оу угол 60°.

Краткое описание документа:

Данная презентация-сопровождение предназначена для чтения лекций в ВУЗах. Рассчитана на 2-3 академических часа.

В презентациях отображается основной теоретический материал, предлагаются примеры и задания для самостоятельного выполнения.

Создание подобных презентаций дает ряд преимуществ преподавателю при проведении лекций:

1. возможность использования готовых лекций, а также составление своих собственных, путем редактирования или дополнения уже имеющихся;

2. сокращение времени подготовки преподавателя к занятиям;

3. возможность организации дифференцированного подхода к обучению, в том числе и организация обучения студентов, находящихся на индивидуальном обучении (по причине болезни), или при опережающем обучении;

4. презентации помогают углубить восприятие материала и стимулируют мыслительную деятельность учащихся. Сочетание рассказа преподавателя с показом демонстрационного материала способствует развитию аудиовизуальной памяти, а также систематизации знаний. На основе презентаций у студентов формируются и закрепляются умения по составлению опорных схем и конспектов в рабочей тетради;

5. мультимедийное оформление слайдов, композиционный подбор материала способствуют развитию эстетического восприятия учащихся, стимулируют познавательную активность.

6. слайды содержат не только иллюстрации, но и трёхмерные модели, позволяющие студентам познакомиться с понятиями объёмных фигур в пространстве.